6.4.4 练习二十二 课件(共24张PPT)人教版数学六年级下册
文档属性
| 名称 | 6.4.4 练习二十二 课件(共24张PPT)人教版数学六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
第25课时 练习二十二
第六单元 整理和复习
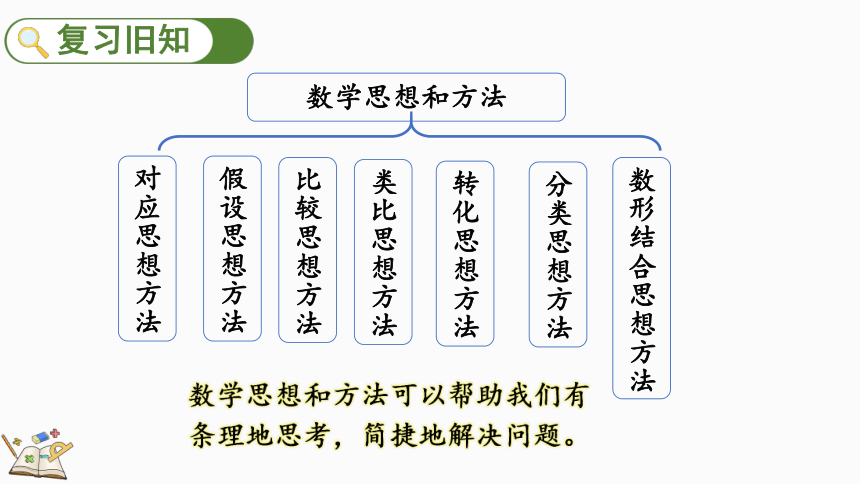
数学思想和方法
对应思想方法
类比思想方法
假设思想方法
比较思想方法
数形结合思想方法
转化思想方法
分类思想方法
数学思想和方法可以帮助我们有条理地思考,简捷地解决问题。
数学思想
利用找规律解决实际问题
根据给定的图形或数字,探索其中简单的排列规律,解决生活中的实际问题。
1.借助图形,用连线的方法,分析。
2.搭配时,有序思考,要有条理,做到不重复、不遗漏。
利用画图解决实际问题
数学思想
生活中的一些推理问题比较复杂,可以借助表格帮助我们推理,从而解决问题。
等量代换是指一个量用与它相等的量去代替,它是数学中一种基本的思想方法。
等量代换
借助列表解决实际问题
找规律,填数。
1
选自教材第102~103页练习二十二
(1) 3,11,20,30, ,53, ,…
(2)1,3,2,6,4,9,8, , ,15, ,18,…
+8
+9
+10
41
65
×2
×2
×2
×2
16
32
+3
+3
+3
12
+3
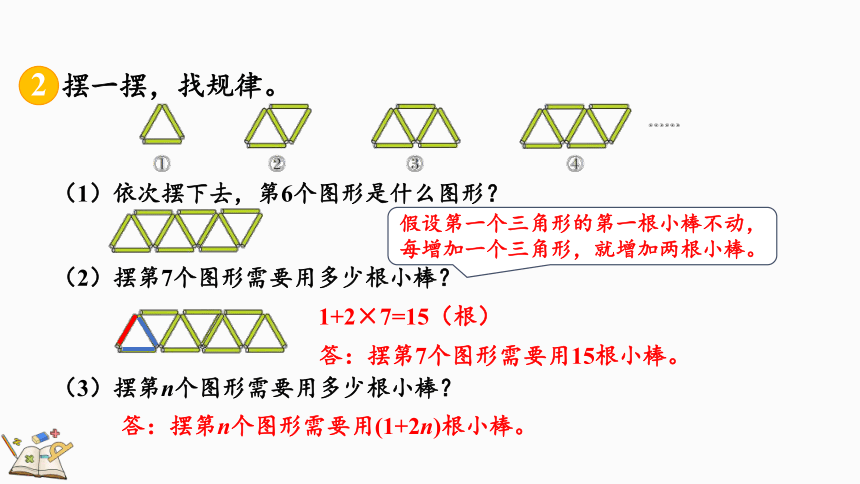
摆一摆,找规律。
2
(1)依次摆下去,第6个图形是什么图形?
(2)摆第7个图形需要用多少根小棒?
(3)摆第n个图形需要用多少根小棒?
假设第一个三角形的第一根小棒不动,每增加一个三角形,就增加两根小棒。
1+2×7=15(根)
答:摆第7个图形需要用15根小棒。
答:摆第n个图形需要用(1+2n)根小棒。
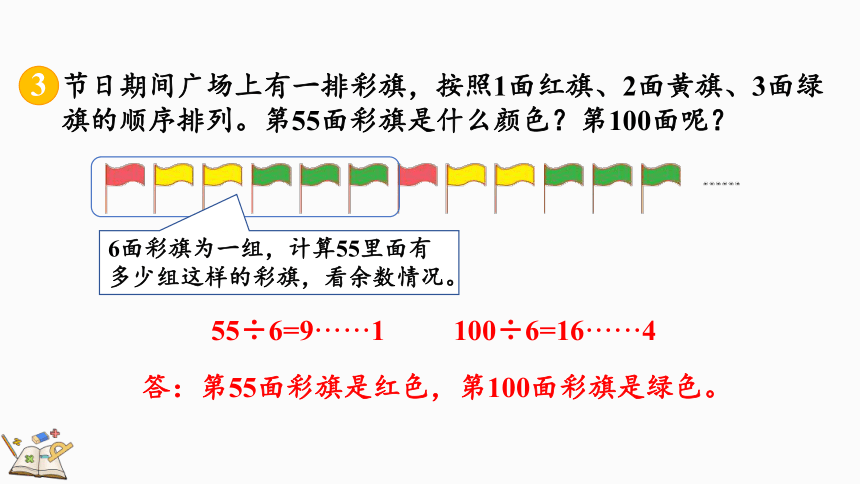
节日期间广场上有一排彩旗,按照1面红旗、2面黄旗、3面绿旗的顺序排列。第55面彩旗是什么颜色?第100面呢?
3
6面彩旗为一组,计算55里面有多少组这样的彩旗,看余数情况。
55÷6=9······1
100÷6=16······4
答:第55面彩旗是红色,第100面彩旗是绿色。
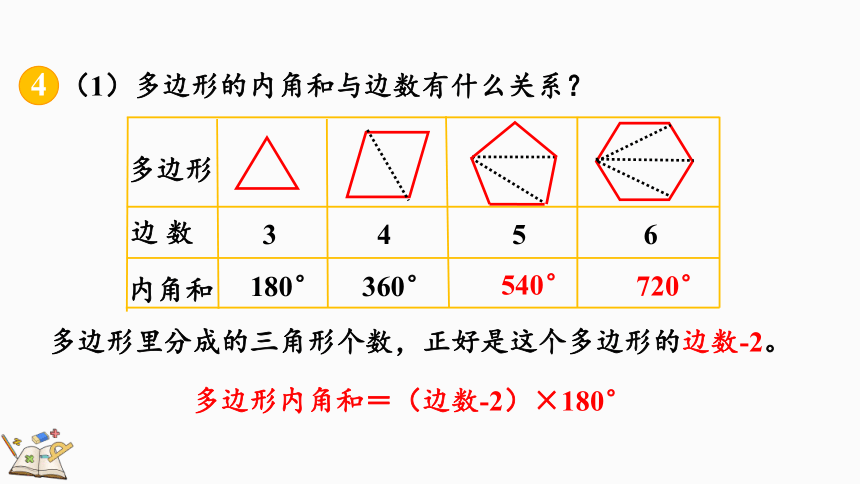
(1)多边形的内角和与边数有什么关系?
4
多边形
边 数
3
4
5
6
内角和
180°
360°
540°
720°
多边形里分成的三角形个数,正好是这个多边形的边数-2。
多边形内角和=(边数-2)×180°
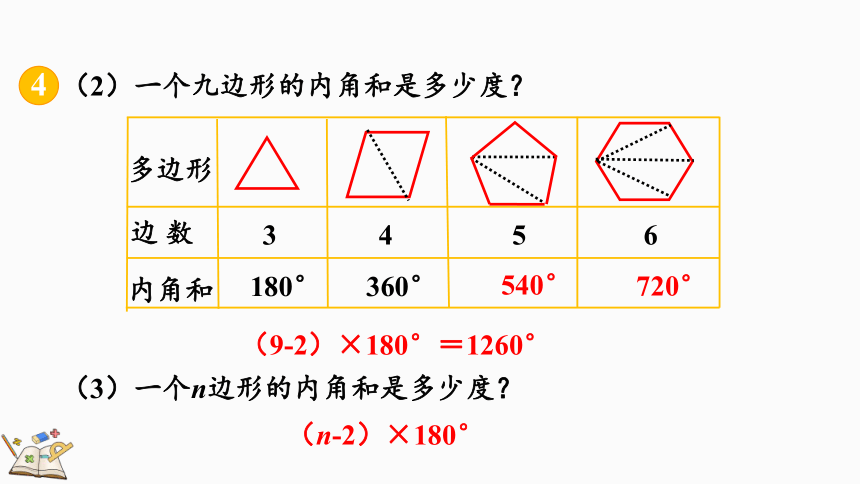
(3)一个n边形的内角和是多少度?
(2)一个九边形的内角和是多少度?
4
多边形
边 数
3
4
5
6
内角和
180°
360°
540°
720°
(9-2)×180°=1260°
(n-2)×180°
小芳、小莉两名女生和小勇、小强两名男生站成一排拍毕业纪念照,如果男女间隔排列,一共有多少种站法?
5
(5)小莉 小勇 小芳 小强
(6)小莉 小强 小芳 小勇
(7)小芳 小勇 小莉 小强
(8)小芳 小强 小莉 小勇
方法一:用列举法
(1)小勇 小莉 小强 小芳
(2)小勇 小芳 小强 小莉
(3)小强 小莉 小勇 小芳
(4)小强 小芳 小勇 小莉
答:共有8种不同的站法。
小勇
小莉
小强
小芳
怎样才能找出所有的排列方法呢?
小芳、小莉两名女生和小勇、小强两名男生站成一排拍毕业纪念照,如果男女间隔排列,一共有多少种站法?
5
小勇
小莉
小强
小芳
怎样才能找出所有的排列方法呢?
方法二:用字母表示法
B1 B2
小勇 小强 小莉 小芳
A1 A2 B1 B2
第一位 第二位 第三位 第四位
A1 A2
答:共有8种不同的站法。
2×4=8
互换
互换
在学校运动会上,1号、2号、3号、4号运动员取得了800 m赛跑的前4名。小记者来采访他们各自的名次。1号说:“3号第一个冲过终点。”另一名运动员说:“2号不是第4名。”小裁判说:“他们的号码与他们的名次都不相同。”他们的名次各是多少?
6
第1名 第2名 第3名 第4名
1号
2号
3号
4号
√
√
×
×
√
√
答:3号第1名,4号第2名,
2号第3名,1号第4名。
警察抓住了4个犯罪嫌疑人,其中的一个人是主谋。甲说:“我不是主谋。”乙说:“丁是主谋。”丙说:“我不是主谋。”丁说:“甲是主谋。”已知他们4个人中只有1个人说了真话。主谋是
谁?
7
需要通过找出题中互相矛盾的条件关系
“甲说自己不是主谋,丙也说自己不是主谋”,从而推知其中两人的话必有真假。
假设甲说的是真话,则说明丙是主谋。
另两个人说的也是假话,与题目都相符。
答:主谋是丙。
○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
8
(1)○+□=91
△+□=63
△+○=46
(2)□-○=8
□+○=12
△=□+□+○
第一个式子减第二个式子得到
○-△=91-63=28
用这个式子加第三个式子得到
○+○=28+46
○=37
第一个式子加第二个式子得到
□+□=8+12=20
○=12-10=2
△=10+10+2=22
□=10
□=91-37=54
△= 46-37=9
如图,把三角形ABC的边BC延长到点D。
(1)∠3和∠4拼成的是什么角?
(2)你能说明∠1+∠2=∠4吗?
9
答:(1)∠3和∠4拼成的是平角。
(2)∠1+∠2+∠3=180°
∠3+∠4=180°
∠1+∠2=∠4
七桥问题
一个城市中有一条河穿过,河中有两个小岛,有七座桥连接其中。有人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥?这就是著名的七桥问题。数学家通过把七桥问题转化成一个几何问题——一笔画问题(如图),发现按上述要求一次走完七座桥的走法是不存在的。
选自教材103页练习二十二“你知道吗?”
选自教材103页练习二十二“你知道吗?”
一笔画问题
通过点的线条数目是双数,称为偶点;通过点的线条数目是单数,称为奇点。
1.图形里如果没有奇点,都可以一笔成的。
2.图形里如果只有一对奇点,那么也可以一笔画画成。
3.图形里的奇点如果是多于一对,就无法一笔画完成。
(奇点的个数为0或2的图形可以一笔画)
1.张老师有50分和80分的邮票各两枚。他用这些邮票能付多少种邮资?
1枚:50分、80分。有2种
2枚:100分、130分、160分。 有3种
3枚:180分、210分。有2种
4枚:260分。有1种
答:他用这些邮票能付8种邮资。
2.学校为艺术节选送节目,从3个合唱节目中选出2个,2个舞蹈节目中选出1个,一共有几种选送方案?
第三步:把两次选法进行搭配,共有6种选法。
第一步:从3个合唱节目中选出2个,有3种选法。
第二步:从2个舞蹈节目中选出1个,有2种选法。
方法一:
答:一共有6种选送方案。
2.学校为艺术节选送节目,从3个合唱节目中选出2个,2个舞蹈节目中选出1个,一共有几种选送方案?
如果用A、B、C表示3个合唱节目,用a、b表示2个舞蹈节目。
a
b
A
B
C
方法二:
答:一共有6种选送方案。
2.学校为艺术节选送节目,从3个合唱节目中选出2个,2个舞蹈节目中选出1个,一共有几种选送方案?
如果用A、B、C表示3个合唱节目,用a、b表示2个舞蹈节目。
方法三:
AB
BC
AC
a
b
答:一共有6种选送方案。
这节课有什么收获呢?
1.会归纳、类比、推理的思想方法,
培养数学的逻辑思维。
2.有序思考解决生活中实际问题。
1.从教材练习二十二中选取;
2.从课时练中选取。
数学思想和方法
对应思想方法
类比思想方法
假设思想方法
比较思想方法
数形结合思想方法
转化思想方法
分类思想方法
第25课时 练习二十二
第六单元 整理和复习
数学思想和方法
对应思想方法
类比思想方法
假设思想方法
比较思想方法
数形结合思想方法
转化思想方法
分类思想方法
数学思想和方法可以帮助我们有条理地思考,简捷地解决问题。
数学思想
利用找规律解决实际问题
根据给定的图形或数字,探索其中简单的排列规律,解决生活中的实际问题。
1.借助图形,用连线的方法,分析。
2.搭配时,有序思考,要有条理,做到不重复、不遗漏。
利用画图解决实际问题
数学思想
生活中的一些推理问题比较复杂,可以借助表格帮助我们推理,从而解决问题。
等量代换是指一个量用与它相等的量去代替,它是数学中一种基本的思想方法。
等量代换
借助列表解决实际问题
找规律,填数。
1
选自教材第102~103页练习二十二
(1) 3,11,20,30, ,53, ,…
(2)1,3,2,6,4,9,8, , ,15, ,18,…
+8
+9
+10
41
65
×2
×2
×2
×2
16
32
+3
+3
+3
12
+3
摆一摆,找规律。
2
(1)依次摆下去,第6个图形是什么图形?
(2)摆第7个图形需要用多少根小棒?
(3)摆第n个图形需要用多少根小棒?
假设第一个三角形的第一根小棒不动,每增加一个三角形,就增加两根小棒。
1+2×7=15(根)
答:摆第7个图形需要用15根小棒。
答:摆第n个图形需要用(1+2n)根小棒。
节日期间广场上有一排彩旗,按照1面红旗、2面黄旗、3面绿旗的顺序排列。第55面彩旗是什么颜色?第100面呢?
3
6面彩旗为一组,计算55里面有多少组这样的彩旗,看余数情况。
55÷6=9······1
100÷6=16······4
答:第55面彩旗是红色,第100面彩旗是绿色。
(1)多边形的内角和与边数有什么关系?
4
多边形
边 数
3
4
5
6
内角和
180°
360°
540°
720°
多边形里分成的三角形个数,正好是这个多边形的边数-2。
多边形内角和=(边数-2)×180°
(3)一个n边形的内角和是多少度?
(2)一个九边形的内角和是多少度?
4
多边形
边 数
3
4
5
6
内角和
180°
360°
540°
720°
(9-2)×180°=1260°
(n-2)×180°
小芳、小莉两名女生和小勇、小强两名男生站成一排拍毕业纪念照,如果男女间隔排列,一共有多少种站法?
5
(5)小莉 小勇 小芳 小强
(6)小莉 小强 小芳 小勇
(7)小芳 小勇 小莉 小强
(8)小芳 小强 小莉 小勇
方法一:用列举法
(1)小勇 小莉 小强 小芳
(2)小勇 小芳 小强 小莉
(3)小强 小莉 小勇 小芳
(4)小强 小芳 小勇 小莉
答:共有8种不同的站法。
小勇
小莉
小强
小芳
怎样才能找出所有的排列方法呢?
小芳、小莉两名女生和小勇、小强两名男生站成一排拍毕业纪念照,如果男女间隔排列,一共有多少种站法?
5
小勇
小莉
小强
小芳
怎样才能找出所有的排列方法呢?
方法二:用字母表示法
B1 B2
小勇 小强 小莉 小芳
A1 A2 B1 B2
第一位 第二位 第三位 第四位
A1 A2
答:共有8种不同的站法。
2×4=8
互换
互换
在学校运动会上,1号、2号、3号、4号运动员取得了800 m赛跑的前4名。小记者来采访他们各自的名次。1号说:“3号第一个冲过终点。”另一名运动员说:“2号不是第4名。”小裁判说:“他们的号码与他们的名次都不相同。”他们的名次各是多少?
6
第1名 第2名 第3名 第4名
1号
2号
3号
4号
√
√
×
×
√
√
答:3号第1名,4号第2名,
2号第3名,1号第4名。
警察抓住了4个犯罪嫌疑人,其中的一个人是主谋。甲说:“我不是主谋。”乙说:“丁是主谋。”丙说:“我不是主谋。”丁说:“甲是主谋。”已知他们4个人中只有1个人说了真话。主谋是
谁?
7
需要通过找出题中互相矛盾的条件关系
“甲说自己不是主谋,丙也说自己不是主谋”,从而推知其中两人的话必有真假。
假设甲说的是真话,则说明丙是主谋。
另两个人说的也是假话,与题目都相符。
答:主谋是丙。
○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
8
(1)○+□=91
△+□=63
△+○=46
(2)□-○=8
□+○=12
△=□+□+○
第一个式子减第二个式子得到
○-△=91-63=28
用这个式子加第三个式子得到
○+○=28+46
○=37
第一个式子加第二个式子得到
□+□=8+12=20
○=12-10=2
△=10+10+2=22
□=10
□=91-37=54
△= 46-37=9
如图,把三角形ABC的边BC延长到点D。
(1)∠3和∠4拼成的是什么角?
(2)你能说明∠1+∠2=∠4吗?
9
答:(1)∠3和∠4拼成的是平角。
(2)∠1+∠2+∠3=180°
∠3+∠4=180°
∠1+∠2=∠4
七桥问题
一个城市中有一条河穿过,河中有两个小岛,有七座桥连接其中。有人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥?这就是著名的七桥问题。数学家通过把七桥问题转化成一个几何问题——一笔画问题(如图),发现按上述要求一次走完七座桥的走法是不存在的。
选自教材103页练习二十二“你知道吗?”
选自教材103页练习二十二“你知道吗?”
一笔画问题
通过点的线条数目是双数,称为偶点;通过点的线条数目是单数,称为奇点。
1.图形里如果没有奇点,都可以一笔成的。
2.图形里如果只有一对奇点,那么也可以一笔画画成。
3.图形里的奇点如果是多于一对,就无法一笔画完成。
(奇点的个数为0或2的图形可以一笔画)
1.张老师有50分和80分的邮票各两枚。他用这些邮票能付多少种邮资?
1枚:50分、80分。有2种
2枚:100分、130分、160分。 有3种
3枚:180分、210分。有2种
4枚:260分。有1种
答:他用这些邮票能付8种邮资。
2.学校为艺术节选送节目,从3个合唱节目中选出2个,2个舞蹈节目中选出1个,一共有几种选送方案?
第三步:把两次选法进行搭配,共有6种选法。
第一步:从3个合唱节目中选出2个,有3种选法。
第二步:从2个舞蹈节目中选出1个,有2种选法。
方法一:
答:一共有6种选送方案。
2.学校为艺术节选送节目,从3个合唱节目中选出2个,2个舞蹈节目中选出1个,一共有几种选送方案?
如果用A、B、C表示3个合唱节目,用a、b表示2个舞蹈节目。
a
b
A
B
C
方法二:
答:一共有6种选送方案。
2.学校为艺术节选送节目,从3个合唱节目中选出2个,2个舞蹈节目中选出1个,一共有几种选送方案?
如果用A、B、C表示3个合唱节目,用a、b表示2个舞蹈节目。
方法三:
AB
BC
AC
a
b
答:一共有6种选送方案。
这节课有什么收获呢?
1.会归纳、类比、推理的思想方法,
培养数学的逻辑思维。
2.有序思考解决生活中实际问题。
1.从教材练习二十二中选取;
2.从课时练中选取。
数学思想和方法
对应思想方法
类比思想方法
假设思想方法
比较思想方法
数形结合思想方法
转化思想方法
分类思想方法
