第八章立体几何初步 综合复习训练(含解析)
文档属性
| 名称 | 第八章立体几何初步 综合复习训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 23:20:41 | ||
图片预览


文档简介
第八章立体几何初步综合复习训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
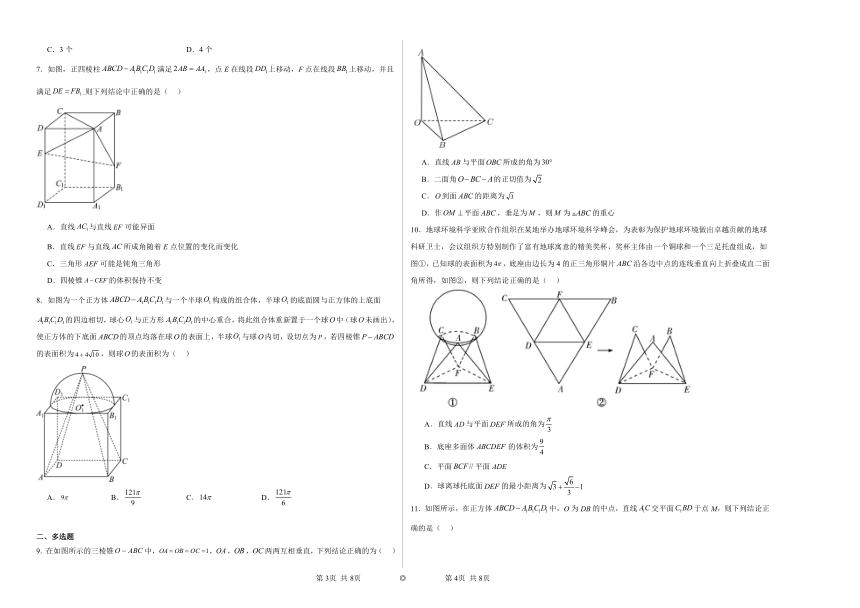
1.锐角中,角、、所对的边分别为、、,若、,,,且,则的面积为( )
A. B. C. D.
2.如图,在单位正方体中,点P是线段上的动点,给出以下四个命题:
①异面直线与直线所成角的大小为定值;
②二面角的大小为定值;
③若Q是对角线上一点,则长度的最小值为;
④若R是线段上一动点,则直线与直线不可能平行.
其中真命题有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在梯形中,且,点为线段的靠近点的一个四等分点,点为线段的中点,与交于点,且,则的值为( )
A.1 B. C. D.
4.如图,在多面体中,已知是边长为1的正方形,且均为正三角形,,则该多面体的表面积为( )
A. B. C. D.
5.如图,在棱长为a的正方体中,P在线段上,且,M为线段上的动点,则三棱锥的体积为( )
A. B. C. D.与点M的位置有关
6.如图,四棱锥的底面为矩形,底面,,,点是的中点,过,,三点的平面与平面的交线为,则下列结论中正确的有( )
(1)平面;
(2)平面;
(3)直线与所成角的余弦值为;
(4)平面截四棱锥所得的上、下两部分几何体的体积之比为.
A.1个 B.2个
C.3个 D.4个
7.如图,正四棱柱满足,点E在线段上移动,F点在线段上移动,并且满足.则下列结论中正确的是( )
A.直线与直线可能异面
B.直线与直线所成角随着E点位置的变化而变化
C.三角形可能是钝角三角形
D.四棱锥的体积保持不变
8.如图为一个正方体与一个半球构成的组合体,半球的底面圆与正方体的上底面的四边相切,球心与正方形的中心重合,将此组合体重新置于一个球中(球未画出),使正方体的下底面的顶点均落在球的表面上,半球与球内切,设切点为,若四棱锥的表面积为,则球的表面积为( )
A. B. C. D.
二、多选题
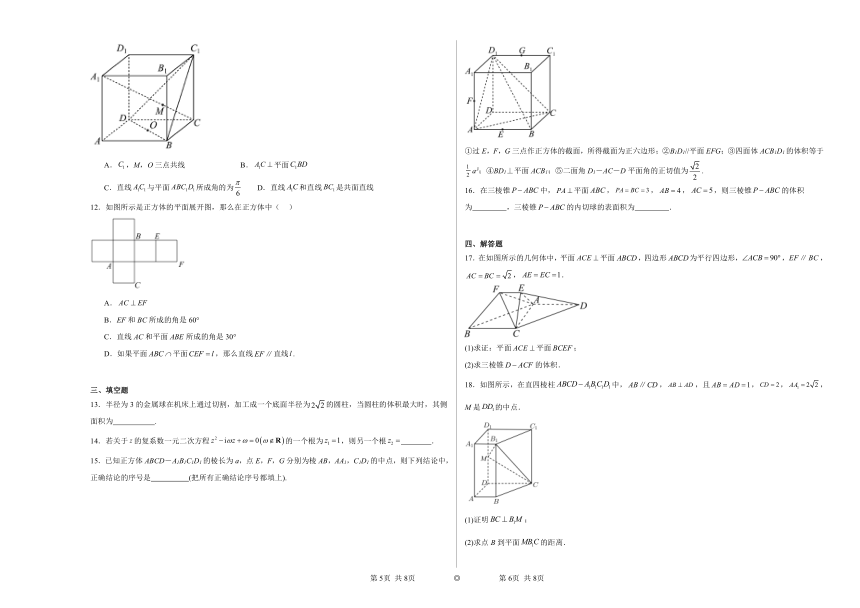
9.在如图所示的三棱锥中,,,,两两互相垂直,下列结论正确的为( )
A.直线与平面所成的角为
B.二面角的正切值为
C.到面的距离为
D.作平面,垂足为,则为的重心
10.地球环境科学亚欧合作组织在某地举办地球环境科学峰会,为表彰为保护地球环境做出卓越贡献的地球科研卫士,会议组织方特别制作了富有地球寓意的精美奖杯,奖杯主体由一个铜球和一个三足托盘组成,如图①,已知球的表面积为,底座由边长为4的正三角形铜片沿各边中点的连线垂直向上折叠成直二面角所得,如图②,则下列结论正确的是( )
A.直线与平面所成的角为
B.底座多面体的体积为
C.平面平面
D.球离球托底面的最小距离为
11.如图所示,在正方体中,O为DB的中点,直线交平面于点M,则下列结论正确的是( )
A.,M,O三点共线 B.平面
C.直线与平面所成角的为 D.直线和直线是共面直线
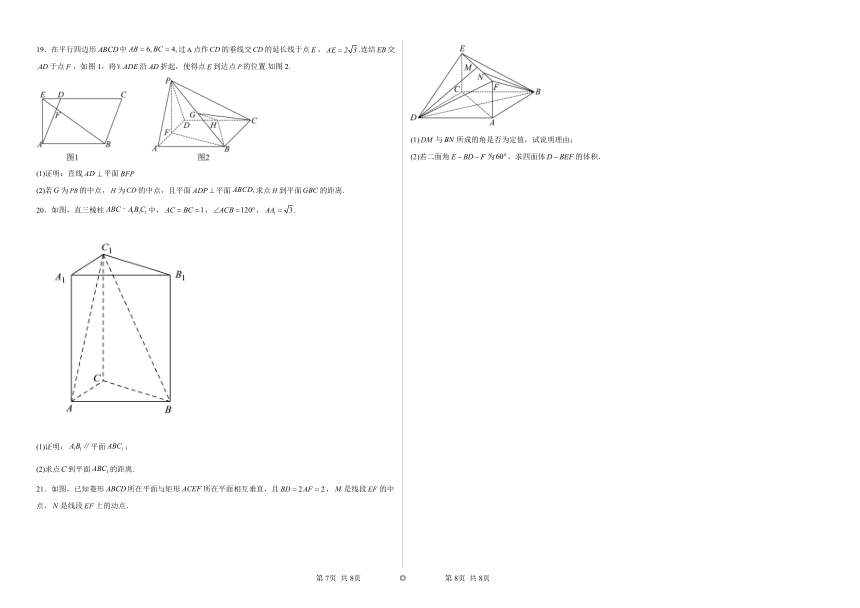
12.如图所示是正方体的平面展开图,那么在正方体中( )
A.
B.EF和BC所成的角是60°
C.直线AC和平面ABE所成的角是30°
D.如果平面平面,那么直线直线.
三、填空题
13.半径为3的金属球在机床上通过切割,加工成一个底面半径为的圆柱,当圆柱的体积最大时,其侧面积为 .
14.若关于的复系数一元二次方程的一个根为,则另一个根 .
15.已知正方体ABCD-A1B1C1D1的棱长为a,点E,F,G分别为棱AB,AA1,C1D1的中点,则下列结论中,正确结论的序号是 (把所有正确结论序号都填上).
①过E,F,G三点作正方体的截面,所得截面为正六边形;②B1D1//平面EFG;③四面体ACB1D1的体积等于a3;④BD1⊥平面ACB1;⑤二面角D1-AC-D平面角的正切值为.
16.在三棱锥中,平面,,,,则三棱锥的体积为 ,三棱锥的内切球的表面积为 .
四、解答题
17.在如图所示的几何体中,平面平面,四边形为平行四边形,,,,.
(1)求证:平面平面;
(2)求三棱锥的体积.
18.如图所示,在直四棱柱中,,,且,,,M是的中点.
(1)证明;
(2)求点B到平面的距离.
19.在平行四边形中过点作的垂线交的延长线于点,.连结交于点,如图1,将沿折起,使得点到达点的位置.如图2.
(1)证明:直线平面
(2)若为的中点,为的中点,且平面平面求点到平面的距离.
20.如图,直三棱柱中,,,.
(1)证明:平面;
(2)求点到平面的距离.
21.如图,已知菱形所在平面与矩形所在平面相互垂直,且,是线段的中点,是线段上的动点.
(1)与所成的角是否为定值,试说明理由;
(2)若二面角为,求四面体的体积.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
【分析】先由向量垂直得到,利用余弦定理求出或,利用锐角三角形排除,从而,利用面积公式求出答案.
【详解】由题意得:,故,
因为,
所以,
由余弦定理得:,
解得:或,
当时,最大值为B,其中,故为钝角,不合题意,舍去;
当时,最大值为B,其中,故B为锐角,符合题意,
此时.
故选:D
2.C
【分析】利用正方体的性质,结合空间直线与直线,直线与平面,平面与平面的位置关系,逐项判断正误.
【详解】解:对于①,由正方体的性质可知,平面,又平面,
故,异面直线与直线的所成的角为定值,①正确;
对于②,平面即为平面,平面与平面所成的二面角为定值,故二面角为定值,②正确;
对于③,将平面沿直线翻折到平面内,平面图如下,过点做,,,此时,的值最小.
由题可知,,,
,
则,,
故,又,
故的最小值为,故③正确.
对于④,在正方体中易证平面,设,则即为二面角的平面角,又正方体边长为1,故,则,由余弦定理得,故,同理,
故在上必然存在一点,使得二面角为,即平面平面,平面与平面的交线为,
则,过点作的垂线.此时平面,又平面,故.故④错误.
故选:C.
3.C
【分析】由向量的线性运算法则化简得到和,结合三点共线和三点共线,得出和,联立方程组,即可求解.
【详解】根据向量的线性运算法则,可得
,
因为三点共线,可得,即;
又由,
因为三点共线,可得,即,
联立方程组,解得,所以.
故选:C.
4.A
【分析】先证明,结合梯形面积公式求得正确答案.
【详解】由于,所以.
依题意,均为正三角形,
所以四边形和四边形是等腰梯形,
两个等腰梯形的高为.
所以多面体的表面积为:.
故选:A
5.A
【分析】根据题意可得点到平面MBC的距离为,,利用等体积法和三棱锥的体积公式即可求出.
【详解】由题意知,点到平面MBC的距离为a,又,
所以点到平面MBC的距离为,
又点M在上运动,所以,
所以,
故选:A.
6.C
【分析】对A,取的中点,连接,证明平面,即平面,可判断A;对B,若平面,则,结合,可判断B;对C, 根据,故判断C;对D,连接,分别求出两部分的体积即可判断D.
【详解】
对A,取的中点,连接,则,即,,,四点共面,即为,
因为,平面,平面,所以平面,即平面,故A正确;
对B:由,若平面.则必有,即四边形为平行四边形,则,因为,,所以矛盾,故B错误;
对C:与所成角,即与所成角,即与所成角,由底面得.则,故C正确;
对D:连接,由A知截面就是平面,下半部分分为四棱锥和三棱锥.
,,
由底面得,又,,平面,所以平面,即平面.
所以,即下半部分体积为.
所以上半部分体积与下半部分体积之比为,故D正确.
因此正确的结论有3个.
故选:C.
7.D
【分析】如图所示,连接有关线段.设M,N为AC,A1C1的中点,MN的中点为O,可得AC1与EF都是以O为中点,由此可判定A错误;利用线面垂直可以得到,从而否定B;利用勾股定理和三角形锐角钝角的判定条件计算可以判定△AEF为锐角三角形,从而否定;利用体积转化,分解方法,结合线面平行的性质可以判定.
【详解】如图所示,连接有关线段.
设M,N为AC,A1C1的中点,即为上下底面的中心,
MN的中点为O,则AC1的中点也是O,
又∵DE=B1F,由对称性可得O也是EF的中点,
所以AC1与EF交于点O,故不是异面直线,故A错误;
由正四棱柱的性质结合线面垂直的判定定理易得平面,
因为平面,∴故B错误;
设,则,设,
易得
因为
为锐角;
因为
为锐角,
因为
当时取得最小值为
为锐角,故△AEF为锐角三角形,故C错误;
三棱锥A-EFC也可以看做F-AOC和E-AOC的组合体,
由于△AOB是固定的,E,F到平面AOC的距离是不变的
(∵易知BB1,DD1平行与平面ACC1A1),故体积不变,
故D正确.
故选:D.
【点睛】本题综合考查空间的线线角,几何体体积问题,涉及利用勾股定理判定三角形内角是锐角问题(在△中,,当固定变短时,满足可得到为锐角).关键是利用计算证明时要仔细计算,严格论证,解决体积问题时,要灵活地进行体积转化与分割.
8.B
【分析】设球、半球的半径分别为、,设正方体的下底面的中心为,连接,根据已知条件求出的值,根据几何体的对称性知球的球心在线段上,进而可得出关于的方程,求出的值,利用球体的表面积公式可求得球的表面积.
【详解】设球、半球的半径分别为、,
则由正方体与半球的位置关系易知正方体的棱长为,
设正方体的下底面的中心为,连接,则四棱锥的高,
易知四棱锥为正四棱锥,则其斜高为,
由题意得,得,
根据几何体的对称性知球的球心在线段上,连接、,
在中,,,,
由勾股定理得,则,解得,
因此,球的表面积,
故选:B.
【点睛】方法点睛:解决与球相关的切、接问题,其通法是作出截面,将空间几何问题转化为平面几何问题求解,其解题思维流程如下:
(1)定球心:如果是内切球,球心到切点的距离相等且为球的半径;如果是外接球,球心到接点的距离相等且为半径;
(2)作截面:选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素的关系),达到空间问题平面化的目的;
(3)求半径下结论:根据作出截面中的几何元素,建立关于球的半径的方程,并求解.
9.BD
【分析】利用线面垂直的判定定理可得平面,可得为直线与平面所成的角,即可判断A项;利用线面垂直的判定定理可得平面,即得为二面角的平面角,即可判断B项;利用等体积法求点面距离即可判断C项;利用线面垂直得判定定理结合等边三角形的性质即可判断D项.
【详解】解:因为,,两两互相垂直,,平面,
故为直线与平面所成的角,又,所以,
故直线与平面所成的角为,故A错误;
取中点为,连接,
因为,,,两两互相垂直,所以,
因为,所以平面,故为二面角的平面角,
则,故二面角的正切值为,故B项正确;
因为,所以,设到面的距离为,
则,解得,故C项错误;
因为,故为等边三角形,
因为平面,则点为点在平面上的投影,又,
即点到顶点的距离相等,即点到顶点的距离相等,
故为的重心,故D项正确.
故选:BD.
10.ABD
【分析】根据图形的形成可知,三点在底面上的投影分别是三边中点,,,由平面可得就是直线与平面所成的角,即可判断A项;多面体的体积为直三棱柱体积减去三个相同的三棱锥,利用几何体的体积公式计算,可判断B项;利用面面平行的判定定理证明平面平面,可判断C项;由已知可得球的半径,计算球心到平面的距离,即可判断D项.
【详解】解:根据图形的形成可知,三点在底面上的投影分别是三边中点,,,如图所示,
对于A,平面,∴就是直线与平面所成的角,∵是等边三角形,∴,A正确;
对于B,将几何体补全为直三棱柱,如下图示,∴多面体的体积为直三棱柱体积减去三个相同的三棱锥,∴由下图知:,故B正确;
对于C,因为且,故四边形为平行四边形,故,
因为、分别为、的中点,则,故,
∵平面,平面,∴平面,
∵,平面,平面,∴平面,
∵,所以,平面平面,
因为过直线有且只有一个平面与平面平行,显然平面与平面不重合,
故平面与平面不平行,故C错误;
对于D,由上面讨论知,设是球心,球半径为,由得,则是正四面体,棱长为1,设是的中心,则平面,又平面,所以,,则,又.所以球离球托底面的最小距离为,D正确.
故选:ABD.
11.ABC
【分析】根据正方体的特性,依次分析各项正误.
【详解】由正方体的特性可知,为正方体的体对角线,平面,平面平面于,又交平面于点,故点在上,故A项正确;
由正方体的特性可知,平面,平面,故,同理,,于点,故平面,故B项正确;
设正方体的边长为1,直线与平面的夹角为,则,点到平面的距离为,故,,C项正确;
直线与直线为异面直线,故D项错误.
故选:ABC.
12.BCD
【分析】根据正方体的平面展开图还原正方体,利用正方体的性质,结合异面直线的位置关系,线面位置关系及面面平行的性质依次判断各项正误.
【详解】
如图,把正方体的平面展开图还原成正方体.
在正方体中,可知,
故异面直线与所成的角即为与所成的角为,故A项错误;
同理,与所成的角即为与所成的角为,故B项正确;
在正方体中,,,,,故平面,则点到平面的距离为,
设直线与平面所成的角为,则,故,故C项正确;
在正方体中,,
则平面平面,平面平面于直线,平面平面,故直线直线,故D项正确.
故选:BCD.
13.
【分析】根据题设可知圆柱体的上下底面是金属球的两个截面,求出圆柱的高,再求其侧面积.
【详解】要使圆柱的体积最大,即圆柱的高最大,
所以仅当圆柱上下底面是金属球的截面时高最大,为,
所以侧面积为.
故答案为:.
14.
【分析】代入,求解可得,结合韦达定理即得解
【详解】由题意,
故
即
故复系数一元二次方程
由韦达定理可知:
故
故答案为:
15.①④
【分析】根据平面的基本性质,可判定①正确;根据线面位置关系,可判定②不正确;根据正方体的体积减去四个三棱锥的体积,可判定③不正确;根据线面垂直的判定定理,可判定④正确;根据二面角的平面角的求法,可判定⑤不正确.
【详解】如图所示,延长分别与的延长线交于点,连接交于,
设与的延长线交于点,连接交于,交于,
连接,则截面六边形为正六边形,故①正确;
由与相交,所以和平面相交,所以②不正确;
四面体的体积等于正方体的体积减去四个三棱锥的体积,
即,所以③不正确;
因为,且与相交,所以平面,故④正确;
又由平面,所以二面角的平面角为,
所以,所以⑤不正确.
故选:①④.
【点睛】解答此类问题常见的误区:
1、对空间平行关系的转化条件理解不透导致错误;
2、对面面平行判定定理的条件“面内两相交直线”认识不清导致错解;
3、对面面平行性质定理理解不深导致错解.
16. 6 /
【分析】根据已知条件可得,利用三棱锥的体积公式结算即可;利用线面垂直的判定定理可证明平面,设内切球半径为,利用等体积法求解内切球的半径,利用球的表面积公式结算即可.
【详解】解:因为,,,在中,,
所以,又平面,所以,
因为平面,平面,所以,,,故
又,,所以平面,
又平面,所以,
所以均为直角三角形,
设三棱锥的内切球的球心为,半径为,
则,
即,
解得,故三棱锥的内切球的表面积.
故答案为:6;.
17.(1)证明见解析
(2)
【分析】(1)由已知可得,结合面面垂直可得平面,利用面面垂直的判定定理即可证明;
(2)先求解点到平面的距离,再求解的面积,利用锥体的体积公式即可求解.
【详解】(1)解:∵,∴,
∵平面平面,且平面平面,
平面,∴平面,
∵平面,∴平面平面.
(2)取的中点,连接,∵,∴,
∵平面平面,∴平面,
∵,平面,平面,
∴平面,所以点到平面的距离等于点到平面的距离,
即点到平面的距离为的长.
∵,,∴,
∴,从而,
∵四边形为平行四边形,,
∴,,
∴,
∴.
18.(1)证明见解析
(2)
【分析】(1)根据线面垂直的判定定理证明平面,利用线面垂直证明线线垂直即可;
(2)利用等体积法求解店面距离即可.
【详解】(1)如图、连接BD,
∵,,∴,
∴,∴.
∵平面ABCD,∴,
又,∴平面,
∵平面,∴.
(2)解:连接BM,.
由已知可得,,,
∴,∴.
设点B到平面的距离为h,
由(1)知BC⊥平面,
∴三棱锥的体积,
即,
解得,即点B到平面的距离为.
19.(1)证明见解析
(2)
【分析】(1)在平面图中证明,在立体图中利用线面垂直的判定定理即可求解.
(2)利用线面垂直的判定定理证明平面,可得为三棱锥的高,计算的值,进而计算三棱锥的体积,然后计算的面积,利用等体积法求解点到平面的距离即可.
【详解】(1)证明:图1中,在中,所以.所以
也是直角三角形,
,
在图2中,所以平面.
(2)解:∵平面平面,且平面平面,
平面,平面.
取的中点为,连结则
平面,即为三棱锥的高.
.
,
又,,又,
平面,,
设点到平面的距离为,则由,
得,解得.
点到平面的距离为.
20.(1)证明见解析
(2)
【分析】(1)利用线面平行的判定定理即可求解;
(2)利用等体积法求解点到平面的距离即可.
【详解】(1)证明:∵为直三棱柱,∴
又平面,平面,
∴平面
(2)解:在中,,,
则,的面积为
∵为直三棱柱,∴平面,
∴,从而
取的中点,连接,则,
∴的面积为,
设点到平面的距离为,
由于
∴,解得
故点到平面的距离为.
21.(1)与所成角为定值,理由见解析
(2)
【分析】(1)利用线面垂直的判定定理可证明平面,由线面垂直证明线线垂直,即可确定与所成角为定值;
(2)根据题意可得为二面角的平面角,即可求解各边长度,利用棱锥的体积公式即可求解.
【详解】(1)解:(1)因为平面平面,,
所以平面,
∵平面,所以,同理可证.
又为菱形,,
所以≌,.
又为的中点,所以.
设,连接,,所以.
又,所以平面.
又平面,所以,
故与所成角为定值.
(2)解:∵,为中点,
∴,为二面角的平面角,所以,
由题意知,解得,
又,可得,
由(1)得平面,
所以四面体的体积为:
.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.锐角中,角、、所对的边分别为、、,若、,,,且,则的面积为( )
A. B. C. D.
2.如图,在单位正方体中,点P是线段上的动点,给出以下四个命题:
①异面直线与直线所成角的大小为定值;
②二面角的大小为定值;
③若Q是对角线上一点,则长度的最小值为;
④若R是线段上一动点,则直线与直线不可能平行.
其中真命题有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在梯形中,且,点为线段的靠近点的一个四等分点,点为线段的中点,与交于点,且,则的值为( )
A.1 B. C. D.
4.如图,在多面体中,已知是边长为1的正方形,且均为正三角形,,则该多面体的表面积为( )
A. B. C. D.
5.如图,在棱长为a的正方体中,P在线段上,且,M为线段上的动点,则三棱锥的体积为( )
A. B. C. D.与点M的位置有关
6.如图,四棱锥的底面为矩形,底面,,,点是的中点,过,,三点的平面与平面的交线为,则下列结论中正确的有( )
(1)平面;
(2)平面;
(3)直线与所成角的余弦值为;
(4)平面截四棱锥所得的上、下两部分几何体的体积之比为.
A.1个 B.2个
C.3个 D.4个
7.如图,正四棱柱满足,点E在线段上移动,F点在线段上移动,并且满足.则下列结论中正确的是( )
A.直线与直线可能异面
B.直线与直线所成角随着E点位置的变化而变化
C.三角形可能是钝角三角形
D.四棱锥的体积保持不变
8.如图为一个正方体与一个半球构成的组合体,半球的底面圆与正方体的上底面的四边相切,球心与正方形的中心重合,将此组合体重新置于一个球中(球未画出),使正方体的下底面的顶点均落在球的表面上,半球与球内切,设切点为,若四棱锥的表面积为,则球的表面积为( )
A. B. C. D.
二、多选题
9.在如图所示的三棱锥中,,,,两两互相垂直,下列结论正确的为( )
A.直线与平面所成的角为
B.二面角的正切值为
C.到面的距离为
D.作平面,垂足为,则为的重心
10.地球环境科学亚欧合作组织在某地举办地球环境科学峰会,为表彰为保护地球环境做出卓越贡献的地球科研卫士,会议组织方特别制作了富有地球寓意的精美奖杯,奖杯主体由一个铜球和一个三足托盘组成,如图①,已知球的表面积为,底座由边长为4的正三角形铜片沿各边中点的连线垂直向上折叠成直二面角所得,如图②,则下列结论正确的是( )
A.直线与平面所成的角为
B.底座多面体的体积为
C.平面平面
D.球离球托底面的最小距离为
11.如图所示,在正方体中,O为DB的中点,直线交平面于点M,则下列结论正确的是( )
A.,M,O三点共线 B.平面
C.直线与平面所成角的为 D.直线和直线是共面直线
12.如图所示是正方体的平面展开图,那么在正方体中( )
A.
B.EF和BC所成的角是60°
C.直线AC和平面ABE所成的角是30°
D.如果平面平面,那么直线直线.
三、填空题
13.半径为3的金属球在机床上通过切割,加工成一个底面半径为的圆柱,当圆柱的体积最大时,其侧面积为 .
14.若关于的复系数一元二次方程的一个根为,则另一个根 .
15.已知正方体ABCD-A1B1C1D1的棱长为a,点E,F,G分别为棱AB,AA1,C1D1的中点,则下列结论中,正确结论的序号是 (把所有正确结论序号都填上).
①过E,F,G三点作正方体的截面,所得截面为正六边形;②B1D1//平面EFG;③四面体ACB1D1的体积等于a3;④BD1⊥平面ACB1;⑤二面角D1-AC-D平面角的正切值为.
16.在三棱锥中,平面,,,,则三棱锥的体积为 ,三棱锥的内切球的表面积为 .
四、解答题
17.在如图所示的几何体中,平面平面,四边形为平行四边形,,,,.
(1)求证:平面平面;
(2)求三棱锥的体积.
18.如图所示,在直四棱柱中,,,且,,,M是的中点.
(1)证明;
(2)求点B到平面的距离.
19.在平行四边形中过点作的垂线交的延长线于点,.连结交于点,如图1,将沿折起,使得点到达点的位置.如图2.
(1)证明:直线平面
(2)若为的中点,为的中点,且平面平面求点到平面的距离.
20.如图,直三棱柱中,,,.
(1)证明:平面;
(2)求点到平面的距离.
21.如图,已知菱形所在平面与矩形所在平面相互垂直,且,是线段的中点,是线段上的动点.
(1)与所成的角是否为定值,试说明理由;
(2)若二面角为,求四面体的体积.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
【分析】先由向量垂直得到,利用余弦定理求出或,利用锐角三角形排除,从而,利用面积公式求出答案.
【详解】由题意得:,故,
因为,
所以,
由余弦定理得:,
解得:或,
当时,最大值为B,其中,故为钝角,不合题意,舍去;
当时,最大值为B,其中,故B为锐角,符合题意,
此时.
故选:D
2.C
【分析】利用正方体的性质,结合空间直线与直线,直线与平面,平面与平面的位置关系,逐项判断正误.
【详解】解:对于①,由正方体的性质可知,平面,又平面,
故,异面直线与直线的所成的角为定值,①正确;
对于②,平面即为平面,平面与平面所成的二面角为定值,故二面角为定值,②正确;
对于③,将平面沿直线翻折到平面内,平面图如下,过点做,,,此时,的值最小.
由题可知,,,
,
则,,
故,又,
故的最小值为,故③正确.
对于④,在正方体中易证平面,设,则即为二面角的平面角,又正方体边长为1,故,则,由余弦定理得,故,同理,
故在上必然存在一点,使得二面角为,即平面平面,平面与平面的交线为,
则,过点作的垂线.此时平面,又平面,故.故④错误.
故选:C.
3.C
【分析】由向量的线性运算法则化简得到和,结合三点共线和三点共线,得出和,联立方程组,即可求解.
【详解】根据向量的线性运算法则,可得
,
因为三点共线,可得,即;
又由,
因为三点共线,可得,即,
联立方程组,解得,所以.
故选:C.
4.A
【分析】先证明,结合梯形面积公式求得正确答案.
【详解】由于,所以.
依题意,均为正三角形,
所以四边形和四边形是等腰梯形,
两个等腰梯形的高为.
所以多面体的表面积为:.
故选:A
5.A
【分析】根据题意可得点到平面MBC的距离为,,利用等体积法和三棱锥的体积公式即可求出.
【详解】由题意知,点到平面MBC的距离为a,又,
所以点到平面MBC的距离为,
又点M在上运动,所以,
所以,
故选:A.
6.C
【分析】对A,取的中点,连接,证明平面,即平面,可判断A;对B,若平面,则,结合,可判断B;对C, 根据,故判断C;对D,连接,分别求出两部分的体积即可判断D.
【详解】
对A,取的中点,连接,则,即,,,四点共面,即为,
因为,平面,平面,所以平面,即平面,故A正确;
对B:由,若平面.则必有,即四边形为平行四边形,则,因为,,所以矛盾,故B错误;
对C:与所成角,即与所成角,即与所成角,由底面得.则,故C正确;
对D:连接,由A知截面就是平面,下半部分分为四棱锥和三棱锥.
,,
由底面得,又,,平面,所以平面,即平面.
所以,即下半部分体积为.
所以上半部分体积与下半部分体积之比为,故D正确.
因此正确的结论有3个.
故选:C.
7.D
【分析】如图所示,连接有关线段.设M,N为AC,A1C1的中点,MN的中点为O,可得AC1与EF都是以O为中点,由此可判定A错误;利用线面垂直可以得到,从而否定B;利用勾股定理和三角形锐角钝角的判定条件计算可以判定△AEF为锐角三角形,从而否定;利用体积转化,分解方法,结合线面平行的性质可以判定.
【详解】如图所示,连接有关线段.
设M,N为AC,A1C1的中点,即为上下底面的中心,
MN的中点为O,则AC1的中点也是O,
又∵DE=B1F,由对称性可得O也是EF的中点,
所以AC1与EF交于点O,故不是异面直线,故A错误;
由正四棱柱的性质结合线面垂直的判定定理易得平面,
因为平面,∴故B错误;
设,则,设,
易得
因为
为锐角;
因为
为锐角,
因为
当时取得最小值为
为锐角,故△AEF为锐角三角形,故C错误;
三棱锥A-EFC也可以看做F-AOC和E-AOC的组合体,
由于△AOB是固定的,E,F到平面AOC的距离是不变的
(∵易知BB1,DD1平行与平面ACC1A1),故体积不变,
故D正确.
故选:D.
【点睛】本题综合考查空间的线线角,几何体体积问题,涉及利用勾股定理判定三角形内角是锐角问题(在△中,,当固定变短时,满足可得到为锐角).关键是利用计算证明时要仔细计算,严格论证,解决体积问题时,要灵活地进行体积转化与分割.
8.B
【分析】设球、半球的半径分别为、,设正方体的下底面的中心为,连接,根据已知条件求出的值,根据几何体的对称性知球的球心在线段上,进而可得出关于的方程,求出的值,利用球体的表面积公式可求得球的表面积.
【详解】设球、半球的半径分别为、,
则由正方体与半球的位置关系易知正方体的棱长为,
设正方体的下底面的中心为,连接,则四棱锥的高,
易知四棱锥为正四棱锥,则其斜高为,
由题意得,得,
根据几何体的对称性知球的球心在线段上,连接、,
在中,,,,
由勾股定理得,则,解得,
因此,球的表面积,
故选:B.
【点睛】方法点睛:解决与球相关的切、接问题,其通法是作出截面,将空间几何问题转化为平面几何问题求解,其解题思维流程如下:
(1)定球心:如果是内切球,球心到切点的距离相等且为球的半径;如果是外接球,球心到接点的距离相等且为半径;
(2)作截面:选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素的关系),达到空间问题平面化的目的;
(3)求半径下结论:根据作出截面中的几何元素,建立关于球的半径的方程,并求解.
9.BD
【分析】利用线面垂直的判定定理可得平面,可得为直线与平面所成的角,即可判断A项;利用线面垂直的判定定理可得平面,即得为二面角的平面角,即可判断B项;利用等体积法求点面距离即可判断C项;利用线面垂直得判定定理结合等边三角形的性质即可判断D项.
【详解】解:因为,,两两互相垂直,,平面,
故为直线与平面所成的角,又,所以,
故直线与平面所成的角为,故A错误;
取中点为,连接,
因为,,,两两互相垂直,所以,
因为,所以平面,故为二面角的平面角,
则,故二面角的正切值为,故B项正确;
因为,所以,设到面的距离为,
则,解得,故C项错误;
因为,故为等边三角形,
因为平面,则点为点在平面上的投影,又,
即点到顶点的距离相等,即点到顶点的距离相等,
故为的重心,故D项正确.
故选:BD.
10.ABD
【分析】根据图形的形成可知,三点在底面上的投影分别是三边中点,,,由平面可得就是直线与平面所成的角,即可判断A项;多面体的体积为直三棱柱体积减去三个相同的三棱锥,利用几何体的体积公式计算,可判断B项;利用面面平行的判定定理证明平面平面,可判断C项;由已知可得球的半径,计算球心到平面的距离,即可判断D项.
【详解】解:根据图形的形成可知,三点在底面上的投影分别是三边中点,,,如图所示,
对于A,平面,∴就是直线与平面所成的角,∵是等边三角形,∴,A正确;
对于B,将几何体补全为直三棱柱,如下图示,∴多面体的体积为直三棱柱体积减去三个相同的三棱锥,∴由下图知:,故B正确;
对于C,因为且,故四边形为平行四边形,故,
因为、分别为、的中点,则,故,
∵平面,平面,∴平面,
∵,平面,平面,∴平面,
∵,所以,平面平面,
因为过直线有且只有一个平面与平面平行,显然平面与平面不重合,
故平面与平面不平行,故C错误;
对于D,由上面讨论知,设是球心,球半径为,由得,则是正四面体,棱长为1,设是的中心,则平面,又平面,所以,,则,又.所以球离球托底面的最小距离为,D正确.
故选:ABD.
11.ABC
【分析】根据正方体的特性,依次分析各项正误.
【详解】由正方体的特性可知,为正方体的体对角线,平面,平面平面于,又交平面于点,故点在上,故A项正确;
由正方体的特性可知,平面,平面,故,同理,,于点,故平面,故B项正确;
设正方体的边长为1,直线与平面的夹角为,则,点到平面的距离为,故,,C项正确;
直线与直线为异面直线,故D项错误.
故选:ABC.
12.BCD
【分析】根据正方体的平面展开图还原正方体,利用正方体的性质,结合异面直线的位置关系,线面位置关系及面面平行的性质依次判断各项正误.
【详解】
如图,把正方体的平面展开图还原成正方体.
在正方体中,可知,
故异面直线与所成的角即为与所成的角为,故A项错误;
同理,与所成的角即为与所成的角为,故B项正确;
在正方体中,,,,,故平面,则点到平面的距离为,
设直线与平面所成的角为,则,故,故C项正确;
在正方体中,,
则平面平面,平面平面于直线,平面平面,故直线直线,故D项正确.
故选:BCD.
13.
【分析】根据题设可知圆柱体的上下底面是金属球的两个截面,求出圆柱的高,再求其侧面积.
【详解】要使圆柱的体积最大,即圆柱的高最大,
所以仅当圆柱上下底面是金属球的截面时高最大,为,
所以侧面积为.
故答案为:.
14.
【分析】代入,求解可得,结合韦达定理即得解
【详解】由题意,
故
即
故复系数一元二次方程
由韦达定理可知:
故
故答案为:
15.①④
【分析】根据平面的基本性质,可判定①正确;根据线面位置关系,可判定②不正确;根据正方体的体积减去四个三棱锥的体积,可判定③不正确;根据线面垂直的判定定理,可判定④正确;根据二面角的平面角的求法,可判定⑤不正确.
【详解】如图所示,延长分别与的延长线交于点,连接交于,
设与的延长线交于点,连接交于,交于,
连接,则截面六边形为正六边形,故①正确;
由与相交,所以和平面相交,所以②不正确;
四面体的体积等于正方体的体积减去四个三棱锥的体积,
即,所以③不正确;
因为,且与相交,所以平面,故④正确;
又由平面,所以二面角的平面角为,
所以,所以⑤不正确.
故选:①④.
【点睛】解答此类问题常见的误区:
1、对空间平行关系的转化条件理解不透导致错误;
2、对面面平行判定定理的条件“面内两相交直线”认识不清导致错解;
3、对面面平行性质定理理解不深导致错解.
16. 6 /
【分析】根据已知条件可得,利用三棱锥的体积公式结算即可;利用线面垂直的判定定理可证明平面,设内切球半径为,利用等体积法求解内切球的半径,利用球的表面积公式结算即可.
【详解】解:因为,,,在中,,
所以,又平面,所以,
因为平面,平面,所以,,,故
又,,所以平面,
又平面,所以,
所以均为直角三角形,
设三棱锥的内切球的球心为,半径为,
则,
即,
解得,故三棱锥的内切球的表面积.
故答案为:6;.
17.(1)证明见解析
(2)
【分析】(1)由已知可得,结合面面垂直可得平面,利用面面垂直的判定定理即可证明;
(2)先求解点到平面的距离,再求解的面积,利用锥体的体积公式即可求解.
【详解】(1)解:∵,∴,
∵平面平面,且平面平面,
平面,∴平面,
∵平面,∴平面平面.
(2)取的中点,连接,∵,∴,
∵平面平面,∴平面,
∵,平面,平面,
∴平面,所以点到平面的距离等于点到平面的距离,
即点到平面的距离为的长.
∵,,∴,
∴,从而,
∵四边形为平行四边形,,
∴,,
∴,
∴.
18.(1)证明见解析
(2)
【分析】(1)根据线面垂直的判定定理证明平面,利用线面垂直证明线线垂直即可;
(2)利用等体积法求解店面距离即可.
【详解】(1)如图、连接BD,
∵,,∴,
∴,∴.
∵平面ABCD,∴,
又,∴平面,
∵平面,∴.
(2)解:连接BM,.
由已知可得,,,
∴,∴.
设点B到平面的距离为h,
由(1)知BC⊥平面,
∴三棱锥的体积,
即,
解得,即点B到平面的距离为.
19.(1)证明见解析
(2)
【分析】(1)在平面图中证明,在立体图中利用线面垂直的判定定理即可求解.
(2)利用线面垂直的判定定理证明平面,可得为三棱锥的高,计算的值,进而计算三棱锥的体积,然后计算的面积,利用等体积法求解点到平面的距离即可.
【详解】(1)证明:图1中,在中,所以.所以
也是直角三角形,
,
在图2中,所以平面.
(2)解:∵平面平面,且平面平面,
平面,平面.
取的中点为,连结则
平面,即为三棱锥的高.
.
,
又,,又,
平面,,
设点到平面的距离为,则由,
得,解得.
点到平面的距离为.
20.(1)证明见解析
(2)
【分析】(1)利用线面平行的判定定理即可求解;
(2)利用等体积法求解点到平面的距离即可.
【详解】(1)证明:∵为直三棱柱,∴
又平面,平面,
∴平面
(2)解:在中,,,
则,的面积为
∵为直三棱柱,∴平面,
∴,从而
取的中点,连接,则,
∴的面积为,
设点到平面的距离为,
由于
∴,解得
故点到平面的距离为.
21.(1)与所成角为定值,理由见解析
(2)
【分析】(1)利用线面垂直的判定定理可证明平面,由线面垂直证明线线垂直,即可确定与所成角为定值;
(2)根据题意可得为二面角的平面角,即可求解各边长度,利用棱锥的体积公式即可求解.
【详解】(1)解:(1)因为平面平面,,
所以平面,
∵平面,所以,同理可证.
又为菱形,,
所以≌,.
又为的中点,所以.
设,连接,,所以.
又,所以平面.
又平面,所以,
故与所成角为定值.
(2)解:∵,为中点,
∴,为二面角的平面角,所以,
由题意知,解得,
又,可得,
由(1)得平面,
所以四面体的体积为:
.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
