4.1.3 解比例 课件-人教版数学六年级下册(共20张PPT)
文档属性
| 名称 | 4.1.3 解比例 课件-人教版数学六年级下册(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 04:10:53 | ||
图片预览





文档简介
(共20张PPT)
第3课时 解比例
第四单元 比例
下面的括号里分别填几呢?
根据比例的基本性质,两个外项的积等于两个内项的积,3×6=18,18÷2=9。
( )∶3=6∶2
0.9∶3=( )∶5
9
1.5
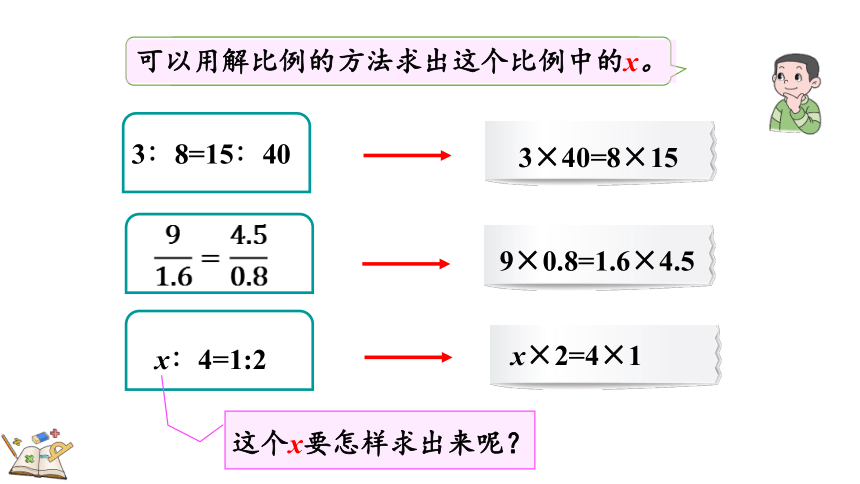
你能把下列各比改写为乘法等式吗?
9×0.8=1.6×4.5
x×2=4×1
3∶8=15∶40
x∶4=1:2
3×40=8×15
这个x要怎样求出来呢?
可以用解比例的方法求出这个比例中的x。
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的那个未知项。求比例中的未知项,叫作解比例。
你知道什么叫解比例吗?
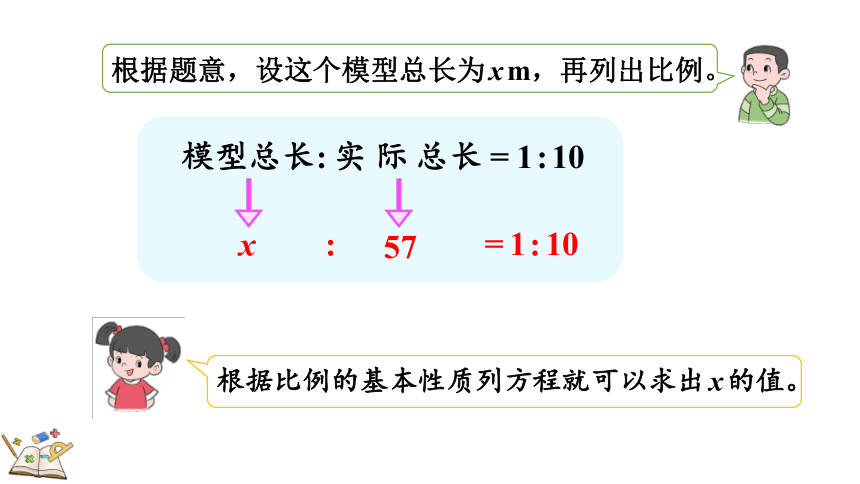
根据题意找到比例关系如下:
长征五号运载火箭总长约为57m。有一个长征五号运载火箭的模型,它的总长与火箭总长的比是1:10。这个模型总长约为多少米?
2
模型总长∶实际总长=1∶ 10
57
模型总长:实际总长=1:10
x
:
57
=
1
10
:
根据题意,设这个模型总长为xm,再列出比例。
根据比例的基本性质列方程就可以求出x的值。
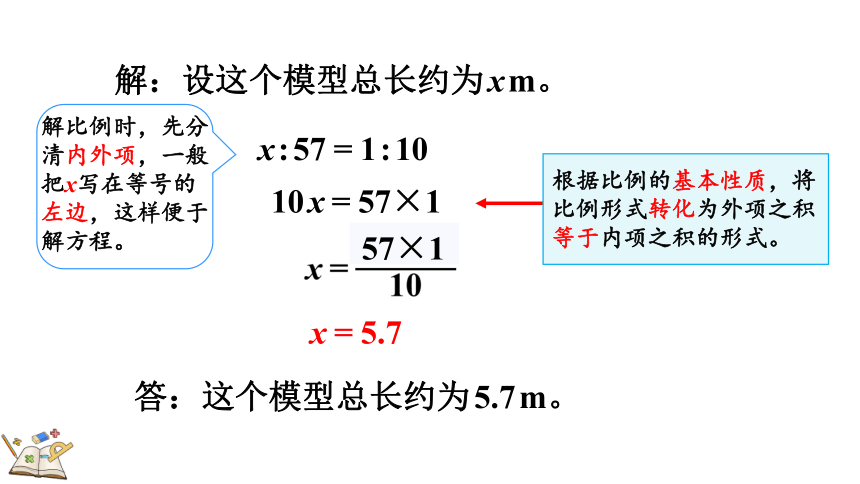
解:设这个模型总长约为xm。
x:57=1:10
10x=57×1
x=5.7
答:这个模型总长约为5.7m。
57×1
根据比例的基本性质,将比例形式转化为外项之积等于内项之积的形式。
解比例时,先分清内外项,一般把x写在等号的左边,这样便于解方程。
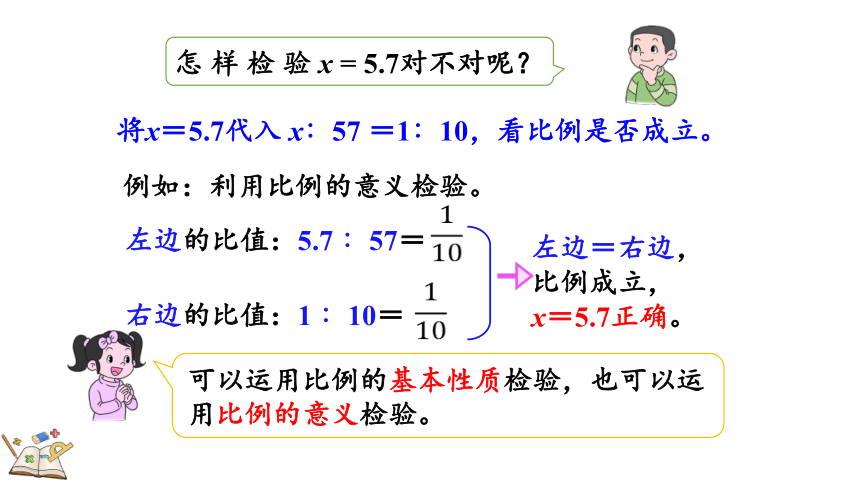
可以运用比例的基本性质检验,也可以运用比例的意义检验。
怎样检验x=5.7对不对呢?
将x=5.7代入 x∶57 =1∶10,看比例是否成立。
例如:利用比例的意义检验。
左边的比值:5.7 ∶57=
右边的比值:1 ∶10=
左边=右边,比例成立,
x=5.7正确。
①找出等量关系,根据等量关系列出比例,设x;
②根据比例的基本性质,将比相等转化为积相等;
③解方程,对所求未知数进行验证;
④写出答语。
用比例解决问题的一般步骤。
把等号两边的分子和分母交叉相乘。
3
=
解比例
解:
2.4x=1.5×6
x=( )
1.5
6
2.4
3.75
检验x的解是否正确。
将 代入比例,得到2.4∶1.5=6∶3.75 。
x=3.75
外项积:2.4× =9
3.75
内项积:1.5×6=9
外项积=内项积,x=3.75正确
选自教材第40页做一做第1题
1
(2)0.4:x=1.2:2
解比例。
x=7.5
1.2x=0.4×2
解:
解:
1
选自教材第40页做一做第1题
解比例。
12x=2.4×3
x=0.6
注意:解题时要写“解”字,等号要对齐,最后代入验证哦!
解:
2
餐馆给餐具消毒,要用100mL消毒液配成消毒水,
如果消毒液与水的比是1:150,应加入多少升水?
选自教材第40页做一做第2题
解:设应加水xmL。
100:x=1:150
x=150×100
x=15000
答:应加入15升水。
消毒液∶水 = 1∶150
15000 mL=15 L
一个秦代高级军吏俑模型的高度与实际高度的比是1∶10。模型高度是19.6 cm。这个高级军吏俑的实际高度是多少?
解:设这个高级军吏俑的实际高度是x cm。
19.6∶x=1∶10
x=196
答:这个高级军吏俑的实际高度是196 cm。
1.
超市运来橘子和苹果共152筐,橘子和苹果筐数的比是
5∶3。运来橘子和苹果各多少筐
解: 设运来橘子x筐,则运来的苹果为(152-x)筐。
x∶ (152-x) =5∶3
3x=5×(152-x)
8x=760
x=95
苹果:152-95=57(筐)
答:运来橘子95筐,苹果57筐。
2.
甲在60 m赛跑中冲过终点线时,比乙领先10 m,比丙领先20 m。如果乙和丙按各自原来的速度继续冲向终点,那么当乙到达终点时,将比丙领先几米?
解:设当乙到达终点时,丙跑了x m。
=
50 60×40
=48
6048=12(m) 答:将比丙领先12米。
这节课有什么收获呢?
解比例
列比例的关键是找到对应关系的两个比,解比例的依据是比例的基本性质。
利用比例的基本性质解比例,先把比例转化为等积式,再通过解方程求出未知项的值。
1.教材第41页练习八第3题;
2.从课时练中选取。
解比例
找比例关系,列出比例,解比例。
解比例:
比例的基本性质
第3课时 解比例
第四单元 比例
下面的括号里分别填几呢?
根据比例的基本性质,两个外项的积等于两个内项的积,3×6=18,18÷2=9。
( )∶3=6∶2
0.9∶3=( )∶5
9
1.5
你能把下列各比改写为乘法等式吗?
9×0.8=1.6×4.5
x×2=4×1
3∶8=15∶40
x∶4=1:2
3×40=8×15
这个x要怎样求出来呢?
可以用解比例的方法求出这个比例中的x。
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的那个未知项。求比例中的未知项,叫作解比例。
你知道什么叫解比例吗?
根据题意找到比例关系如下:
长征五号运载火箭总长约为57m。有一个长征五号运载火箭的模型,它的总长与火箭总长的比是1:10。这个模型总长约为多少米?
2
模型总长∶实际总长=1∶ 10
57
模型总长:实际总长=1:10
x
:
57
=
1
10
:
根据题意,设这个模型总长为xm,再列出比例。
根据比例的基本性质列方程就可以求出x的值。
解:设这个模型总长约为xm。
x:57=1:10
10x=57×1
x=5.7
答:这个模型总长约为5.7m。
57×1
根据比例的基本性质,将比例形式转化为外项之积等于内项之积的形式。
解比例时,先分清内外项,一般把x写在等号的左边,这样便于解方程。
可以运用比例的基本性质检验,也可以运用比例的意义检验。
怎样检验x=5.7对不对呢?
将x=5.7代入 x∶57 =1∶10,看比例是否成立。
例如:利用比例的意义检验。
左边的比值:5.7 ∶57=
右边的比值:1 ∶10=
左边=右边,比例成立,
x=5.7正确。
①找出等量关系,根据等量关系列出比例,设x;
②根据比例的基本性质,将比相等转化为积相等;
③解方程,对所求未知数进行验证;
④写出答语。
用比例解决问题的一般步骤。
把等号两边的分子和分母交叉相乘。
3
=
解比例
解:
2.4x=1.5×6
x=( )
1.5
6
2.4
3.75
检验x的解是否正确。
将 代入比例,得到2.4∶1.5=6∶3.75 。
x=3.75
外项积:2.4× =9
3.75
内项积:1.5×6=9
外项积=内项积,x=3.75正确
选自教材第40页做一做第1题
1
(2)0.4:x=1.2:2
解比例。
x=7.5
1.2x=0.4×2
解:
解:
1
选自教材第40页做一做第1题
解比例。
12x=2.4×3
x=0.6
注意:解题时要写“解”字,等号要对齐,最后代入验证哦!
解:
2
餐馆给餐具消毒,要用100mL消毒液配成消毒水,
如果消毒液与水的比是1:150,应加入多少升水?
选自教材第40页做一做第2题
解:设应加水xmL。
100:x=1:150
x=150×100
x=15000
答:应加入15升水。
消毒液∶水 = 1∶150
15000 mL=15 L
一个秦代高级军吏俑模型的高度与实际高度的比是1∶10。模型高度是19.6 cm。这个高级军吏俑的实际高度是多少?
解:设这个高级军吏俑的实际高度是x cm。
19.6∶x=1∶10
x=196
答:这个高级军吏俑的实际高度是196 cm。
1.
超市运来橘子和苹果共152筐,橘子和苹果筐数的比是
5∶3。运来橘子和苹果各多少筐
解: 设运来橘子x筐,则运来的苹果为(152-x)筐。
x∶ (152-x) =5∶3
3x=5×(152-x)
8x=760
x=95
苹果:152-95=57(筐)
答:运来橘子95筐,苹果57筐。
2.
甲在60 m赛跑中冲过终点线时,比乙领先10 m,比丙领先20 m。如果乙和丙按各自原来的速度继续冲向终点,那么当乙到达终点时,将比丙领先几米?
解:设当乙到达终点时,丙跑了x m。
=
50 60×40
=48
6048=12(m) 答:将比丙领先12米。
这节课有什么收获呢?
解比例
列比例的关键是找到对应关系的两个比,解比例的依据是比例的基本性质。
利用比例的基本性质解比例,先把比例转化为等积式,再通过解方程求出未知项的值。
1.教材第41页练习八第3题;
2.从课时练中选取。
解比例
找比例关系,列出比例,解比例。
解比例:
比例的基本性质
