4.1.4 练习八 课件-人教版数学六年级下册(共38张PPT)
文档属性
| 名称 | 4.1.4 练习八 课件-人教版数学六年级下册(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 00:00:00 | ||
图片预览







文档简介
(共38张PPT)
第4课时 练习八
第四单元 比例
比例的意义
2.4:1.6=60:40
像这样表示两个比相等的式子叫作比例。
用字母表示:
a∶b=c∶d(b,d≠0)
=
或
比例的各部分名称
组成比例的四个数,叫作比例的项,两端的两项叫作比例的外项,中间的两项叫作比例的内项。
2.4
1.6
60
40
=
内项
内项
外项
外项
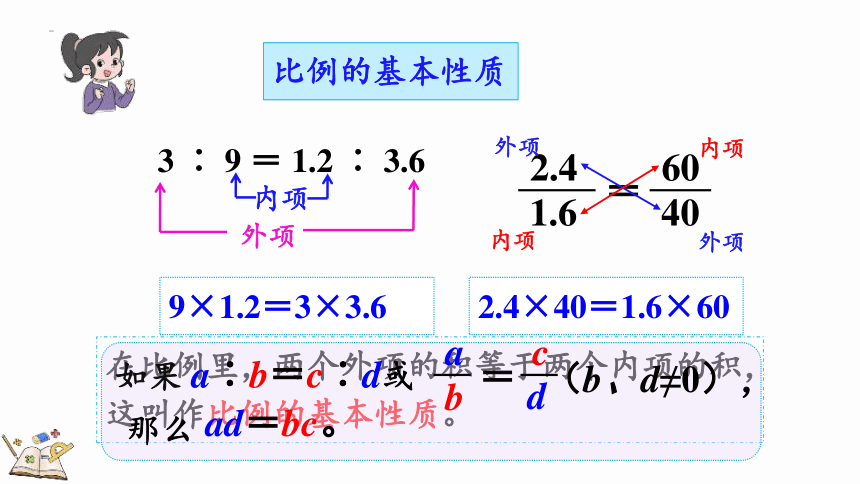
比例的基本性质
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
内项
外项
3 ∶ 9 = 1.2 ∶ 3.6
2.4×40=1.6×60
9×1.2=3×3.6
2.4
1.6
60
40
=
内项
内项
外项
外项
ad=bc。
如果 a∶b=c∶d或
a
b
c
d
=
(b、d≠0),
那么
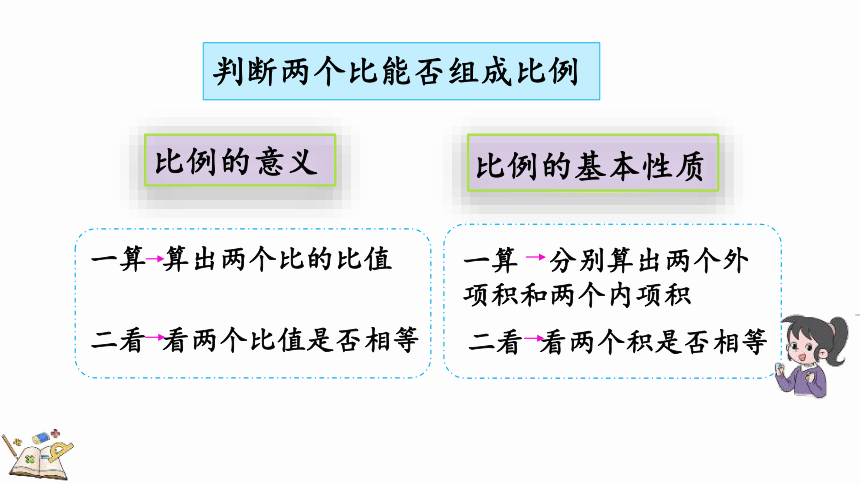
判断两个比能否组成比例
比例的意义
比例的基本性质
一算 算出两个比的比值
二看 看两个比值是否相等
一算 分别算出两个外项积和两个内项积
二看 看两个积是否相等
解比例
先把比例转化成外项乘积与内项乘积相等的形式(即方程)。
解比例的方法:根据比例的基本性质解比例。
再通过解方程求出未知项的值。
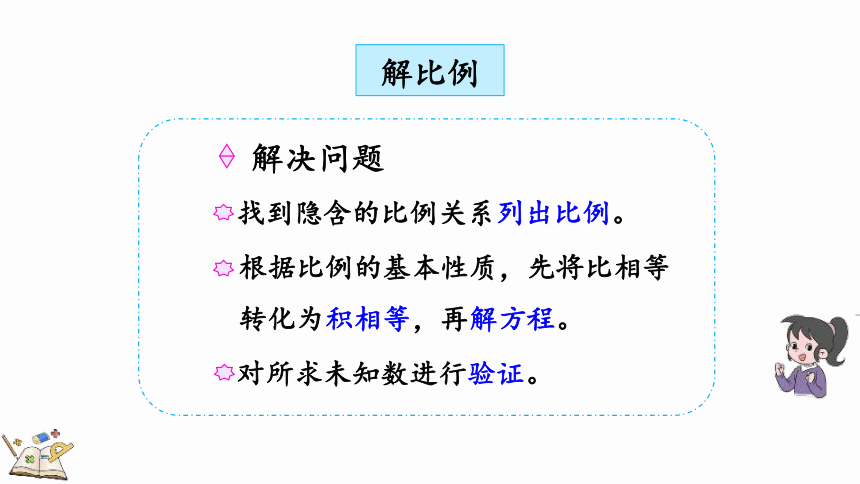
解比例
找到隐含的比例关系列出比例。
根据比例的基本性质,先将比相等转化为积相等,再解方程。
对所求未知数进行验证。
解决问题
选自教材第41~42页练习八
1
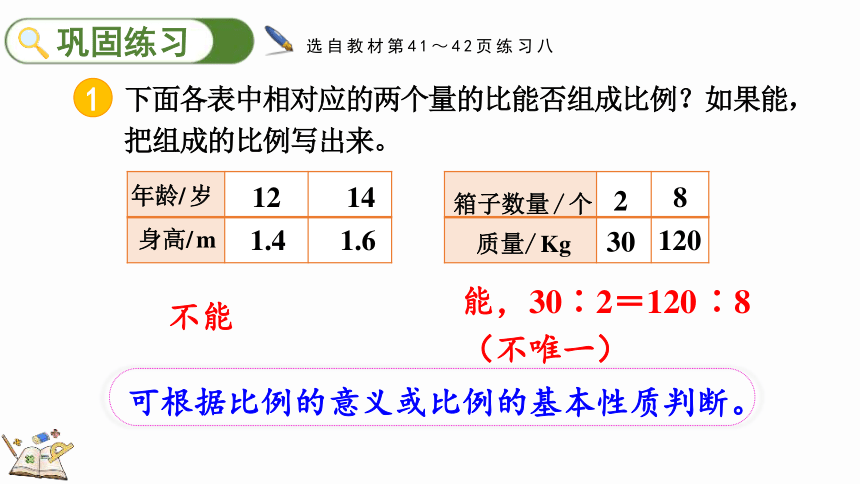
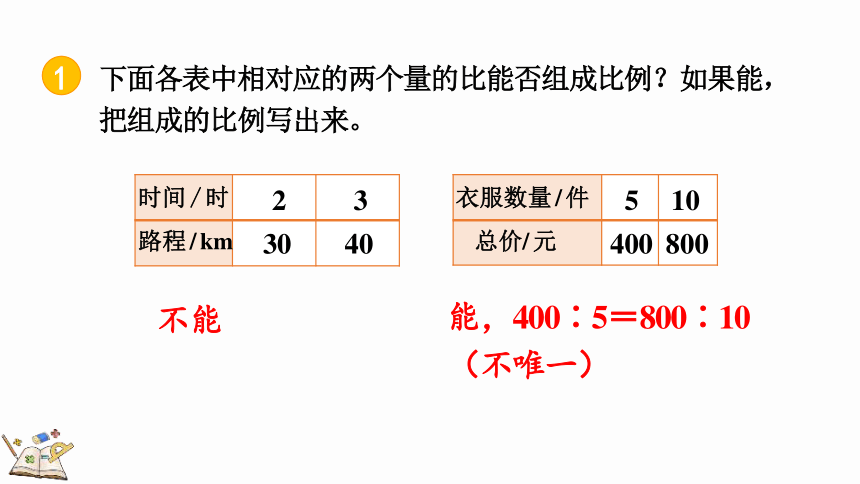
下面各表中相对应的两个量的比能否组成比例?如果能,
把组成的比例写出来。
年龄/岁
12
14
身高/m
1.4
1.6
箱子数量/个
2
8
质量/Kg
30
120
不能
能,30∶2=120∶8(不唯一)
可根据比例的意义或比例的基本性质判断。
1
下面各表中相对应的两个量的比能否组成比例?如果能,
把组成的比例写出来。
时间/时
2
3
路程/km
30
40
衣服数量/件
5
10
总价/元
400
800
不能
能,400∶5=800∶10(不唯一)
2
(1)4,5,12和15
(2)2,3,4和5
(3)1.6,6.4,2和5
下面哪组中的四个数可以组成比例?把组成的比例写出来。
给四个数排序,计算最大数与最小数的积是否等于其他两个数的积,相等即可组成比例。
5×2 ≠ 3×4
不能组成比例
6.4×1.6 ≠ 2×5
不能组成比例
2
(1)4,5,12和15
下面哪组中的四个数可以组成比例?把组成的比例写出来。
15×4=12×5
可以组成比例
4∶5=12∶15
4∶12=5∶15
15∶5=12∶4
15∶12=5∶4
5∶15=4∶12
5∶4=15∶12
12∶15=4∶5
12∶4=15∶5
可以组成比例
(不唯一,共8个)
× = ×
: = :
3
你还能写出哪些与上面不同的呢?
写出比值是5的两个比,并组成比例。
(答案不唯一)
例:5:1 10:2 5:1=10:2
15∶3 20∶4 15∶3=20∶4
4
李叔叔承包了两块水稻田,面积分别为0.5公顷和0.8公
顷。秋收时,两块水稻田的产量分别为3.75 t和6 t。两
块水稻田的产量与面积之比,是否可以组成比例?如果
可以组成比例,指出比例的内项和外项。
3.75∶0.5=7.5 6∶0.8=7.5 可以组成比例。
3.75∶0.5=6∶0.8
6∶0.8=3.75∶0.5
外项
内项
外项
内项
5
判断下面哪组中的两个比可以组成比例。
(2)1.4:2和28:40
不能组成比例
6×12=72
9×9=81
6×12≠9×9
能组成比例
1.4×40=56
2×28=56
1.4×40=2×28
(1)6:9和9:12
5
判断下面哪组中的两个比可以组成比例。
(4)7.5∶1.3和5.7∶3.1
不能组成比例
7.5×3.1=23.25
1.3×5.7=7.41
1.4×40≠1.3×5.7
能组成比例
6
小红说得对吗?
我不运动时心脏45秒跳54次。
那1分钟跳72次。
54∶45=1.2
72∶60=1.2
两个比的比值相等,所以小红说得对。
1分=60秒
运用比例知识,看心跳的次数与相对应时间的比值是否相等。
7
已知24×3=8×9,你能写出比例吗?你能写几个?
24∶8=9∶3 24∶9=8∶3 3∶8=9∶24 3∶9=8∶24
能写8个
8∶24=3∶9 9∶24=3∶8 8∶3=24∶9 9∶3=24∶8
8
解比例。
(2)0.8:4=x:8
4x=0.8×8
x=1.6
8
解比例。
x =3
2x=8×9
x=36
9
相同质量的水和冰的体积之比是9∶10。一块体积是
50 dm3的冰,化成水后的体积是多少?
解:设化成水后的体积是x dm3。
答:化成水后的体积是45 dm3。
x∶50=9∶10
10x=50×9
x=45
根据体积比不变列比例解答。
10
按照下面的条件列出比例,并且解比例。
(1)5与8的比等于40与x的比。
5∶8=40∶x
5x=8×40
x=64
解:
10
按照下面的条件列出比例,并且解比例。
解:
x=
×
x:=
:
x=
10
按照下面的条件列出比例,并且解比例。
(3)比例的两个内项分别是2和5,两个外项分别是x和2.5。
注意:可以列出4个不同的比例,但x 的值是相同的。
2.5∶2=5∶x
2.5x=2×5
x=4
解:
11
汽车厂按1∶20的比生产了一批汽车模型。
(1)轿车模型长24.3 cm,轿车的实际长度是多少?
解:设轿车的实际长度是xcm。
答:轿车的实际长度是486cm。
24.3:x=1:20
x=20×24.3
x=486
汽车模型的长:汽车的实际长度=1∶20
11
汽车厂按1∶20的比生产了一批汽车模型。
(2)公共汽车长11.76 m,公共汽车模型的长度是多少?
解:设公共汽车模型的长度是xcm。
答:公共汽车模型的长度是0.588m。
x:11.76=1:20
20x=11.76×1
x=0.588
12
一个秦代高级军吏俑模型的高度与实际高度的比是1∶10,
模型高度是19.6 cm。这个高级军吏俑的实际高度是多少?
解:设这个高级军吏俑的实际高度是xcm。
答:这个高级军吏俑的实际高度是196cm。
19.6:x=1:10
x=19.6×10
x=196
13
某小区1号楼的实际高度是35 m,与模型高度的比是
50∶1。模型的高度是多少厘米?
35m= 3500cm
解:设模型的高度是xcm。
50:1=3500:x
x=70
答:模型的高度是70cm。
14
把下面的等式改写成比例。
(1)3×40=8×15
3∶8=15∶40 3∶15=8∶40
40∶8=15∶3 40∶15=8∶3
15∶40=3∶8 8∶40=3∶15 15∶3=40∶8 8∶3=40∶15
注意:相乘的两个数要同时作比例的外项和内项。
14
把下面的等式改写成比例。
(2)2.5×0.4=0.5×2
2.5∶0.5=2∶0.4 2.5∶2=0.5∶0.4
0.4∶0.5=2∶2.5 0.4∶2=0.5∶2.5
2∶0.4=2.5∶0.5 0.5∶0.4=2.5∶2 2∶2.5=0.4∶0.5 0.5∶2.5=0.4∶2
15
李老师买了6个足球和8个篮球,买两种球所花钱数相等。
(1)足球与篮球的单价之比是多少?
6×足球的单价=8×篮球的单价
买两种球所花的钱数相等。
足球的单价∶ 篮球的单价=8∶6 =4∶3
答:足球与篮球的单价之比是4∶3。
15
李老师买了6个足球和8个篮球,买两种球所花钱数相等。
(2)足球的单价是40元,篮球的单价是多少?
解:设篮球的单价是x元。
40∶x=4∶3
4x=3×40
答:篮球的单价是30元。
x=30
15
李老师买了6个足球和8个篮球,买两种球所花钱数相等。
(3)你还能提出其他数学问题并解答吗?
(答案不唯一)
例:篮球的单价是36元,足球的单价是多少元?
解:设足球的单价是y元。
y:36=8:6
y=48
答:足球的单价是48元。
1.
(1)有两个比组成的式子叫作比例。 ( )
(2)如果两个比可以组成比例,那么这两个比的比值一定
相等。 ( )
(3)组成比例的两个比一定是最简的整数比。 ( )
√
×
×
判断。
2.
1.5∶4=12∶32,如果第一个比的前项加上2.5,那么第二个比的后项要减去几,这个比例仍然成立?
温馨提示
比例的基本性质
1.5+2.5=4
4×12÷4=12
32-12=20
答:第二个比的后项要减去20,这个比例仍然成立。
变化后第一个比的前项
变化后第二个比的后项
3.
内项可能是哪两个数?
1
48
3
16
4
12
6
8
32∶□ = □∶2
1
64
4
16
8
8
外项
24×2=48
外项
32×2=64
24∶□ = □∶2
这节课有什么收获呢?
比的意义
写比例时要注意前后项的顺序对应。
用字母表示:
a∶b=c∶d(b,d≠0)
或
比例的基本性质:内、外项乘积相等
内项
外项
3 ∶ 9 = 1.2 ∶ 3.6
3×3.6=9×1.2
1.从教材练习八中选取;
2.从课时练中选取。
意义:
解比例:求比例中的未知项
基本性质:
比例
表示两个比相等的式子
两个内项的积等于两个外项的积
第4课时 练习八
第四单元 比例
比例的意义
2.4:1.6=60:40
像这样表示两个比相等的式子叫作比例。
用字母表示:
a∶b=c∶d(b,d≠0)
=
或
比例的各部分名称
组成比例的四个数,叫作比例的项,两端的两项叫作比例的外项,中间的两项叫作比例的内项。
2.4
1.6
60
40
=
内项
内项
外项
外项
比例的基本性质
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
内项
外项
3 ∶ 9 = 1.2 ∶ 3.6
2.4×40=1.6×60
9×1.2=3×3.6
2.4
1.6
60
40
=
内项
内项
外项
外项
ad=bc。
如果 a∶b=c∶d或
a
b
c
d
=
(b、d≠0),
那么
判断两个比能否组成比例
比例的意义
比例的基本性质
一算 算出两个比的比值
二看 看两个比值是否相等
一算 分别算出两个外项积和两个内项积
二看 看两个积是否相等
解比例
先把比例转化成外项乘积与内项乘积相等的形式(即方程)。
解比例的方法:根据比例的基本性质解比例。
再通过解方程求出未知项的值。
解比例
找到隐含的比例关系列出比例。
根据比例的基本性质,先将比相等转化为积相等,再解方程。
对所求未知数进行验证。
解决问题
选自教材第41~42页练习八
1
下面各表中相对应的两个量的比能否组成比例?如果能,
把组成的比例写出来。
年龄/岁
12
14
身高/m
1.4
1.6
箱子数量/个
2
8
质量/Kg
30
120
不能
能,30∶2=120∶8(不唯一)
可根据比例的意义或比例的基本性质判断。
1
下面各表中相对应的两个量的比能否组成比例?如果能,
把组成的比例写出来。
时间/时
2
3
路程/km
30
40
衣服数量/件
5
10
总价/元
400
800
不能
能,400∶5=800∶10(不唯一)
2
(1)4,5,12和15
(2)2,3,4和5
(3)1.6,6.4,2和5
下面哪组中的四个数可以组成比例?把组成的比例写出来。
给四个数排序,计算最大数与最小数的积是否等于其他两个数的积,相等即可组成比例。
5×2 ≠ 3×4
不能组成比例
6.4×1.6 ≠ 2×5
不能组成比例
2
(1)4,5,12和15
下面哪组中的四个数可以组成比例?把组成的比例写出来。
15×4=12×5
可以组成比例
4∶5=12∶15
4∶12=5∶15
15∶5=12∶4
15∶12=5∶4
5∶15=4∶12
5∶4=15∶12
12∶15=4∶5
12∶4=15∶5
可以组成比例
(不唯一,共8个)
× = ×
: = :
3
你还能写出哪些与上面不同的呢?
写出比值是5的两个比,并组成比例。
(答案不唯一)
例:5:1 10:2 5:1=10:2
15∶3 20∶4 15∶3=20∶4
4
李叔叔承包了两块水稻田,面积分别为0.5公顷和0.8公
顷。秋收时,两块水稻田的产量分别为3.75 t和6 t。两
块水稻田的产量与面积之比,是否可以组成比例?如果
可以组成比例,指出比例的内项和外项。
3.75∶0.5=7.5 6∶0.8=7.5 可以组成比例。
3.75∶0.5=6∶0.8
6∶0.8=3.75∶0.5
外项
内项
外项
内项
5
判断下面哪组中的两个比可以组成比例。
(2)1.4:2和28:40
不能组成比例
6×12=72
9×9=81
6×12≠9×9
能组成比例
1.4×40=56
2×28=56
1.4×40=2×28
(1)6:9和9:12
5
判断下面哪组中的两个比可以组成比例。
(4)7.5∶1.3和5.7∶3.1
不能组成比例
7.5×3.1=23.25
1.3×5.7=7.41
1.4×40≠1.3×5.7
能组成比例
6
小红说得对吗?
我不运动时心脏45秒跳54次。
那1分钟跳72次。
54∶45=1.2
72∶60=1.2
两个比的比值相等,所以小红说得对。
1分=60秒
运用比例知识,看心跳的次数与相对应时间的比值是否相等。
7
已知24×3=8×9,你能写出比例吗?你能写几个?
24∶8=9∶3 24∶9=8∶3 3∶8=9∶24 3∶9=8∶24
能写8个
8∶24=3∶9 9∶24=3∶8 8∶3=24∶9 9∶3=24∶8
8
解比例。
(2)0.8:4=x:8
4x=0.8×8
x=1.6
8
解比例。
x =3
2x=8×9
x=36
9
相同质量的水和冰的体积之比是9∶10。一块体积是
50 dm3的冰,化成水后的体积是多少?
解:设化成水后的体积是x dm3。
答:化成水后的体积是45 dm3。
x∶50=9∶10
10x=50×9
x=45
根据体积比不变列比例解答。
10
按照下面的条件列出比例,并且解比例。
(1)5与8的比等于40与x的比。
5∶8=40∶x
5x=8×40
x=64
解:
10
按照下面的条件列出比例,并且解比例。
解:
x=
×
x:=
:
x=
10
按照下面的条件列出比例,并且解比例。
(3)比例的两个内项分别是2和5,两个外项分别是x和2.5。
注意:可以列出4个不同的比例,但x 的值是相同的。
2.5∶2=5∶x
2.5x=2×5
x=4
解:
11
汽车厂按1∶20的比生产了一批汽车模型。
(1)轿车模型长24.3 cm,轿车的实际长度是多少?
解:设轿车的实际长度是xcm。
答:轿车的实际长度是486cm。
24.3:x=1:20
x=20×24.3
x=486
汽车模型的长:汽车的实际长度=1∶20
11
汽车厂按1∶20的比生产了一批汽车模型。
(2)公共汽车长11.76 m,公共汽车模型的长度是多少?
解:设公共汽车模型的长度是xcm。
答:公共汽车模型的长度是0.588m。
x:11.76=1:20
20x=11.76×1
x=0.588
12
一个秦代高级军吏俑模型的高度与实际高度的比是1∶10,
模型高度是19.6 cm。这个高级军吏俑的实际高度是多少?
解:设这个高级军吏俑的实际高度是xcm。
答:这个高级军吏俑的实际高度是196cm。
19.6:x=1:10
x=19.6×10
x=196
13
某小区1号楼的实际高度是35 m,与模型高度的比是
50∶1。模型的高度是多少厘米?
35m= 3500cm
解:设模型的高度是xcm。
50:1=3500:x
x=70
答:模型的高度是70cm。
14
把下面的等式改写成比例。
(1)3×40=8×15
3∶8=15∶40 3∶15=8∶40
40∶8=15∶3 40∶15=8∶3
15∶40=3∶8 8∶40=3∶15 15∶3=40∶8 8∶3=40∶15
注意:相乘的两个数要同时作比例的外项和内项。
14
把下面的等式改写成比例。
(2)2.5×0.4=0.5×2
2.5∶0.5=2∶0.4 2.5∶2=0.5∶0.4
0.4∶0.5=2∶2.5 0.4∶2=0.5∶2.5
2∶0.4=2.5∶0.5 0.5∶0.4=2.5∶2 2∶2.5=0.4∶0.5 0.5∶2.5=0.4∶2
15
李老师买了6个足球和8个篮球,买两种球所花钱数相等。
(1)足球与篮球的单价之比是多少?
6×足球的单价=8×篮球的单价
买两种球所花的钱数相等。
足球的单价∶ 篮球的单价=8∶6 =4∶3
答:足球与篮球的单价之比是4∶3。
15
李老师买了6个足球和8个篮球,买两种球所花钱数相等。
(2)足球的单价是40元,篮球的单价是多少?
解:设篮球的单价是x元。
40∶x=4∶3
4x=3×40
答:篮球的单价是30元。
x=30
15
李老师买了6个足球和8个篮球,买两种球所花钱数相等。
(3)你还能提出其他数学问题并解答吗?
(答案不唯一)
例:篮球的单价是36元,足球的单价是多少元?
解:设足球的单价是y元。
y:36=8:6
y=48
答:足球的单价是48元。
1.
(1)有两个比组成的式子叫作比例。 ( )
(2)如果两个比可以组成比例,那么这两个比的比值一定
相等。 ( )
(3)组成比例的两个比一定是最简的整数比。 ( )
√
×
×
判断。
2.
1.5∶4=12∶32,如果第一个比的前项加上2.5,那么第二个比的后项要减去几,这个比例仍然成立?
温馨提示
比例的基本性质
1.5+2.5=4
4×12÷4=12
32-12=20
答:第二个比的后项要减去20,这个比例仍然成立。
变化后第一个比的前项
变化后第二个比的后项
3.
内项可能是哪两个数?
1
48
3
16
4
12
6
8
32∶□ = □∶2
1
64
4
16
8
8
外项
24×2=48
外项
32×2=64
24∶□ = □∶2
这节课有什么收获呢?
比的意义
写比例时要注意前后项的顺序对应。
用字母表示:
a∶b=c∶d(b,d≠0)
或
比例的基本性质:内、外项乘积相等
内项
外项
3 ∶ 9 = 1.2 ∶ 3.6
3×3.6=9×1.2
1.从教材练习八中选取;
2.从课时练中选取。
意义:
解比例:求比例中的未知项
基本性质:
比例
表示两个比相等的式子
两个内项的积等于两个外项的积
