4.4 整理和复习 课件-人教版数学六年级下册(共27张PPT)
文档属性
| 名称 | 4.4 整理和复习 课件-人教版数学六年级下册(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 00:00:00 | ||
图片预览


文档简介
(共27张PPT)
第四单元 比例
第16课时 整理和复习
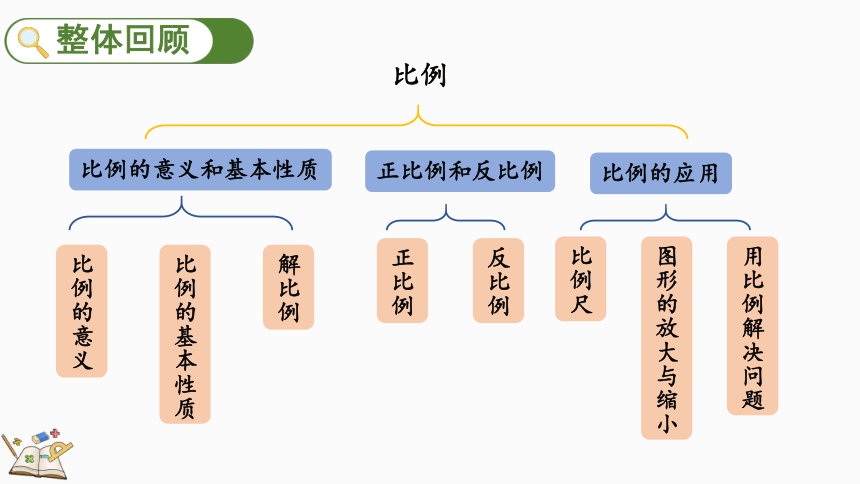
比例
比例的意义和基本性质
比例的应用
比例的意义
比例的基本性质
解比例
比例尺
图形的放大与缩小
正比例和反比例
正比例
反比例
用比例解决问题
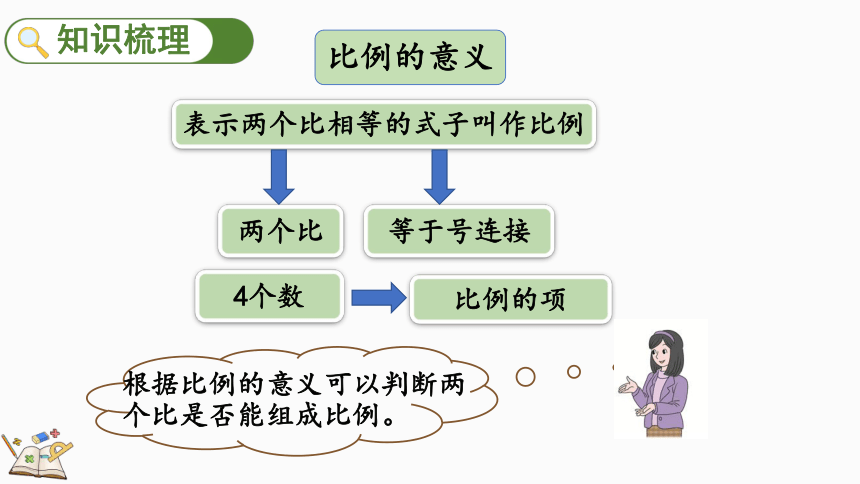
4个数
两个比
表示两个比相等的式子叫作比例
比例的项
等于号连接
根据比例的意义可以判断两个比是否能组成比例。
比例的意义
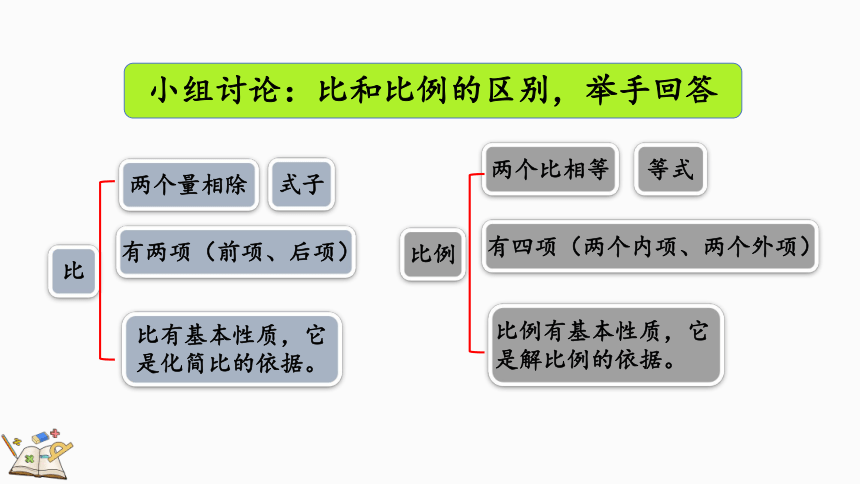
小组讨论:比和比例的区别,举手回答
比
两个量相除
有两项(前项、后项)
比有基本性质,它是化简比的依据。
比例
等式
两个比相等
式子
有四项(两个内项、两个外项)
比例有基本性质,它是解比例的依据。
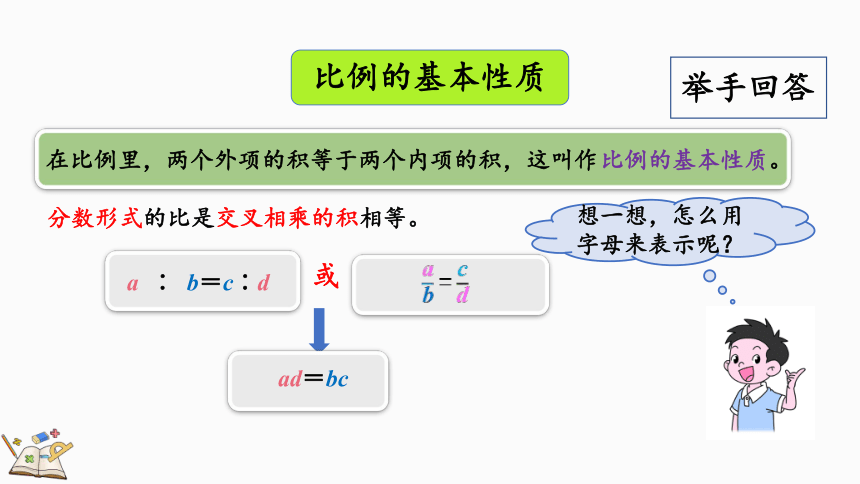
比例的基本性质
在比例里,两个外项的积等于两个内项的积,这叫作
a ∶ b=c∶d
ad=bc
想一想,怎么用字母来表示呢?
分数形式的比是交叉相乘的积相等。
=
或
举手回答
比例的基本性质。
比例的基本性质
解比例
举手回答:解比例依据的是什么?
如果已知比例中的任何三项,就可以求出这个比例中的那个未知项。求比例中的未知项,叫作解比例。
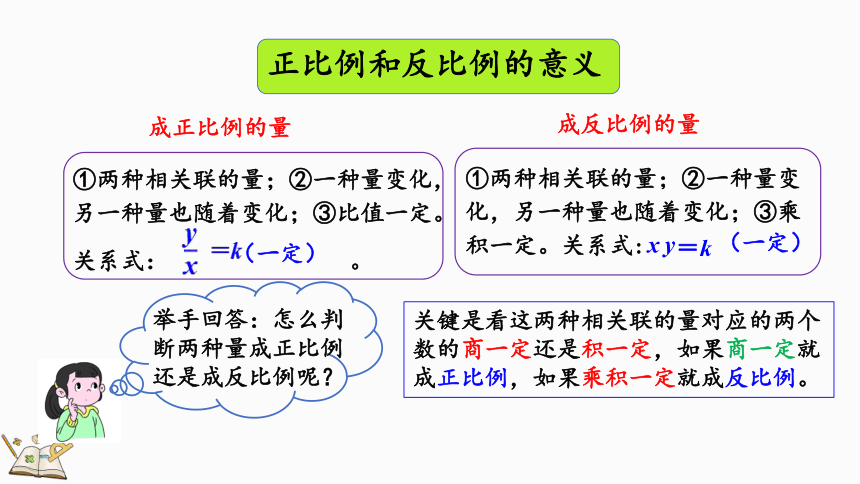
正比例和反比例的意义
成正比例的量
①两种相关联的量;②一种量变化,另一种量也随着变化;③乘积一定。关系式:
y
x
=k
(一定)
关键是看这两种相关联的量对应的两个数的商一定还是积一定,如果商一定就成正比例,如果乘积一定就成反比例。
举手回答:怎么判断两种量成正比例还是成反比例呢?
成反比例的量
①两种相关联的量;②一种量变化,另一种量也随着变化;③比值一定。
关系式: 。
=k
(一定)
一幅图的图上距离和实际距离的比。
比例尺
比例尺的分类
(1)按表现形式,可以分为数值比例尺和线段比例尺。
(2)按将实际距离放大还是缩小,可以分为缩小比例尺和放大比例尺。
应用比例尺画图
(3)画图
(4)标出实际距离和比例尺
(1)确定比例尺
(2)根据比例尺求出图上距离
比例尺的意义
一看、二算、三画。
图形的放大与缩小的特点
形状相同,大小不同。
图形的放大与缩小
图形的放大与缩小的方法
用比例解决问题
根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例,根据正反比例关系式列出方法并求解。
两个数相除又叫作两个数的比。
表示两个比相等的式子叫作比例。
选自教材第63页整理和复习第1~4题
1
比 比例
联系 比例是由两个比值相等的比组成的 区别 意义 表示两个数相除 表示两个比相等的式子
各部分 名称
基本性质 比的前项和后项同时乘或除以相同的数 (0除外),比值不变 在比例里,两个外项的积等于两个内项的积
2.4∶1.6=1.5
前项
比号
后项
比值
2.4∶1.6=60∶40
外项
内项
说一说:什么是比?什么是比例?比和比例有什么联系和区别?
2
解比例的依据是什么?解下面的比例。
∶∶4
依据:比例的基本性质。
解:5x4×6
解:4×
2
解比例的依据是什么?解下面的比例。
依据:比例的基本性质。
6.5∶x3.25∶4
解:1.2x2.5×3
解: 3.25x6.5×4
x8
3
下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
(1)从甲地到乙地的路程是240 km,汽车行驶的速度与时间如下表。
速度/(千米/时)
时间/时
40
6
50
4.8
60
4
80
3
100
2.4
因为行驶速度×行驶时间=路程(一定),所以行驶速度和行驶时间成反比例关系。
3
(2)圆锥的高是30 cm,它的底面积与体积如下表。
底面积/cm2
体积/cm3
5
50
8
80
10
100
16
160
20
200
所以圆锥的底面积与体积成正比例关系。
下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
因为=×圆锥的高=10(一定),
3
(3)圆的半径与面积如下表。
半径/cm
面积/cm2
1
π
2
4π
3
9π
4
16π
5
25π
下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
因为=π×圆的半径(不一定),所以圆的面积与圆的半径不成比例关系。
4
(1)李叔叔开车从甲地到乙地,前2小时行驶了100 km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
=
x
3
100
2
2x=100×3
x=
100×3
2
x=150
解:设甲乙两地相距 x km。
答:甲乙两地相距 150 km。
速度一定,路程与时间成正比例关系。
4
(2)李叔叔开车从甲地到乙地一共用了3小时,每小时行驶 50 km。原路返回时每小时行驶60 km,返回时用了多长时间?
路程一定,速度与时间成反比例关系。
60x=50×3
x=
50×3
60
x=2.5
解:设返回时用了x小时。
答:返回时用了2.5小时。
(1)如果a=—,那么当( )一定时,( )和( )成正比例。当( )一定时,( )和( )成反比例。
b
c
b
c
a
a
b
c
1.填空。
a=
b
c
c=ab
b=
a
c
商一定,成正比例;积一定,成反比例。
(2)小圆的半径是2厘米,大圆的半径是3厘米,大圆和小圆的周长比是( )。
C= 2 π r
2π是定值
周长的比=半径的比
3∶2
注意写的顺序哦!
1.填空。
(3)甲、乙两数的比是5∶3,乙数是60,甲数是( )。
100
甲占5份,乙占3份
数量
份数
? —— 1
60 —— 3
乙数
60÷3×5=100
1.填空。
(4)把正方形的边长按1︰2缩小后,周长缩小为原来的( ),面积缩小为原来的( )。
把一个图形按x︰1放大,就是将这个图形的各条边放大x倍。
正方形周长=边长×4
正方形面积=边长×边长
面积与边长的平方有关。
周长与边长有关。
1.填空。
1
4
1
2
把一个图形按1︰x缩小,就是将这个图形的各条边缩小到原来的 。
1
x
2.两地之间的实际距离约为240千米,在一幅图上,两地之间的距离为80厘米,这幅图的比例尺是多少?用线段比例尺怎么表示?
240千米=24000000厘米
80:24000000=1:300000
答:这幅宣传图的比例尺为1:300000。
0
3
6
9km
3.甲、乙两人进行百米赛跑,当甲到达终点时,乙在甲后面20米,如果两人各自的速度不变,要使甲、乙同时到达终点,甲的起跑线应该比原来后移多少米?
画线段图分析一下吧!
甲
乙
100米
100-20=80米
甲
x
(100+x)米
乙
100米
时间一定,速度与路程成正比例。
甲跑的路程:甲的速度=乙跑的路程:乙的速度
甲跑的路程:乙跑的路程=甲的速度:乙的速度
解:设甲的起跑线应该比原来后移x米。
(100+x):100 = 100:(100-20)
80x = 2000
x = 25
答:甲的起跑线应该比原来后移25米。
3.甲、乙两人进行百米赛跑,当甲到达终点时,乙在甲后面20米,如果两人各自的速度不变,要使甲、乙同时到达终点,甲的起跑线应该比原来后移多少米?
1.从教材整理和复习中选取;
2.从课时练中选取。
比例
比例的意义和基本性质
比例的应用
比例的意义
比例的基本性质
解比例
比例尺
图形的放大与缩小
正比例和反比例
正比例
反比例
用比例解决问题
第四单元 比例
第16课时 整理和复习
比例
比例的意义和基本性质
比例的应用
比例的意义
比例的基本性质
解比例
比例尺
图形的放大与缩小
正比例和反比例
正比例
反比例
用比例解决问题
4个数
两个比
表示两个比相等的式子叫作比例
比例的项
等于号连接
根据比例的意义可以判断两个比是否能组成比例。
比例的意义
小组讨论:比和比例的区别,举手回答
比
两个量相除
有两项(前项、后项)
比有基本性质,它是化简比的依据。
比例
等式
两个比相等
式子
有四项(两个内项、两个外项)
比例有基本性质,它是解比例的依据。
比例的基本性质
在比例里,两个外项的积等于两个内项的积,这叫作
a ∶ b=c∶d
ad=bc
想一想,怎么用字母来表示呢?
分数形式的比是交叉相乘的积相等。
=
或
举手回答
比例的基本性质。
比例的基本性质
解比例
举手回答:解比例依据的是什么?
如果已知比例中的任何三项,就可以求出这个比例中的那个未知项。求比例中的未知项,叫作解比例。
正比例和反比例的意义
成正比例的量
①两种相关联的量;②一种量变化,另一种量也随着变化;③乘积一定。关系式:
y
x
=k
(一定)
关键是看这两种相关联的量对应的两个数的商一定还是积一定,如果商一定就成正比例,如果乘积一定就成反比例。
举手回答:怎么判断两种量成正比例还是成反比例呢?
成反比例的量
①两种相关联的量;②一种量变化,另一种量也随着变化;③比值一定。
关系式: 。
=k
(一定)
一幅图的图上距离和实际距离的比。
比例尺
比例尺的分类
(1)按表现形式,可以分为数值比例尺和线段比例尺。
(2)按将实际距离放大还是缩小,可以分为缩小比例尺和放大比例尺。
应用比例尺画图
(3)画图
(4)标出实际距离和比例尺
(1)确定比例尺
(2)根据比例尺求出图上距离
比例尺的意义
一看、二算、三画。
图形的放大与缩小的特点
形状相同,大小不同。
图形的放大与缩小
图形的放大与缩小的方法
用比例解决问题
根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例,根据正反比例关系式列出方法并求解。
两个数相除又叫作两个数的比。
表示两个比相等的式子叫作比例。
选自教材第63页整理和复习第1~4题
1
比 比例
联系 比例是由两个比值相等的比组成的 区别 意义 表示两个数相除 表示两个比相等的式子
各部分 名称
基本性质 比的前项和后项同时乘或除以相同的数 (0除外),比值不变 在比例里,两个外项的积等于两个内项的积
2.4∶1.6=1.5
前项
比号
后项
比值
2.4∶1.6=60∶40
外项
内项
说一说:什么是比?什么是比例?比和比例有什么联系和区别?
2
解比例的依据是什么?解下面的比例。
∶∶4
依据:比例的基本性质。
解:5x4×6
解:4×
2
解比例的依据是什么?解下面的比例。
依据:比例的基本性质。
6.5∶x3.25∶4
解:1.2x2.5×3
解: 3.25x6.5×4
x8
3
下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
(1)从甲地到乙地的路程是240 km,汽车行驶的速度与时间如下表。
速度/(千米/时)
时间/时
40
6
50
4.8
60
4
80
3
100
2.4
因为行驶速度×行驶时间=路程(一定),所以行驶速度和行驶时间成反比例关系。
3
(2)圆锥的高是30 cm,它的底面积与体积如下表。
底面积/cm2
体积/cm3
5
50
8
80
10
100
16
160
20
200
所以圆锥的底面积与体积成正比例关系。
下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
因为=×圆锥的高=10(一定),
3
(3)圆的半径与面积如下表。
半径/cm
面积/cm2
1
π
2
4π
3
9π
4
16π
5
25π
下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
因为=π×圆的半径(不一定),所以圆的面积与圆的半径不成比例关系。
4
(1)李叔叔开车从甲地到乙地,前2小时行驶了100 km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
=
x
3
100
2
2x=100×3
x=
100×3
2
x=150
解:设甲乙两地相距 x km。
答:甲乙两地相距 150 km。
速度一定,路程与时间成正比例关系。
4
(2)李叔叔开车从甲地到乙地一共用了3小时,每小时行驶 50 km。原路返回时每小时行驶60 km,返回时用了多长时间?
路程一定,速度与时间成反比例关系。
60x=50×3
x=
50×3
60
x=2.5
解:设返回时用了x小时。
答:返回时用了2.5小时。
(1)如果a=—,那么当( )一定时,( )和( )成正比例。当( )一定时,( )和( )成反比例。
b
c
b
c
a
a
b
c
1.填空。
a=
b
c
c=ab
b=
a
c
商一定,成正比例;积一定,成反比例。
(2)小圆的半径是2厘米,大圆的半径是3厘米,大圆和小圆的周长比是( )。
C= 2 π r
2π是定值
周长的比=半径的比
3∶2
注意写的顺序哦!
1.填空。
(3)甲、乙两数的比是5∶3,乙数是60,甲数是( )。
100
甲占5份,乙占3份
数量
份数
? —— 1
60 —— 3
乙数
60÷3×5=100
1.填空。
(4)把正方形的边长按1︰2缩小后,周长缩小为原来的( ),面积缩小为原来的( )。
把一个图形按x︰1放大,就是将这个图形的各条边放大x倍。
正方形周长=边长×4
正方形面积=边长×边长
面积与边长的平方有关。
周长与边长有关。
1.填空。
1
4
1
2
把一个图形按1︰x缩小,就是将这个图形的各条边缩小到原来的 。
1
x
2.两地之间的实际距离约为240千米,在一幅图上,两地之间的距离为80厘米,这幅图的比例尺是多少?用线段比例尺怎么表示?
240千米=24000000厘米
80:24000000=1:300000
答:这幅宣传图的比例尺为1:300000。
0
3
6
9km
3.甲、乙两人进行百米赛跑,当甲到达终点时,乙在甲后面20米,如果两人各自的速度不变,要使甲、乙同时到达终点,甲的起跑线应该比原来后移多少米?
画线段图分析一下吧!
甲
乙
100米
100-20=80米
甲
x
(100+x)米
乙
100米
时间一定,速度与路程成正比例。
甲跑的路程:甲的速度=乙跑的路程:乙的速度
甲跑的路程:乙跑的路程=甲的速度:乙的速度
解:设甲的起跑线应该比原来后移x米。
(100+x):100 = 100:(100-20)
80x = 2000
x = 25
答:甲的起跑线应该比原来后移25米。
3.甲、乙两人进行百米赛跑,当甲到达终点时,乙在甲后面20米,如果两人各自的速度不变,要使甲、乙同时到达终点,甲的起跑线应该比原来后移多少米?
1.从教材整理和复习中选取;
2.从课时练中选取。
比例
比例的意义和基本性质
比例的应用
比例的意义
比例的基本性质
解比例
比例尺
图形的放大与缩小
正比例和反比例
正比例
反比例
用比例解决问题
