4.1.2 比例的基本性质 课件-人教版数学六年级下册(共22张PPT)
文档属性
| 名称 | 4.1.2 比例的基本性质 课件-人教版数学六年级下册(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
第2课时 比例的基本性质
第四单元 比例
下面的两个比可以组成比例吗?
比例的每个数都叫什么呢?
3.6∶6和1.2∶2
=0.6
=0.6
3.6:6=1.2:2
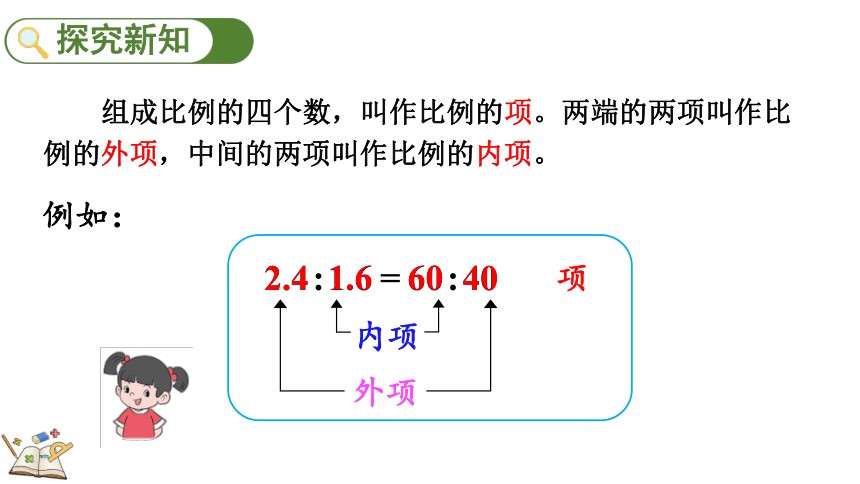
组成比例的四个数,叫作比例的项。两端的两项叫作比例的外项,中间的两项叫作比例的内项。
2.4:1.6=60:40
例如:
外项
内项
2.4
1.6
60
40
项
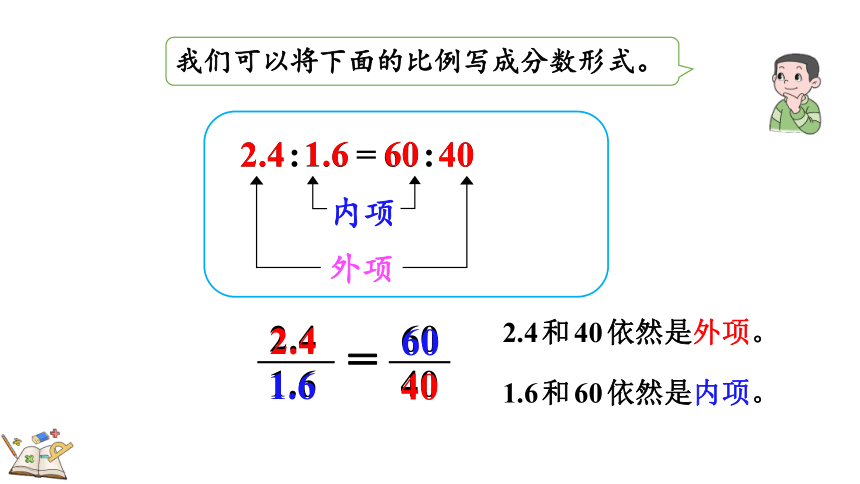
我们可以将下面的比例写成分数形式。
2.4:1.6=60:40
外项
内项
2.4
1.6
60
40
2.4
1.6
60
40
=
2.4和40依然是外项。
1.6和60依然是内项。
2.4
1.6
60
40
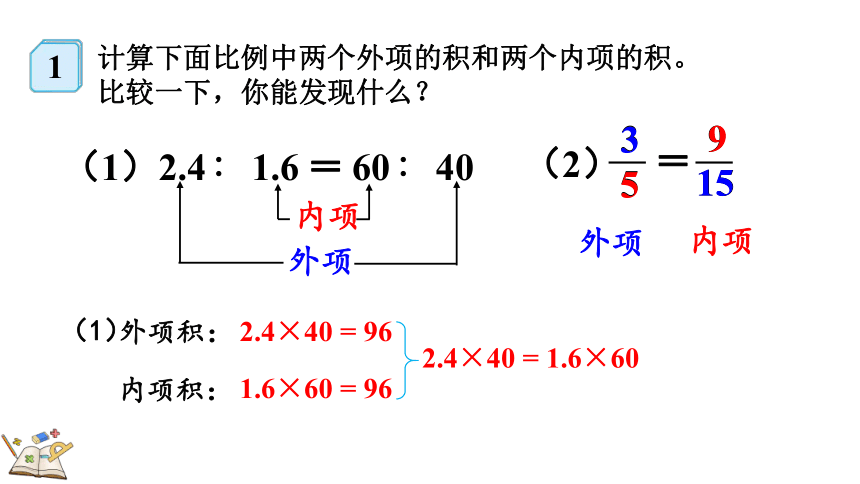
计算下面比例中两个外项的积和两个内项的积。比较一下,你能发现什么?
3
5
9
15
=
(2)
(1)2.4∶1.6=60∶40
3
15
5
9
内项
外项
内项
外项
1
外项积:
内项积:
2.4×40=96
1.6×60=96
2.4×40=1.6×60
(1)
3
5
9
15
=
(2)
(1)2.4∶1.6=60∶40
3
15
5
9
内项
外项
内项
外项
3×15=45
5×9=45
外项积:
内项积:
(2)
3×15=5×9
发现:两个外项的积等于两个内项的积。
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
你能举一个例子,验证你的发现吗?
举例:
80:4=100:5
80:20=24:6
80×5=4×100
80×6=20×24
10×14=7×20
你能用字母表示这个性质吗?
ad=bc。
如果 a∶b=c∶d或
a
b
c
d
=
(b、d≠0),
那么
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
四个不为0的数,如果其中两个数的乘积和另外两个数的乘积相等,这四个数就可以组成比例。
可以运用比例的基本性质判断比例是否成立。
试判断:0.2∶2.5和8∶100
0.2×100=2.5×8
比例成立。
比和比例有什么区别与联系呢?
区别
联系
比
比例
意义
项数
形式
基本性质
2项
表示两个数相除
比是一个除法算式
4项
表示两个比相等
比是一个等式
比的前项和后项同时乘或除以同一个数(0除外),比值不变
在比例里,两个外项的积等于两个内项的积
表示两个比相等的式子就是比例
有几种判断比例是否成立的方法?
小组讨论
在小组内说说自己的想法。
你有几种方法来判断比例是否成立?
小组讨论
有两种方法:首先是看比值是否相等。还可以运用比例的基本性质判断。看其中两个数的乘积和另外两个数的乘积是否相等。
选自教材第39页做一做
1
判断下面哪组中的两个比可以组成比例。
(1)6∶3和8∶5
(2)0.2∶2.5和4∶50
6×5=30
3×8=24
6×5≠3×8
不能组成比例。
0.2×50=10
2.5×4=10
0.2×50=2.5×4
能组成比例。
1
选自教材第39页做一做
判断下面哪组中的两个比可以组成比例。
能组成比例。
不能组成比例。
1.2×5=6
1.
用两种方法判断14∶21和6∶9能否组成比例。
绿色圃中小学教育网http://www.Lspjy.com
14∶21=
6∶9=
=
这两个比能组成比例
14∶21=6∶9
方法二:比例的基本性质
14×9=126 21×6=126
126 = 126
这两个比能组成比例
14∶21=6∶9
方法一:比例的意义
2
3
2
3
2.
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,两块水稻田的产量分别为3.75t和6t。两块水稻田的产量与面积之比,是否可以组成比例?如果可以组成比例,指出比例的内项和外项。
3.75∶0.5=6∶0.8
?
0.5×6=3
0.8×3.75=3
答:两块水稻田的产量与面积之比相等,可以组成比例。
2.
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,两块水稻田的产量分别为3.75t和6t。两块水稻田的产量与面积之比,是否可以组成比例?如果可以组成比例,指出比例的内项和外项。
3.75∶0.5=6∶0.8
内项
外项
4∶5=12∶15,如果内项5增加5,那么外项4应该增加多少才能使比例成立?
(4+x)∶(5+5)=12∶15
(4+x)∶10=12∶15
15(4+x)=12×10
解:设外项4应该增加x才能使比例成立。
15x=60
x=4
答:外项4应该增加4才能使比例成立。
这节课有什么收获呢?
比例的基本性质
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。它是判定两个比能否组成比例的另一个重要依据。
“比例”一词最早出现在古希腊数学家欧多克索斯的著作中,他在其中研究了三角形的比例关系。在欧多克索斯之后,许多古代数学家也研究了比例,如毕达哥拉斯、欧几里得等人。在中世纪时期, 阿拉伯数学家将欧几里得的著作翻译成阿拉伯语, 并对其中的比例问题进行了深入研究。在现代数学中,“比例”是一个非常基础和重要的概念, 被广泛应用于各个领域,如代数、几何、物理、化学等。
比例一词的来历
1.教材第41页练习八第2题;
2.从课时练中选取。
比例的基本性质
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
比例各部分名称:
外项积:
内项积:
2.4×40=96
1.6×60=96
2.4×40=1.6×60
第2课时 比例的基本性质
第四单元 比例
下面的两个比可以组成比例吗?
比例的每个数都叫什么呢?
3.6∶6和1.2∶2
=0.6
=0.6
3.6:6=1.2:2
组成比例的四个数,叫作比例的项。两端的两项叫作比例的外项,中间的两项叫作比例的内项。
2.4:1.6=60:40
例如:
外项
内项
2.4
1.6
60
40
项
我们可以将下面的比例写成分数形式。
2.4:1.6=60:40
外项
内项
2.4
1.6
60
40
2.4
1.6
60
40
=
2.4和40依然是外项。
1.6和60依然是内项。
2.4
1.6
60
40
计算下面比例中两个外项的积和两个内项的积。比较一下,你能发现什么?
3
5
9
15
=
(2)
(1)2.4∶1.6=60∶40
3
15
5
9
内项
外项
内项
外项
1
外项积:
内项积:
2.4×40=96
1.6×60=96
2.4×40=1.6×60
(1)
3
5
9
15
=
(2)
(1)2.4∶1.6=60∶40
3
15
5
9
内项
外项
内项
外项
3×15=45
5×9=45
外项积:
内项积:
(2)
3×15=5×9
发现:两个外项的积等于两个内项的积。
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
你能举一个例子,验证你的发现吗?
举例:
80:4=100:5
80:20=24:6
80×5=4×100
80×6=20×24
10×14=7×20
你能用字母表示这个性质吗?
ad=bc。
如果 a∶b=c∶d或
a
b
c
d
=
(b、d≠0),
那么
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
四个不为0的数,如果其中两个数的乘积和另外两个数的乘积相等,这四个数就可以组成比例。
可以运用比例的基本性质判断比例是否成立。
试判断:0.2∶2.5和8∶100
0.2×100=2.5×8
比例成立。
比和比例有什么区别与联系呢?
区别
联系
比
比例
意义
项数
形式
基本性质
2项
表示两个数相除
比是一个除法算式
4项
表示两个比相等
比是一个等式
比的前项和后项同时乘或除以同一个数(0除外),比值不变
在比例里,两个外项的积等于两个内项的积
表示两个比相等的式子就是比例
有几种判断比例是否成立的方法?
小组讨论
在小组内说说自己的想法。
你有几种方法来判断比例是否成立?
小组讨论
有两种方法:首先是看比值是否相等。还可以运用比例的基本性质判断。看其中两个数的乘积和另外两个数的乘积是否相等。
选自教材第39页做一做
1
判断下面哪组中的两个比可以组成比例。
(1)6∶3和8∶5
(2)0.2∶2.5和4∶50
6×5=30
3×8=24
6×5≠3×8
不能组成比例。
0.2×50=10
2.5×4=10
0.2×50=2.5×4
能组成比例。
1
选自教材第39页做一做
判断下面哪组中的两个比可以组成比例。
能组成比例。
不能组成比例。
1.2×5=6
1.
用两种方法判断14∶21和6∶9能否组成比例。
绿色圃中小学教育网http://www.Lspjy.com
14∶21=
6∶9=
=
这两个比能组成比例
14∶21=6∶9
方法二:比例的基本性质
14×9=126 21×6=126
126 = 126
这两个比能组成比例
14∶21=6∶9
方法一:比例的意义
2
3
2
3
2.
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,两块水稻田的产量分别为3.75t和6t。两块水稻田的产量与面积之比,是否可以组成比例?如果可以组成比例,指出比例的内项和外项。
3.75∶0.5=6∶0.8
?
0.5×6=3
0.8×3.75=3
答:两块水稻田的产量与面积之比相等,可以组成比例。
2.
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,两块水稻田的产量分别为3.75t和6t。两块水稻田的产量与面积之比,是否可以组成比例?如果可以组成比例,指出比例的内项和外项。
3.75∶0.5=6∶0.8
内项
外项
4∶5=12∶15,如果内项5增加5,那么外项4应该增加多少才能使比例成立?
(4+x)∶(5+5)=12∶15
(4+x)∶10=12∶15
15(4+x)=12×10
解:设外项4应该增加x才能使比例成立。
15x=60
x=4
答:外项4应该增加4才能使比例成立。
这节课有什么收获呢?
比例的基本性质
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。它是判定两个比能否组成比例的另一个重要依据。
“比例”一词最早出现在古希腊数学家欧多克索斯的著作中,他在其中研究了三角形的比例关系。在欧多克索斯之后,许多古代数学家也研究了比例,如毕达哥拉斯、欧几里得等人。在中世纪时期, 阿拉伯数学家将欧几里得的著作翻译成阿拉伯语, 并对其中的比例问题进行了深入研究。在现代数学中,“比例”是一个非常基础和重要的概念, 被广泛应用于各个领域,如代数、几何、物理、化学等。
比例一词的来历
1.教材第41页练习八第2题;
2.从课时练中选取。
比例的基本性质
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
比例各部分名称:
外项积:
内项积:
2.4×40=96
1.6×60=96
2.4×40=1.6×60
