鲁教版七年级数学下册第10章10.3直角三角形测试题(含答案)
文档属性
| 名称 | 鲁教版七年级数学下册第10章10.3直角三角形测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 112.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-10 00:00:00 | ||
图片预览


文档简介
鲁教版七年级数学下册第10章10.3直角三角形测试题(含答案)
一.选择题(共10小题)
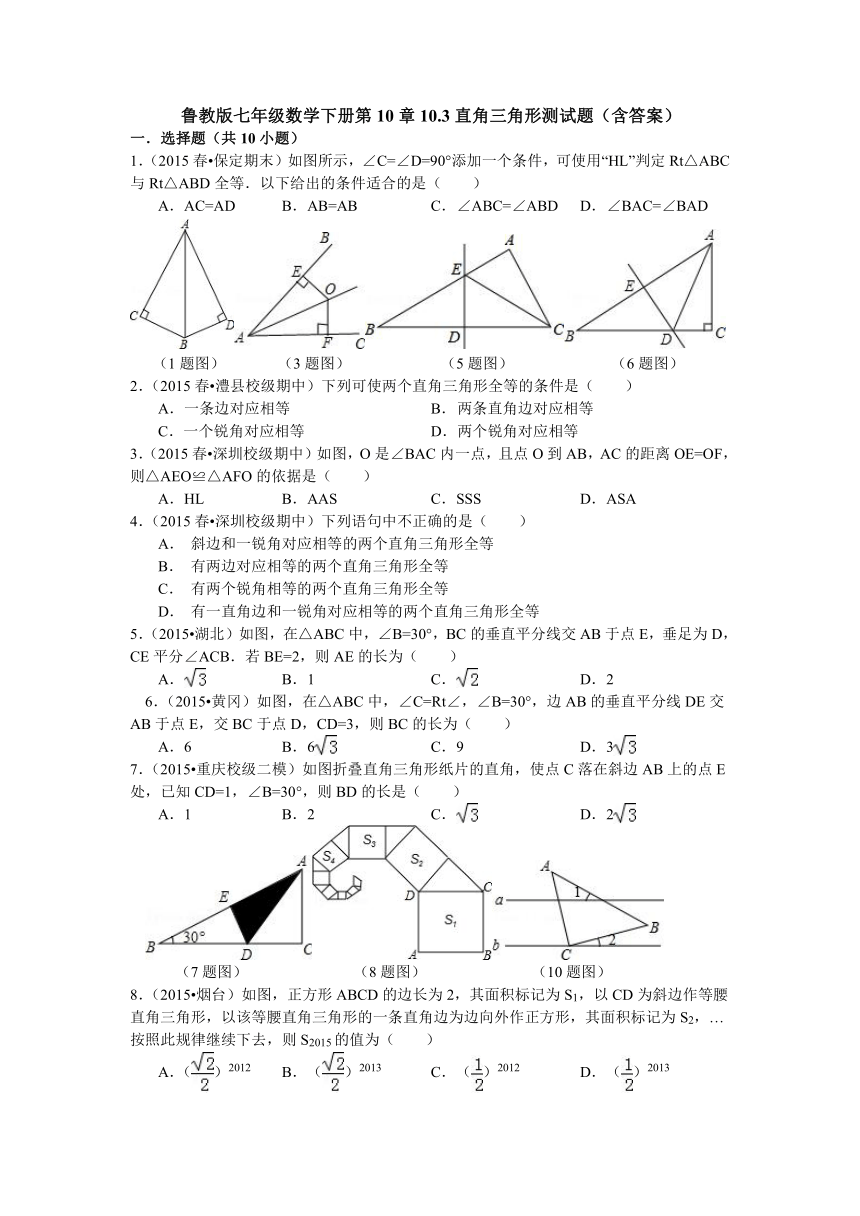
1.(2015春 保定期末)如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B. AB=AB C. ∠ABC=∠ABD D. ∠BAC=∠BAD
(1题图) (3题图) (5题图) (6题图)
2.(2015春 澧县校级期中)下列可使两个直角三角形全等的条件是( )
A.一条边对应相等 B. 两条直角边对应相等
C.一个锐角对应相等 D. 两个锐角对应相等
3.(2015春 深圳校级期中)如图,O是∠BAC内一点,且点O到AB,AC的距离OE=OF,则△AEO≌△AFO的依据是( )
A.HL B. AAS C. SSS D. ASA
4.(2015春 深圳校级期中)下列语句中不正确的是( )
A. 斜边和一锐角对应相等的两个直角三角形全等
B. 有两边对应相等的两个直角三角形全等
C. 有两个锐角相等的两个直角三角形全等
D. 有一直角边和一锐角对应相等的两个直角三角形全等
5.(2015 湖北)如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
A. B. 1 C. D. 2
6.(2015 黄冈)如图,在△ABC中,∠C=Rt∠,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
A.6 B. 6 C. 9 D. 3
7.(2015 重庆校级二模)如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
A.1 B. 2 C. D. 2
(7题图) (8题图) (10题图)
8.(2015 烟台)如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( )
A.()2012 B. ()2013 C. ()2012 D. ()2013
9.(2015春 荆门月考)两块能完全重合的两张等腰直角三角形纸片能拼成下列图形:①平行四边形(不包括菱形、矩形、正方形),②矩形,③正方形,④等边三角形,⑤等腰直角三角形( )
A.①③⑤ B. ②③⑤ C. ①②③ D. ①③④⑤
10.(2015春 罗田县期中)直线a∥b,等腰直角三角形ABC直角顶点C在直线b上,若∠1=20°,则∠2=( )
A.25° B. 30° C. 20° D. 35°
二.填空题(共5小题)
11.(2015 毕节市)如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD= .
(11题图) (12题图) (13题图) (14题图)
12.(2015 曲靖)如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
13.(2015 伊春模拟)某市在旧城改造中,计划在市内一块如图所示三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要 .
14.(2014秋 岑溪市期中)如图所示,∠B=∠D=90°,要使△ABC≌△ADC,还需添加一个条件,这个条件可以是 (只需填一个即可)
15.(2015春 株洲校级期中)边长为2,2,2的三角形是 三角形.
三.解答题(共5小题)
16.(2015春 澧县校级期中)如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
17.(2014 大连三模)如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于点E.
求证:AD=BE.
18.(2014 顺义区一模)如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,BC=4,CD=3,求AB的长.
19.(2014秋 龙口市期末)如图,在△ABC中,∠C=90°,AD平分∠CAB交CB于点D,过点D作DE⊥AB于点E,若∠B=30°,CD=5.
(1)求BD的长;
(2)AE与BE相等吗?说明理由.
20.(2014秋 黔东南州期末)已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)求证:AD和CE垂直.
鲁教版七年级数学下册第10章10.3直角三角形测试题参考答案
一.选择题(共10小题)
1.A.2.B.3.A.4.C.5.B.6.C.7.B.8.C.9.A.10.A.
二.填空题(共5小题)
11. 2 .12.(6+2)a .13. 150a元 .14. AB=AD 15. 等腰直角
三.解答题(共5小题)
16.证明:(1)在△ABC和△DCB中,∠A=∠D=90°,AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形
∵Rt△ABC≌Rt△DCB∴∠ACB=∠DCB∴OB=OC∴△OBC是等腰三角形
17.证明:∵AD∥BC,∴∠ADB=∠DBC.
∵CE⊥BD,∴∠BEC=90°.
∵∠A=90°,∴∠A=∠BEC.
∵BD=BC,∴△ABD≌△BCE.∴AD=BE.
18.解:延长DA,CB,交于点E,∵∠ABE=∠D=90°,∠C=60°∴∠E=30°,
在Rt△DCE中∵CD=3,∴CE=6;∵BC=4,所以BE=2。
设AB=x,则有AE=2x,根据勾股定理得:x2+22=(2x)2,
解得:x=,
(18题图) (20题图)
19.解:(1)∵AD平分∠CAB,∠C=90°,DE⊥AB,∴CD=DE=5,
∵∠B=30°,∴BD=2DE=10,
(2)AE与BE相等,理由如下:
∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°,
∵AD平分∠CAB交CB于点D,∴∠DAB=30°,∴AD=BD,
∵DE⊥AB,∴AE=BE.
20.证明:(1)∵△ABC和△DBE均为等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,即∠ABD=∠CBE,
∴△ABD≌△CBE,∴AD=CE.
(2)延长AD分别交BC和CE于G和F,
∵△ABD≌△CBE,
∴∠BAD=∠BCE,
∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°,
又∵∠BGA=∠CGF,
∴∠AFC=∠ABC=90°,
∴AD⊥CE.
一.选择题(共10小题)
1.(2015春 保定期末)如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B. AB=AB C. ∠ABC=∠ABD D. ∠BAC=∠BAD
(1题图) (3题图) (5题图) (6题图)
2.(2015春 澧县校级期中)下列可使两个直角三角形全等的条件是( )
A.一条边对应相等 B. 两条直角边对应相等
C.一个锐角对应相等 D. 两个锐角对应相等
3.(2015春 深圳校级期中)如图,O是∠BAC内一点,且点O到AB,AC的距离OE=OF,则△AEO≌△AFO的依据是( )
A.HL B. AAS C. SSS D. ASA
4.(2015春 深圳校级期中)下列语句中不正确的是( )
A. 斜边和一锐角对应相等的两个直角三角形全等
B. 有两边对应相等的两个直角三角形全等
C. 有两个锐角相等的两个直角三角形全等
D. 有一直角边和一锐角对应相等的两个直角三角形全等
5.(2015 湖北)如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
A. B. 1 C. D. 2
6.(2015 黄冈)如图,在△ABC中,∠C=Rt∠,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
A.6 B. 6 C. 9 D. 3
7.(2015 重庆校级二模)如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
A.1 B. 2 C. D. 2
(7题图) (8题图) (10题图)
8.(2015 烟台)如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( )
A.()2012 B. ()2013 C. ()2012 D. ()2013
9.(2015春 荆门月考)两块能完全重合的两张等腰直角三角形纸片能拼成下列图形:①平行四边形(不包括菱形、矩形、正方形),②矩形,③正方形,④等边三角形,⑤等腰直角三角形( )
A.①③⑤ B. ②③⑤ C. ①②③ D. ①③④⑤
10.(2015春 罗田县期中)直线a∥b,等腰直角三角形ABC直角顶点C在直线b上,若∠1=20°,则∠2=( )
A.25° B. 30° C. 20° D. 35°
二.填空题(共5小题)
11.(2015 毕节市)如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD= .
(11题图) (12题图) (13题图) (14题图)
12.(2015 曲靖)如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
13.(2015 伊春模拟)某市在旧城改造中,计划在市内一块如图所示三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要 .
14.(2014秋 岑溪市期中)如图所示,∠B=∠D=90°,要使△ABC≌△ADC,还需添加一个条件,这个条件可以是 (只需填一个即可)
15.(2015春 株洲校级期中)边长为2,2,2的三角形是 三角形.
三.解答题(共5小题)
16.(2015春 澧县校级期中)如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
17.(2014 大连三模)如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于点E.
求证:AD=BE.
18.(2014 顺义区一模)如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,BC=4,CD=3,求AB的长.
19.(2014秋 龙口市期末)如图,在△ABC中,∠C=90°,AD平分∠CAB交CB于点D,过点D作DE⊥AB于点E,若∠B=30°,CD=5.
(1)求BD的长;
(2)AE与BE相等吗?说明理由.
20.(2014秋 黔东南州期末)已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)求证:AD和CE垂直.
鲁教版七年级数学下册第10章10.3直角三角形测试题参考答案
一.选择题(共10小题)
1.A.2.B.3.A.4.C.5.B.6.C.7.B.8.C.9.A.10.A.
二.填空题(共5小题)
11. 2 .12.(6+2)a .13. 150a元 .14. AB=AD 15. 等腰直角
三.解答题(共5小题)
16.证明:(1)在△ABC和△DCB中,∠A=∠D=90°,AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形
∵Rt△ABC≌Rt△DCB∴∠ACB=∠DCB∴OB=OC∴△OBC是等腰三角形
17.证明:∵AD∥BC,∴∠ADB=∠DBC.
∵CE⊥BD,∴∠BEC=90°.
∵∠A=90°,∴∠A=∠BEC.
∵BD=BC,∴△ABD≌△BCE.∴AD=BE.
18.解:延长DA,CB,交于点E,∵∠ABE=∠D=90°,∠C=60°∴∠E=30°,
在Rt△DCE中∵CD=3,∴CE=6;∵BC=4,所以BE=2。
设AB=x,则有AE=2x,根据勾股定理得:x2+22=(2x)2,
解得:x=,
(18题图) (20题图)
19.解:(1)∵AD平分∠CAB,∠C=90°,DE⊥AB,∴CD=DE=5,
∵∠B=30°,∴BD=2DE=10,
(2)AE与BE相等,理由如下:
∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°,
∵AD平分∠CAB交CB于点D,∴∠DAB=30°,∴AD=BD,
∵DE⊥AB,∴AE=BE.
20.证明:(1)∵△ABC和△DBE均为等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,即∠ABD=∠CBE,
∴△ABD≌△CBE,∴AD=CE.
(2)延长AD分别交BC和CE于G和F,
∵△ABD≌△CBE,
∴∠BAD=∠BCE,
∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°,
又∵∠BGA=∠CGF,
∴∠AFC=∠ABC=90°,
∴AD⊥CE.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
