3.1.5 圆柱的体积 课件-人教版数学六年级下册(共25张PPT)
文档属性
| 名称 | 3.1.5 圆柱的体积 课件-人教版数学六年级下册(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第3课时 圆柱的体积
第三单元 圆柱与圆锥
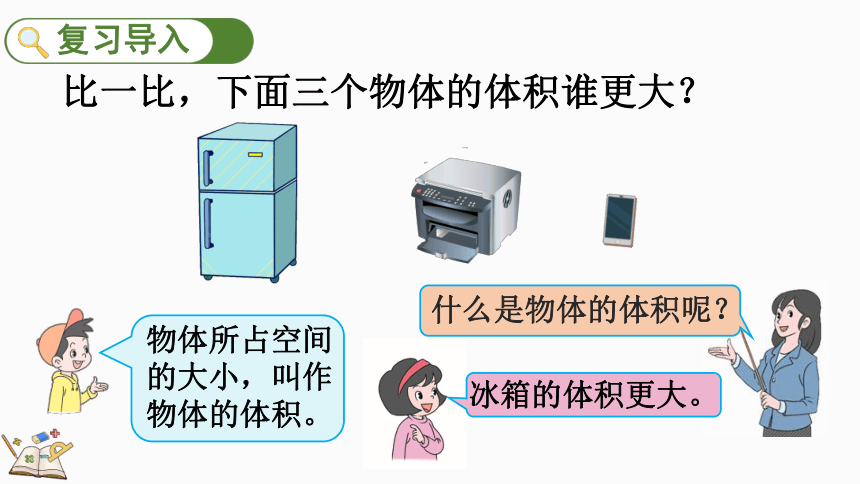
物体所占空间的大小,叫作物体的体积。
比一比,下面三个物体的体积谁更大?
什么是物体的体积呢?
冰箱的体积更大。
6
3
4
4
4
4
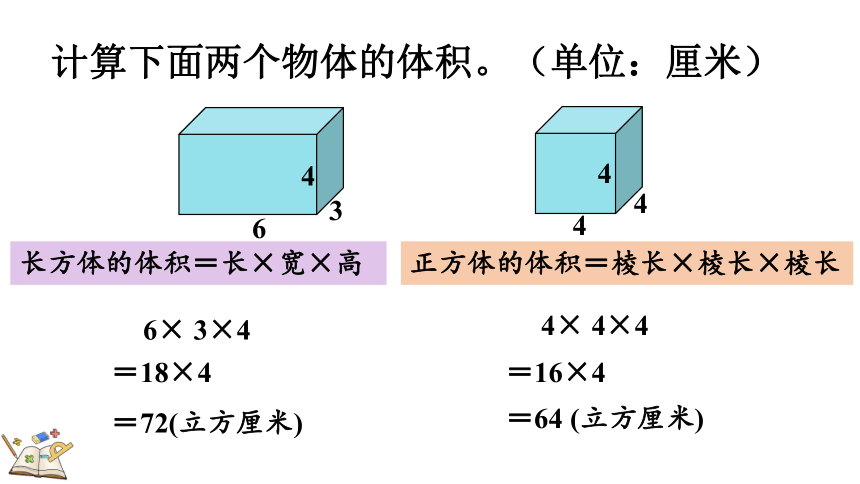
计算下面两个物体的体积。(单位:厘米)
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
6× 3×4
=18×4
=72(立方厘米)
4× 4×4
=64 (立方厘米)
=16×4
5
我们会计算长方体和正方体的体积,怎样计算圆柱的体积呢?能不能将圆柱转化成我们学过的立体图形,再计算出它的体积呢?
1.利用手中的学具拼一拼,摆一摆,独立思考如何将圆柱转换为长、正方体。
2.在小组内说一说如何计算圆柱的体积。
小组讨论
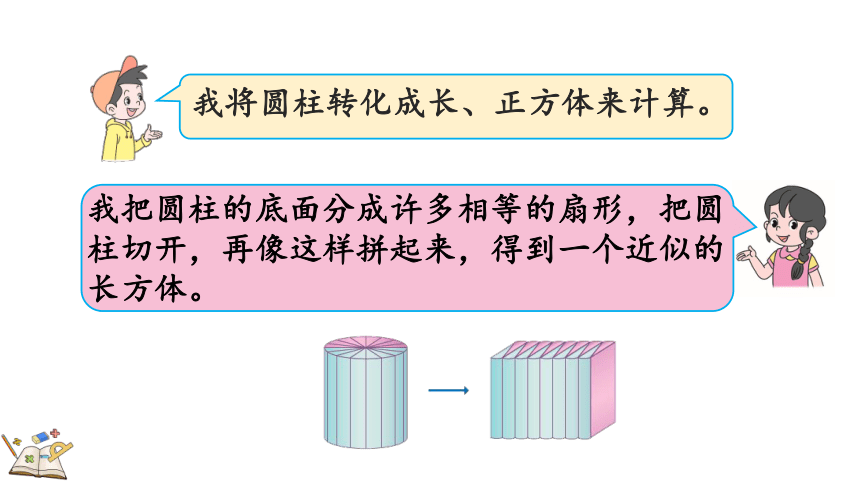
我将圆柱转化成长、正方体来计算。
我把圆柱的底面分成许多相等的扇形,把圆柱切开,再像这样拼起来,得到一个近似的长方体。
回顾一下圆的面积是如何推导出来的。
r
S= ·r = =πr
仔细观看你发现这种两种方法有何联系?
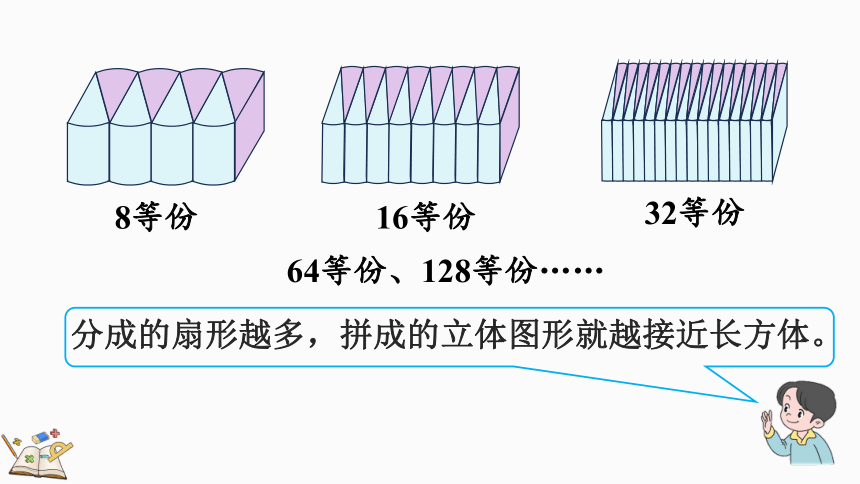
8等份
16等份
32等份
64等份、128等份……
分成的扇形越多,拼成的立体图形就越接近长方体。
把长方体与原来的圆柱比较,你能发现什么?
h
h
这个长方体的底面积等于圆柱的________,高等于圆柱的________。
底面积
高
=
高不变
=
如果用V表示圆柱的的体积,S表示底面积, h表示高,那么圆柱的体积公式是:
长方体的体积
底面积
高
圆柱的体积
底面积
高
= ×
V=Sh
= ×
选自教材第24页做一做第1题
1
一根圆柱形木料,底面积为75cm2 ,长90cm。它的体积是多少?
75 ×90 =6750(cm3)
答:它的体积是6750cm3。
V圆柱 =Sh
高
S
(1)如果熔成一个底面半径为1m,高是2m的圆柱。圆柱的体积是多少立方米?
根据教材第24页做一做第2题改编
答:圆柱的体积是6.28m3。
3.14× 12 ×2
=3.14×1×2
=6.28 (m3)
求V
r
h
=πr h
S=πr
V=Sh
环保厂有一批废旧钢铁准备熔化再利用。
2
S
(2)如果熔成一个底面直径为2m,高是2m的圆柱。圆柱的体积是多少立方米?
环保厂有一批废旧钢铁准备熔化再利用。
2
3.14× (2÷2)2 ×2
=3.14×1×2
=6.28 (m3)
求V
d
h
V=Sh=πr2h
r
答:圆柱的体积是6.28m3。
r=
=π ( )2h
根据教材第24页做一做第2题改编
V=πr2h
(3)如果熔成一个底面周长为6.28m,高是2m的圆柱。圆柱的体积是多少立方米?
环保厂有一批废旧钢铁准备熔化再利用。
2
3.14× (6.28÷2÷3.24)2 ×2
=3.14×1×2
=6.28 (m3)
求V
C
h
r
答:圆柱的体积是6.28m3。
r=C÷2π
=π(C÷2π)2h
根据教材第24页做一做第2题改编
(4)你有什么发现?
环保厂有一批废旧钢铁准备熔化再利用。
2
=πr2h
V=sh
= π ( )2h
=π(C÷2π)2h
根据教材第24页做一做第2题改编
选自教材第24页做一做第2题
挖一口圆柱形水井,地面以下的井深10m,底面直径为1m。挖出的土有多少立方米?
3
答:挖出的土有7.85m3。
3.14× (1÷2)2 ×10
=3.14×0.25×10
=7.85 (m3)
V=π ( )2h
求V
h
d
1.填一填。
(1)一个圆柱形石墩的横截面积是0.5,高是0.8m,它的体积是( )m3。
(2)一根圆柱形水管的底面半径是2cm,高是5cm,将水管注满水,水的体积是( )cm3。
(3)一个圆柱的高不变,底面半径扩大到原来的3倍,它的体积( ) 。
0.4
62.8
扩大到原来的9倍
2.判断。
(1)圆柱的体积比表面积大。( )
(2)底面积相等的两个圆柱,它们的体积一定相等。( )
(3)等底等高的正方体、长方体和圆柱的体积都相等。( )
(4)一个圆柱的底面半径扩大到原来的3倍,高缩小到原来的,体积不变。( )
×
×
√
×
1.张老师用纸板做了一个学具,你能计算出它的体积吗?
16cm
14cm
10cm
16cm
(14+16)cm
10cm
14cm
3.14×(10÷2)×(14+16)÷2
=3.14×25×30÷2
=1177.5(cm3)
答:它的体积是1177.5cm3。
2.把一个半径为3cm,高为8cm的圆柱切拼成近似长方体后,表面积是否改变?怎么变的?
3×8 × 2=48(cm )
答:表面积增加,增加了48cm 。
S长方体的表面积=S长方体前后面+S长方体上下面+S长方体左右面
S圆柱表面积=S圆柱侧面+S圆柱的底面
S圆柱侧面
S圆柱的底面
S长方体前后面
S长方体上下面
S长方体左右面
这节课有什么收获呢?
圆柱的体积=底面积×高
=πr2h
V=sh
= π ( )2h
=π(C÷2π)2h
1.教材第27页练习五第1、4题;
2.从课时练中选取。
在建筑领域,立柱做成空心的,多见于钢结构的格构柱。
建筑中的立柱为什么是空心的而不是实心的?
当然空心结构还能够节省一部分钢材,节约成本。
其目的一是为了减轻质量;
二是加强抗弯和抗压强度;
三是消震作用;
四是阻音隔热。
圆柱的体积
V=sh
=πr2h
长方体的体积
底面积
高
圆柱的体积
底面积
高
= ×
= ×
=π ( )2h
=π(C÷2π)2h
第3课时 圆柱的体积
第三单元 圆柱与圆锥
物体所占空间的大小,叫作物体的体积。
比一比,下面三个物体的体积谁更大?
什么是物体的体积呢?
冰箱的体积更大。
6
3
4
4
4
4
计算下面两个物体的体积。(单位:厘米)
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
6× 3×4
=18×4
=72(立方厘米)
4× 4×4
=64 (立方厘米)
=16×4
5
我们会计算长方体和正方体的体积,怎样计算圆柱的体积呢?能不能将圆柱转化成我们学过的立体图形,再计算出它的体积呢?
1.利用手中的学具拼一拼,摆一摆,独立思考如何将圆柱转换为长、正方体。
2.在小组内说一说如何计算圆柱的体积。
小组讨论
我将圆柱转化成长、正方体来计算。
我把圆柱的底面分成许多相等的扇形,把圆柱切开,再像这样拼起来,得到一个近似的长方体。
回顾一下圆的面积是如何推导出来的。
r
S= ·r = =πr
仔细观看你发现这种两种方法有何联系?
8等份
16等份
32等份
64等份、128等份……
分成的扇形越多,拼成的立体图形就越接近长方体。
把长方体与原来的圆柱比较,你能发现什么?
h
h
这个长方体的底面积等于圆柱的________,高等于圆柱的________。
底面积
高
=
高不变
=
如果用V表示圆柱的的体积,S表示底面积, h表示高,那么圆柱的体积公式是:
长方体的体积
底面积
高
圆柱的体积
底面积
高
= ×
V=Sh
= ×
选自教材第24页做一做第1题
1
一根圆柱形木料,底面积为75cm2 ,长90cm。它的体积是多少?
75 ×90 =6750(cm3)
答:它的体积是6750cm3。
V圆柱 =Sh
高
S
(1)如果熔成一个底面半径为1m,高是2m的圆柱。圆柱的体积是多少立方米?
根据教材第24页做一做第2题改编
答:圆柱的体积是6.28m3。
3.14× 12 ×2
=3.14×1×2
=6.28 (m3)
求V
r
h
=πr h
S=πr
V=Sh
环保厂有一批废旧钢铁准备熔化再利用。
2
S
(2)如果熔成一个底面直径为2m,高是2m的圆柱。圆柱的体积是多少立方米?
环保厂有一批废旧钢铁准备熔化再利用。
2
3.14× (2÷2)2 ×2
=3.14×1×2
=6.28 (m3)
求V
d
h
V=Sh=πr2h
r
答:圆柱的体积是6.28m3。
r=
=π ( )2h
根据教材第24页做一做第2题改编
V=πr2h
(3)如果熔成一个底面周长为6.28m,高是2m的圆柱。圆柱的体积是多少立方米?
环保厂有一批废旧钢铁准备熔化再利用。
2
3.14× (6.28÷2÷3.24)2 ×2
=3.14×1×2
=6.28 (m3)
求V
C
h
r
答:圆柱的体积是6.28m3。
r=C÷2π
=π(C÷2π)2h
根据教材第24页做一做第2题改编
(4)你有什么发现?
环保厂有一批废旧钢铁准备熔化再利用。
2
=πr2h
V=sh
= π ( )2h
=π(C÷2π)2h
根据教材第24页做一做第2题改编
选自教材第24页做一做第2题
挖一口圆柱形水井,地面以下的井深10m,底面直径为1m。挖出的土有多少立方米?
3
答:挖出的土有7.85m3。
3.14× (1÷2)2 ×10
=3.14×0.25×10
=7.85 (m3)
V=π ( )2h
求V
h
d
1.填一填。
(1)一个圆柱形石墩的横截面积是0.5,高是0.8m,它的体积是( )m3。
(2)一根圆柱形水管的底面半径是2cm,高是5cm,将水管注满水,水的体积是( )cm3。
(3)一个圆柱的高不变,底面半径扩大到原来的3倍,它的体积( ) 。
0.4
62.8
扩大到原来的9倍
2.判断。
(1)圆柱的体积比表面积大。( )
(2)底面积相等的两个圆柱,它们的体积一定相等。( )
(3)等底等高的正方体、长方体和圆柱的体积都相等。( )
(4)一个圆柱的底面半径扩大到原来的3倍,高缩小到原来的,体积不变。( )
×
×
√
×
1.张老师用纸板做了一个学具,你能计算出它的体积吗?
16cm
14cm
10cm
16cm
(14+16)cm
10cm
14cm
3.14×(10÷2)×(14+16)÷2
=3.14×25×30÷2
=1177.5(cm3)
答:它的体积是1177.5cm3。
2.把一个半径为3cm,高为8cm的圆柱切拼成近似长方体后,表面积是否改变?怎么变的?
3×8 × 2=48(cm )
答:表面积增加,增加了48cm 。
S长方体的表面积=S长方体前后面+S长方体上下面+S长方体左右面
S圆柱表面积=S圆柱侧面+S圆柱的底面
S圆柱侧面
S圆柱的底面
S长方体前后面
S长方体上下面
S长方体左右面
这节课有什么收获呢?
圆柱的体积=底面积×高
=πr2h
V=sh
= π ( )2h
=π(C÷2π)2h
1.教材第27页练习五第1、4题;
2.从课时练中选取。
在建筑领域,立柱做成空心的,多见于钢结构的格构柱。
建筑中的立柱为什么是空心的而不是实心的?
当然空心结构还能够节省一部分钢材,节约成本。
其目的一是为了减轻质量;
二是加强抗弯和抗压强度;
三是消震作用;
四是阻音隔热。
圆柱的体积
V=sh
=πr2h
长方体的体积
底面积
高
圆柱的体积
底面积
高
= ×
= ×
=π ( )2h
=π(C÷2π)2h
