苏科版2023-2024学年七年级下册数学7.1探索直线平行的条件同步练习(附答案)
文档属性
| 名称 | 苏科版2023-2024学年七年级下册数学7.1探索直线平行的条件同步练习(附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 659.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 20:32:28 | ||
图片预览


文档简介
苏科版2023-2024学年七年级下册数学7.1探索直线平行的条件
同步练习
姓名:___________班级:___________考号:___________
一、单选题
1.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( ).
A.∠1 B.∠2 C.∠4 D.∠5
2.下列说法正确的是( )
A.一条直线的平行线有且只有一条
B.经过一点有且只有一条直线与已知直线平行
C.经过一点有两条直线与已知直线平行
D.过直线外一点有且只有一条直线与已知直线平行
3.下列说法中,正确的是( )
A.在同一平面内,过一点有且只有一条直线与已知直线平行
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.从直线外一点作这条直线的垂线段叫做点到这条直线的距离
D.不相交的两条线段是平行线
4.如图,下列说法不正确的是( )
A.与是内错角 B.与是内错角
C.与是同旁内角 D.与是同位角
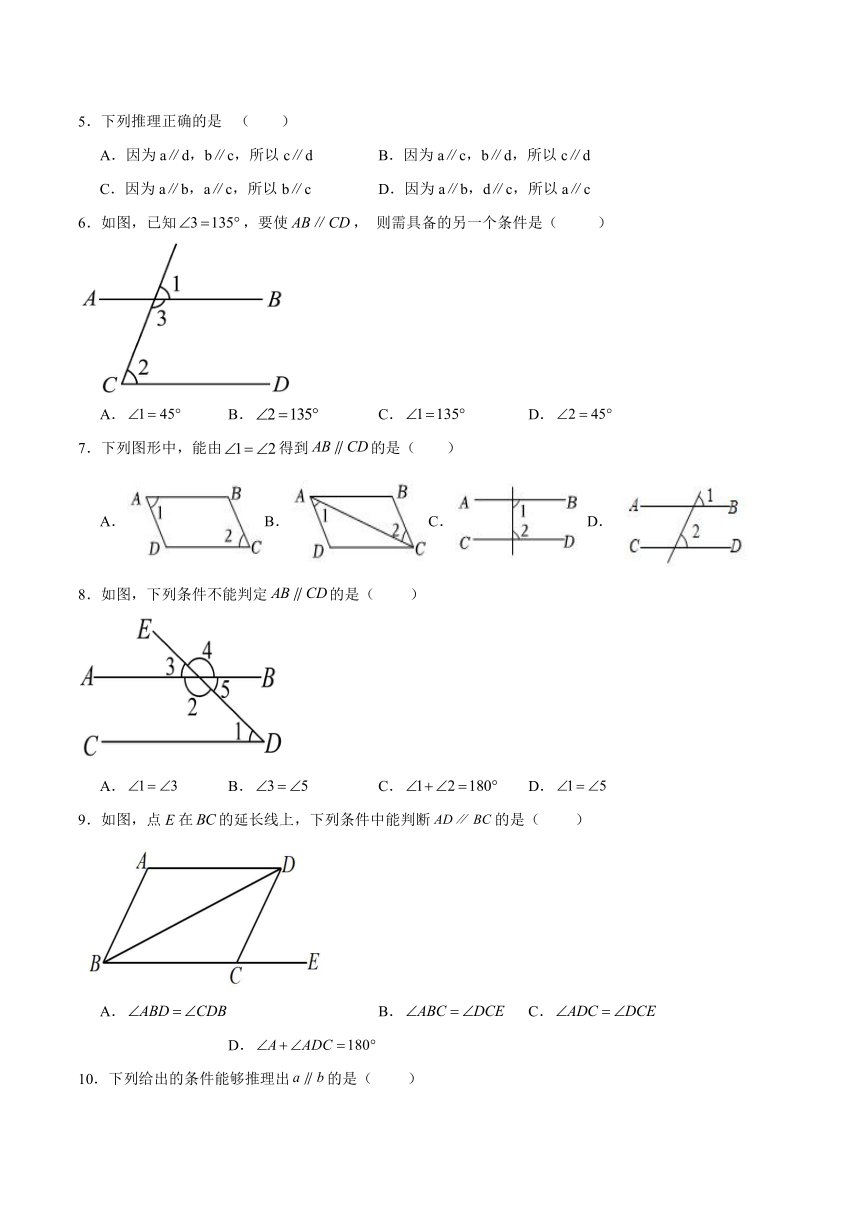
5.下列推理正确的是 ( )
A.因为a∥d,b∥c,所以c∥d B.因为a∥c,b∥d,所以c∥d
C.因为a∥b,a∥c,所以b∥c D.因为a∥b,d∥c,所以a∥c
6.如图,已知,要使, 则需具备的另一个条件是( )
A. B. C. D.
7.下列图形中,能由得到的是( )
A.B.C. D.
8.如图,下列条件不能判定的是( )
A. B. C. D.
9.如图,点E在的延长线上,下列条件中能判断的是( )
A. B. C. D.
10.下列给出的条件能够推理出的是( )
A. B. C. D.
11.若,,则与的关系是( )
A.平行 B.垂直 C.相交 D.以上都不对
12.如图所示,和是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
二、填空题
13.如图:①和是 角;②和是 角.
14.平行的基本事实:经过直线外一点,有且只有 直线与这条直线平行.
15.定理:平行于同一条直线的两条直线 .
16.如图,∠A=70°,O是AB上一点,直线CO与AB所夹的∠BOC=82°.当直线OC绕点O按逆时针方向旋转 时,OC//AD.
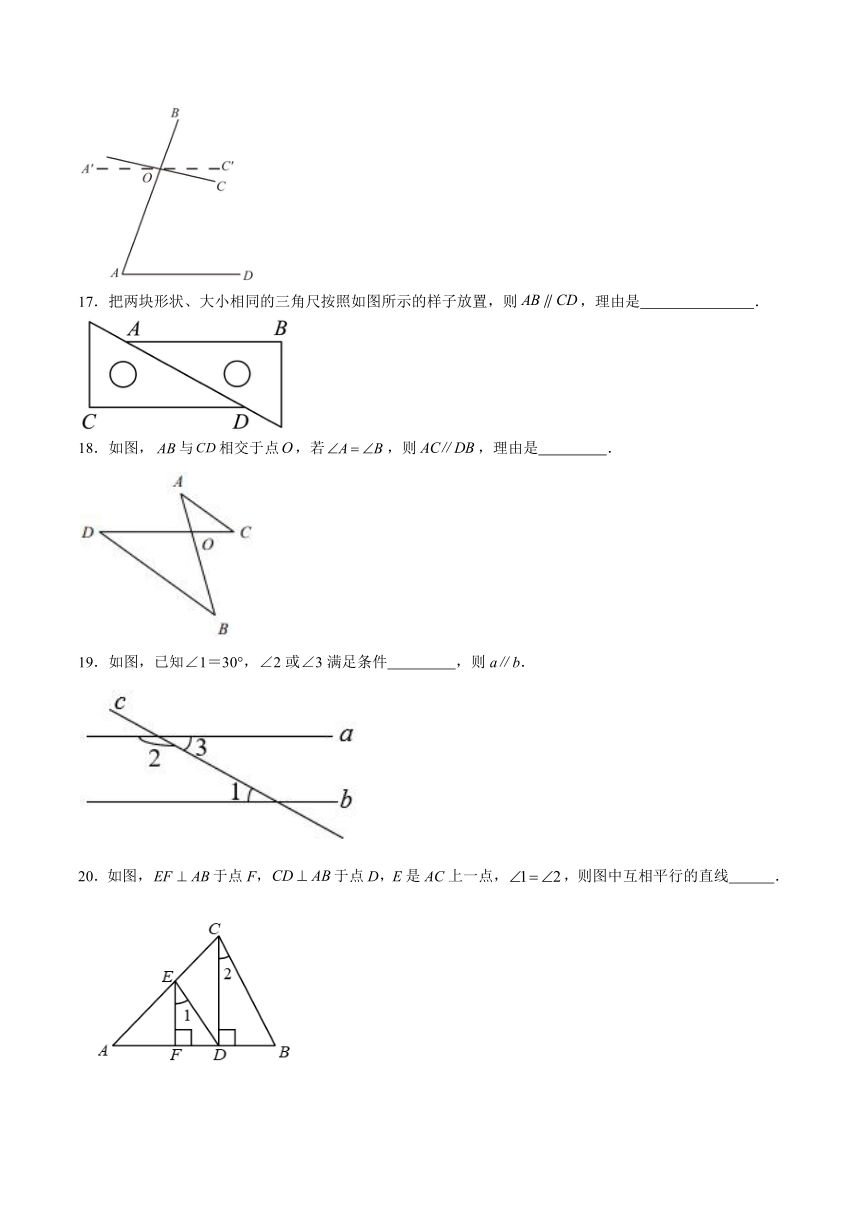
17.把两块形状、大小相同的三角尺按照如图所示的样子放置,则,理由是 .
18.如图,与相交于点,若,则,理由是 .
19.如图,已知∠1=30°,∠2或∠3满足条件 ,则a∥b.
20.如图,于点F,于点D,E是AC上一点,,则图中互相平行的直线 .
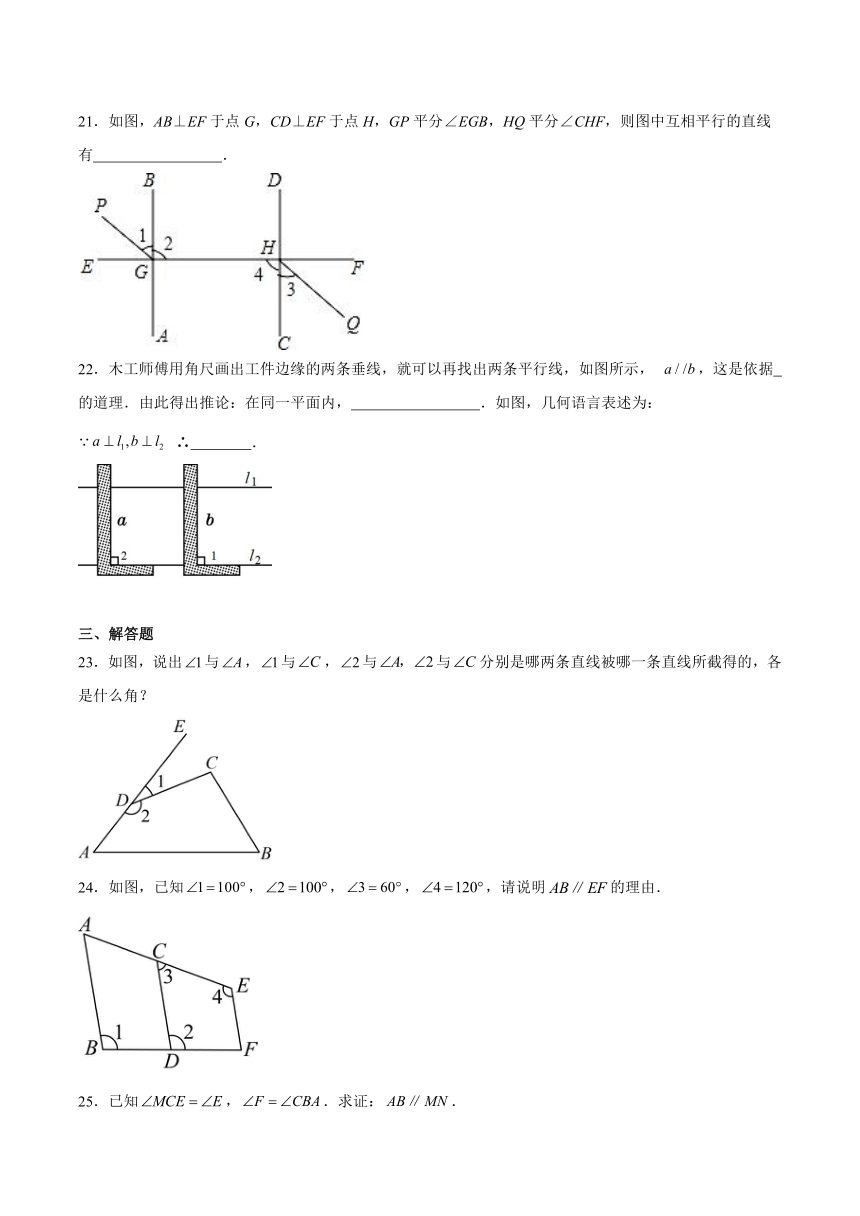
21.如图,AB⊥EF于点G,CD⊥EF于点H,GP平分∠EGB,HQ平分∠CHF,则图中互相平行的直线有 .
22.木工师傅用角尺画出工件边缘的两条垂线,就可以再找出两条平行线,如图所示, ,这是依据 的道理.由此得出推论:在同一平面内, .如图,几何语言表述为: ∴ .
三、解答题
23.如图,说出与,与,与与分别是哪两条直线被哪一条直线所截得的,各是什么角?
24.如图,已知,,,,请说明的理由.
25.已知,.求证:.
26.如图,已知于点E,于点G,,能成立吗?为什么?
27.如图所示,一块玻璃不小心被打碎了,只有一条边是直的,为了废物利用,工人师傅要把它裁成一块长方形,先用一把直尺作,,这样裁剪以后,和是否平行?并说明理由.
28.光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知,.请你用所学知识来判断c与d是否平行?并说明理由.
29.如图,直线、被所截,于H,,,求证:.
30.如图,如果,求证:;.
观察下面的解答过程,补充必要的依据或结论.
证明:∵(已知),
(______________),
∴(_______________),
又∵(已知),
∴(____________)(等式的性质)
∴(_______________)
又∵(_____________),
∴(等式的性质)
∵(已知),
∴,
∴(___________________________)
31.在四边形ABCD中,CF⊥BD于点F,过点A作AG⊥BD,分别交BD,BC于点E,G,若∠DAG=∠BCF,求证:AD∥BC.
32.如图,已知点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D,F,点M,G在AB上,GF交BD于点H,∠BMD+∠ABC=180°,∠1=∠2,求证:MDGF.
下面是小颖同学的思考过程,请补全证明过程并在括号内填上证明依据.
证明:∵BD⊥AC,EF⊥AC,
∴∠BDC=90°,∠EFC=90°(① ).
∴∠BDC=∠EFC(等量代换).
∴BDEF(同位角相等,两直线平行).
∴∠2=∠CBD( ② ).
∵∠1=∠2(已知).
∴∠1=∠CBD(等量代换).
∴③ (内错角相等,两直线平行).
∵∠BMD+∠ABC=180°(已知),
∴MDBC(④ ).
∴MDGF(⑤ ).
答案:
1.根据同旁内角的定义可得∠3的内错角是∠2.
故答案选:B
2.A. 一条直线的平行线有无数条,故本选项错误;
B. 过直线外一点有且只有一条直线与已知直线平行,故本选项错误;
C. 过直线外一点有且只有一条直线与已知直线平行,故本选项错误;
D. 过直线外一点有且只有一条直线与已知直线平行,故本选项正确.
故选D.
3.A. 过直线外一点,有且只有一条直线与已知直线平行,故此选项错误;
B. 在同一平面内,过一点有且只有一条直线与已知直线垂直,故此选项正确;
C. 从直线外一点到这条直线的垂线段长,叫做这点到这条直线的距离,故此选项错误;
D. 在同一平面内,不相交的两条直线是平行线,故此选项错误.
故选B.
4.解:A. 与是内错角,故该选项正确,不符合题意;
B. 与是同旁内角,故该选项不正确,符合题意;
C. 与是同旁内角,故该选项正确,不符合题意;
D. 与是同位角,故该选项正确,不符合题意;
故选:B.
5.解:A、由a∥d,b∥c,不能推出c∥d,所以本选项推理错误,不符合题意;
B、由a∥c,b∥d,不能推出c∥d,所以本选项推理错误,不符合题意;
C、由a∥b,a∥c,能推出b∥c,所以本选项推理正确,符合题意;
D、由a∥b,d∥c,不能推出a∥c,所以本选项推理错误,不符合题意.
故选:C.
6.解:∵
∴
当时,,,可得
故选:D
7.解:A选项中由不能得到,
不符合题意;
B选项中由得到,
不符合题意;
C选项中由不能得到,
不符合题意;
D选项中由得到,
符合题意;
故选:D.
【点睛】本题考查了平行线的判定定理,熟练掌握平行线的判定定理是解题的关键.
8.解:A、,根据同位角相等,两直线平行可判定,故此选项不符合题意;
B、,对顶角相等,不能判定,故此选项符合题意;
C、,根据同旁内角互补,两直线平行可判定,此选项不符合题意;
D、,根据内错角相等,两直线平行可判定,故此选项不符合题意;
故选:B.
9.解:由,可以根据内错角相等,两直线平行判断,不能判断,故A不符合题意;
由,可以根据同位角相等,两直线平行判断,不能判断,故B不符合题意;
由,可以根据内错角相等,两直线平行判断,故C不符合题意;
由,可以根据同旁内角互补相等,两直线平行判断,不能判断,故D不符合题意;
故选C.
10.解:A.由不能推理出,故不符合题意;
B.由不能推理出,故不符合题意;
C.由不能推理出,故不符合题意;
D. ∵∠4+∠5=180°时能推出,又∵∠1=∠5,∴由能推理出,故符合题意;
故选D.
11.解:当直线a、b、c在同一平面内时,,,则.
当直线a、b、c不在同一平面内时,,,与的关系不一定平行.
故选:D.
12.解:由图可知,和是同旁内角,故C正确.
故选:C.
13.解:和是和被所截形成的内错角;
和是和被所截形成的同位角;
故答案为:内错,同位
14.我们学过的基本事实有,过直线外一点有且只有一条直线与已知直线平行.
故答案为
一条.
15.平行
16.解:∵∠BOC与∠A为同位角,
∴当∠BOC'=∠A=70°时,OC∥AD,
∵∠BOC=82°,
则直线OC绕点O按逆时针方向旋转82°-70°=12°.
故答案为12°.
17.解:由题意可得:,
(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
18.解:∵∠A=∠B,
∴AC∥DB(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
19.∠2=150°或∠3=30°
20.,
21.解:∵EF⊥AB,CD⊥EF,
∴AB∥CD,∠EGB=∠CHF=90°,
∴∠2=∠4,
又∵GP平分∠EGB,HQ平分∠CHF,
∴∠1=∠3,∴∠PGH=∠GHQ,
∴PG∥HQ,
∴图中互相平行的直线是AB∥CD,PG∥HQ.
故答案为:AB∥CD,PG∥HQ.
22.,
,(同位角相等,两直线平行)
由此得出推论:
在同一平面内,垂直于同一直线的两条直线互相平行,
几何语言表述为:
,
∴,
故答案为:同位角相等,两直线平行;垂直于同一直线的两条直线互相平行;.
23.解:与是直线和直线被直线所截得的同位角;
与是直线和直线被直线所截得的内错角;
与是直线和直线被直线所截得的同旁内角;
与是直线和直线被直线所截得的同旁内角
24.解:因为,,
所以,
所以(同位角相等,两直线平行).
因为,,
所以,
所以(同旁内角互补,两直线平行).
所以(平行于同一条直线的两条直线平行).
25.证明:∵,
∴
∵,
∴,
∴.
26.证明:∵,,
∴,
∴,
∵,
∴,
∴.
27.解:和平行,理由如下:
∵,
∴
∴
28.解:,理由如下:
∵,,
∴,
∵,
∴,
∴.
29.证明:∵,
∴
∴
∴
∵
∴
∴.
30.证明:∵(已知),
(对顶角相等),
∴(等量代换),
又∵(已知),
∴()(等式的性质)
∴(同旁内角互补,两直线平行)
又∵(邻补角互补),
∴(等式的性质)
∵(已知),
∴,
∴(内错角相等,两直线平行)
故答案为:对顶角相等;等量代换;;同旁内角互补,两直线平行;邻补角互补;内错角相等,两直线平行.
31.证明:∵CF⊥BD,AG⊥BD,
∴CF∥AG,
∴∠BGA=∠BCF,
∵∠DAG=∠BCF,
∴∠BGA=∠DAG,
∴AD∥BC.
32.证明:∵BD⊥AC,EF⊥AC,
∴∠BDC=90°,∠EFC=90°(垂直的定义).
∴∠BDC=∠EFC(等量代换).
∴BD∥EF(同位角相等,两直线平行).
∴∠2=∠CBD(两直线平行,同位角相等).
∵∠1=∠2(已知).
∴∠1=∠CBD(等量代换).
∴GF∥BC(内错角相等,两直线平行).
∵∠BMD+∠ABC=180°(已知),
∴MD∥BC(同旁内角互补,两直线平行).
∴MD∥GF(平行于同一直线的两直线平行).
故答案为:垂直的定义;两直线平行,同位角相等;GF∥BC;同旁内角互补,两直线平行;平行于同一直线的两直线平行.
同步练习
姓名:___________班级:___________考号:___________
一、单选题
1.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( ).
A.∠1 B.∠2 C.∠4 D.∠5
2.下列说法正确的是( )
A.一条直线的平行线有且只有一条
B.经过一点有且只有一条直线与已知直线平行
C.经过一点有两条直线与已知直线平行
D.过直线外一点有且只有一条直线与已知直线平行
3.下列说法中,正确的是( )
A.在同一平面内,过一点有且只有一条直线与已知直线平行
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.从直线外一点作这条直线的垂线段叫做点到这条直线的距离
D.不相交的两条线段是平行线
4.如图,下列说法不正确的是( )
A.与是内错角 B.与是内错角
C.与是同旁内角 D.与是同位角
5.下列推理正确的是 ( )
A.因为a∥d,b∥c,所以c∥d B.因为a∥c,b∥d,所以c∥d
C.因为a∥b,a∥c,所以b∥c D.因为a∥b,d∥c,所以a∥c
6.如图,已知,要使, 则需具备的另一个条件是( )
A. B. C. D.
7.下列图形中,能由得到的是( )
A.B.C. D.
8.如图,下列条件不能判定的是( )
A. B. C. D.
9.如图,点E在的延长线上,下列条件中能判断的是( )
A. B. C. D.
10.下列给出的条件能够推理出的是( )
A. B. C. D.
11.若,,则与的关系是( )
A.平行 B.垂直 C.相交 D.以上都不对
12.如图所示,和是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
二、填空题
13.如图:①和是 角;②和是 角.
14.平行的基本事实:经过直线外一点,有且只有 直线与这条直线平行.
15.定理:平行于同一条直线的两条直线 .
16.如图,∠A=70°,O是AB上一点,直线CO与AB所夹的∠BOC=82°.当直线OC绕点O按逆时针方向旋转 时,OC//AD.
17.把两块形状、大小相同的三角尺按照如图所示的样子放置,则,理由是 .
18.如图,与相交于点,若,则,理由是 .
19.如图,已知∠1=30°,∠2或∠3满足条件 ,则a∥b.
20.如图,于点F,于点D,E是AC上一点,,则图中互相平行的直线 .
21.如图,AB⊥EF于点G,CD⊥EF于点H,GP平分∠EGB,HQ平分∠CHF,则图中互相平行的直线有 .
22.木工师傅用角尺画出工件边缘的两条垂线,就可以再找出两条平行线,如图所示, ,这是依据 的道理.由此得出推论:在同一平面内, .如图,几何语言表述为: ∴ .
三、解答题
23.如图,说出与,与,与与分别是哪两条直线被哪一条直线所截得的,各是什么角?
24.如图,已知,,,,请说明的理由.
25.已知,.求证:.
26.如图,已知于点E,于点G,,能成立吗?为什么?
27.如图所示,一块玻璃不小心被打碎了,只有一条边是直的,为了废物利用,工人师傅要把它裁成一块长方形,先用一把直尺作,,这样裁剪以后,和是否平行?并说明理由.
28.光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知,.请你用所学知识来判断c与d是否平行?并说明理由.
29.如图,直线、被所截,于H,,,求证:.
30.如图,如果,求证:;.
观察下面的解答过程,补充必要的依据或结论.
证明:∵(已知),
(______________),
∴(_______________),
又∵(已知),
∴(____________)(等式的性质)
∴(_______________)
又∵(_____________),
∴(等式的性质)
∵(已知),
∴,
∴(___________________________)
31.在四边形ABCD中,CF⊥BD于点F,过点A作AG⊥BD,分别交BD,BC于点E,G,若∠DAG=∠BCF,求证:AD∥BC.
32.如图,已知点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D,F,点M,G在AB上,GF交BD于点H,∠BMD+∠ABC=180°,∠1=∠2,求证:MDGF.
下面是小颖同学的思考过程,请补全证明过程并在括号内填上证明依据.
证明:∵BD⊥AC,EF⊥AC,
∴∠BDC=90°,∠EFC=90°(① ).
∴∠BDC=∠EFC(等量代换).
∴BDEF(同位角相等,两直线平行).
∴∠2=∠CBD( ② ).
∵∠1=∠2(已知).
∴∠1=∠CBD(等量代换).
∴③ (内错角相等,两直线平行).
∵∠BMD+∠ABC=180°(已知),
∴MDBC(④ ).
∴MDGF(⑤ ).
答案:
1.根据同旁内角的定义可得∠3的内错角是∠2.
故答案选:B
2.A. 一条直线的平行线有无数条,故本选项错误;
B. 过直线外一点有且只有一条直线与已知直线平行,故本选项错误;
C. 过直线外一点有且只有一条直线与已知直线平行,故本选项错误;
D. 过直线外一点有且只有一条直线与已知直线平行,故本选项正确.
故选D.
3.A. 过直线外一点,有且只有一条直线与已知直线平行,故此选项错误;
B. 在同一平面内,过一点有且只有一条直线与已知直线垂直,故此选项正确;
C. 从直线外一点到这条直线的垂线段长,叫做这点到这条直线的距离,故此选项错误;
D. 在同一平面内,不相交的两条直线是平行线,故此选项错误.
故选B.
4.解:A. 与是内错角,故该选项正确,不符合题意;
B. 与是同旁内角,故该选项不正确,符合题意;
C. 与是同旁内角,故该选项正确,不符合题意;
D. 与是同位角,故该选项正确,不符合题意;
故选:B.
5.解:A、由a∥d,b∥c,不能推出c∥d,所以本选项推理错误,不符合题意;
B、由a∥c,b∥d,不能推出c∥d,所以本选项推理错误,不符合题意;
C、由a∥b,a∥c,能推出b∥c,所以本选项推理正确,符合题意;
D、由a∥b,d∥c,不能推出a∥c,所以本选项推理错误,不符合题意.
故选:C.
6.解:∵
∴
当时,,,可得
故选:D
7.解:A选项中由不能得到,
不符合题意;
B选项中由得到,
不符合题意;
C选项中由不能得到,
不符合题意;
D选项中由得到,
符合题意;
故选:D.
【点睛】本题考查了平行线的判定定理,熟练掌握平行线的判定定理是解题的关键.
8.解:A、,根据同位角相等,两直线平行可判定,故此选项不符合题意;
B、,对顶角相等,不能判定,故此选项符合题意;
C、,根据同旁内角互补,两直线平行可判定,此选项不符合题意;
D、,根据内错角相等,两直线平行可判定,故此选项不符合题意;
故选:B.
9.解:由,可以根据内错角相等,两直线平行判断,不能判断,故A不符合题意;
由,可以根据同位角相等,两直线平行判断,不能判断,故B不符合题意;
由,可以根据内错角相等,两直线平行判断,故C不符合题意;
由,可以根据同旁内角互补相等,两直线平行判断,不能判断,故D不符合题意;
故选C.
10.解:A.由不能推理出,故不符合题意;
B.由不能推理出,故不符合题意;
C.由不能推理出,故不符合题意;
D. ∵∠4+∠5=180°时能推出,又∵∠1=∠5,∴由能推理出,故符合题意;
故选D.
11.解:当直线a、b、c在同一平面内时,,,则.
当直线a、b、c不在同一平面内时,,,与的关系不一定平行.
故选:D.
12.解:由图可知,和是同旁内角,故C正确.
故选:C.
13.解:和是和被所截形成的内错角;
和是和被所截形成的同位角;
故答案为:内错,同位
14.我们学过的基本事实有,过直线外一点有且只有一条直线与已知直线平行.
故答案为
一条.
15.平行
16.解:∵∠BOC与∠A为同位角,
∴当∠BOC'=∠A=70°时,OC∥AD,
∵∠BOC=82°,
则直线OC绕点O按逆时针方向旋转82°-70°=12°.
故答案为12°.
17.解:由题意可得:,
(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
18.解:∵∠A=∠B,
∴AC∥DB(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
19.∠2=150°或∠3=30°
20.,
21.解:∵EF⊥AB,CD⊥EF,
∴AB∥CD,∠EGB=∠CHF=90°,
∴∠2=∠4,
又∵GP平分∠EGB,HQ平分∠CHF,
∴∠1=∠3,∴∠PGH=∠GHQ,
∴PG∥HQ,
∴图中互相平行的直线是AB∥CD,PG∥HQ.
故答案为:AB∥CD,PG∥HQ.
22.,
,(同位角相等,两直线平行)
由此得出推论:
在同一平面内,垂直于同一直线的两条直线互相平行,
几何语言表述为:
,
∴,
故答案为:同位角相等,两直线平行;垂直于同一直线的两条直线互相平行;.
23.解:与是直线和直线被直线所截得的同位角;
与是直线和直线被直线所截得的内错角;
与是直线和直线被直线所截得的同旁内角;
与是直线和直线被直线所截得的同旁内角
24.解:因为,,
所以,
所以(同位角相等,两直线平行).
因为,,
所以,
所以(同旁内角互补,两直线平行).
所以(平行于同一条直线的两条直线平行).
25.证明:∵,
∴
∵,
∴,
∴.
26.证明:∵,,
∴,
∴,
∵,
∴,
∴.
27.解:和平行,理由如下:
∵,
∴
∴
28.解:,理由如下:
∵,,
∴,
∵,
∴,
∴.
29.证明:∵,
∴
∴
∴
∵
∴
∴.
30.证明:∵(已知),
(对顶角相等),
∴(等量代换),
又∵(已知),
∴()(等式的性质)
∴(同旁内角互补,两直线平行)
又∵(邻补角互补),
∴(等式的性质)
∵(已知),
∴,
∴(内错角相等,两直线平行)
故答案为:对顶角相等;等量代换;;同旁内角互补,两直线平行;邻补角互补;内错角相等,两直线平行.
31.证明:∵CF⊥BD,AG⊥BD,
∴CF∥AG,
∴∠BGA=∠BCF,
∵∠DAG=∠BCF,
∴∠BGA=∠DAG,
∴AD∥BC.
32.证明:∵BD⊥AC,EF⊥AC,
∴∠BDC=90°,∠EFC=90°(垂直的定义).
∴∠BDC=∠EFC(等量代换).
∴BD∥EF(同位角相等,两直线平行).
∴∠2=∠CBD(两直线平行,同位角相等).
∵∠1=∠2(已知).
∴∠1=∠CBD(等量代换).
∴GF∥BC(内错角相等,两直线平行).
∵∠BMD+∠ABC=180°(已知),
∴MD∥BC(同旁内角互补,两直线平行).
∴MD∥GF(平行于同一直线的两直线平行).
故答案为:垂直的定义;两直线平行,同位角相等;GF∥BC;同旁内角互补,两直线平行;平行于同一直线的两直线平行.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
