苏科版2023-2024学年七年级下册数学7.1探索直线平行的条件同步练习(含答案解析)
文档属性
| 名称 | 苏科版2023-2024学年七年级下册数学7.1探索直线平行的条件同步练习(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 990.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 00:00:00 | ||
图片预览



文档简介
苏科版2023-2024学年七年级下册数学7.1探索直线平行的条件
同步练习(含答案)
姓名:___________班级:___________考号:___________
一、单选题
1.对于下列四个说法:①两点之间,线段最短;②若,则C是线段的中点;③对顶角相等;④过一点有且只有一条直线与这条直线平行,其中,正确的有( )
A.0个 B.1个 C.2个 D.3个
2.下列说法中不正确的个数为( ).
①在同一平面内,两条直线的位置关系只有两种:相交和垂直.
②有且只有一条直线垂直于已知直线.
③如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
④从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.
⑤过一点,有且只有一条直线与已知直线平行.
A.2个 B.3个 C.4个 D.5个
3.如图,在下列给出的条件中,不能判定的是( )
A. B.
C. D.
4.如图,、分别在和内部,若,则下列条件中,不能判定的是( )
A. B.且
C.且 D.
(3题) (4题)
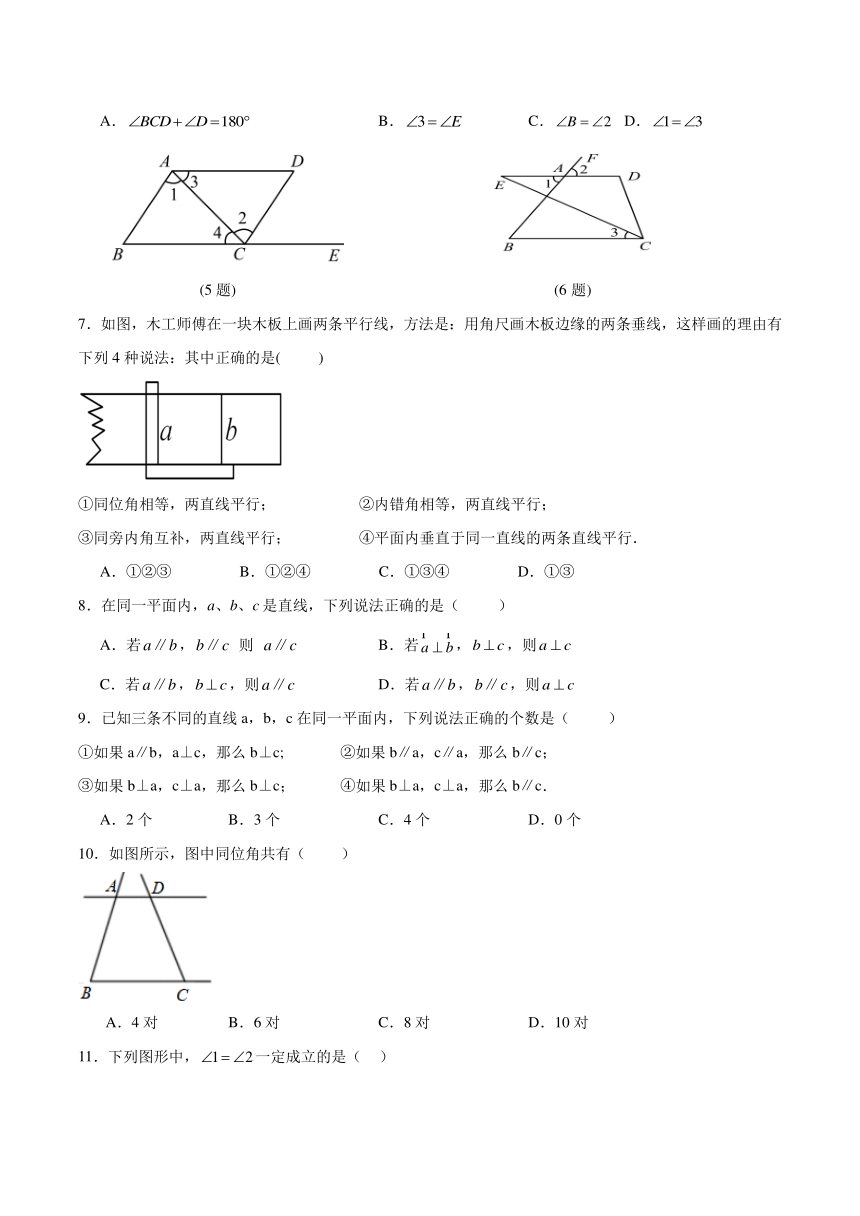
5.如图,点E在的延长线上,则下列条件中不能判定的是( )
A. B.
C. D.
6.如图,下列条件中,不能判断直线的是( )
A. B. C. D.
(5题) (6题)
7.如图,木工师傅在一块木板上画两条平行线,方法是:用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:其中正确的是( )
①同位角相等,两直线平行; ②内错角相等,两直线平行;
③同旁内角互补,两直线平行; ④平面内垂直于同一直线的两条直线平行.
A.①②③ B.①②④ C.①③④ D.①③
8.在同一平面内,a、b、c是直线,下列说法正确的是( )
A.若, 则 B.若,,则
C.若,,则 D.若,,则
9.已知三条不同的直线a,b,c在同一平面内,下列说法正确的个数是( )
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
A.2个 B.3个 C.4个 D.0个
10.如图所示,图中同位角共有( )
A.4对 B.6对 C.8对 D.10对
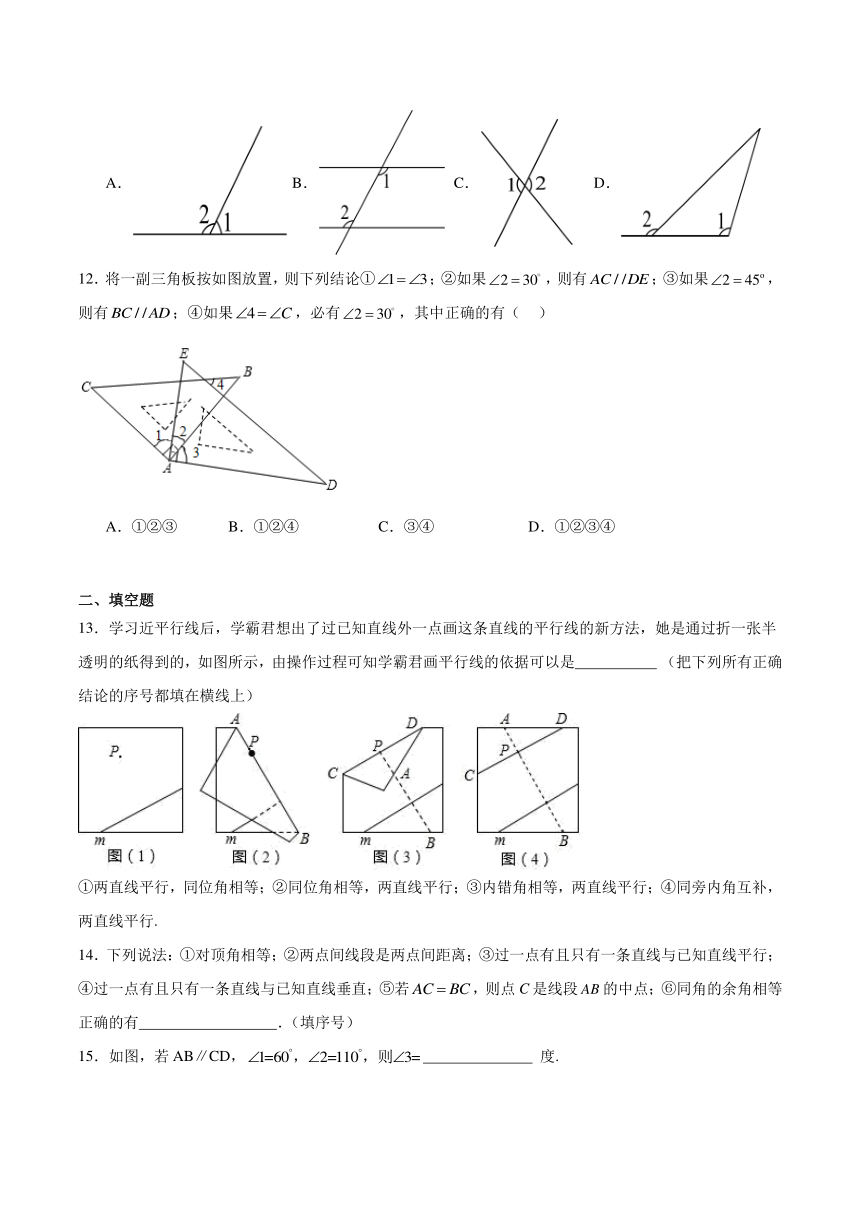
11.下列图形中,一定成立的是( )
A. B. C. D.
12.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
二、填空题
13.学习近平行线后,学霸君想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的,如图所示,由操作过程可知学霸君画平行线的依据可以是 (把下列所有正确结论的序号都填在横线上)
①两直线平行,同位角相等;②同位角相等,两直线平行;③内错角相等,两直线平行;④同旁内角互补,两直线平行.
14.下列说法:①对顶角相等;②两点间线段是两点间距离;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤若,则点C是线段的中点;⑥同角的余角相等正确的有 .(填序号)
15.如图,若AB∥CD, 度.
16.如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是 .
17.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为 .(任意添加一个符合题意的条件即可)
18.将一副三角尺如图放置,,则下列结论中正确的是 .(填序号)①;②;③如果,那么;④如果,那么.
19.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗? (填“合格”或“不合格”).
20.在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线AB、CD,并说出自己做法的依据.小琛、小萱、小冉三位同学的做法如下:
小琛说:“我的做法的依据是内错角相等,两直线平行.”
小萱做法的依据是 .
小冉做法的依据是 .
21.如图,,请添加一个条件: ,使得.
22.如图,点E在AC的延长线上,给出的四个条件:
(1);(2);(3);(4)能判断的有 个.
三、解答题
23.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变).
(1)当∠BAD= °,CDAB.
(2)当∠BAD= °,则三角板ACD有一条边与直角边OB平行.(写出所有可能情况)
24.如图,如果,,,那么与平行吗?与呢?观察下面的解答过程,补充必要的依据或结论.
解:∵(已知),
( )
∴( )
又∵( )
∴( )
∴( )
又∵,
∴( )
∵( )
∴( )
∴( )
25.如图,分别平分和,求证.
26.如图,已知射线与直线交于点O,平分,于点O,.
(1)求证:.
(2)若,求的度数.
27.小明想知道作业纸上两条相交直线,所夹锐角的大小(如图1).但发现其交点不在作业纸内,无法直接测量.小明设计了如下方案(如图2):
①作直线分别交,于点,,以点为顶点,为一边,在直线的右侧作;
②测量的度数即可得到直线,所夹锐角的大小.
问题1:你认为小明的方案可行吗?并说明理由.
问题2:你还有其他方法吗?请在图1中画图说明.(测量工具:直尺、量角器)
28.完成下面的证明.
已知:如图,∠1+∠2=180°,∠3+∠4=180°.
求证:AB∥EF.
证明:∵∠1+∠2=180°,
∴AB∥ ( ).
∵∠3+∠4=180°,
∴ ∥ .
∴AB∥EF( ).
29.已知:如图,∠D=∠A,∠B=∠FCB
求证:ED//CF
30.【操作】在如图的方格纸中(网格线的交点叫格点),按要求画图、填空.
(1)过点A作的垂线,垂足为点D,该垂线经过的一个格点记为点E.
(2)过点E作的平行线,该平行线经过的一个格点记为F;过点B作的平行线,该平行线经过的一个格点记为G.
【发现】与的位置关系为______.
【概括】根据你的发现,概括一条事实或结论:______.
31.如图,点A、B、C、D在正方形网格的格点上,每个小方格的边长都为单位1.
(1)仅用无刻度的直尺完成下列画图.
①过点B画直线平行线交直线于点E;
②过点A画直线的垂线,垂足为点F;
③在直线上求作一点P,使点P到B、D两点的距离之和最小.
(2)比较大小:______(填>、<或=),理由:____________.
32.(1)指出下列各图中的与是同位角、内错角还是同旁内角.
① ② ③ ④
(2)请你归纳:辨认同位角、内错角、同旁内角的方法可以是什么?
答案:
1.解:①两点之间,线段最短,故该说法正确;
②若,则C是线段的中点,错误,因为A、B、C三点不一定在同一直线上,故该说法错误;
③对顶角相等,故该说法正确;
④过直线外一点有且只有一条直线与这条直线平行,故该说法错误;
故正确的2个,
故选:C.
2.∵在同一平面内,两条直线的位置关系只有两种:相交和平行,故①不正确;
∵过直线外一点有且只有一条直线垂直于已知直线.故②不正确;
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.故③正确;
从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离.故④不正确;
过直线外一点,有且只有一条直线与已知直线平行.故⑤不正确;
∴不正确的有①②④⑤四个.
故选:C.
3.A.∵ ,
∴(同旁内角互补,两直线平行),
能判定,故A选项不符合题意.
B. ∵,
∴(内错角相等,两直线平行),
能判定,故B选项不符合题意.
C. ∵,
∴(同位角相等,两直线平行),
能判定,故C选项不符合题意.
D. ∵,
∴(同位角相等,两直线平行),
不能判定,故D选项符合题意.
故选:D
4.A.因为,,所以,所以,由“内错角相等,两直线平行” ,可得,故此项不符合题意;
B.因为且,,所以,由A可得,故此项不符合题意;
C.因为且,所以,由“内错角相等,两直线平行” ,可得,故此项不符合题意;
D.由无法判断,故此项符合题意;
故选:D.
5.解:A、∵,∴,本选项不合题意;
B、∵,∴,本选项不合题意;
C、∵,∴,本选项不合题意;
D、∵,∴,本选项符合题意.
故选:D.
6.解:A、∵,
∴(同旁内角互补,两直线平行),故A不符合题意;
B、∵,
∴(内错角相等,两直线平行),故B不符合题意;
C、∵,
∴(同位角相等,两直线平行),故C不符合题意;
D、根据不能判断直线,故D符合题意;
故选:D.
7.解:如图
∵∠1=∠2=90°
∴∠1+∠2=180°,
∴a//b;
∵∠1=∠3=90°
∴a//b;
∵a⊥c,b⊥c,
∴a//b
故①③④正确;
故选C
8.解:A.在同一平面内,若,则正确,故本选项正确;
B.在同一平面内,若,则,故本选项错误;
C.在同一平面内,若,则,故本选项错误;
D.在同一平面内,若,则,故本选项错误.
故选:A.
9.解:①在同一平面内,如果直线a∥b,a⊥c,那么b⊥c;正确;
②根据平行公理的推论,平行于同一条直线的两条直线平行;故本项正确;
在同一平面内,如果直线b⊥a,c⊥a,那么b∥c;故③错误;④正确;
故选B
10.解:如图,
射线AB和CD被直线AD组成的图形中,同位角有4对,
射线BA和CD被射线BC所截,形成1对同位角;
射线BC和直线AD被射线BA所截,形成1对同位角;
射线BC和直线AD被射线CD所截,形成2对同位角;
则总共有8对同位角
故选:C.
11.解:、和是邻补角,不一定相等,故选项不符合题意;
、和是内错角,不一定相等,故选项不符合题意;
、和是对顶角,根据对顶角的性质可知,故选项符合题意;
、和是同位角,不一定相等,故选项不符合题意;
故选:.
12.∵∠1+∠2=∠3+∠2=90,
∴∠1=∠3,故①正确;
∵,
∴
∠E=60,
∴∠1=∠E,
∴AC∥DE,故②正确;
∵,
∴,
∵,
∴∠3=∠B,
∴,故③正确;
∵,
∴∠CFE=∠C,
∵∠CFE+∠E=∠C+∠1,
∴∠1=∠E=,
∴∠2=90-∠1=,故④正确,
故选:D.
13.由图可知,虚线与其他折痕垂直,根据折后角的关系可得同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,所以选②③④.
故答案为②③④
14.①对顶角相等正确;
②由两点间线段的长度是两点间距离,所以两点间线段是两点间距离不正确;
③由过直线外一点有且只有一条直线与已知直线平行,所以过一点有且只有一条直线与已知直线平行不正确;
④在同一平面内,过一点有且只有一条直线与已知直线垂直,故错误;
⑤由线段中点的性质,若,点C在AB上,则点C是线段的中点,所以若,则点C是线段的中点不正确;
⑥同角的余角相等正确;
正确的有①⑥.
故答案为:①⑥.
15.解:如图,过点E作EF∥AB,
∴∠4=∠1=60°,
∵AB∥CD,
∴EF∥CD,
∴∠2+∠5=180°,
∵∠2=110°,
∴∠5=180°-110°=70°,
∴∠3=180°-∠4-∠5=180°-60°-70°=50°.
故答案为50.
16.∵AB⊥BC,BC⊥CD,
∴∠ABC=∠BCD=90°,
∴AB∥CD,
故答案为AB∥CD.
17.解:若,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD;
故答案为∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(答案不唯一)
18. 解:①,,,
,
,结论①正确;
②,
,结论②正确;
③,
,
又,
,
,结论③正确;
④,
,
又,
,
,结论④正确.
正确的结论有①②③④.
故答案为:①②③④.
19.由题知,∠ABC=120°,∠BCD=60°,所以∠ABC+∠BCD=180°, 得到,AB∥CD. 所以,零件合格.
20.解: 小萱做法的依据是同位角相等两直线平行或同旁内角互补两直线平行;
小冉做法的依据是内错角相等两直线平行或同旁内角互补两直线平行;
故答案为:同位角相等两直线平行或同旁内角互补两直线平行;内错角相等两直线平行或同旁内角互补两直线平行;
21.解:添加EF⊥AB CD⊥AB,
∴∠ADC=∠AFE=90°
∴CD∥EF(同位角相等两直线平行)
故答案为:EF⊥AB
22.(1)如果 ,那么 ,故(1) 错误;
(2),那么 ,内错角相等,两直线平行,故(2)正确;
(3),那么 ; 同位角相等,两直线平行,故(3)正确;
(4),那么 , 同旁内角互补,两直线平行,故(4) 正确;
即正确的有
故答案为:3
23.解:(1)如图所示:当CD∥AB时,∠BAD=∠D=30°;
如图所示,当AB∥CD时,∠C=∠BAC=60°,
∴∠BAD=60°+90°=150°;
故答案为:150或30;
(2)如图所示,当CD∥OB时,∠BAD=45°﹣30°=15°;
如图所示,当AD∥BO时,∠BAD=∠B=45°;
如图所示,当AC∥BO时,∠BAD=45°+90°=135°;
如图所示,当CD∥BO时,∠BAD=180°﹣60°+45°=165°;
如图所示,当AD∥BO时,∠BAD=45°+90°=135°;
如图所示,当AC∥BO时,∠BAD=45°.
综上所述,∠BAD的度数为15°或45°或135°或165°.
故答案为:15或45或135或165.
24.解:∵(已知),
(对顶角相等),
∴(等量代换),
又∵(已知),
∴(等式的性质),
∴(同旁内角互补,两直线平行),
又∵,
∴(补角的定义),
∵(已知),
∴(等式的性质),
∴(内错角相等,两直线平行).
25.证明:,
,
分别平分和,
,
,
.
26.(1)证明:∵,,
∴,
∵平分,
∴,
∴
∴;
(2)解:由(1)可知,,
∵,
∴,
∵,
∴,
∴.
27.问题1:小明的方案可行.
理由:如图,设直线,相交于点.
,
,
.
问题2:如图,在上取点,在上取点,作直线,量出和的大小,利用三角形内角和即可求出直线,所夹锐角的大小.
若和的和是,则说明两直线平行.
28.证明:如图所示:
∵∠1+∠2=180°(已知),
∴AB∥CD(同旁内角互补,两直线平行),
∵∠3+∠4=180°(已知),
∴CD∥EF(同旁内角互补,两直线平行),
∴AB∥EF(若两直线同时平行于第三直线,则这两直线也相互平行),
故答案为:CD;同旁内角互补,两直线平行;CD;EF;若两直线同时平行于第三条直线,则这两条直线也相互平行.
29.证明:∵∠A=∠D
∴DE∥AB
∵∠B=∠BCF
∴AB∥CF
∴DE∥CF
30.解:(1)如图,,D为垂足;
(2)如图,,,
与的位置关系为平行;
结论:平行于同一条直线的两条直线平行.
31.(1)如图,①即为直线平行线,
②即为直线的垂线,
③点P即为所求
(2)∵,
∴(垂线段最短).
故答案为:<,垂线段最短.
32.(1)①与是内错角;②与是同旁内角;③与是同位角;④与是同位角.
故答案为:内错角,同旁内角,同位角,同位角;
(2)辨认同位角、内错角、同旁内角的方法:在截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中主线是截线,抓住了截线,再利用图形结构特征,同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形进行判断.
同步练习(含答案)
姓名:___________班级:___________考号:___________
一、单选题
1.对于下列四个说法:①两点之间,线段最短;②若,则C是线段的中点;③对顶角相等;④过一点有且只有一条直线与这条直线平行,其中,正确的有( )
A.0个 B.1个 C.2个 D.3个
2.下列说法中不正确的个数为( ).
①在同一平面内,两条直线的位置关系只有两种:相交和垂直.
②有且只有一条直线垂直于已知直线.
③如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
④从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.
⑤过一点,有且只有一条直线与已知直线平行.
A.2个 B.3个 C.4个 D.5个
3.如图,在下列给出的条件中,不能判定的是( )
A. B.
C. D.
4.如图,、分别在和内部,若,则下列条件中,不能判定的是( )
A. B.且
C.且 D.
(3题) (4题)
5.如图,点E在的延长线上,则下列条件中不能判定的是( )
A. B.
C. D.
6.如图,下列条件中,不能判断直线的是( )
A. B. C. D.
(5题) (6题)
7.如图,木工师傅在一块木板上画两条平行线,方法是:用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:其中正确的是( )
①同位角相等,两直线平行; ②内错角相等,两直线平行;
③同旁内角互补,两直线平行; ④平面内垂直于同一直线的两条直线平行.
A.①②③ B.①②④ C.①③④ D.①③
8.在同一平面内,a、b、c是直线,下列说法正确的是( )
A.若, 则 B.若,,则
C.若,,则 D.若,,则
9.已知三条不同的直线a,b,c在同一平面内,下列说法正确的个数是( )
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
A.2个 B.3个 C.4个 D.0个
10.如图所示,图中同位角共有( )
A.4对 B.6对 C.8对 D.10对
11.下列图形中,一定成立的是( )
A. B. C. D.
12.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
二、填空题
13.学习近平行线后,学霸君想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的,如图所示,由操作过程可知学霸君画平行线的依据可以是 (把下列所有正确结论的序号都填在横线上)
①两直线平行,同位角相等;②同位角相等,两直线平行;③内错角相等,两直线平行;④同旁内角互补,两直线平行.
14.下列说法:①对顶角相等;②两点间线段是两点间距离;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤若,则点C是线段的中点;⑥同角的余角相等正确的有 .(填序号)
15.如图,若AB∥CD, 度.
16.如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是 .
17.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为 .(任意添加一个符合题意的条件即可)
18.将一副三角尺如图放置,,则下列结论中正确的是 .(填序号)①;②;③如果,那么;④如果,那么.
19.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗? (填“合格”或“不合格”).
20.在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线AB、CD,并说出自己做法的依据.小琛、小萱、小冉三位同学的做法如下:
小琛说:“我的做法的依据是内错角相等,两直线平行.”
小萱做法的依据是 .
小冉做法的依据是 .
21.如图,,请添加一个条件: ,使得.
22.如图,点E在AC的延长线上,给出的四个条件:
(1);(2);(3);(4)能判断的有 个.
三、解答题
23.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变).
(1)当∠BAD= °,CDAB.
(2)当∠BAD= °,则三角板ACD有一条边与直角边OB平行.(写出所有可能情况)
24.如图,如果,,,那么与平行吗?与呢?观察下面的解答过程,补充必要的依据或结论.
解:∵(已知),
( )
∴( )
又∵( )
∴( )
∴( )
又∵,
∴( )
∵( )
∴( )
∴( )
25.如图,分别平分和,求证.
26.如图,已知射线与直线交于点O,平分,于点O,.
(1)求证:.
(2)若,求的度数.
27.小明想知道作业纸上两条相交直线,所夹锐角的大小(如图1).但发现其交点不在作业纸内,无法直接测量.小明设计了如下方案(如图2):
①作直线分别交,于点,,以点为顶点,为一边,在直线的右侧作;
②测量的度数即可得到直线,所夹锐角的大小.
问题1:你认为小明的方案可行吗?并说明理由.
问题2:你还有其他方法吗?请在图1中画图说明.(测量工具:直尺、量角器)
28.完成下面的证明.
已知:如图,∠1+∠2=180°,∠3+∠4=180°.
求证:AB∥EF.
证明:∵∠1+∠2=180°,
∴AB∥ ( ).
∵∠3+∠4=180°,
∴ ∥ .
∴AB∥EF( ).
29.已知:如图,∠D=∠A,∠B=∠FCB
求证:ED//CF
30.【操作】在如图的方格纸中(网格线的交点叫格点),按要求画图、填空.
(1)过点A作的垂线,垂足为点D,该垂线经过的一个格点记为点E.
(2)过点E作的平行线,该平行线经过的一个格点记为F;过点B作的平行线,该平行线经过的一个格点记为G.
【发现】与的位置关系为______.
【概括】根据你的发现,概括一条事实或结论:______.
31.如图,点A、B、C、D在正方形网格的格点上,每个小方格的边长都为单位1.
(1)仅用无刻度的直尺完成下列画图.
①过点B画直线平行线交直线于点E;
②过点A画直线的垂线,垂足为点F;
③在直线上求作一点P,使点P到B、D两点的距离之和最小.
(2)比较大小:______(填>、<或=),理由:____________.
32.(1)指出下列各图中的与是同位角、内错角还是同旁内角.
① ② ③ ④
(2)请你归纳:辨认同位角、内错角、同旁内角的方法可以是什么?
答案:
1.解:①两点之间,线段最短,故该说法正确;
②若,则C是线段的中点,错误,因为A、B、C三点不一定在同一直线上,故该说法错误;
③对顶角相等,故该说法正确;
④过直线外一点有且只有一条直线与这条直线平行,故该说法错误;
故正确的2个,
故选:C.
2.∵在同一平面内,两条直线的位置关系只有两种:相交和平行,故①不正确;
∵过直线外一点有且只有一条直线垂直于已知直线.故②不正确;
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.故③正确;
从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离.故④不正确;
过直线外一点,有且只有一条直线与已知直线平行.故⑤不正确;
∴不正确的有①②④⑤四个.
故选:C.
3.A.∵ ,
∴(同旁内角互补,两直线平行),
能判定,故A选项不符合题意.
B. ∵,
∴(内错角相等,两直线平行),
能判定,故B选项不符合题意.
C. ∵,
∴(同位角相等,两直线平行),
能判定,故C选项不符合题意.
D. ∵,
∴(同位角相等,两直线平行),
不能判定,故D选项符合题意.
故选:D
4.A.因为,,所以,所以,由“内错角相等,两直线平行” ,可得,故此项不符合题意;
B.因为且,,所以,由A可得,故此项不符合题意;
C.因为且,所以,由“内错角相等,两直线平行” ,可得,故此项不符合题意;
D.由无法判断,故此项符合题意;
故选:D.
5.解:A、∵,∴,本选项不合题意;
B、∵,∴,本选项不合题意;
C、∵,∴,本选项不合题意;
D、∵,∴,本选项符合题意.
故选:D.
6.解:A、∵,
∴(同旁内角互补,两直线平行),故A不符合题意;
B、∵,
∴(内错角相等,两直线平行),故B不符合题意;
C、∵,
∴(同位角相等,两直线平行),故C不符合题意;
D、根据不能判断直线,故D符合题意;
故选:D.
7.解:如图
∵∠1=∠2=90°
∴∠1+∠2=180°,
∴a//b;
∵∠1=∠3=90°
∴a//b;
∵a⊥c,b⊥c,
∴a//b
故①③④正确;
故选C
8.解:A.在同一平面内,若,则正确,故本选项正确;
B.在同一平面内,若,则,故本选项错误;
C.在同一平面内,若,则,故本选项错误;
D.在同一平面内,若,则,故本选项错误.
故选:A.
9.解:①在同一平面内,如果直线a∥b,a⊥c,那么b⊥c;正确;
②根据平行公理的推论,平行于同一条直线的两条直线平行;故本项正确;
在同一平面内,如果直线b⊥a,c⊥a,那么b∥c;故③错误;④正确;
故选B
10.解:如图,
射线AB和CD被直线AD组成的图形中,同位角有4对,
射线BA和CD被射线BC所截,形成1对同位角;
射线BC和直线AD被射线BA所截,形成1对同位角;
射线BC和直线AD被射线CD所截,形成2对同位角;
则总共有8对同位角
故选:C.
11.解:、和是邻补角,不一定相等,故选项不符合题意;
、和是内错角,不一定相等,故选项不符合题意;
、和是对顶角,根据对顶角的性质可知,故选项符合题意;
、和是同位角,不一定相等,故选项不符合题意;
故选:.
12.∵∠1+∠2=∠3+∠2=90,
∴∠1=∠3,故①正确;
∵,
∴
∠E=60,
∴∠1=∠E,
∴AC∥DE,故②正确;
∵,
∴,
∵,
∴∠3=∠B,
∴,故③正确;
∵,
∴∠CFE=∠C,
∵∠CFE+∠E=∠C+∠1,
∴∠1=∠E=,
∴∠2=90-∠1=,故④正确,
故选:D.
13.由图可知,虚线与其他折痕垂直,根据折后角的关系可得同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,所以选②③④.
故答案为②③④
14.①对顶角相等正确;
②由两点间线段的长度是两点间距离,所以两点间线段是两点间距离不正确;
③由过直线外一点有且只有一条直线与已知直线平行,所以过一点有且只有一条直线与已知直线平行不正确;
④在同一平面内,过一点有且只有一条直线与已知直线垂直,故错误;
⑤由线段中点的性质,若,点C在AB上,则点C是线段的中点,所以若,则点C是线段的中点不正确;
⑥同角的余角相等正确;
正确的有①⑥.
故答案为:①⑥.
15.解:如图,过点E作EF∥AB,
∴∠4=∠1=60°,
∵AB∥CD,
∴EF∥CD,
∴∠2+∠5=180°,
∵∠2=110°,
∴∠5=180°-110°=70°,
∴∠3=180°-∠4-∠5=180°-60°-70°=50°.
故答案为50.
16.∵AB⊥BC,BC⊥CD,
∴∠ABC=∠BCD=90°,
∴AB∥CD,
故答案为AB∥CD.
17.解:若,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD;
故答案为∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(答案不唯一)
18. 解:①,,,
,
,结论①正确;
②,
,结论②正确;
③,
,
又,
,
,结论③正确;
④,
,
又,
,
,结论④正确.
正确的结论有①②③④.
故答案为:①②③④.
19.由题知,∠ABC=120°,∠BCD=60°,所以∠ABC+∠BCD=180°, 得到,AB∥CD. 所以,零件合格.
20.解: 小萱做法的依据是同位角相等两直线平行或同旁内角互补两直线平行;
小冉做法的依据是内错角相等两直线平行或同旁内角互补两直线平行;
故答案为:同位角相等两直线平行或同旁内角互补两直线平行;内错角相等两直线平行或同旁内角互补两直线平行;
21.解:添加EF⊥AB CD⊥AB,
∴∠ADC=∠AFE=90°
∴CD∥EF(同位角相等两直线平行)
故答案为:EF⊥AB
22.(1)如果 ,那么 ,故(1) 错误;
(2),那么 ,内错角相等,两直线平行,故(2)正确;
(3),那么 ; 同位角相等,两直线平行,故(3)正确;
(4),那么 , 同旁内角互补,两直线平行,故(4) 正确;
即正确的有
故答案为:3
23.解:(1)如图所示:当CD∥AB时,∠BAD=∠D=30°;
如图所示,当AB∥CD时,∠C=∠BAC=60°,
∴∠BAD=60°+90°=150°;
故答案为:150或30;
(2)如图所示,当CD∥OB时,∠BAD=45°﹣30°=15°;
如图所示,当AD∥BO时,∠BAD=∠B=45°;
如图所示,当AC∥BO时,∠BAD=45°+90°=135°;
如图所示,当CD∥BO时,∠BAD=180°﹣60°+45°=165°;
如图所示,当AD∥BO时,∠BAD=45°+90°=135°;
如图所示,当AC∥BO时,∠BAD=45°.
综上所述,∠BAD的度数为15°或45°或135°或165°.
故答案为:15或45或135或165.
24.解:∵(已知),
(对顶角相等),
∴(等量代换),
又∵(已知),
∴(等式的性质),
∴(同旁内角互补,两直线平行),
又∵,
∴(补角的定义),
∵(已知),
∴(等式的性质),
∴(内错角相等,两直线平行).
25.证明:,
,
分别平分和,
,
,
.
26.(1)证明:∵,,
∴,
∵平分,
∴,
∴
∴;
(2)解:由(1)可知,,
∵,
∴,
∵,
∴,
∴.
27.问题1:小明的方案可行.
理由:如图,设直线,相交于点.
,
,
.
问题2:如图,在上取点,在上取点,作直线,量出和的大小,利用三角形内角和即可求出直线,所夹锐角的大小.
若和的和是,则说明两直线平行.
28.证明:如图所示:
∵∠1+∠2=180°(已知),
∴AB∥CD(同旁内角互补,两直线平行),
∵∠3+∠4=180°(已知),
∴CD∥EF(同旁内角互补,两直线平行),
∴AB∥EF(若两直线同时平行于第三直线,则这两直线也相互平行),
故答案为:CD;同旁内角互补,两直线平行;CD;EF;若两直线同时平行于第三条直线,则这两条直线也相互平行.
29.证明:∵∠A=∠D
∴DE∥AB
∵∠B=∠BCF
∴AB∥CF
∴DE∥CF
30.解:(1)如图,,D为垂足;
(2)如图,,,
与的位置关系为平行;
结论:平行于同一条直线的两条直线平行.
31.(1)如图,①即为直线平行线,
②即为直线的垂线,
③点P即为所求
(2)∵,
∴(垂线段最短).
故答案为:<,垂线段最短.
32.(1)①与是内错角;②与是同旁内角;③与是同位角;④与是同位角.
故答案为:内错角,同旁内角,同位角,同位角;
(2)辨认同位角、内错角、同旁内角的方法:在截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中主线是截线,抓住了截线,再利用图形结构特征,同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形进行判断.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
