苏科版2023-2024学年 七年级下册数学 7.4认识三角形同步练习(含答案)
文档属性
| 名称 | 苏科版2023-2024学年 七年级下册数学 7.4认识三角形同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 00:00:00 | ||
图片预览


文档简介
苏科版2023-2024学年七年级下册数学7.4认识三角形
同步练习(含答案)
姓名:___________班级:___________考号:___________
一、单选题
1.一个长为19cm,宽为18cm的长方形,如果把这个长方形分成若干个正方形要求正方形的边长为正整数,那么该长方形最少可分成正方形的个数( )
A.5个 B.6个 C.7个 D.8个
2.下列说法正确的是( )
A.所有的等腰三角形都是锐角三角形
B.等边三角形属于等腰三角形
C.不存在既是钝角三角形又是等腰三角形的三角形
D.一个三角形里有两个锐角,则一定是锐角三角形
3.如图所示,则△ABC的形状是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
4.已知三角形的两边长分别为3cm和8cm,则此三角形的第三边的长可能是( )
A.13cm B.6cm C.5cm D.4cm
5.如图,嘉琪任意剪了一张钝角三角形纸片(是钝角),他打算用折叠的方法折出的角平分线、边上的中线和高线,能折出的是( )
A.边上的中线和高线 B.的角平分线和边上的高线
C.的角平分线和边上的中线 D.的角平分线、边上的中线和高线
6.小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
A.AB,AC边上的中线的交点 B.AB,AC边上的垂直平分线的交点
C.AB,AC边上的高所在直线的交点 D.∠BAC与∠ABC的角平分线的交点
7.三角形的中线将三角形分成面积相等的两部分,如果两个三角形的高相同,则它们的面积比等于对应底边的比.如图①,△MBC中,M是BC上一点,则有,如图②,△ABC中,M是BC上一点,且BM=BC,N是AC的中点,若△ABC的面积是1,则△ADN的面积是( )
A. B. C. D.
8.如图,在中,,是内角的平分线,是外角的平分线,是外角的平分线,以下结论不正确的是( )
A. B.
C. D.平分
9.如图,是的高,是的角平分线,若,,则的度数是( )
A. B. C. D.
(8题) (9题)
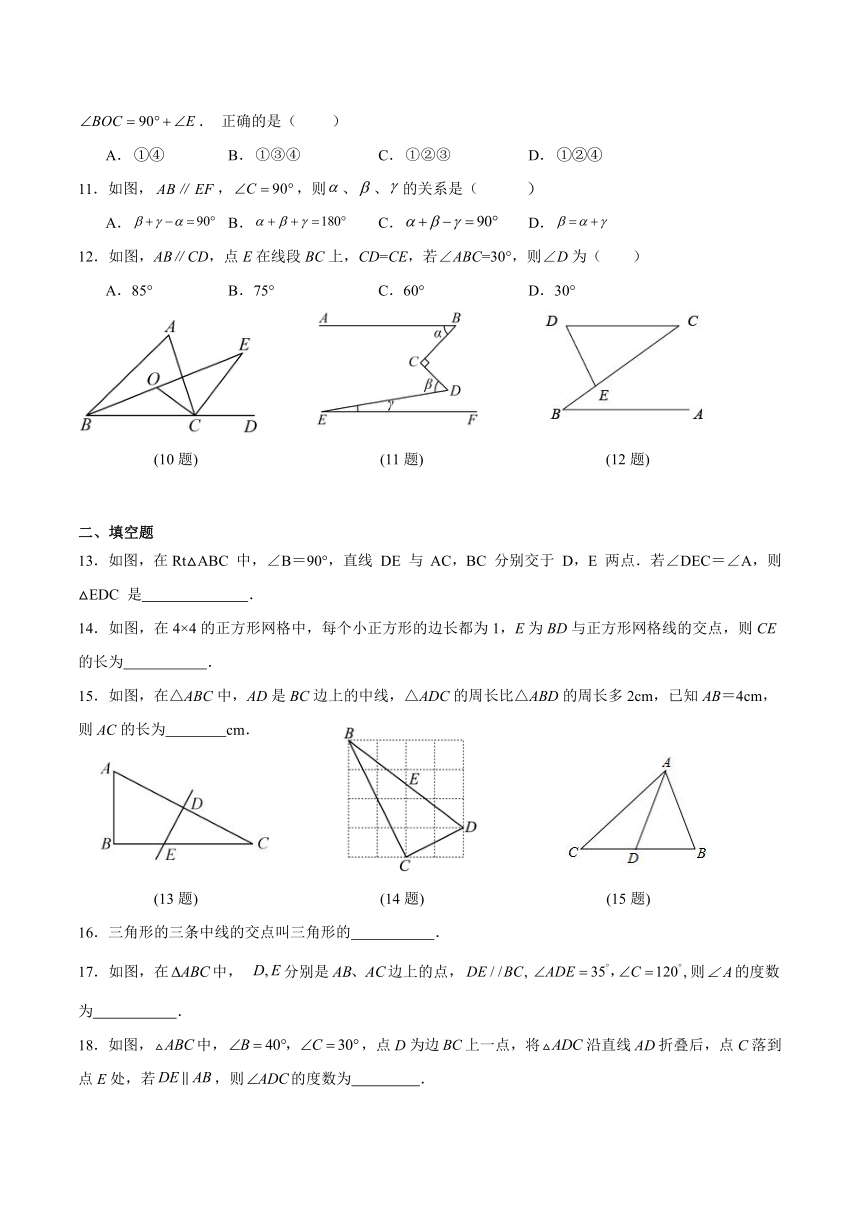
10.如图,在中,,分别平分,,且交于点,为外角的平分线,的延长线交于点, 则以下结论: ;; ; . 正确的是( )
A. B. C. D.
11.如图,,,则、、的关系是( )
A. B. C. D.
12.如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D为( )
A.85° B.75° C.60° D.30°
(10题) (11题) (12题)
二、填空题
13.如图,在Rt△ABC 中,∠B=90°,直线 DE 与 AC,BC 分别交于 D,E 两点.若∠DEC=∠A,则△EDC 是 .
14.如图,在4×4的正方形网格中,每个小正方形的边长都为1,E为BD与正方形网格线的交点,则CE的长为 .
15.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多2cm,已知AB=4cm,则AC的长为 cm.
(13题) (14题) (15题)
16.三角形的三条中线的交点叫三角形的 .
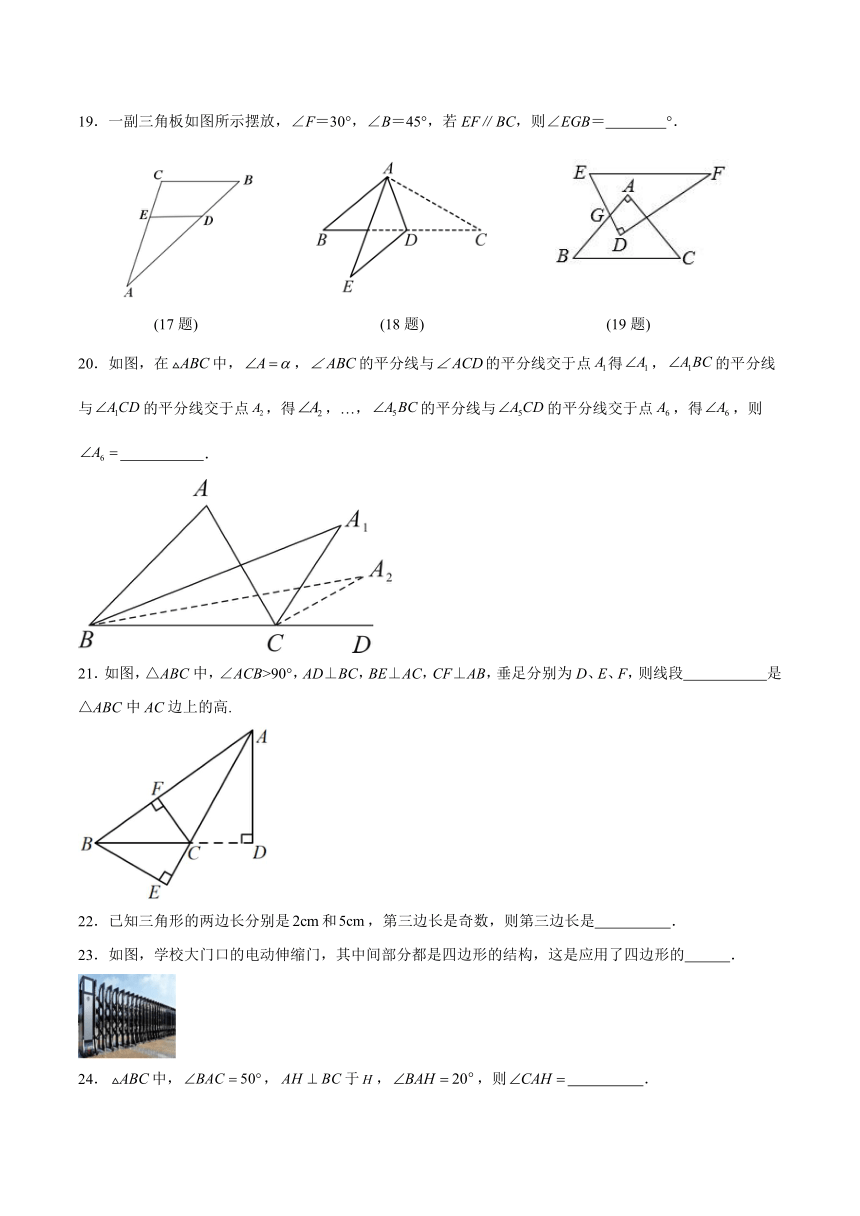
17.如图,在中, 分别是边上的点,则的度数为 .
18.如图,中,,点D为边上一点,将沿直线折叠后,点C落到点E处,若,则的度数为 .
19.一副三角板如图所示摆放,∠F=30°,∠B=45°,若EFBC,则∠EGB= °.
(17题) (18题) (19题)
20.如图,在中,,的平分线与的平分线交于点得,的平分线与的平分线交于点,得,…,的平分线与的平分线交于点,得,则 .
21.如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则线段 是△ABC中AC边上的高.
22.已知三角形的两边长分别是和,第三边长是奇数,则第三边长是 .
23.如图,学校大门口的电动伸缩门,其中间部分都是四边形的结构,这是应用了四边形的 .
24.中,,于,,则 .
25.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以为公共边的“共边三角形”有 对.
26.如图是用一副七巧板拼成的正方形,边长是10cm.图中小正方形(涂色部分)的面积是 .
27.如图,为了使木门不变形,木工师傅在木门上加钉了一根木条,这样是利用三角形的 .
28.五条线段的长度分别为1cm,2cm,3cm,4cm,5cm,以其中三条线段为边长共可以组成 个三角形.
三、解答题
29.动手做一做:某校教具制作车间有等腰三角形正方形、平行四边形的塑料若干,数学兴趣小组的同学利用其中7块恰好拼成一个矩形(如图1),后来又用它们拼出了XYZ等字母模型(如图2、图3、图4),每个塑料板保持图1的标号不变,请你参与:
(1)将图2中每块塑料板对应的标号填上去;
(2)图3中,只画出了标号7的塑料板位置,请你适当画线,找出其他6块塑料板, 并填上标号;
(3)在图4中,找出7块塑料板,并填上标号.
30.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个边形木架在同一平面内不变形,至少还要再钉上几根木条?
31.如图,草原上有四口油井,位于四边形ABCD的四个顶点上,现在要建立一个维修站H,试问H建在何处,才能使它到四口油井的距离之和最小,说明理由
32.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)请画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两条线段之间的关系是 ;
(3)利用网格画出△ABC 中AC边上的中线BD;
(4)利用网格画出△ABC 中AB边上的高CE;
(5)△A′B′C′的面积为 .
33.如图,在中,为边上的高,点为边上的一点,连接.
(1)当为边上的中线时,若,的面积为24,求的长;
(2)当为的角平分线时,若,,求的度数.
34.如图,已知,分别是的高和中线,,,,.试求:
(1)的长;
(2)的面积;
(3)和的周长差.
35.作图题:(利用无刻度的直尺作图)
如图,在方格纸中,有两条线段.利用方格纸完成以下操作:
(1)过点A作的平行线;
(2)过点C作的平行线,与(1)中的平行线交于点D;
(3)过点B作的垂线;
(4)请在上找一点P,使得线段平分三角形的面积,在图上作出线段.
36.如图,与分别是的角平分线和高.若,,求度数.
37.如图,三角形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的三角形叫做格点三角形.在8×8网格中有一个格点三角形ABC,按要求解答下列各题:
(1)画出△ABC向上平移3格后得到的△;
(2)若每个小正方形边长为1,求△的面积.
38.如图,点在上,点在上,,交于点,且,,求的度数.
39.如图,DE∥BC将△ADE沿着DE对折,点A落在BC边的点F上,若∠B=50o,求∠BDF的度数.
40.如图,中,,是边上的高,求的度数.
答案:
1.根据正方形的边长为正整数的特点,可知长为19cm,宽为18cm的长方形,分成若干个正方形,上面两个正方形从左至右为11和8,8下面从左至右是3和5,最下面一排从左至右是7,7,5时正方形的个数最少.
7个正方形边长分别11,8,7,7,5,5,3.
故选:C.
2.A选项:内角为30°,30°,120°的等腰三角形是钝角三角形,故是错误的.
B选项:等边三角形属于等腰三角形,故正确.
C选项:内角为30°,30°,120°的三角形既是钝角三角形又是等腰三角形的三角形,故错误.
D选项:内角为30°,30°,120°的三角形有两个锐角,是钝角三角形,故错误.
故选B.
3.∠A+∠B+∠C=180°,
因为∠A=β,∠B=2β,
所以∠A+∠B=3β=∠C=90°,
△ABC的形状是直角三角形.
故选C.
4.解:第三边长x的范围是:,即,
故选:B.
5.解:当与重合时,折痕是的角平分线;
当点A与点B重合时,折叠是的中垂线,
故选:C.
6.本题实质上是要确定三角形外接圆的圆心,三角形外接圆的圆心是三边垂直平分线的交点,
故选B.
7.解:连接CD,如图:
∵N是AC的中点,
∴==1,
∴S△ADN=S△CDN,
同理:S△ABN=S△CBN,
设S△ADN=S△CDN=a,
∵△ABC的面积是1,
∴S△ABN=S△CBN=,
∴S△BCD=S△ABD=﹣a,
∵BM=BC,
∴=,
∴==,==,
∴S△CDM=3S△BDM,S△ACM=3S△ABM,
∴S△CDM=S△BCD=×(﹣a)=﹣a,S△ACM=S△ABC=,
∵S△ACM=S四边形CMDN+S△ADN=S△CDM+S△CDN+S△ADN,
即:=﹣a+a+a,
解得:a=,
∴S△ADN=,
故选:B.
8.A. ∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故A正确.
B. 由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故B正确.
C. 在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90° ∠ABD,
故C正确;
D. ∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90° ∠ABC,
∴∠ADB不等于∠CDB,∴D错误;
故选D.
9.解:∵,,
∴,
∵平分,
∴,
∵是的边上的高,
∴,
∵,
∴,
∴,
故选:A.
10.解:∵为外角的平分线,平分,
∴,,
又∵是的外角,
∴,
故正确,
∵,分别平分,
∴,,
∴
,
故错误,
∵平分,平分,
∴,,
∴,
∴是的外角,
∴,
故正确,
综上所述正确的结论是,
故选:.
11.解:延长交于,延长交于,如图,
,
在直角中,;
在中,,
,
,
,
;
故选:C.
12.∵AB∥CD,
∴∠C=∠ABC=30°,
又∵CD=CE,
∴∠D=∠CED,
∵∠C+∠D+∠CED=180°,即30°+2∠D=180°,
∴∠D=75°.
故选B.
13.解: 在Rt△ABC 中,
∵∠B=90°,
∴∠A+∠C=90°,
∵∠DEC=∠A,
∴∠DEC+∠C=90°,
∴∠EDC=90°,
∴△EDC 是直角三角形,
故答案为 直角三角形.
14.取网格点M、N,如图,
结合网格,利用割补法,可得:,
∵,
∴,
∵,,
∴,
∴,
∴,
故答案为:.
15. AD是BC边上的中线
CD= BD
△ADC的周长比△ABD的周长多2cm
(AC+ CD+ AD)-(AD+ DB+ AB)= 2cm
AC - AB = 2cm
AB = 4cm
AC = 6cm
故答案为:6.
16.解:三角形的三条中线的交点叫三角形的重心,
故答案为:重心.
17.解:∵DE∥BC,∠ADE=35°,
∴∠ADE=∠B=35°,
∵∠C=120°,∠A+∠B+∠C=180°,
∴∠A=180°-∠B-∠C=180°-35°-120°=25°.
故答案是:25°.
18.∵,
∴,
由折叠的性质得,,
∵,
∴,
∴,
∴,
故答案为:.
19.解:如图,延长交于点,
,
,
,
,
又,
,
故答案为:105.
20.解;∵平分,平分,
∴,,
∵由三角形外角的性质可得,,
∴,
以此类推,
,
……
∴,
故答案为:.
21.根据图形可得,BE是△ABC中AC边上的高.
故答案为:BE.
22.解:∵,
∴3<第三边<7,
∵第三边为奇数,
∴第三边长为.
故答案为:.
23.解:学校大门做成伸缩门,这是应用了四边形不稳定性的特性.
故答案为:不稳定性.
24.解:分两种情况讨论:
当是锐角三角形时,如图,
于,,
;
当是钝角三角形时,如图,
于,,
;
综上所述,或,
故答案为:或.
25.解:以为公共边的“共边三角形”有与、与、与共3对.
故答案为:3.
26.解:正方形的面积为10×10=100()
∴100÷4÷2=12.5()
∴涂色正方形的面积是12.5.
故答案为:12.5.
27.解:在木门上加钉了一根木条,把一个四边形分成了两个三角形,
这样做的道理是三角形具有稳定性.
故答案为:稳定性.
28.根据三角形的三边关系可知,以其中三条线段为边长,可以组成三角形的是:
2cm、3cm、4cm;3cm、4cm、5cm;2cm、4cm、5cm.
共3个三角形.
故答案为3
29.(1)如下图
(2)如下图
(3)如下图
30.解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上根木条;
要使一个边形木架不变形,至少再钉上根木条.
31.解:H建在、的交点处,理由如下:
连接、相交于点H,任取一点,连接、、、,
在中,,
在中,,
,
,
,
最小,
即维修站H建在、的交点处,才能使它到四口油井的距离之和最小.
32.试题分析:(1)利用平移变换的性质得出对应点位置进而得出答案;
(2)利用平移变换的性质得出答案;
(3)利用网格结合三角形中线的性质得出答案;
(4)利用网格结合三角形高线的性质得出答案;
(5)利用平移的性质结合三角形面积求法得出答案.
解:(1)如图所示:△A′B′C′即为所求;
(2)连接AA′,CC′,则这两条线段之间的关系是平行且相等.
故答案为平行且相等;
(3)如图所示:BD即为所求;
(4)如图所示:CE即为所求;
(5)△A′B′C′的面积为△ABC的面积:×5×4=10.
故答案为10.
33.(1)解:是边上的高,,的面积为24,
,
为边上的中线,
是的中点,
.
(2)解:为边的高,
,.
.
为的角平分线,
,
.
34.(1)解:∵,是边上的高,
∴ ,
∴,
即的长度为;
(2)解:如图,∵是直角三角形,,,,
∴,
又∵是边的中线,
∴,
∴,即,
∴.
∴的面积是;
(3)解:∵是边的中线,
∴,
∴的周长﹣的周长 ,
即和的周长的差是.
35.(1)解:如图,直线即为所作;
;
(2)解:如图,直线即为所作;
(3)解:如图,直线即为所作;
(4)解:如图,线段即为所作.
36.解:∵,
∴ .
∵,
∴.
∵,,
∴.
∵为的角平分线,
∴.
∴.
37.(1)解:如图,△即为所求.
(2)解:△的面积=2.
即△的面积为2.
38.解:∵,
∴,
∵,
∴,
∴,
解得:.
39.∵DE∥BC,
∴∠ADE=∠B=50°;
由题意得:∠FDE=∠ADE=50°,
∴∠BDF=180°-2×50°=80°.
40.解:∵,,
∴,
∴,
∴,
∵是边上的高,
∴,
∴.
同步练习(含答案)
姓名:___________班级:___________考号:___________
一、单选题
1.一个长为19cm,宽为18cm的长方形,如果把这个长方形分成若干个正方形要求正方形的边长为正整数,那么该长方形最少可分成正方形的个数( )
A.5个 B.6个 C.7个 D.8个
2.下列说法正确的是( )
A.所有的等腰三角形都是锐角三角形
B.等边三角形属于等腰三角形
C.不存在既是钝角三角形又是等腰三角形的三角形
D.一个三角形里有两个锐角,则一定是锐角三角形
3.如图所示,则△ABC的形状是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
4.已知三角形的两边长分别为3cm和8cm,则此三角形的第三边的长可能是( )
A.13cm B.6cm C.5cm D.4cm
5.如图,嘉琪任意剪了一张钝角三角形纸片(是钝角),他打算用折叠的方法折出的角平分线、边上的中线和高线,能折出的是( )
A.边上的中线和高线 B.的角平分线和边上的高线
C.的角平分线和边上的中线 D.的角平分线、边上的中线和高线
6.小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
A.AB,AC边上的中线的交点 B.AB,AC边上的垂直平分线的交点
C.AB,AC边上的高所在直线的交点 D.∠BAC与∠ABC的角平分线的交点
7.三角形的中线将三角形分成面积相等的两部分,如果两个三角形的高相同,则它们的面积比等于对应底边的比.如图①,△MBC中,M是BC上一点,则有,如图②,△ABC中,M是BC上一点,且BM=BC,N是AC的中点,若△ABC的面积是1,则△ADN的面积是( )
A. B. C. D.
8.如图,在中,,是内角的平分线,是外角的平分线,是外角的平分线,以下结论不正确的是( )
A. B.
C. D.平分
9.如图,是的高,是的角平分线,若,,则的度数是( )
A. B. C. D.
(8题) (9题)
10.如图,在中,,分别平分,,且交于点,为外角的平分线,的延长线交于点, 则以下结论: ;; ; . 正确的是( )
A. B. C. D.
11.如图,,,则、、的关系是( )
A. B. C. D.
12.如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D为( )
A.85° B.75° C.60° D.30°
(10题) (11题) (12题)
二、填空题
13.如图,在Rt△ABC 中,∠B=90°,直线 DE 与 AC,BC 分别交于 D,E 两点.若∠DEC=∠A,则△EDC 是 .
14.如图,在4×4的正方形网格中,每个小正方形的边长都为1,E为BD与正方形网格线的交点,则CE的长为 .
15.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多2cm,已知AB=4cm,则AC的长为 cm.
(13题) (14题) (15题)
16.三角形的三条中线的交点叫三角形的 .
17.如图,在中, 分别是边上的点,则的度数为 .
18.如图,中,,点D为边上一点,将沿直线折叠后,点C落到点E处,若,则的度数为 .
19.一副三角板如图所示摆放,∠F=30°,∠B=45°,若EFBC,则∠EGB= °.
(17题) (18题) (19题)
20.如图,在中,,的平分线与的平分线交于点得,的平分线与的平分线交于点,得,…,的平分线与的平分线交于点,得,则 .
21.如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则线段 是△ABC中AC边上的高.
22.已知三角形的两边长分别是和,第三边长是奇数,则第三边长是 .
23.如图,学校大门口的电动伸缩门,其中间部分都是四边形的结构,这是应用了四边形的 .
24.中,,于,,则 .
25.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以为公共边的“共边三角形”有 对.
26.如图是用一副七巧板拼成的正方形,边长是10cm.图中小正方形(涂色部分)的面积是 .
27.如图,为了使木门不变形,木工师傅在木门上加钉了一根木条,这样是利用三角形的 .
28.五条线段的长度分别为1cm,2cm,3cm,4cm,5cm,以其中三条线段为边长共可以组成 个三角形.
三、解答题
29.动手做一做:某校教具制作车间有等腰三角形正方形、平行四边形的塑料若干,数学兴趣小组的同学利用其中7块恰好拼成一个矩形(如图1),后来又用它们拼出了XYZ等字母模型(如图2、图3、图4),每个塑料板保持图1的标号不变,请你参与:
(1)将图2中每块塑料板对应的标号填上去;
(2)图3中,只画出了标号7的塑料板位置,请你适当画线,找出其他6块塑料板, 并填上标号;
(3)在图4中,找出7块塑料板,并填上标号.
30.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个边形木架在同一平面内不变形,至少还要再钉上几根木条?
31.如图,草原上有四口油井,位于四边形ABCD的四个顶点上,现在要建立一个维修站H,试问H建在何处,才能使它到四口油井的距离之和最小,说明理由
32.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)请画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两条线段之间的关系是 ;
(3)利用网格画出△ABC 中AC边上的中线BD;
(4)利用网格画出△ABC 中AB边上的高CE;
(5)△A′B′C′的面积为 .
33.如图,在中,为边上的高,点为边上的一点,连接.
(1)当为边上的中线时,若,的面积为24,求的长;
(2)当为的角平分线时,若,,求的度数.
34.如图,已知,分别是的高和中线,,,,.试求:
(1)的长;
(2)的面积;
(3)和的周长差.
35.作图题:(利用无刻度的直尺作图)
如图,在方格纸中,有两条线段.利用方格纸完成以下操作:
(1)过点A作的平行线;
(2)过点C作的平行线,与(1)中的平行线交于点D;
(3)过点B作的垂线;
(4)请在上找一点P,使得线段平分三角形的面积,在图上作出线段.
36.如图,与分别是的角平分线和高.若,,求度数.
37.如图,三角形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的三角形叫做格点三角形.在8×8网格中有一个格点三角形ABC,按要求解答下列各题:
(1)画出△ABC向上平移3格后得到的△;
(2)若每个小正方形边长为1,求△的面积.
38.如图,点在上,点在上,,交于点,且,,求的度数.
39.如图,DE∥BC将△ADE沿着DE对折,点A落在BC边的点F上,若∠B=50o,求∠BDF的度数.
40.如图,中,,是边上的高,求的度数.
答案:
1.根据正方形的边长为正整数的特点,可知长为19cm,宽为18cm的长方形,分成若干个正方形,上面两个正方形从左至右为11和8,8下面从左至右是3和5,最下面一排从左至右是7,7,5时正方形的个数最少.
7个正方形边长分别11,8,7,7,5,5,3.
故选:C.
2.A选项:内角为30°,30°,120°的等腰三角形是钝角三角形,故是错误的.
B选项:等边三角形属于等腰三角形,故正确.
C选项:内角为30°,30°,120°的三角形既是钝角三角形又是等腰三角形的三角形,故错误.
D选项:内角为30°,30°,120°的三角形有两个锐角,是钝角三角形,故错误.
故选B.
3.∠A+∠B+∠C=180°,
因为∠A=β,∠B=2β,
所以∠A+∠B=3β=∠C=90°,
△ABC的形状是直角三角形.
故选C.
4.解:第三边长x的范围是:,即,
故选:B.
5.解:当与重合时,折痕是的角平分线;
当点A与点B重合时,折叠是的中垂线,
故选:C.
6.本题实质上是要确定三角形外接圆的圆心,三角形外接圆的圆心是三边垂直平分线的交点,
故选B.
7.解:连接CD,如图:
∵N是AC的中点,
∴==1,
∴S△ADN=S△CDN,
同理:S△ABN=S△CBN,
设S△ADN=S△CDN=a,
∵△ABC的面积是1,
∴S△ABN=S△CBN=,
∴S△BCD=S△ABD=﹣a,
∵BM=BC,
∴=,
∴==,==,
∴S△CDM=3S△BDM,S△ACM=3S△ABM,
∴S△CDM=S△BCD=×(﹣a)=﹣a,S△ACM=S△ABC=,
∵S△ACM=S四边形CMDN+S△ADN=S△CDM+S△CDN+S△ADN,
即:=﹣a+a+a,
解得:a=,
∴S△ADN=,
故选:B.
8.A. ∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故A正确.
B. 由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故B正确.
C. 在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90° ∠ABD,
故C正确;
D. ∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90° ∠ABC,
∴∠ADB不等于∠CDB,∴D错误;
故选D.
9.解:∵,,
∴,
∵平分,
∴,
∵是的边上的高,
∴,
∵,
∴,
∴,
故选:A.
10.解:∵为外角的平分线,平分,
∴,,
又∵是的外角,
∴,
故正确,
∵,分别平分,
∴,,
∴
,
故错误,
∵平分,平分,
∴,,
∴,
∴是的外角,
∴,
故正确,
综上所述正确的结论是,
故选:.
11.解:延长交于,延长交于,如图,
,
在直角中,;
在中,,
,
,
,
;
故选:C.
12.∵AB∥CD,
∴∠C=∠ABC=30°,
又∵CD=CE,
∴∠D=∠CED,
∵∠C+∠D+∠CED=180°,即30°+2∠D=180°,
∴∠D=75°.
故选B.
13.解: 在Rt△ABC 中,
∵∠B=90°,
∴∠A+∠C=90°,
∵∠DEC=∠A,
∴∠DEC+∠C=90°,
∴∠EDC=90°,
∴△EDC 是直角三角形,
故答案为 直角三角形.
14.取网格点M、N,如图,
结合网格,利用割补法,可得:,
∵,
∴,
∵,,
∴,
∴,
∴,
故答案为:.
15. AD是BC边上的中线
CD= BD
△ADC的周长比△ABD的周长多2cm
(AC+ CD+ AD)-(AD+ DB+ AB)= 2cm
AC - AB = 2cm
AB = 4cm
AC = 6cm
故答案为:6.
16.解:三角形的三条中线的交点叫三角形的重心,
故答案为:重心.
17.解:∵DE∥BC,∠ADE=35°,
∴∠ADE=∠B=35°,
∵∠C=120°,∠A+∠B+∠C=180°,
∴∠A=180°-∠B-∠C=180°-35°-120°=25°.
故答案是:25°.
18.∵,
∴,
由折叠的性质得,,
∵,
∴,
∴,
∴,
故答案为:.
19.解:如图,延长交于点,
,
,
,
,
又,
,
故答案为:105.
20.解;∵平分,平分,
∴,,
∵由三角形外角的性质可得,,
∴,
以此类推,
,
……
∴,
故答案为:.
21.根据图形可得,BE是△ABC中AC边上的高.
故答案为:BE.
22.解:∵,
∴3<第三边<7,
∵第三边为奇数,
∴第三边长为.
故答案为:.
23.解:学校大门做成伸缩门,这是应用了四边形不稳定性的特性.
故答案为:不稳定性.
24.解:分两种情况讨论:
当是锐角三角形时,如图,
于,,
;
当是钝角三角形时,如图,
于,,
;
综上所述,或,
故答案为:或.
25.解:以为公共边的“共边三角形”有与、与、与共3对.
故答案为:3.
26.解:正方形的面积为10×10=100()
∴100÷4÷2=12.5()
∴涂色正方形的面积是12.5.
故答案为:12.5.
27.解:在木门上加钉了一根木条,把一个四边形分成了两个三角形,
这样做的道理是三角形具有稳定性.
故答案为:稳定性.
28.根据三角形的三边关系可知,以其中三条线段为边长,可以组成三角形的是:
2cm、3cm、4cm;3cm、4cm、5cm;2cm、4cm、5cm.
共3个三角形.
故答案为3
29.(1)如下图
(2)如下图
(3)如下图
30.解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上根木条;
要使一个边形木架不变形,至少再钉上根木条.
31.解:H建在、的交点处,理由如下:
连接、相交于点H,任取一点,连接、、、,
在中,,
在中,,
,
,
,
最小,
即维修站H建在、的交点处,才能使它到四口油井的距离之和最小.
32.试题分析:(1)利用平移变换的性质得出对应点位置进而得出答案;
(2)利用平移变换的性质得出答案;
(3)利用网格结合三角形中线的性质得出答案;
(4)利用网格结合三角形高线的性质得出答案;
(5)利用平移的性质结合三角形面积求法得出答案.
解:(1)如图所示:△A′B′C′即为所求;
(2)连接AA′,CC′,则这两条线段之间的关系是平行且相等.
故答案为平行且相等;
(3)如图所示:BD即为所求;
(4)如图所示:CE即为所求;
(5)△A′B′C′的面积为△ABC的面积:×5×4=10.
故答案为10.
33.(1)解:是边上的高,,的面积为24,
,
为边上的中线,
是的中点,
.
(2)解:为边的高,
,.
.
为的角平分线,
,
.
34.(1)解:∵,是边上的高,
∴ ,
∴,
即的长度为;
(2)解:如图,∵是直角三角形,,,,
∴,
又∵是边的中线,
∴,
∴,即,
∴.
∴的面积是;
(3)解:∵是边的中线,
∴,
∴的周长﹣的周长 ,
即和的周长的差是.
35.(1)解:如图,直线即为所作;
;
(2)解:如图,直线即为所作;
(3)解:如图,直线即为所作;
(4)解:如图,线段即为所作.
36.解:∵,
∴ .
∵,
∴.
∵,,
∴.
∵为的角平分线,
∴.
∴.
37.(1)解:如图,△即为所求.
(2)解:△的面积=2.
即△的面积为2.
38.解:∵,
∴,
∵,
∴,
∴,
解得:.
39.∵DE∥BC,
∴∠ADE=∠B=50°;
由题意得:∠FDE=∠ADE=50°,
∴∠BDF=180°-2×50°=80°.
40.解:∵,,
∴,
∴,
∴,
∵是边上的高,
∴,
∴.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
