圆柱的表面积应用题专题突破-数学六年级下册苏教版(含答案)
文档属性
| 名称 | 圆柱的表面积应用题专题突破-数学六年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 335.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 17:52:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
圆柱的表面积应用题专题突破-数学六年级下册苏教版
1.博物馆里有一根圆柱体柱子,高3米,粗15.7分米。要工将这根柱子重新粉刷,粉刷1平方要32元,那么粉刷一根柱子大约需要多少钱?
2.一个圆柱形蓄水池,底面半径是10米,高3米。在池内侧面和池底抹一层水泥,需要抹水泥的面积是多少?
3.用彩绳扎一个圆柱形的蛋糕盒(如图),打结处正好是底面圆心,打结用去25厘米。(单位:cm)
(1)捆扎这个蛋糕盒至少用彩绳多少厘米?
(2)在蛋糕盒的整个侧面贴上彩纸,至少需要彩纸多少平方厘米?
4.两个相同圆柱体的木块底面相拼,拼成一个高12厘米的圆柱体,表面积就减少了100.48平方厘米,求原来每个圆柱体的表面积是多少?
5.压路机的滚筒是圆柱形,前轮直径1.5m,轮宽2m,如果每分钟前轮转动8圈。这台压路机工作1分钟前进了多少米?工作1分钟前轮压过路面积是多少平方米?
6.一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做,做这顶帽子一共用布多少平方厘米?
(单位cm)
7.一个底面周长和高相等的圆柱体,如果高降低1厘米,它的表面积就减少6.28平方厘米,这个圆柱的底面积是多少平方厘米?
8.一个圆柱的表面积和长方形的面积相等,长方形的长等于圆柱的底面周长。已知长方形的面积是251.2平方厘米,圆柱的底面半径是2厘米,求圆柱的高是多少厘米。
9.一种圆柱形的铁皮通风管长4米,横截面的直径是3分米,要做20节这样的通风管,至少需要多少平方分米的铁皮?
10.把一张边长20厘米的正方形纸卷成尽可能大的圆筒。
(1)圆筒的底面周长是多厘米?
(2)高是多少厘米?
(3)侧面的面积是多少平方厘米?
11.一个正方体的木块,其棱长总和是240厘米,在这个正方体里削一个最大的圆柱,这个圆柱的表面积是多少平方厘米?
12.一个圆柱木块的高是4分米,沿底面直径将圆柱分成两个完全一样的半圆柱(如下图),两个半圆柱的表面积和比原来圆柱的表面积增加了48平方分米。每个半圆柱的表面积是多少?
13.一个圆柱的底面周长和高相等,如果高增加4cm,表面积就增加125.6cm2,原来这个圆柱的表面积是多少平方厘米?
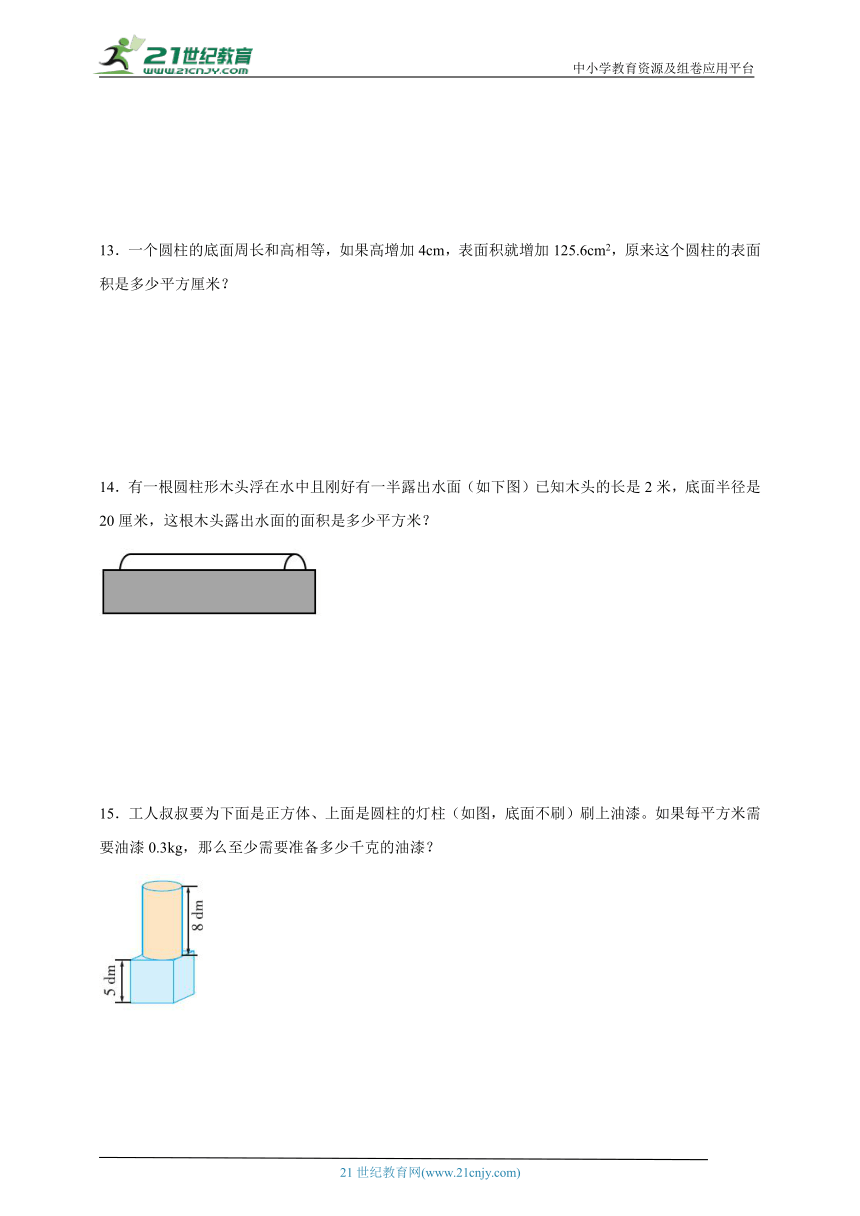
14.有一根圆柱形木头浮在水中且刚好有一半露出水面(如下图)已知木头的长是2米,底面半径是20厘米,这根木头露出水面的面积是多少平方米?
15.工人叔叔要为下面是正方体、上面是圆柱的灯柱(如图,底面不刷)刷上油漆。如果每平方米需要油漆0.3kg,那么至少需要准备多少千克的油漆?
16.下图是一个玩具陀螺,如果想把陀螺的圆柱部分涂上油漆,涂油漆的部分的面积是多少?(单位:厘米)
17.图形的下半部分是棱长10厘米的正方体,上半部分是圆柱的一半.计算这个图形的表面积.
18.一个圆柱,底面直径是50厘米,高是18分米,侧面积是多少平方分米?
19.一个圆柱的侧面积是188.4dm2,底面半径是2dm。它的高是多少?
20.学校走廊有6根圆柱体柱子,每根柱子的底面周长是2.5米,高是4米,要给它们重新漆油漆,按1千克油漆能漆5平方米计算,这6根柱子需要多少千克油漆?
21.一个圆柱体的表面积比侧面积大25.12平方米,这个圆柱体的底面半径是多少?
参考答案:
1.473.26元
【详解】15.7分米=1.57米
1.57×3.14×3×32
=14.7894×32
≈473.26(元)
答:粉刷一根柱子大约需要473.26元。
粉刷的是圆柱的侧面积,侧面积等于底面周长乘高。
2.502.4平方米
【分析】抹水泥的面积就是蓄水池的侧面积加下底的面积,将数据代入此关系式即可求解。
【详解】3.14×10×2×3+3.14×10×10
=188.4+314
=502.4(平方米)
答:需要抹水泥的面积是502.4平方米。
【点睛】此题主要考查圆柱体的表面积的计算方法在实际生活中的应用。
3.(1)285厘米;
(2)2355平方厘米
【分析】(1)看图可知,用的彩绳包含圆柱的4条底面直径,4条高和打结25厘米,据此列式解答即可;
(2)求彩纸面积就是求圆柱侧面积,根据圆柱侧面积=底面周长×高,列式解答即可。
【详解】(1)50×4+15×4+25
=200+60+25
=285(厘米)
答:捆扎这个蛋糕盒至少用彩绳285厘米。
(2)50×3.14×15=2355(平方厘米)
答:至少需要彩纸2355平方厘米。
【点睛】本题考查了圆柱特征和侧面积,圆柱侧面沿高展开是一个长方形,圆柱侧面积公式根据长方形面积的求法推导而来。
4.251.2平方厘米
【分析】本题中,表面积减少的部分就是拼接时相互重合的两个面的面积。所以我们先用100.48÷2÷3.14可得出圆柱体底面半径的平方,再还原成半径;两个圆柱体高12厘米,则一个高为12÷2=6(厘米)。这样,要求的圆柱体的半径、高都已知了,就可以计算其表面积了。尤其注意的是,表面积用侧面积+拼接时减少的面积来计算更简便。
【详解】100.48÷2÷3.14
=50.24÷3.14
=16
16=42,即半径=4厘米,
12÷2=6(厘米),即高=6厘米,
S圆柱=S侧+2×S底
=2×3.14×4×6+100.48
=150.72+100.48
=251.2(平方厘米)
答:原来每个圆柱体的表面积是251.2平方厘米。
【点睛】本题难点在于底面半径的确定,先要求出一个圆柱底面的面积,再将S=πr2变形,得出半径,其次,小数混合运算量也不小,要仔细计算,防止出错。
5.37.68米;75.36平方米
【分析】压路机滚筒前进一圈,前进的距离是底面周长,根据圆的周长公式求出底面周长×8=1分钟前进的距离,压路机压出的路面形状是长方形,长方形的长是前进的距离,宽是滚筒轮宽,根据长方形面积公式计算出压路面积即可。
【详解】3.14×1.5×8=37.68(米)
37.68×2=75.36(平方米)
答:这台压路机工作1分钟前进了37.68米,工作1分钟前轮压过路面积是75.36平方米。
【点睛】本题考查了圆柱侧面积,圆柱侧面积=底面周长×高。
6.1884平方厘米
【分析】利用平移,将圆柱形部分上面的面平移到下面,与红布组成一个大圆,用大圆面积+圆柱形部分的侧面积即可。
【详解】3.14×(20÷2+10)2+3.14×20×10
=3.14×(10+10)2+628
=3.14×202+628
=1256+628
=1884(平方厘米)
答:做这顶帽子一共用布1884平方厘米。
【点睛】本题考查了组合体的表面积,圆柱侧面积=底面周长×高。
7.3.14平方厘米
【分析】因为圆柱体的底面周长和高相等,高降低1厘米,减少的面积就是高为1厘米的圆柱的侧面积。根据减少的面积求出底面周长,再求出底面半径,最后求出圆柱的底面积。
【详解】底面半径:
6.28÷1÷3.14÷2
=6.28÷3.14÷2
=2÷2
=1(厘米)
底面积:3.14×1×1=3.14(平方厘米)
答:圆柱的底面积是3.14平方厘米。
【点睛】本题的关键是圆柱的高降低1厘米,表面积减少的是高为1厘米的圆柱的侧面积,根据条件求出圆柱的底面周长。
8.18厘米
【分析】根据圆柱的底面半径是2厘米,可以求出圆柱的底面积,用长方形的面积减去圆柱的2个底面积,即可得出圆柱的侧面积,据此利用侧面积除以圆柱的底面周长,即可求出圆柱的高。
【详解】251.2-3.14×2×2×2
=251.2-3.14×8
=251.2-25.12
=226.08(平方厘米)
226.08÷(3.14×2×2)
=226.08÷12.56
=18(厘米)
答:圆柱的高是18厘米。
【点睛】解答此题的关键是根据圆柱体的表面积与底面积,明确出这个圆柱体的侧面积,再利用侧面积公式求出圆柱的高即可解答。
9.7536平方分米
【分析】先根据圆柱侧面积=圆柱底面周长×高,求出一根通风管需要的铁皮,再乘20即可解答。
【详解】4米=40分米
3.14×3×40×20
=3.14×2400
=7536(平方分米)
答:至少需要7536平方分米的铁皮。
【点睛】此题考查了圆柱的侧面积公式的计算应用,此类问题要结合生活实际进行解答。
10.(1)20厘米
(2)20厘米
(3)400平方厘米
【分析】根据圆柱体的特征,圆柱体的侧面是一个曲面沿高展开得到的长方形或正方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,正方形的边长等于圆柱的底面周长和高;圆柱的侧面积=底面周长×高,据此求解。
【详解】(1)圆筒的底面周长等于正方形的边长,所以圆筒的底面周长是20厘米。
答:圆筒的底面周长是20厘米。
(2)圆筒的高也是正方形的边长,所以圆筒的高是20厘米。
答:圆筒的高是20厘米。
(3)20×20=400(平方厘米)
答:侧面的面积是400平方厘米。
【点睛】本题考查圆柱展开图的特征以及圆柱的侧面积公式。
11.1884平方厘米
【分析】根据题意,将一个正方体木块削成一个最大的圆柱,正方体的棱长是圆柱的底面直径和高,先用正方体的棱长总和÷12=正方体的棱长,然后用侧面积+2个底面积=圆柱的表面积,据此列式解答。
【详解】正方体的棱长为:240÷12=20(厘米)
所削得最大圆柱的直径为20厘米
圆柱的侧面积是:πdh=3.14×20×20=1256(平方厘米)
圆柱底面圆的面积是:πr2=3.14×(20÷2)2=3.14×100=314(平方厘米)
则该圆柱的表面积是:1256+2×314=1884(平方厘米)
答:这个圆柱的表面积是1884平方厘米。
【点睛】本题考查了正方体的棱长总和及圆柱的表面积。
12.89.94平方分米
【分析】题目只给了两个数据,一个是高4分米,一个是增加的48平方分米,我们可从这48平方分米入手,因为它代表了两个长方形的面积,这两个长方形一模一样,是过圆柱上下底面两条直径及和直径在同一平面内的两条高形成的长方形。这个长方形很特殊,它的宽是底面直径,长是圆柱的高。把48平均分成两份,每份是24平方分米,结合圆柱的高是4分米,能够计算出长方形的宽,也就是圆柱的底面直径。有了圆柱的底面直径再结合圆柱的高,就可以求得每个半圆柱的表面积了。
【详解】48÷2÷4
=24÷4
=6(分米)
48÷2+3.14×(6÷2)2+3.14×6×4÷2
=24+28.26+37.68
=89.94(平方分米)
答:每个半圆柱的表面积是89.94平方分米。
【点睛】切圆柱的方法不止一种,即可以平行于底面切出横截面为圆形,还可以如本题沿底面直径将圆柱分成两个完全一样的半圆柱,有关第二种方法的问题更复杂些。突破点就在于“直径”,利用现有的数据“高”和“纵切面截面(两个长方形)的面积和”先求出直径,问题就迎刃而解了。只是也许思考的路上会走弯路,不能一步到位,这也是正常的,如果能在今后的学习中举一反三,就更好了。
13.1142.96cm2
【分析】圆柱的高增加了4cm,底面面积还是原来的,只是增加部分的圆柱增加了侧面积。把增加部分展开,看作长方形。长方形的面积就是125.6cm2,宽为4cm。关键是求出长方形的长,用面积除以宽可得长。这个长就是圆柱的底面周长,接下来再求出直径、半径,原来圆柱的表面积就求出来了。还要注意圆柱的底面周长和高相等。
【详解】125.6÷4=31.4(cm)
31.4×31.4+3.14×(31.4÷3.14÷2)2×2
=985.96+3.14×50
=985.96+157
=1142.96(cm2)
答:原来这个圆柱的表面积是1142.96平方厘米。
【点睛】这道题较为复杂:①圆柱的底面周长和高相等,计算时要注意数据的选取;②高增加了,就增加了表面积,就要研究增加的部分,从求增加部分的底面周长入手。还要注意计算量很大。
14.1.3816平方米
【分析】这根木头露出水面的面积=圆柱的侧面积÷2+1个圆的面积,圆柱的侧面积=底面周长×高,底面周长=π×2×半径,1米=20厘米,圆的面积=π×半径×半径;依此换算并计算即可。
【详解】20厘米=0.2米
3.14×2×0.2
=6.28×0.2
=1.256(米)
1.256×2÷2=1.256(平方米)
3.14×0.2×0.2
=0.628×0.2
=0.1256(平方米)
1.256+0.1256=1.3816(平方米)
答:这根木头露出水面的面积是1.3816平方米。
【点睛】此题考查的是圆柱表面积的计算,应明确:这根木头露出水面的面积=圆柱的侧面积÷2+1个圆的面积。
15.0.7518kg
【详解】5dm=0.5m 8dm=0.8m
(0.5×0.5×5+3.14×0.5×0.8)×0.3=0.7518(kg)
答:至少需要准备0.7518kg的油漆。
16.122.46平方厘米
【详解】3.14×(6÷2)2+3.14×6×5
=3.14×32+3.14×30
=3.14×9+94.2
=28.6+98.2
=122.46(平方厘米)
答:涂油漆的部分的面积是122.46平方厘米。
17.735.5平方厘米
【详解】10×10×5=500(平方厘米)
×3.14×10×10=157(平方厘米)
3.14×(10÷2)2=78.5(平方厘米)
500+157+78.5=735.5(平方厘米)
18.282.6平方分米
【详解】50厘米=5分米
3.14×5×18
=15.7×18
=282.6(平方分米)
答:侧面积是282.6平方分米。
19.15dm
【分析】圆柱侧面积公式为:S=2πrh,据此求解。
【详解】188.4÷2÷2÷3.14
=47.1÷3.14
=15(分米)
答:它的高是15分米。
【点睛】能够熟练运用圆柱体的侧面积公式去解决问题。
20.12千克
【详解】2.5×4×6÷5=12(千克)
答:这6根柱子需要12千克油漆。
21.2米
【详解】25.12÷2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(米)
答:半径是2米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆柱的表面积应用题专题突破-数学六年级下册苏教版
1.博物馆里有一根圆柱体柱子,高3米,粗15.7分米。要工将这根柱子重新粉刷,粉刷1平方要32元,那么粉刷一根柱子大约需要多少钱?
2.一个圆柱形蓄水池,底面半径是10米,高3米。在池内侧面和池底抹一层水泥,需要抹水泥的面积是多少?
3.用彩绳扎一个圆柱形的蛋糕盒(如图),打结处正好是底面圆心,打结用去25厘米。(单位:cm)
(1)捆扎这个蛋糕盒至少用彩绳多少厘米?
(2)在蛋糕盒的整个侧面贴上彩纸,至少需要彩纸多少平方厘米?
4.两个相同圆柱体的木块底面相拼,拼成一个高12厘米的圆柱体,表面积就减少了100.48平方厘米,求原来每个圆柱体的表面积是多少?
5.压路机的滚筒是圆柱形,前轮直径1.5m,轮宽2m,如果每分钟前轮转动8圈。这台压路机工作1分钟前进了多少米?工作1分钟前轮压过路面积是多少平方米?
6.一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做,做这顶帽子一共用布多少平方厘米?
(单位cm)
7.一个底面周长和高相等的圆柱体,如果高降低1厘米,它的表面积就减少6.28平方厘米,这个圆柱的底面积是多少平方厘米?
8.一个圆柱的表面积和长方形的面积相等,长方形的长等于圆柱的底面周长。已知长方形的面积是251.2平方厘米,圆柱的底面半径是2厘米,求圆柱的高是多少厘米。
9.一种圆柱形的铁皮通风管长4米,横截面的直径是3分米,要做20节这样的通风管,至少需要多少平方分米的铁皮?
10.把一张边长20厘米的正方形纸卷成尽可能大的圆筒。
(1)圆筒的底面周长是多厘米?
(2)高是多少厘米?
(3)侧面的面积是多少平方厘米?
11.一个正方体的木块,其棱长总和是240厘米,在这个正方体里削一个最大的圆柱,这个圆柱的表面积是多少平方厘米?
12.一个圆柱木块的高是4分米,沿底面直径将圆柱分成两个完全一样的半圆柱(如下图),两个半圆柱的表面积和比原来圆柱的表面积增加了48平方分米。每个半圆柱的表面积是多少?
13.一个圆柱的底面周长和高相等,如果高增加4cm,表面积就增加125.6cm2,原来这个圆柱的表面积是多少平方厘米?
14.有一根圆柱形木头浮在水中且刚好有一半露出水面(如下图)已知木头的长是2米,底面半径是20厘米,这根木头露出水面的面积是多少平方米?
15.工人叔叔要为下面是正方体、上面是圆柱的灯柱(如图,底面不刷)刷上油漆。如果每平方米需要油漆0.3kg,那么至少需要准备多少千克的油漆?
16.下图是一个玩具陀螺,如果想把陀螺的圆柱部分涂上油漆,涂油漆的部分的面积是多少?(单位:厘米)
17.图形的下半部分是棱长10厘米的正方体,上半部分是圆柱的一半.计算这个图形的表面积.
18.一个圆柱,底面直径是50厘米,高是18分米,侧面积是多少平方分米?
19.一个圆柱的侧面积是188.4dm2,底面半径是2dm。它的高是多少?
20.学校走廊有6根圆柱体柱子,每根柱子的底面周长是2.5米,高是4米,要给它们重新漆油漆,按1千克油漆能漆5平方米计算,这6根柱子需要多少千克油漆?
21.一个圆柱体的表面积比侧面积大25.12平方米,这个圆柱体的底面半径是多少?
参考答案:
1.473.26元
【详解】15.7分米=1.57米
1.57×3.14×3×32
=14.7894×32
≈473.26(元)
答:粉刷一根柱子大约需要473.26元。
粉刷的是圆柱的侧面积,侧面积等于底面周长乘高。
2.502.4平方米
【分析】抹水泥的面积就是蓄水池的侧面积加下底的面积,将数据代入此关系式即可求解。
【详解】3.14×10×2×3+3.14×10×10
=188.4+314
=502.4(平方米)
答:需要抹水泥的面积是502.4平方米。
【点睛】此题主要考查圆柱体的表面积的计算方法在实际生活中的应用。
3.(1)285厘米;
(2)2355平方厘米
【分析】(1)看图可知,用的彩绳包含圆柱的4条底面直径,4条高和打结25厘米,据此列式解答即可;
(2)求彩纸面积就是求圆柱侧面积,根据圆柱侧面积=底面周长×高,列式解答即可。
【详解】(1)50×4+15×4+25
=200+60+25
=285(厘米)
答:捆扎这个蛋糕盒至少用彩绳285厘米。
(2)50×3.14×15=2355(平方厘米)
答:至少需要彩纸2355平方厘米。
【点睛】本题考查了圆柱特征和侧面积,圆柱侧面沿高展开是一个长方形,圆柱侧面积公式根据长方形面积的求法推导而来。
4.251.2平方厘米
【分析】本题中,表面积减少的部分就是拼接时相互重合的两个面的面积。所以我们先用100.48÷2÷3.14可得出圆柱体底面半径的平方,再还原成半径;两个圆柱体高12厘米,则一个高为12÷2=6(厘米)。这样,要求的圆柱体的半径、高都已知了,就可以计算其表面积了。尤其注意的是,表面积用侧面积+拼接时减少的面积来计算更简便。
【详解】100.48÷2÷3.14
=50.24÷3.14
=16
16=42,即半径=4厘米,
12÷2=6(厘米),即高=6厘米,
S圆柱=S侧+2×S底
=2×3.14×4×6+100.48
=150.72+100.48
=251.2(平方厘米)
答:原来每个圆柱体的表面积是251.2平方厘米。
【点睛】本题难点在于底面半径的确定,先要求出一个圆柱底面的面积,再将S=πr2变形,得出半径,其次,小数混合运算量也不小,要仔细计算,防止出错。
5.37.68米;75.36平方米
【分析】压路机滚筒前进一圈,前进的距离是底面周长,根据圆的周长公式求出底面周长×8=1分钟前进的距离,压路机压出的路面形状是长方形,长方形的长是前进的距离,宽是滚筒轮宽,根据长方形面积公式计算出压路面积即可。
【详解】3.14×1.5×8=37.68(米)
37.68×2=75.36(平方米)
答:这台压路机工作1分钟前进了37.68米,工作1分钟前轮压过路面积是75.36平方米。
【点睛】本题考查了圆柱侧面积,圆柱侧面积=底面周长×高。
6.1884平方厘米
【分析】利用平移,将圆柱形部分上面的面平移到下面,与红布组成一个大圆,用大圆面积+圆柱形部分的侧面积即可。
【详解】3.14×(20÷2+10)2+3.14×20×10
=3.14×(10+10)2+628
=3.14×202+628
=1256+628
=1884(平方厘米)
答:做这顶帽子一共用布1884平方厘米。
【点睛】本题考查了组合体的表面积,圆柱侧面积=底面周长×高。
7.3.14平方厘米
【分析】因为圆柱体的底面周长和高相等,高降低1厘米,减少的面积就是高为1厘米的圆柱的侧面积。根据减少的面积求出底面周长,再求出底面半径,最后求出圆柱的底面积。
【详解】底面半径:
6.28÷1÷3.14÷2
=6.28÷3.14÷2
=2÷2
=1(厘米)
底面积:3.14×1×1=3.14(平方厘米)
答:圆柱的底面积是3.14平方厘米。
【点睛】本题的关键是圆柱的高降低1厘米,表面积减少的是高为1厘米的圆柱的侧面积,根据条件求出圆柱的底面周长。
8.18厘米
【分析】根据圆柱的底面半径是2厘米,可以求出圆柱的底面积,用长方形的面积减去圆柱的2个底面积,即可得出圆柱的侧面积,据此利用侧面积除以圆柱的底面周长,即可求出圆柱的高。
【详解】251.2-3.14×2×2×2
=251.2-3.14×8
=251.2-25.12
=226.08(平方厘米)
226.08÷(3.14×2×2)
=226.08÷12.56
=18(厘米)
答:圆柱的高是18厘米。
【点睛】解答此题的关键是根据圆柱体的表面积与底面积,明确出这个圆柱体的侧面积,再利用侧面积公式求出圆柱的高即可解答。
9.7536平方分米
【分析】先根据圆柱侧面积=圆柱底面周长×高,求出一根通风管需要的铁皮,再乘20即可解答。
【详解】4米=40分米
3.14×3×40×20
=3.14×2400
=7536(平方分米)
答:至少需要7536平方分米的铁皮。
【点睛】此题考查了圆柱的侧面积公式的计算应用,此类问题要结合生活实际进行解答。
10.(1)20厘米
(2)20厘米
(3)400平方厘米
【分析】根据圆柱体的特征,圆柱体的侧面是一个曲面沿高展开得到的长方形或正方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,正方形的边长等于圆柱的底面周长和高;圆柱的侧面积=底面周长×高,据此求解。
【详解】(1)圆筒的底面周长等于正方形的边长,所以圆筒的底面周长是20厘米。
答:圆筒的底面周长是20厘米。
(2)圆筒的高也是正方形的边长,所以圆筒的高是20厘米。
答:圆筒的高是20厘米。
(3)20×20=400(平方厘米)
答:侧面的面积是400平方厘米。
【点睛】本题考查圆柱展开图的特征以及圆柱的侧面积公式。
11.1884平方厘米
【分析】根据题意,将一个正方体木块削成一个最大的圆柱,正方体的棱长是圆柱的底面直径和高,先用正方体的棱长总和÷12=正方体的棱长,然后用侧面积+2个底面积=圆柱的表面积,据此列式解答。
【详解】正方体的棱长为:240÷12=20(厘米)
所削得最大圆柱的直径为20厘米
圆柱的侧面积是:πdh=3.14×20×20=1256(平方厘米)
圆柱底面圆的面积是:πr2=3.14×(20÷2)2=3.14×100=314(平方厘米)
则该圆柱的表面积是:1256+2×314=1884(平方厘米)
答:这个圆柱的表面积是1884平方厘米。
【点睛】本题考查了正方体的棱长总和及圆柱的表面积。
12.89.94平方分米
【分析】题目只给了两个数据,一个是高4分米,一个是增加的48平方分米,我们可从这48平方分米入手,因为它代表了两个长方形的面积,这两个长方形一模一样,是过圆柱上下底面两条直径及和直径在同一平面内的两条高形成的长方形。这个长方形很特殊,它的宽是底面直径,长是圆柱的高。把48平均分成两份,每份是24平方分米,结合圆柱的高是4分米,能够计算出长方形的宽,也就是圆柱的底面直径。有了圆柱的底面直径再结合圆柱的高,就可以求得每个半圆柱的表面积了。
【详解】48÷2÷4
=24÷4
=6(分米)
48÷2+3.14×(6÷2)2+3.14×6×4÷2
=24+28.26+37.68
=89.94(平方分米)
答:每个半圆柱的表面积是89.94平方分米。
【点睛】切圆柱的方法不止一种,即可以平行于底面切出横截面为圆形,还可以如本题沿底面直径将圆柱分成两个完全一样的半圆柱,有关第二种方法的问题更复杂些。突破点就在于“直径”,利用现有的数据“高”和“纵切面截面(两个长方形)的面积和”先求出直径,问题就迎刃而解了。只是也许思考的路上会走弯路,不能一步到位,这也是正常的,如果能在今后的学习中举一反三,就更好了。
13.1142.96cm2
【分析】圆柱的高增加了4cm,底面面积还是原来的,只是增加部分的圆柱增加了侧面积。把增加部分展开,看作长方形。长方形的面积就是125.6cm2,宽为4cm。关键是求出长方形的长,用面积除以宽可得长。这个长就是圆柱的底面周长,接下来再求出直径、半径,原来圆柱的表面积就求出来了。还要注意圆柱的底面周长和高相等。
【详解】125.6÷4=31.4(cm)
31.4×31.4+3.14×(31.4÷3.14÷2)2×2
=985.96+3.14×50
=985.96+157
=1142.96(cm2)
答:原来这个圆柱的表面积是1142.96平方厘米。
【点睛】这道题较为复杂:①圆柱的底面周长和高相等,计算时要注意数据的选取;②高增加了,就增加了表面积,就要研究增加的部分,从求增加部分的底面周长入手。还要注意计算量很大。
14.1.3816平方米
【分析】这根木头露出水面的面积=圆柱的侧面积÷2+1个圆的面积,圆柱的侧面积=底面周长×高,底面周长=π×2×半径,1米=20厘米,圆的面积=π×半径×半径;依此换算并计算即可。
【详解】20厘米=0.2米
3.14×2×0.2
=6.28×0.2
=1.256(米)
1.256×2÷2=1.256(平方米)
3.14×0.2×0.2
=0.628×0.2
=0.1256(平方米)
1.256+0.1256=1.3816(平方米)
答:这根木头露出水面的面积是1.3816平方米。
【点睛】此题考查的是圆柱表面积的计算,应明确:这根木头露出水面的面积=圆柱的侧面积÷2+1个圆的面积。
15.0.7518kg
【详解】5dm=0.5m 8dm=0.8m
(0.5×0.5×5+3.14×0.5×0.8)×0.3=0.7518(kg)
答:至少需要准备0.7518kg的油漆。
16.122.46平方厘米
【详解】3.14×(6÷2)2+3.14×6×5
=3.14×32+3.14×30
=3.14×9+94.2
=28.6+98.2
=122.46(平方厘米)
答:涂油漆的部分的面积是122.46平方厘米。
17.735.5平方厘米
【详解】10×10×5=500(平方厘米)
×3.14×10×10=157(平方厘米)
3.14×(10÷2)2=78.5(平方厘米)
500+157+78.5=735.5(平方厘米)
18.282.6平方分米
【详解】50厘米=5分米
3.14×5×18
=15.7×18
=282.6(平方分米)
答:侧面积是282.6平方分米。
19.15dm
【分析】圆柱侧面积公式为:S=2πrh,据此求解。
【详解】188.4÷2÷2÷3.14
=47.1÷3.14
=15(分米)
答:它的高是15分米。
【点睛】能够熟练运用圆柱体的侧面积公式去解决问题。
20.12千克
【详解】2.5×4×6÷5=12(千克)
答:这6根柱子需要12千克油漆。
21.2米
【详解】25.12÷2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(米)
答:半径是2米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
