鲁教版七年级数学下册第10章10.2等腰三角形测试题(含答案)
文档属性
| 名称 | 鲁教版七年级数学下册第10章10.2等腰三角形测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 78.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-12 07:44:11 | ||
图片预览

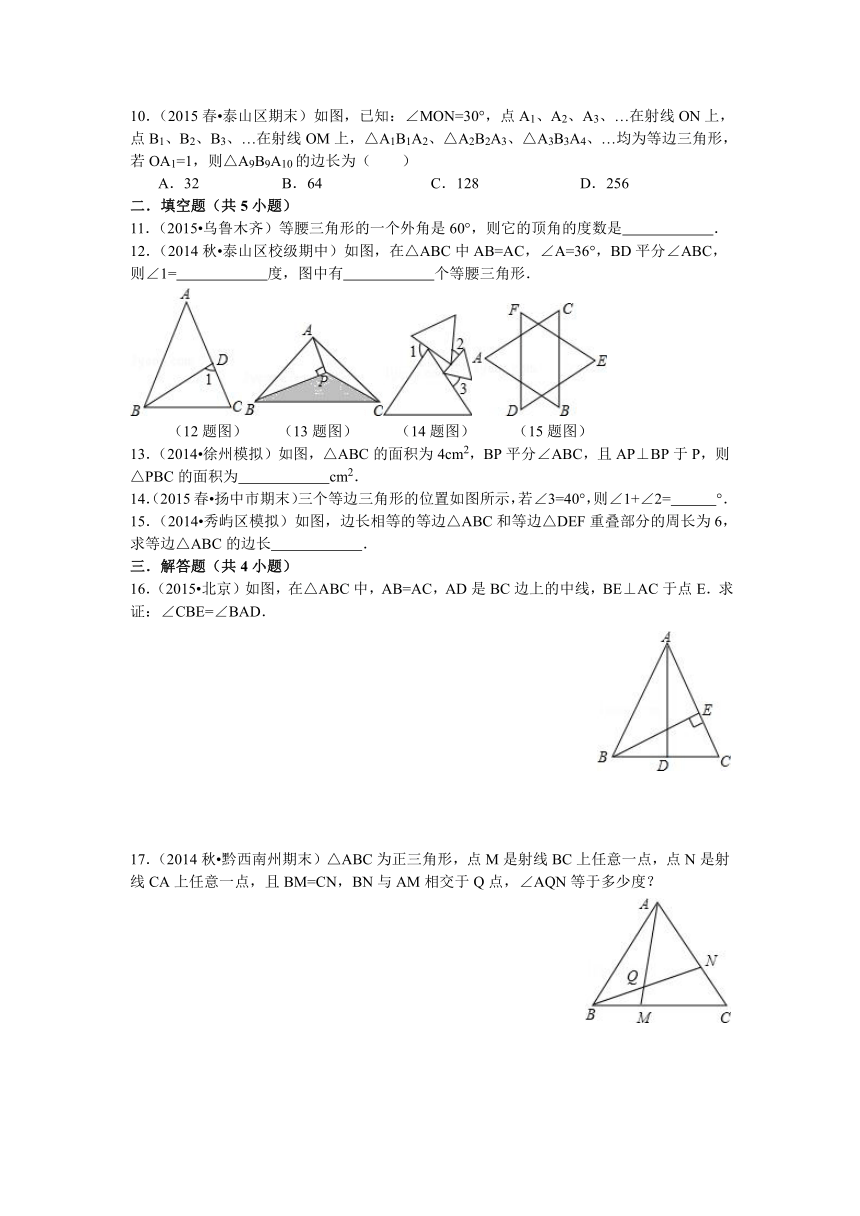
文档简介
鲁教版七年级数学下册第10章10.2等腰三角形测试题(含答案)
一.选择题(共10小题)
1.(2015 盐城)若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A.12 B. 9 C. 12或9 D. 9或7
2.(2015 南宁)如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B. 40° C. 45° D. 50°
(2题图) (3题图) (4题图) (6题图)
3.(2015 黄石)如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
A.36° B. 54° C. 18° D. 64°
4.(2015 淄博模拟)如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )
A.5个 B. 4个 C. 3个 D. 2个
5.(2015 沂源县校级模拟)有3cm,3cm,6cm,6cm,12cm,12cm的六条线段,任选其中的三条线段组成一个等腰三角形,则最多能组成等腰三角形的个数为( )
A.1 B. 2 C. 3 D. 4
6.(2015 威海模拟)如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB、AC于E、F,AB=5,AC=7,BC=8,△AEF的周长为( )
A.13 B. 12 C. 15 D. 20
7.(2015春 泰山区期末)如图,AB=AC,BE平分∠ABC,DE∥BC,图中等腰三角形共有( )
A.1个 B. 2个 C. 3个 D. 4个
(7题图) (10题图)
8.(2015春 青羊区校级月考)在下列结论中:
(1)有一个外角是120°的等腰三角形是等边三角形;
(2)有两个外角相等的等腰三角形是等边三角形;
(3)有一边上的高也是这边上的中线的等腰三角形是等边三角形;
(4)三个外角都相等的三角形是等边三角形.其中正确的个数是( )
A.4个 B. 3个 C. 2个 D. 1个
9.(2015春 定州市期中)等边三角形的边长为2,则该三角形的面积为( )
A. 4 B. C. 2 D. 3
10.(2015春 泰山区期末)如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )
A.32 B. 64 C. 128 D. 256
二.填空题(共5小题)
11.(2015 乌鲁木齐)等腰三角形的一个外角是60°,则它的顶角的度数是 .
12.(2014秋 泰山区校级期中)如图,在△ABC中AB=AC,∠A=36°,BD平分∠ABC,则∠1= 度,图中有 个等腰三角形.
(12题图) (13题图) (14题图) (15题图)
13.(2014 徐州模拟)如图,△ABC的面积为4cm2,BP平分∠ABC,且AP⊥BP于P,则△PBC的面积为 cm2.
14.(2015春 扬中市期末)三个等边三角形的位置如图所示,若∠3=40°,则∠1+∠2= °.
15.(2014 秀屿区模拟)如图,边长相等的等边△ABC和等边△DEF重叠部分的周长为6,求等边△ABC的边长 .
三.解答题(共4小题)
16.(2015 北京)如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
17.(2014秋 黔西南州期末)△ABC为正三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,BN与AM相交于Q点,∠AQN等于多少度?
18.(2014春 博兴县校级期中)等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
19.(2014秋 滨州期末)如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.
鲁教版七年级数学下册第10章10.2等腰三角形测试题参考答案
一.选择题(共10小题)
1.A.2.A.3.B.4.A.5.C.6.B.7.C.8.D.9.B.10.D.
二.填空题(共5小题)
11. 120° .12. 72 3 13. 2 14. 140 °.15. 3 .
三.解答题(共4小题)
16.证明:∵AB=AC,AD是BC边上的中线,BE⊥AC,
∴∠CBE+∠C=∠CAD+∠C=90°,∠CAD=∠BAD,
∴∠CBE=∠BAD.17.
解:证法一.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中,△AMB≌△BNC(SAS),
∵∠ANB=∠C+∠NBC=60°+∠NBC,
∠MAN=∠BAC﹣∠MAB=60°﹣∠MAB,
又∵∠NBC=∠MAB(全等三角形对应角相等),
∴∠ANB+∠MAN=120°,
又∵∠ANQ+∠MAN+∠AQN=180°,
∴∠AQN=180°﹣∠ANB﹣∠MAN,
∠AQN=180°﹣(∠ANB+∠MAN),
=180°﹣120°=60°,
∠BOM=∠AQN=60°(全等三角形对应角相等).
证法二.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中∴△AMB≌△BNC(SAS)
∵∠ANB=∠C+∠NBC=60°+∠NBC
∠MAN=∠BAC﹣∠MAB
又∵∠NBC=∠MAB(全等三角形对应角相等)
∴∠ANB+∠MAN=120°
又∵∠ANQ+∠MAN+∠AQN=180°
∴∠AQN=180°﹣∠ANB﹣∠MAB
∠AQN=180°﹣(∠ANB+∠MAN)
=180°﹣120°=60°
18.解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,∵,∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
19.解:(1)△ODE是等边三角形,
其理由是:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,(2分)
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°(3分)
∴△ODE是等边三角形;(4分)
(2)答:BD=DE=EC,
其理由是:∵OB平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°,(6分)
∵OD∥AB,
∴∠BOD=∠ABO=30°,
∴∠DBO=∠DOB,
∴DB=DO,(7分)
同理,EC=EO,
∵DE=OD=OE,
∴BD=DE=EC.(8分)
一.选择题(共10小题)
1.(2015 盐城)若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A.12 B. 9 C. 12或9 D. 9或7
2.(2015 南宁)如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B. 40° C. 45° D. 50°
(2题图) (3题图) (4题图) (6题图)
3.(2015 黄石)如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
A.36° B. 54° C. 18° D. 64°
4.(2015 淄博模拟)如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )
A.5个 B. 4个 C. 3个 D. 2个
5.(2015 沂源县校级模拟)有3cm,3cm,6cm,6cm,12cm,12cm的六条线段,任选其中的三条线段组成一个等腰三角形,则最多能组成等腰三角形的个数为( )
A.1 B. 2 C. 3 D. 4
6.(2015 威海模拟)如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB、AC于E、F,AB=5,AC=7,BC=8,△AEF的周长为( )
A.13 B. 12 C. 15 D. 20
7.(2015春 泰山区期末)如图,AB=AC,BE平分∠ABC,DE∥BC,图中等腰三角形共有( )
A.1个 B. 2个 C. 3个 D. 4个
(7题图) (10题图)
8.(2015春 青羊区校级月考)在下列结论中:
(1)有一个外角是120°的等腰三角形是等边三角形;
(2)有两个外角相等的等腰三角形是等边三角形;
(3)有一边上的高也是这边上的中线的等腰三角形是等边三角形;
(4)三个外角都相等的三角形是等边三角形.其中正确的个数是( )
A.4个 B. 3个 C. 2个 D. 1个
9.(2015春 定州市期中)等边三角形的边长为2,则该三角形的面积为( )
A. 4 B. C. 2 D. 3
10.(2015春 泰山区期末)如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )
A.32 B. 64 C. 128 D. 256
二.填空题(共5小题)
11.(2015 乌鲁木齐)等腰三角形的一个外角是60°,则它的顶角的度数是 .
12.(2014秋 泰山区校级期中)如图,在△ABC中AB=AC,∠A=36°,BD平分∠ABC,则∠1= 度,图中有 个等腰三角形.
(12题图) (13题图) (14题图) (15题图)
13.(2014 徐州模拟)如图,△ABC的面积为4cm2,BP平分∠ABC,且AP⊥BP于P,则△PBC的面积为 cm2.
14.(2015春 扬中市期末)三个等边三角形的位置如图所示,若∠3=40°,则∠1+∠2= °.
15.(2014 秀屿区模拟)如图,边长相等的等边△ABC和等边△DEF重叠部分的周长为6,求等边△ABC的边长 .
三.解答题(共4小题)
16.(2015 北京)如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
17.(2014秋 黔西南州期末)△ABC为正三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,BN与AM相交于Q点,∠AQN等于多少度?
18.(2014春 博兴县校级期中)等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
19.(2014秋 滨州期末)如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.
鲁教版七年级数学下册第10章10.2等腰三角形测试题参考答案
一.选择题(共10小题)
1.A.2.A.3.B.4.A.5.C.6.B.7.C.8.D.9.B.10.D.
二.填空题(共5小题)
11. 120° .12. 72 3 13. 2 14. 140 °.15. 3 .
三.解答题(共4小题)
16.证明:∵AB=AC,AD是BC边上的中线,BE⊥AC,
∴∠CBE+∠C=∠CAD+∠C=90°,∠CAD=∠BAD,
∴∠CBE=∠BAD.17.
解:证法一.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中,△AMB≌△BNC(SAS),
∵∠ANB=∠C+∠NBC=60°+∠NBC,
∠MAN=∠BAC﹣∠MAB=60°﹣∠MAB,
又∵∠NBC=∠MAB(全等三角形对应角相等),
∴∠ANB+∠MAN=120°,
又∵∠ANQ+∠MAN+∠AQN=180°,
∴∠AQN=180°﹣∠ANB﹣∠MAN,
∠AQN=180°﹣(∠ANB+∠MAN),
=180°﹣120°=60°,
∠BOM=∠AQN=60°(全等三角形对应角相等).
证法二.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中∴△AMB≌△BNC(SAS)
∵∠ANB=∠C+∠NBC=60°+∠NBC
∠MAN=∠BAC﹣∠MAB
又∵∠NBC=∠MAB(全等三角形对应角相等)
∴∠ANB+∠MAN=120°
又∵∠ANQ+∠MAN+∠AQN=180°
∴∠AQN=180°﹣∠ANB﹣∠MAB
∠AQN=180°﹣(∠ANB+∠MAN)
=180°﹣120°=60°
18.解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,∵,∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
19.解:(1)△ODE是等边三角形,
其理由是:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,(2分)
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°(3分)
∴△ODE是等边三角形;(4分)
(2)答:BD=DE=EC,
其理由是:∵OB平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°,(6分)
∵OD∥AB,
∴∠BOD=∠ABO=30°,
∴∠DBO=∠DOB,
∴DB=DO,(7分)
同理,EC=EO,
∵DE=OD=OE,
∴BD=DE=EC.(8分)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
