八年级数学下册人教版第十七章 17.1 勾股定理 同步练习(含答案)
文档属性
| 名称 | 八年级数学下册人教版第十七章 17.1 勾股定理 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 244.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 14:24:10 | ||
图片预览



文档简介
17.1 勾股定理
(同步练习)
一、单选题
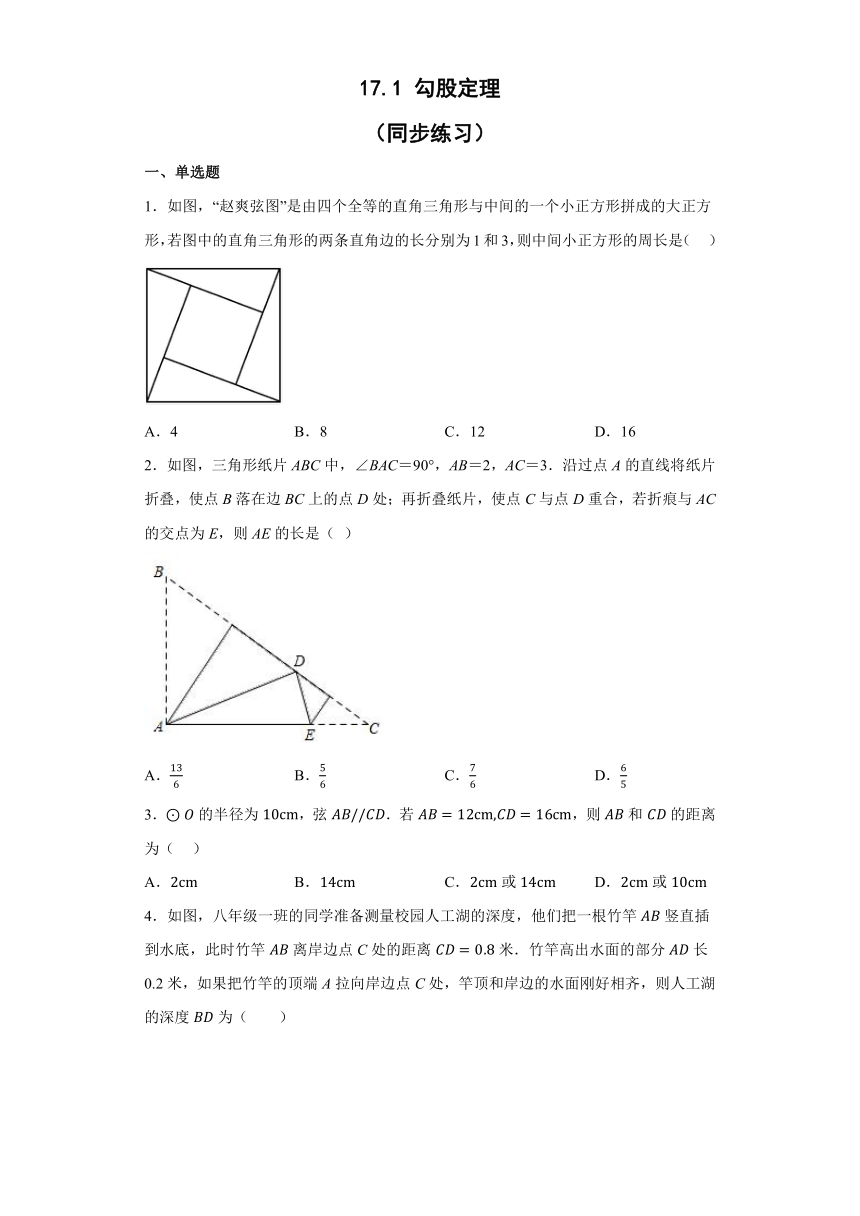
1.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )
A.4 B.8 C.12 D.16
2.如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A. B. C. D.
3.的半径为,弦.若,则和的距离为( )
A. B. C.或 D.或
4.如图,八年级一班的同学准备测量校园人工湖的深度,他们把一根竹竿竖直插到水底,此时竹竿离岸边点C处的距离米.竹竿高出水面的部分长0.2米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则人工湖的深度为( )
A.1.5米 B.1.7米 C.1.8米 D.0.6米
5.已知点M的坐标为,则下列说法正确的是( )
A.点M在第二象限内 B.点M到x轴的距离为3
C.点M关于y轴对称的点的坐标为 D.点M到原点的距离为5
6.已知,斜坡的坡度i=1:2,小明沿斜坡的坡面走了100米,则小明上升的距离是( )
A.米 B.20米 C.米 D.米
7.如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A.20 B.24 C.25 D.26
8.为预防新冠疫情,民生大院入口的正上方 A 处装有红外线激光测温仪(如图所示),测温仪离地面的距离 AB=2.4 米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为 1.8 米的市民 CD 正对门缓慢走到离门 0.8 米的地方时(即 BC=0.8 米),测温仪自动显示体温,则人头顶离测温仪的距离 AD 等于( )
A.1.0 米 B.1.2 米 C.1.25 米 D.1.5 米
9.学校旗杆上的绳子垂到地面还多2米,将绳子的下端拉开6米后,下端刚好接触地面,则旗杆的高度为( )
A.8米 B.10米 C.12米 D.14米
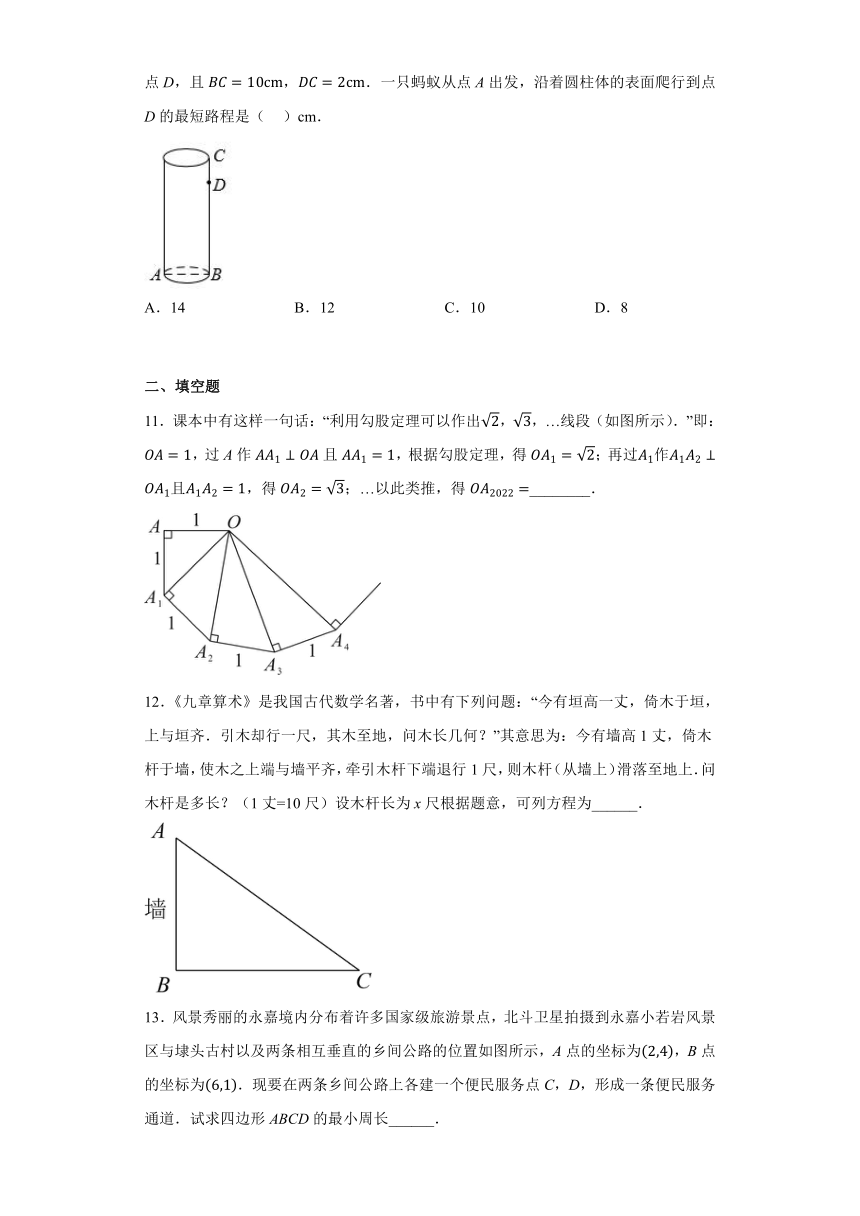
10.如图,圆柱的底面周长为12cm,AB是底面圆的直径,在圆柱表面的高BC上有一点D,且,.一只蚂蚁从点A出发,沿着圆柱体的表面爬行到点D的最短路程是( )cm.
A.14 B.12 C.10 D.8
二、填空题
11.课本中有这样一句话:“利用勾股定理可以作出,,…线段(如图所示).”即:,过A作且,根据勾股定理,得;再过作且,得;…以此类推,得________.
12.《九章算术》是我国古代数学名著,书中有下列问题:“今有垣高一丈,倚木于垣,上与垣齐.引木却行一尺,其木至地,问木长几何?”其意思为:今有墙高1丈,倚木杆于墙,使木之上端与墙平齐,牵引木杆下端退行1尺,则木杆(从墙上)滑落至地上.问木杆是多长?(1丈=10尺)设木杆长为x尺根据题意,可列方程为______.
13.风景秀丽的永嘉境内分布着许多国家级旅游景点,北斗卫星拍摄到永嘉小若岩风景区与埭头古村以及两条相互垂直的乡间公路的位置如图所示,A点的坐标为,B点的坐标为.现要在两条乡间公路上各建一个便民服务点C,D,形成一条便民服务通道.试求四边形ABCD的最小周长______.
14.如图,在△ABC中,AB=AC,BD⊥AC于点D,把线段AC绕点C旋转得到线段CE,点E恰好落在AB的延长线上,,△BCD的面积是8,则BC的长为________.
15.如图,等腰是由三块面向内的镜面组成的,其中,边上靠近点的三等分点处发出一道光线,经镜面两次反射后恰好回到点,若,则光线走过的路径是______.
三、解答题
16.勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法,证法如下:
把两个全等的直角三角形(Rt△ABC≌Rt△DAE)如图1放置,∠DAB=∠B=90°,AC⊥DE于点F,点E在边AB上,现设Rt△ACB两直角边长分别为CB=b、BA=a,斜边长为AC=c,请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理
(1)请根据上述图形的面积关系证明勾股定理;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,CD为两个村庄(看作直线上的两点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为多少千米.
17.如图,有一架秋千,当他静止时,踏板离地的垂直高度,将他往前推送(水平距离)时,秋千的踏板离地的垂直高度,秋千的绳索始终拉得很直,求绳索的长度.
18.如图,由△ABC中,,,.按如图所示方式折叠,使点B、C重合,折痕为DE,求出AE和AD的长.
19.如图所示,在甲村至乙村的公路旁有一块山地正在开发,现需要在处进行爆破,已知点与公路上的停靠站的距离为300米,与公路上的另一停靠站的距离为400米,且.为了安全起见,爆破点周围半径250米范围内不得进入,在进行爆破时,公路是否有危险而需要封锁?如果需要,请计算需要封锁的路段长度;如果不需要,请说明理由.
20.【阅读思考】已知0<x<1,求的最小值
分析:如图,我们可以构造边长为1的正方形ABCD,P为BC边上的动点.设BP=x,则PC=1-x,那么可以用含x的式子表示AP、DP,问题可以转化为AP与PD的和的最小值,用几何知识可以解答
(1)AP+PD的最小值为________
(2)运用以上方法求:的最小值,其中x、y为两正数,且x+y=6
(3)借助上述的思考过程,求的最大值
21.在中,,于点D,于点E,连接.
(1)如图1,当为锐角三角形时,
①依题意补全图形,猜想与之间的数量关系并证明;
②用等式表示线段,,的数量关系,并证明.
(2)如图2,当为钝角时,直接写出线段,,的数量关系.
参考答案:
1.B2.A3.C4.A5.D6.A7.D8.A9.A10.C
11.
12.102+(x-1)2=x2
13.5+
14.
15.
16.(1)解:∵S梯形ABCD=a(a+b),S△EBC=b(a-b),S四边形AECD=c2,
它们满足的关系式为:a(a+b)=b(a-b)+c2,
即a2+b2=c2;
(2)解:如图2①,连接CD,作CE⊥AD于点E,
∵AD⊥AB,BC⊥AB,
∴BC=AE,CE=AB,
∴DE=AD-AE=25-16=9千米,
∴CD= =41(千米),
∴两个村庄相距41千米.
17.
18. ;
19.公路有危险需要封锁,需要封锁的路段长度为140米
20.(1);
(2);
(3).
21.(1)解:①依题意,补全图形,如图1所示.
猜想:,
理由如下:
∵,,
∴,,
∴,
②证明:如图2,在上截取,
连接
∵,,
∴是等腰直角三角形,
∴,
在和中,
∴,
∴,,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴.
(2)解:依题意补全图形,如图3所示,
在上截取,连接,
∵,,
∴,
∴,,,
∴,
∵,
∴,
∴,
在和中,
∴,
∴,,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
∴线段,,的数量关系:.
(同步练习)
一、单选题
1.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )
A.4 B.8 C.12 D.16
2.如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A. B. C. D.
3.的半径为,弦.若,则和的距离为( )
A. B. C.或 D.或
4.如图,八年级一班的同学准备测量校园人工湖的深度,他们把一根竹竿竖直插到水底,此时竹竿离岸边点C处的距离米.竹竿高出水面的部分长0.2米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则人工湖的深度为( )
A.1.5米 B.1.7米 C.1.8米 D.0.6米
5.已知点M的坐标为,则下列说法正确的是( )
A.点M在第二象限内 B.点M到x轴的距离为3
C.点M关于y轴对称的点的坐标为 D.点M到原点的距离为5
6.已知,斜坡的坡度i=1:2,小明沿斜坡的坡面走了100米,则小明上升的距离是( )
A.米 B.20米 C.米 D.米
7.如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A.20 B.24 C.25 D.26
8.为预防新冠疫情,民生大院入口的正上方 A 处装有红外线激光测温仪(如图所示),测温仪离地面的距离 AB=2.4 米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为 1.8 米的市民 CD 正对门缓慢走到离门 0.8 米的地方时(即 BC=0.8 米),测温仪自动显示体温,则人头顶离测温仪的距离 AD 等于( )
A.1.0 米 B.1.2 米 C.1.25 米 D.1.5 米
9.学校旗杆上的绳子垂到地面还多2米,将绳子的下端拉开6米后,下端刚好接触地面,则旗杆的高度为( )
A.8米 B.10米 C.12米 D.14米
10.如图,圆柱的底面周长为12cm,AB是底面圆的直径,在圆柱表面的高BC上有一点D,且,.一只蚂蚁从点A出发,沿着圆柱体的表面爬行到点D的最短路程是( )cm.
A.14 B.12 C.10 D.8
二、填空题
11.课本中有这样一句话:“利用勾股定理可以作出,,…线段(如图所示).”即:,过A作且,根据勾股定理,得;再过作且,得;…以此类推,得________.
12.《九章算术》是我国古代数学名著,书中有下列问题:“今有垣高一丈,倚木于垣,上与垣齐.引木却行一尺,其木至地,问木长几何?”其意思为:今有墙高1丈,倚木杆于墙,使木之上端与墙平齐,牵引木杆下端退行1尺,则木杆(从墙上)滑落至地上.问木杆是多长?(1丈=10尺)设木杆长为x尺根据题意,可列方程为______.
13.风景秀丽的永嘉境内分布着许多国家级旅游景点,北斗卫星拍摄到永嘉小若岩风景区与埭头古村以及两条相互垂直的乡间公路的位置如图所示,A点的坐标为,B点的坐标为.现要在两条乡间公路上各建一个便民服务点C,D,形成一条便民服务通道.试求四边形ABCD的最小周长______.
14.如图,在△ABC中,AB=AC,BD⊥AC于点D,把线段AC绕点C旋转得到线段CE,点E恰好落在AB的延长线上,,△BCD的面积是8,则BC的长为________.
15.如图,等腰是由三块面向内的镜面组成的,其中,边上靠近点的三等分点处发出一道光线,经镜面两次反射后恰好回到点,若,则光线走过的路径是______.
三、解答题
16.勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法,证法如下:
把两个全等的直角三角形(Rt△ABC≌Rt△DAE)如图1放置,∠DAB=∠B=90°,AC⊥DE于点F,点E在边AB上,现设Rt△ACB两直角边长分别为CB=b、BA=a,斜边长为AC=c,请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理
(1)请根据上述图形的面积关系证明勾股定理;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,CD为两个村庄(看作直线上的两点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为多少千米.
17.如图,有一架秋千,当他静止时,踏板离地的垂直高度,将他往前推送(水平距离)时,秋千的踏板离地的垂直高度,秋千的绳索始终拉得很直,求绳索的长度.
18.如图,由△ABC中,,,.按如图所示方式折叠,使点B、C重合,折痕为DE,求出AE和AD的长.
19.如图所示,在甲村至乙村的公路旁有一块山地正在开发,现需要在处进行爆破,已知点与公路上的停靠站的距离为300米,与公路上的另一停靠站的距离为400米,且.为了安全起见,爆破点周围半径250米范围内不得进入,在进行爆破时,公路是否有危险而需要封锁?如果需要,请计算需要封锁的路段长度;如果不需要,请说明理由.
20.【阅读思考】已知0<x<1,求的最小值
分析:如图,我们可以构造边长为1的正方形ABCD,P为BC边上的动点.设BP=x,则PC=1-x,那么可以用含x的式子表示AP、DP,问题可以转化为AP与PD的和的最小值,用几何知识可以解答
(1)AP+PD的最小值为________
(2)运用以上方法求:的最小值,其中x、y为两正数,且x+y=6
(3)借助上述的思考过程,求的最大值
21.在中,,于点D,于点E,连接.
(1)如图1,当为锐角三角形时,
①依题意补全图形,猜想与之间的数量关系并证明;
②用等式表示线段,,的数量关系,并证明.
(2)如图2,当为钝角时,直接写出线段,,的数量关系.
参考答案:
1.B2.A3.C4.A5.D6.A7.D8.A9.A10.C
11.
12.102+(x-1)2=x2
13.5+
14.
15.
16.(1)解:∵S梯形ABCD=a(a+b),S△EBC=b(a-b),S四边形AECD=c2,
它们满足的关系式为:a(a+b)=b(a-b)+c2,
即a2+b2=c2;
(2)解:如图2①,连接CD,作CE⊥AD于点E,
∵AD⊥AB,BC⊥AB,
∴BC=AE,CE=AB,
∴DE=AD-AE=25-16=9千米,
∴CD= =41(千米),
∴两个村庄相距41千米.
17.
18. ;
19.公路有危险需要封锁,需要封锁的路段长度为140米
20.(1);
(2);
(3).
21.(1)解:①依题意,补全图形,如图1所示.
猜想:,
理由如下:
∵,,
∴,,
∴,
②证明:如图2,在上截取,
连接
∵,,
∴是等腰直角三角形,
∴,
在和中,
∴,
∴,,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴.
(2)解:依题意补全图形,如图3所示,
在上截取,连接,
∵,,
∴,
∴,,,
∴,
∵,
∴,
∴,
在和中,
∴,
∴,,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,
∴线段,,的数量关系:.
