五年级上册数学人教版组合图形的面积(课件)(共21张PPT)
文档属性
| 名称 | 五年级上册数学人教版组合图形的面积(课件)(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 412.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
温习旧知
将下面的公式补充完整。
平行四边形的面积=( 底×高 )
三角形的面积=( 底×高÷2 )
梯形的面积=( (上底+下底)×高÷2 )
底×高
底×高÷2
(上底+下底)×高÷2
世界上的图形有很多种,如圆、三角形、梯形、正方形……这些图形对现在生活和建筑的美都做出了不可磨灭的贡献。每一种图形都有它的象征,每一种象征都有它应有的意义。无论是圆滑还是刚正,无论是稳固还是动摇,这些都会给予人联想的空间和动力,这就是人类进步的体现和开始。
预习新知
一、课前自主完成温习旧知,复习平行四边形、三角形和梯形的面积计算公式。
二、课堂中和同学了解组合图形的知识,合作探究组合图形面积的计算方法并会估算不规则图形的面积。
三、课堂中和老师一起总结出求组合图形面积的方法,并能在方格纸上估算不规则图形的面积。
第六单元 多边形的面积
组合图形的面积
五年级·数学·人教版·上册
1.认识简单的组合图形,初步了解组合图形面积的计算方法,会估算图形的面积。
2.学会正确分析图形,并能求组合图形的面积,提高运用几何知识初步解决实际问题的能力,提高观察分析的能力和解题的灵活性。
3.培养参与数学学习活动的兴趣,体会数学与自然及人类社会的密切联系。
任务驱动一
1.根据情境,回答问题。
(1)回忆我们学习了哪几种简单的平面图形及其面积的计算方法。
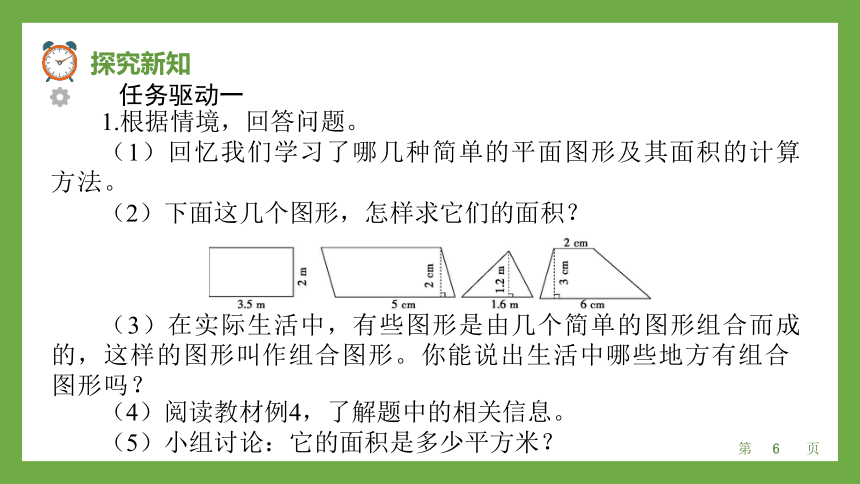
(2)下面这几个图形,怎样求它们的面积?
(3)在实际生活中,有些图形是由几个简单的图形组合而成的,这样的图形叫作组合图形。你能说出生活中哪些地方有组合图形吗?
(4)阅读教材例4,了解题中的相关信息。
(5)小组讨论:它的面积是多少平方米?
2.自主学习。
(1)尝试计算。
(2)小结。
任务驱动二
1.阅读教材例5。
(1)观察图片,了解题中的相关信息。
(2)小组讨论:怎么求这片叶子的面积?
2.规范解答。
组合图形可以通过拆分和补全来计算面积,不规则图形的面积可以转化为学过的图形的面积来估算。
一、计算下面图形的面积。(单位: cm)
1.
(9+12)×10÷2+9×9÷2=145.5(cm2)
2.
100×48+(100+36)×56÷2=8608(cm2)
二、如图中1个方格表示1 cm2,估一估下面图形的面积。( 实践类作业)
( 25.5 cm2 ) ( 17.5 cm2 )
25.5 cm2
17.5 cm2
三、求阴影部分的面积。(单位: cm)
4×(12+4)÷2=32 (cm2)
四、解决问题。
1.科技小组制作飞机模型,机翼的平面图是由两个完全相同的梯形组成的(如图)。机翼的面积是多少?
(100+48)×250÷2×2=37000(mm2)
答:机翼的面积是37000 mm2。
2.科技馆内有一架纸质飞机模型(如图所示),要粉刷这个模型的一面,且每平方米需要用0.18千克涂料,一共需要多少千克涂料?(单位:米)
(3+3+2)×3÷2=12(平方米)
2×8=16(平方米)
(2+6)×2÷2=8(平方米)
12+16+8=36(平方米)
0.18×36=6.48(千克)
答:一共需要6.48千克涂料。
二、课末总结,梳理提升
本节课学习了哪些内容?根据导学案的“知识超市”,小结本课重点内容。
归纳总结:
1.组合图形是由几个简单的图形组合而成的,其面积可以看成几个简单图形的面积和,也可以看成几个简单图形的面积差。
2.计算组合图形的面积时,要根据已知条件对图形进行分解或添补,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
三、练习拓展,内化新知
1.完成“课堂巩固”P104第一、二、三题。学生独立完成,然后集体订正。
2.课后完成“课堂巩固”P105第四题。
基础作业
一、如图,估计不规则图形的面积。(图上每个小正方形的面积为1 m2)
1.整格的一共有( 30 )格,不满整格的有( 16 )格,面积大约是( 38 )m2。
2.可以将该不规则图形近似转化成( 长方 )形。S=ah=( 5×8=40 )m2。
30
16
38
长方
5×8=40
二、计算下面图形的面积。(单位: cm)
1.6×1.5÷2+(2.8+6)×9.2÷2=44.98(cm2)
2.(4+7.2)×3.5÷2+7.2×3=41.2(cm2)
3.18×8÷2=72(cm2)
拓展作业
三、解决问题。
1.一块正六边形水泥砖(如图)可以看成是由三个相同的平行四边形组成的。要铺210平方米的地面,至少需要多少块这样的水泥砖?
17.5×20×3=1050(平方厘米)
210平方米=2100000平方厘米
2100000÷1050=2000(块)
答:至少需要2000块这样的水泥砖。
2.如图所示,在一个长10厘米、宽6厘米的零件中间,有两条宽1厘米的颜色块。没有颜色的部分的面积是多少?
10×6-1×6×2=48(cm2)
答:没有颜色的部分的面积是48平方厘米。
感谢观看 下节课再会
温习旧知
将下面的公式补充完整。
平行四边形的面积=( 底×高 )
三角形的面积=( 底×高÷2 )
梯形的面积=( (上底+下底)×高÷2 )
底×高
底×高÷2
(上底+下底)×高÷2
世界上的图形有很多种,如圆、三角形、梯形、正方形……这些图形对现在生活和建筑的美都做出了不可磨灭的贡献。每一种图形都有它的象征,每一种象征都有它应有的意义。无论是圆滑还是刚正,无论是稳固还是动摇,这些都会给予人联想的空间和动力,这就是人类进步的体现和开始。
预习新知
一、课前自主完成温习旧知,复习平行四边形、三角形和梯形的面积计算公式。
二、课堂中和同学了解组合图形的知识,合作探究组合图形面积的计算方法并会估算不规则图形的面积。
三、课堂中和老师一起总结出求组合图形面积的方法,并能在方格纸上估算不规则图形的面积。
第六单元 多边形的面积
组合图形的面积
五年级·数学·人教版·上册
1.认识简单的组合图形,初步了解组合图形面积的计算方法,会估算图形的面积。
2.学会正确分析图形,并能求组合图形的面积,提高运用几何知识初步解决实际问题的能力,提高观察分析的能力和解题的灵活性。
3.培养参与数学学习活动的兴趣,体会数学与自然及人类社会的密切联系。
任务驱动一
1.根据情境,回答问题。
(1)回忆我们学习了哪几种简单的平面图形及其面积的计算方法。
(2)下面这几个图形,怎样求它们的面积?
(3)在实际生活中,有些图形是由几个简单的图形组合而成的,这样的图形叫作组合图形。你能说出生活中哪些地方有组合图形吗?
(4)阅读教材例4,了解题中的相关信息。
(5)小组讨论:它的面积是多少平方米?
2.自主学习。
(1)尝试计算。
(2)小结。
任务驱动二
1.阅读教材例5。
(1)观察图片,了解题中的相关信息。
(2)小组讨论:怎么求这片叶子的面积?
2.规范解答。
组合图形可以通过拆分和补全来计算面积,不规则图形的面积可以转化为学过的图形的面积来估算。
一、计算下面图形的面积。(单位: cm)
1.
(9+12)×10÷2+9×9÷2=145.5(cm2)
2.
100×48+(100+36)×56÷2=8608(cm2)
二、如图中1个方格表示1 cm2,估一估下面图形的面积。( 实践类作业)
( 25.5 cm2 ) ( 17.5 cm2 )
25.5 cm2
17.5 cm2
三、求阴影部分的面积。(单位: cm)
4×(12+4)÷2=32 (cm2)
四、解决问题。
1.科技小组制作飞机模型,机翼的平面图是由两个完全相同的梯形组成的(如图)。机翼的面积是多少?
(100+48)×250÷2×2=37000(mm2)
答:机翼的面积是37000 mm2。
2.科技馆内有一架纸质飞机模型(如图所示),要粉刷这个模型的一面,且每平方米需要用0.18千克涂料,一共需要多少千克涂料?(单位:米)
(3+3+2)×3÷2=12(平方米)
2×8=16(平方米)
(2+6)×2÷2=8(平方米)
12+16+8=36(平方米)
0.18×36=6.48(千克)
答:一共需要6.48千克涂料。
二、课末总结,梳理提升
本节课学习了哪些内容?根据导学案的“知识超市”,小结本课重点内容。
归纳总结:
1.组合图形是由几个简单的图形组合而成的,其面积可以看成几个简单图形的面积和,也可以看成几个简单图形的面积差。
2.计算组合图形的面积时,要根据已知条件对图形进行分解或添补,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
三、练习拓展,内化新知
1.完成“课堂巩固”P104第一、二、三题。学生独立完成,然后集体订正。
2.课后完成“课堂巩固”P105第四题。
基础作业
一、如图,估计不规则图形的面积。(图上每个小正方形的面积为1 m2)
1.整格的一共有( 30 )格,不满整格的有( 16 )格,面积大约是( 38 )m2。
2.可以将该不规则图形近似转化成( 长方 )形。S=ah=( 5×8=40 )m2。
30
16
38
长方
5×8=40
二、计算下面图形的面积。(单位: cm)
1.6×1.5÷2+(2.8+6)×9.2÷2=44.98(cm2)
2.(4+7.2)×3.5÷2+7.2×3=41.2(cm2)
3.18×8÷2=72(cm2)
拓展作业
三、解决问题。
1.一块正六边形水泥砖(如图)可以看成是由三个相同的平行四边形组成的。要铺210平方米的地面,至少需要多少块这样的水泥砖?
17.5×20×3=1050(平方厘米)
210平方米=2100000平方厘米
2100000÷1050=2000(块)
答:至少需要2000块这样的水泥砖。
2.如图所示,在一个长10厘米、宽6厘米的零件中间,有两条宽1厘米的颜色块。没有颜色的部分的面积是多少?
10×6-1×6×2=48(cm2)
答:没有颜色的部分的面积是48平方厘米。
感谢观看 下节课再会
