人教版数学八年级下册19.1.1.1 常量与变量(含答案)
文档属性
| 名称 | 人教版数学八年级下册19.1.1.1 常量与变量(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 184.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 00:00:00 | ||
图片预览


文档简介
第十九章 一次函数
19.1 函数
第1课时 常量与变量
1.把20本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入a本,第二个抽屉放入b本,则下列判断错误的是( )
A.20是变量 B.a是变量
C.b是变量 D.20是常量
2.李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的变量是( )
A.金额
B.数量
C.单价
D.金额和数量
3.某超市进一批苹果,某日按照早、中、晚三个时间段销售,销售情况如下表,在该变化过程中,常量是( )
时间段 销售量 收入
早 100 500
中 150 750
晚 80 400
A.销售量 B.收入 C.单价 D.以上都是
4.[2023廊坊安次区期末]某工厂有一个容积为280立方米的水池,现用3台抽水机从蓄满水的池中同时抽水,已知每台抽水机每小时抽水15立方米.水池中的水量随抽水时间的变化而变化.
(1)在这一变化过程中哪些是常量?哪些是变量?
(2)抽水两小时后,池中还有水 立方米.
5.填空:
(1)某人以a米/分的速度经t分时间跑了s米,则s与t的关系式为 ,其中常量是 ,变量是 .
(2)在t分内,不同的人以不同的速度a米/分跑了s米,其中常量是 ,变量是 .
(3)s米的路程不同的人以不同的速度a米/分各需跑的时间为t分,其中常量是 ,变量是 .
(4)根据以上三句叙述,写出一句关于常量与变量的结论: .
6.[2023山西改编]如图,一种弹簧秤能称不超过10 kg的物体,不挂物体时弹簧的长为12 cm,所挂物体每增加1 kg,弹簧伸长0.5 cm,在弹性限度内,挂物体后弹簧的长度为y(cm),所挂物体的质量为x(kg),则变量x,y之间的关系式为( )
A.y=12-0.5x B.y=12+0.5x
C.y=10+0.5x D.y=0.5x
7.果子成熟后从树上落到地面,它下落的高度与经过的时间有如下的关系:
时间/秒 0.5 0.6 0.7 0.8 0.9 1
下落的高度/米 5×0.25 5× 0.36 5× 0.49 5× 0.64 5× 0.81 5× 1
如果果子经过2秒落到地上,那么此果子开始下落时离地面的高度是 米.
8.[2023长春朝阳区期末]某科技小组在网上获取了声音在空气中传播的速度与空气的温度之间的关系的一些数据如表所示.下列说法:①空气的温度越高声音传播的速度越快;②声速y与温度x之间的关系式可以是y=-0.6x+330;③温度每升高10 ℃,声速增加6 m/s,正确的有 .
温度x/℃ -20 -10 0 10 20 30
声速y/(m/s) 318 324 330 336 342 348
9.等腰三角形ABC的周长为10 cm,底边BC的长为y cm,腰AB的长为x cm.
(1)写出变量y与x之间的关系式.
(2)求x,y的取值范围.
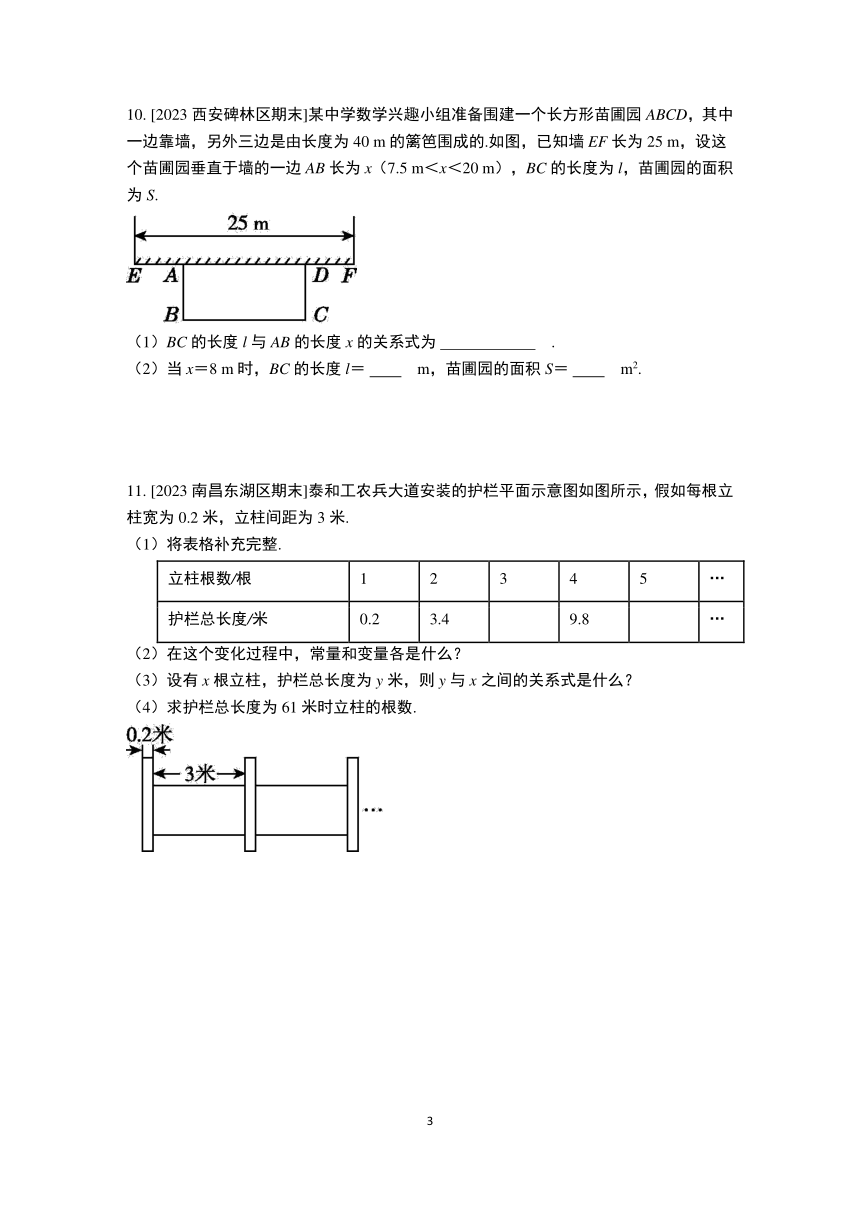
10. [2023西安碑林区期末]某中学数学兴趣小组准备围建一个长方形苗圃园ABCD,其中一边靠墙,另外三边是由长度为40 m的篱笆围成的.如图,已知墙EF长为25 m,设这个苗圃园垂直于墙的一边AB长为x(7.5 m<x<20 m),BC的长度为l,苗圃园的面积为S.
(1)BC的长度l与AB的长度x的关系式为 .
(2)当x=8 m时,BC的长度l= m,苗圃园的面积S= m2.
11. [2023南昌东湖区期末]泰和工农兵大道安装的护栏平面示意图如图所示,假如每根立柱宽为0.2米,立柱间距为3米.
(1)将表格补充完整.
立柱根数/根 1 2 3 4 5 …
护栏总长度/米 0.2 3.4 9.8 …
(2)在这个变化过程中,常量和变量各是什么?
(3)设有x根立柱,护栏总长度为y米,则y与x之间的关系式是什么?
(4)求护栏总长度为61米时立柱的根数.
12.用大小相同的黑白两种颜色的菱形纸片按照黑色纸片个数逐渐增加1的规律拼成如图所示的图案,已知“ ”的长对角线长为.
(1)第4个图案中白色纸片的个数是 ,图案的总长度为 .
(2)如果第n个图案中有y个白色纸片,写出y与n的关系式,并写出第n个图案的总长度l.
(3)当总长度为17时,求出此时图案中分别有多少个白色纸片和黑色纸片.
13.按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
14.用同样大小的黑色棋子按如图所示的规律摆放.
(1)指出这个变化过程中的变量.
(2)设第n(n为正整数)个图形中,黑色棋子的枚数为W,请你写出W与n之间的关系式.
(3)第5个图形中有多少枚黑色棋子?
(4)是否存在恰好有2 023枚黑色棋子的图形?为什么?
1
参考答案
1.A 2.D 3.C
4.解:(1)在这一变化过程中,水池的容积、抽水机的台数、每台抽水机每小时抽水的体积是常量;抽水时间、水池中的水量是变量.
(2)190
5.(1)s=at;速度a;时间t和路程s
(2)时间t;速度a和路程s (3)路程s;速度a和时间t
(4)常量和变量在一个过程中相对存在(合理即可)
6.B 7.20 8.①③
9.解:(1)由题意可得2x+y=10,所以y=10-2x.
(2)由x,y均为线段的长,可得x>0,y>0,即10-2x>0.
再由三角形三边关系,得2x>y,即2x>10-2x,
所以自变量x应满足
解这个不等式组,得<x<5.
所以0<10-2x<5,即0<y<5.
所以x的取值范围为<x<5,y的取值范围为0<y<5.
10.(1)l=40-2x (2)24;192
11.解:(1)6.6;13
(2)在这个变化过程中,常量是每根立柱的宽度和立柱间距,变量是立柱根数和护栏总长度.
(3)由题意得y与x之间的关系式为y=(0.2+3)x-3=3.2x-3.
(4)由(3)得当y=61时,3.2x-3=61,解得x=20.
答:护栏总长度为61米时立柱的根数为20.
12.解:(1)13;9
(2)如果第n个图案中有y个白色纸片,那么y与n的关系式为y=1+3n,
第n个图案的总长度l=+2n.
(3)由(2)得当总长度为17时,17=+2n,解得n=8,
∴此时白色纸片有1+3×8=25(个),黑色纸片有8个.
13.解:(1)观察图形:
x=1时,y=6;
x=2时,y=10;
x=3时,y=14;
...
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x-1)=(4x+2)个座位.
故可坐人数y=4x+2,∴题中有2个变量.
(2)能,两个变量之间的关系为y=4x+2.
14.(1)【解】变量是图形的序号与黑色棋子的枚数.
(2)【解】W与n之间的关系式为W=3n+3(n为正整数).
(3)【解】当n=5时,W=3n+3=3×5+3=18,
∴第5个图形中有18枚黑色棋子.
(4)【解】不存在.理由:设第m个图形有2 023枚黑色棋子,则3m+3=2 023,解得m=673.
∵m为正整数,∴m=673不合题意.
∴不存在恰好有2 023枚黑色棋子的图形.
19.1 函数
第1课时 常量与变量
1.把20本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入a本,第二个抽屉放入b本,则下列判断错误的是( )
A.20是变量 B.a是变量
C.b是变量 D.20是常量
2.李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的变量是( )
A.金额
B.数量
C.单价
D.金额和数量
3.某超市进一批苹果,某日按照早、中、晚三个时间段销售,销售情况如下表,在该变化过程中,常量是( )
时间段 销售量 收入
早 100 500
中 150 750
晚 80 400
A.销售量 B.收入 C.单价 D.以上都是
4.[2023廊坊安次区期末]某工厂有一个容积为280立方米的水池,现用3台抽水机从蓄满水的池中同时抽水,已知每台抽水机每小时抽水15立方米.水池中的水量随抽水时间的变化而变化.
(1)在这一变化过程中哪些是常量?哪些是变量?
(2)抽水两小时后,池中还有水 立方米.
5.填空:
(1)某人以a米/分的速度经t分时间跑了s米,则s与t的关系式为 ,其中常量是 ,变量是 .
(2)在t分内,不同的人以不同的速度a米/分跑了s米,其中常量是 ,变量是 .
(3)s米的路程不同的人以不同的速度a米/分各需跑的时间为t分,其中常量是 ,变量是 .
(4)根据以上三句叙述,写出一句关于常量与变量的结论: .
6.[2023山西改编]如图,一种弹簧秤能称不超过10 kg的物体,不挂物体时弹簧的长为12 cm,所挂物体每增加1 kg,弹簧伸长0.5 cm,在弹性限度内,挂物体后弹簧的长度为y(cm),所挂物体的质量为x(kg),则变量x,y之间的关系式为( )
A.y=12-0.5x B.y=12+0.5x
C.y=10+0.5x D.y=0.5x
7.果子成熟后从树上落到地面,它下落的高度与经过的时间有如下的关系:
时间/秒 0.5 0.6 0.7 0.8 0.9 1
下落的高度/米 5×0.25 5× 0.36 5× 0.49 5× 0.64 5× 0.81 5× 1
如果果子经过2秒落到地上,那么此果子开始下落时离地面的高度是 米.
8.[2023长春朝阳区期末]某科技小组在网上获取了声音在空气中传播的速度与空气的温度之间的关系的一些数据如表所示.下列说法:①空气的温度越高声音传播的速度越快;②声速y与温度x之间的关系式可以是y=-0.6x+330;③温度每升高10 ℃,声速增加6 m/s,正确的有 .
温度x/℃ -20 -10 0 10 20 30
声速y/(m/s) 318 324 330 336 342 348
9.等腰三角形ABC的周长为10 cm,底边BC的长为y cm,腰AB的长为x cm.
(1)写出变量y与x之间的关系式.
(2)求x,y的取值范围.
10. [2023西安碑林区期末]某中学数学兴趣小组准备围建一个长方形苗圃园ABCD,其中一边靠墙,另外三边是由长度为40 m的篱笆围成的.如图,已知墙EF长为25 m,设这个苗圃园垂直于墙的一边AB长为x(7.5 m<x<20 m),BC的长度为l,苗圃园的面积为S.
(1)BC的长度l与AB的长度x的关系式为 .
(2)当x=8 m时,BC的长度l= m,苗圃园的面积S= m2.
11. [2023南昌东湖区期末]泰和工农兵大道安装的护栏平面示意图如图所示,假如每根立柱宽为0.2米,立柱间距为3米.
(1)将表格补充完整.
立柱根数/根 1 2 3 4 5 …
护栏总长度/米 0.2 3.4 9.8 …
(2)在这个变化过程中,常量和变量各是什么?
(3)设有x根立柱,护栏总长度为y米,则y与x之间的关系式是什么?
(4)求护栏总长度为61米时立柱的根数.
12.用大小相同的黑白两种颜色的菱形纸片按照黑色纸片个数逐渐增加1的规律拼成如图所示的图案,已知“ ”的长对角线长为.
(1)第4个图案中白色纸片的个数是 ,图案的总长度为 .
(2)如果第n个图案中有y个白色纸片,写出y与n的关系式,并写出第n个图案的总长度l.
(3)当总长度为17时,求出此时图案中分别有多少个白色纸片和黑色纸片.
13.按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
14.用同样大小的黑色棋子按如图所示的规律摆放.
(1)指出这个变化过程中的变量.
(2)设第n(n为正整数)个图形中,黑色棋子的枚数为W,请你写出W与n之间的关系式.
(3)第5个图形中有多少枚黑色棋子?
(4)是否存在恰好有2 023枚黑色棋子的图形?为什么?
1
参考答案
1.A 2.D 3.C
4.解:(1)在这一变化过程中,水池的容积、抽水机的台数、每台抽水机每小时抽水的体积是常量;抽水时间、水池中的水量是变量.
(2)190
5.(1)s=at;速度a;时间t和路程s
(2)时间t;速度a和路程s (3)路程s;速度a和时间t
(4)常量和变量在一个过程中相对存在(合理即可)
6.B 7.20 8.①③
9.解:(1)由题意可得2x+y=10,所以y=10-2x.
(2)由x,y均为线段的长,可得x>0,y>0,即10-2x>0.
再由三角形三边关系,得2x>y,即2x>10-2x,
所以自变量x应满足
解这个不等式组,得<x<5.
所以0<10-2x<5,即0<y<5.
所以x的取值范围为<x<5,y的取值范围为0<y<5.
10.(1)l=40-2x (2)24;192
11.解:(1)6.6;13
(2)在这个变化过程中,常量是每根立柱的宽度和立柱间距,变量是立柱根数和护栏总长度.
(3)由题意得y与x之间的关系式为y=(0.2+3)x-3=3.2x-3.
(4)由(3)得当y=61时,3.2x-3=61,解得x=20.
答:护栏总长度为61米时立柱的根数为20.
12.解:(1)13;9
(2)如果第n个图案中有y个白色纸片,那么y与n的关系式为y=1+3n,
第n个图案的总长度l=+2n.
(3)由(2)得当总长度为17时,17=+2n,解得n=8,
∴此时白色纸片有1+3×8=25(个),黑色纸片有8个.
13.解:(1)观察图形:
x=1时,y=6;
x=2时,y=10;
x=3时,y=14;
...
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x-1)=(4x+2)个座位.
故可坐人数y=4x+2,∴题中有2个变量.
(2)能,两个变量之间的关系为y=4x+2.
14.(1)【解】变量是图形的序号与黑色棋子的枚数.
(2)【解】W与n之间的关系式为W=3n+3(n为正整数).
(3)【解】当n=5时,W=3n+3=3×5+3=18,
∴第5个图形中有18枚黑色棋子.
(4)【解】不存在.理由:设第m个图形有2 023枚黑色棋子,则3m+3=2 023,解得m=673.
∵m为正整数,∴m=673不合题意.
∴不存在恰好有2 023枚黑色棋子的图形.
