2023-2024学年人教版数学七年级下册第五章 相交线与平行线 自我评估(含答案)
文档属性
| 名称 | 2023-2024学年人教版数学七年级下册第五章 相交线与平行线 自我评估(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 370.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 00:00:00 | ||
图片预览


文档简介
第五章 相交线与平行线自我评估 2023-2024学年人教版数学七年级下册
一、单选题(共10题;共30分)
1.(3分)下列语句中是命题的有( )
①线段垂直平分线上的点到线段两端的距离相等;
②作点A关于直线l的对称点
③三边对应相等的两个三角形全等吗?
④角平分线上的点到角两边的距离相等.
A.1个 B.2个 C.3个 D.4个
2.(3分)在下列四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
3.(3分)如图,一块直角三角板的直角顶点放在直尺的一边上.如果,那么的度数是( )
A. B. C. D.
4.(3分)下列命题错误的是( )
①对角线互相垂直且平分的四边形是矩形;②对角线相等的平行四边形是矩形;③有一个角是直角的平行四边形是矩形;④有三个角是直角的四边形是矩形.
A.① B.② C.③ D.④
5.(3分)如图,如果AB∥DE,那么∠BCD=( )
A.∠2=∠1 B.∠1+∠2
C.180°+∠1-∠2 D.180°+∠2-2∠1
6.(3分)如图,小明从 处沿北偏东 方向行走至点 处,又从点 处沿东偏南 方向行走至点 处,则 等于( )
A. B. C. D.
7.(3分)如图,在一块长14m、宽6m的长方形场地上,有一条弯曲的道路,其余的部分为绿化区,道路的左边线向右平移3m就是它的右边线,则绿化区的面积是( )
A.56m2 B.66m2 C.72m2 D.96m2
8.(3分)如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )
A.7 B.8 C.9 D.10
9.(3分)如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
A.120° B.130° C.140° D.150°
10.(3分)如图,已知AB∥CD, , .则 与 之间满足的数量关系是( )
A. B.
C. D.
二、填空题(共5题;共15分)
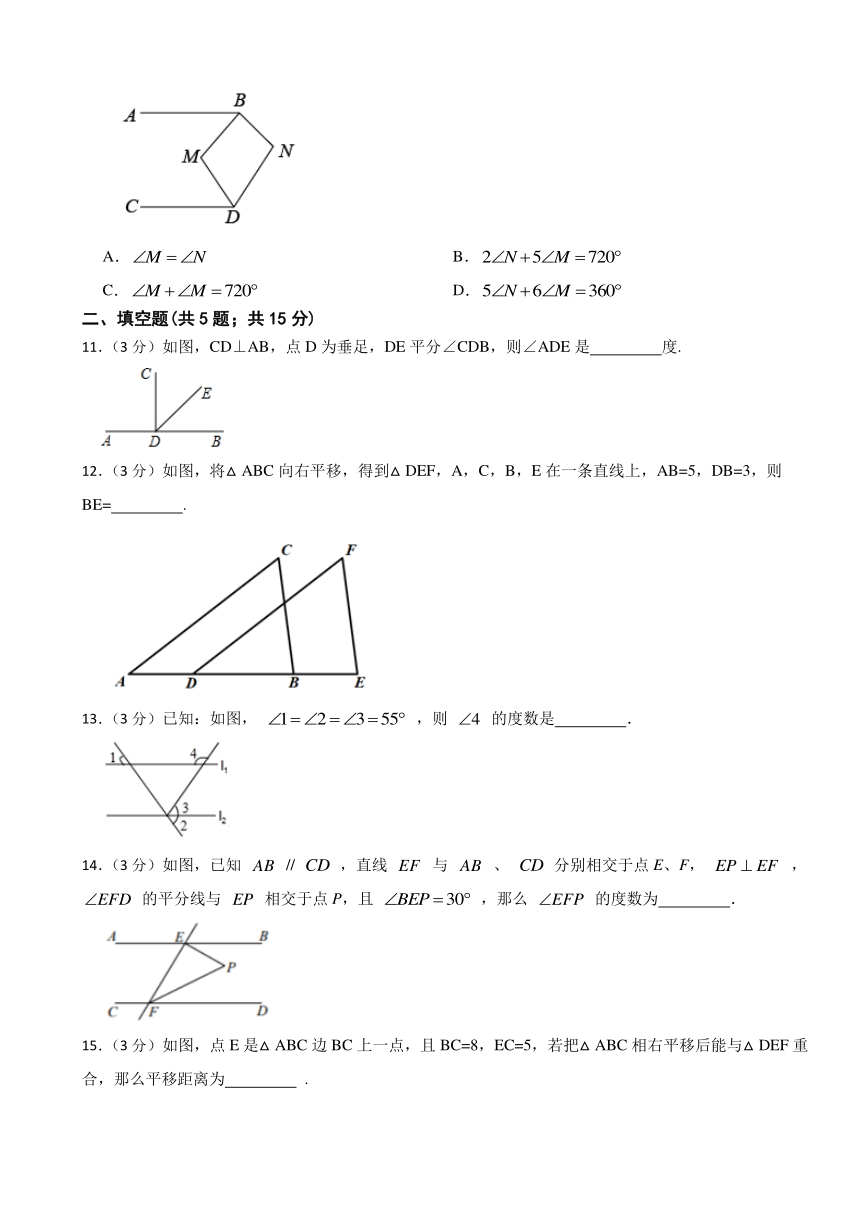
11.(3分)如图,CD⊥AB,点D为垂足,DE平分∠CDB,则∠ADE是 度.
12.(3分)如图,将△ABC向右平移,得到△DEF,A,C,B,E在一条直线上,AB=5,DB=3,则BE= .
13.(3分)已知:如图, ,则 的度数是 .
14.(3分)如图,已知 // ,直线 与 、 分别相交于点E、F, , 的平分线与 相交于点P,且 ,那么 的度数为 .
15.(3分)如图,点E是△ABC边BC上一点,且BC=8,EC=5,若把△ABC相右平移后能与△DEF重合,那么平移距离为 .
三、解答题(共7题;共55分)
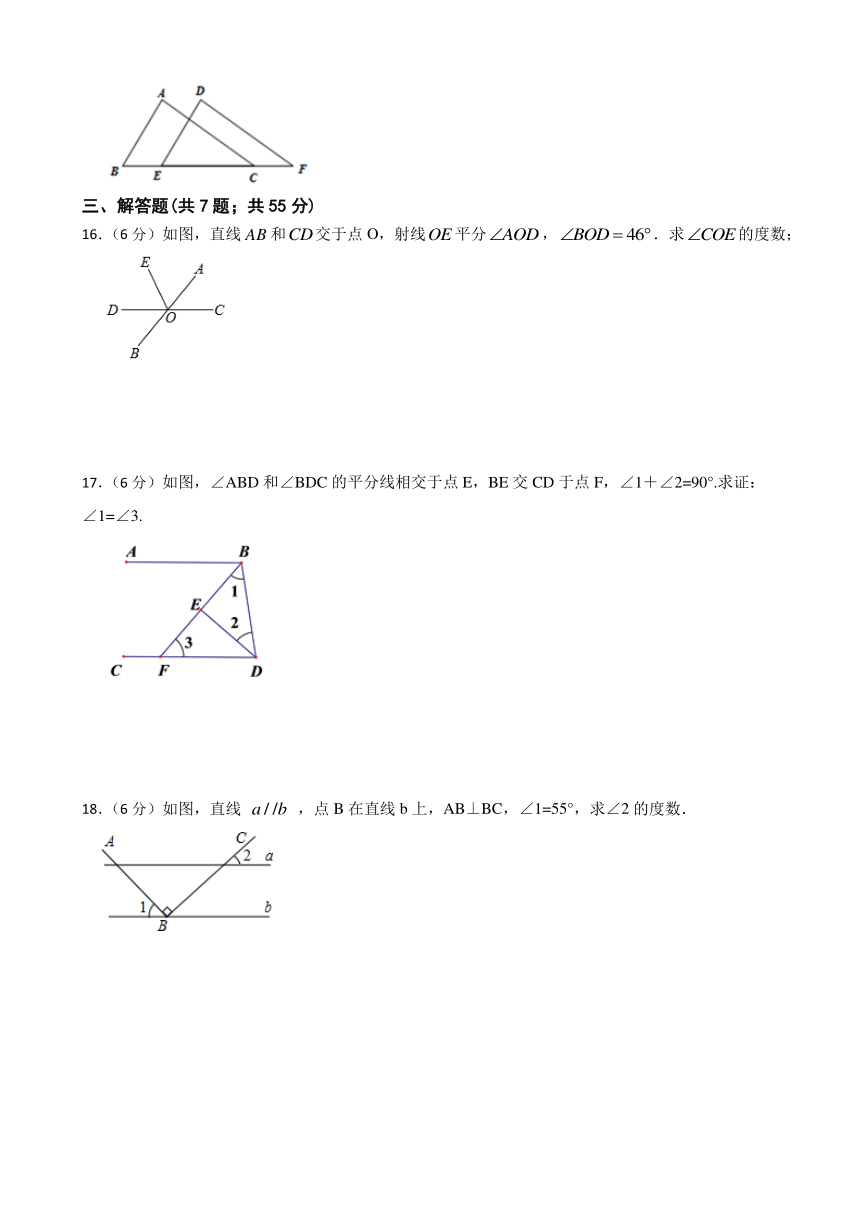
16.(6分)如图,直线和交于点O,射线平分,.求的度数;
17.(6分)如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.求证:∠1=∠3.
18.(6分)如图,直线 ,点B在直线b上,AB⊥BC,∠1=55°,求∠2的度数.
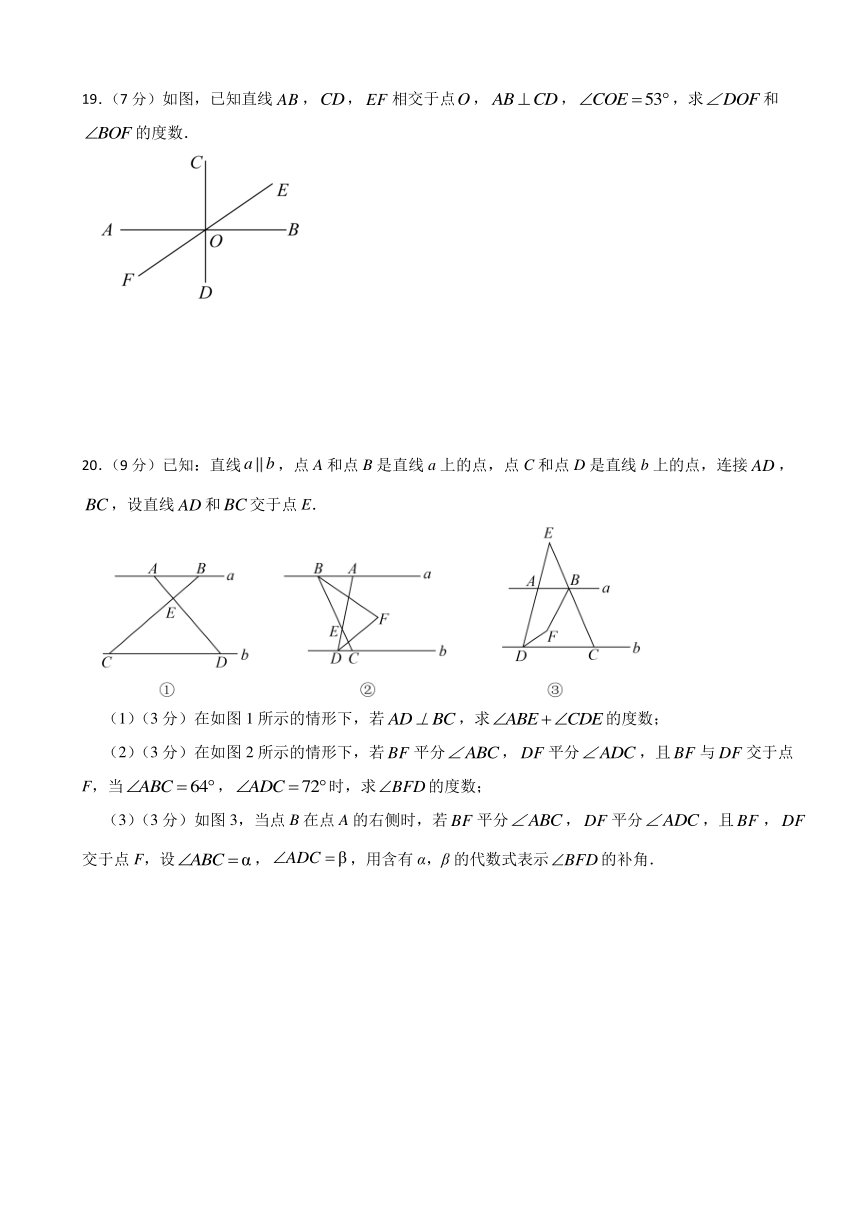
19.(7分)如图,已知直线,,相交于点,,,求和的度数.
20.(9分)已知:直线,点A和点B是直线a上的点,点C和点D是直线b上的点,连接,,设直线和交于点E.
(1)(3分)在如图1所示的情形下,若,求的度数;
(2)(3分)在如图2所示的情形下,若平分,平分,且与交于点F,当,时,求的度数;
(3)(3分)如图3,当点B在点A的右侧时,若平分,平分,且,交于点F,设,,用含有α,β的代数式表示的补角.
21.(9分)如图所示,已知射线CB∥OA,∠C= ∠OAB=100°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)(3分)求∠EOB的度数.(直接写出结果,无须解答过程)
(2)(3分)若在OC右侧左右平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,请找出变化的规律;若不变,请求出这个比值.
(3)(3分)在OC右侧左右平行移动AB的过程中,是否存在使∠OEC=∠OBA的情况?若存在,请直接写出∠OEC度数;若不存在,请说明理由.
22.(12分)如图,∠BAE +∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你完成.
解:∵∠BAE+∠AED=180°(已知)
∴AB∥DE( ).
∴∠BAE=∠AEF( ).
又∵∠1=∠2(已知)
∴ ∠BAE ∠1=∠AEF ▲ (等式性质),即 ∠MAE = ∠NEA .
∴ ▲ ∥ ▲ ( ).
∴∠M=∠N(两直线平行,内错角相等).
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
11.【答案】135
12.【答案】2
13.【答案】125°
14.【答案】30°
15.【答案】3
16.【答案】解:∵,
∴,
∵射线平分,
∴,
∴.
17.【答案】证明:∵∠ABD和∠BDC的平分线交于点E,
∴∠ABF=∠1,∠ABD=2∠1,∠BDC=2∠2,
∵∠1+∠2=90°,
∴∠ABF+∠2=90°,∠ABD+∠BDC=2×90°=180°,
∴AB∥DC,
∴∠ABF=∠3,
∴∠3+∠2=90°,
∴∠1=∠3.
18.【答案】解: ,
.
,
,
,
,
.
19.【答案】解:由对顶角性质可得:∠DOF=∠COE=53°,
∵CD⊥AB,
∴∠BOD=90°,
∴∠BOF=∠BOD+∠COE=90°+53°=143°,
∴∠DOF =53°,∠BOF=143°.
20.【答案】(1)解:过点E作,
∵,
∴,
∴,,
∴,
∵,
∴;
(2)如图,过点F作,
∵,
∴,
∴,,
∴,
∵平分,平分,,,
∴,,
∴;
(3)如图,过点F作,
∵,
∴,
∴,,
∴,
∵平分,平分,,,
∴,,
∴,
∴的补角.
21.【答案】(1)解:40°
(2)解: ∠OBC:∠OFC的值不变,理由如下:
∵ ∠FOB=∠AOB ,
∴∠AOB=∠FOA,
∵CB∥OA,
∴∠OBC=∠AOB,∠OFC=∠FOA,
∴∠OBC=∠OFC,
∴∠OBC∶∠OFC=1∶2;
(3)解:存在,∠OEC=60°.
22.【答案】解:∵∠BAE+∠AED =180° (已知)
∴AB∥DE(同旁内角互补,两直线平行)
∴ ∠BAE=∠AEF (两直线平行,内错角相等).
又∵∠1=∠2(已知)
∴∠BAE ∠1 = ∠AEF ∠2(等式性质),即∠MAE=∠NEA .
∴AM∥EN(内错角相等,两直线平行).
∴∠M=∠N(两直线平行,内错角相等).
故答案为同旁内角互补,两直线平行;两直线平行,内错角相等;∠2;AM;EN;内错角相等,两直线平行.
一、单选题(共10题;共30分)
1.(3分)下列语句中是命题的有( )
①线段垂直平分线上的点到线段两端的距离相等;
②作点A关于直线l的对称点
③三边对应相等的两个三角形全等吗?
④角平分线上的点到角两边的距离相等.
A.1个 B.2个 C.3个 D.4个
2.(3分)在下列四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
3.(3分)如图,一块直角三角板的直角顶点放在直尺的一边上.如果,那么的度数是( )
A. B. C. D.
4.(3分)下列命题错误的是( )
①对角线互相垂直且平分的四边形是矩形;②对角线相等的平行四边形是矩形;③有一个角是直角的平行四边形是矩形;④有三个角是直角的四边形是矩形.
A.① B.② C.③ D.④
5.(3分)如图,如果AB∥DE,那么∠BCD=( )
A.∠2=∠1 B.∠1+∠2
C.180°+∠1-∠2 D.180°+∠2-2∠1
6.(3分)如图,小明从 处沿北偏东 方向行走至点 处,又从点 处沿东偏南 方向行走至点 处,则 等于( )
A. B. C. D.
7.(3分)如图,在一块长14m、宽6m的长方形场地上,有一条弯曲的道路,其余的部分为绿化区,道路的左边线向右平移3m就是它的右边线,则绿化区的面积是( )
A.56m2 B.66m2 C.72m2 D.96m2
8.(3分)如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )
A.7 B.8 C.9 D.10
9.(3分)如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
A.120° B.130° C.140° D.150°
10.(3分)如图,已知AB∥CD, , .则 与 之间满足的数量关系是( )
A. B.
C. D.
二、填空题(共5题;共15分)
11.(3分)如图,CD⊥AB,点D为垂足,DE平分∠CDB,则∠ADE是 度.
12.(3分)如图,将△ABC向右平移,得到△DEF,A,C,B,E在一条直线上,AB=5,DB=3,则BE= .
13.(3分)已知:如图, ,则 的度数是 .
14.(3分)如图,已知 // ,直线 与 、 分别相交于点E、F, , 的平分线与 相交于点P,且 ,那么 的度数为 .
15.(3分)如图,点E是△ABC边BC上一点,且BC=8,EC=5,若把△ABC相右平移后能与△DEF重合,那么平移距离为 .
三、解答题(共7题;共55分)
16.(6分)如图,直线和交于点O,射线平分,.求的度数;
17.(6分)如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.求证:∠1=∠3.
18.(6分)如图,直线 ,点B在直线b上,AB⊥BC,∠1=55°,求∠2的度数.
19.(7分)如图,已知直线,,相交于点,,,求和的度数.
20.(9分)已知:直线,点A和点B是直线a上的点,点C和点D是直线b上的点,连接,,设直线和交于点E.
(1)(3分)在如图1所示的情形下,若,求的度数;
(2)(3分)在如图2所示的情形下,若平分,平分,且与交于点F,当,时,求的度数;
(3)(3分)如图3,当点B在点A的右侧时,若平分,平分,且,交于点F,设,,用含有α,β的代数式表示的补角.
21.(9分)如图所示,已知射线CB∥OA,∠C= ∠OAB=100°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)(3分)求∠EOB的度数.(直接写出结果,无须解答过程)
(2)(3分)若在OC右侧左右平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,请找出变化的规律;若不变,请求出这个比值.
(3)(3分)在OC右侧左右平行移动AB的过程中,是否存在使∠OEC=∠OBA的情况?若存在,请直接写出∠OEC度数;若不存在,请说明理由.
22.(12分)如图,∠BAE +∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你完成.
解:∵∠BAE+∠AED=180°(已知)
∴AB∥DE( ).
∴∠BAE=∠AEF( ).
又∵∠1=∠2(已知)
∴ ∠BAE ∠1=∠AEF ▲ (等式性质),即 ∠MAE = ∠NEA .
∴ ▲ ∥ ▲ ( ).
∴∠M=∠N(两直线平行,内错角相等).
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
11.【答案】135
12.【答案】2
13.【答案】125°
14.【答案】30°
15.【答案】3
16.【答案】解:∵,
∴,
∵射线平分,
∴,
∴.
17.【答案】证明:∵∠ABD和∠BDC的平分线交于点E,
∴∠ABF=∠1,∠ABD=2∠1,∠BDC=2∠2,
∵∠1+∠2=90°,
∴∠ABF+∠2=90°,∠ABD+∠BDC=2×90°=180°,
∴AB∥DC,
∴∠ABF=∠3,
∴∠3+∠2=90°,
∴∠1=∠3.
18.【答案】解: ,
.
,
,
,
,
.
19.【答案】解:由对顶角性质可得:∠DOF=∠COE=53°,
∵CD⊥AB,
∴∠BOD=90°,
∴∠BOF=∠BOD+∠COE=90°+53°=143°,
∴∠DOF =53°,∠BOF=143°.
20.【答案】(1)解:过点E作,
∵,
∴,
∴,,
∴,
∵,
∴;
(2)如图,过点F作,
∵,
∴,
∴,,
∴,
∵平分,平分,,,
∴,,
∴;
(3)如图,过点F作,
∵,
∴,
∴,,
∴,
∵平分,平分,,,
∴,,
∴,
∴的补角.
21.【答案】(1)解:40°
(2)解: ∠OBC:∠OFC的值不变,理由如下:
∵ ∠FOB=∠AOB ,
∴∠AOB=∠FOA,
∵CB∥OA,
∴∠OBC=∠AOB,∠OFC=∠FOA,
∴∠OBC=∠OFC,
∴∠OBC∶∠OFC=1∶2;
(3)解:存在,∠OEC=60°.
22.【答案】解:∵∠BAE+∠AED =180° (已知)
∴AB∥DE(同旁内角互补,两直线平行)
∴ ∠BAE=∠AEF (两直线平行,内错角相等).
又∵∠1=∠2(已知)
∴∠BAE ∠1 = ∠AEF ∠2(等式性质),即∠MAE=∠NEA .
∴AM∥EN(内错角相等,两直线平行).
∴∠M=∠N(两直线平行,内错角相等).
故答案为同旁内角互补,两直线平行;两直线平行,内错角相等;∠2;AM;EN;内错角相等,两直线平行.
