五年级下册数学人教版真分数和假分数(课件)(共22张PPT)
文档属性
| 名称 | 五年级下册数学人教版真分数和假分数(课件)(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 852.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 14:13:02 | ||
图片预览





文档简介
(共22张PPT)
温习旧知
写出7个分数单位是 的分数。
(答案不唯一)
分数 与整数2在数值上相等,但二者在意义上有所不同。分数 表
示把单位“1”平均分成2份,有这样的4份;整数2表示2个单位
“1”。
预习新知
一、课前自学教材例1、例2、例3的内容,完成“温习旧知”,复习
分数单位的知识。
二、课中和同学合作探究真分数和假分数的特征。
三、课中和老师一起总结真分数和假分数的特征,并学会假分数和带
分数(或整数)的互化。
第四单元 分数的意义和性质
真分数和假分数
五年级·数学·人教版·下册
1. 理解真分数和假分数的意义,并掌握其特征。
2. 认识带分数,并能把假分数化成带分数或整数。
3. 能在直线上把分数表示出来,体会数形结合的数学思想。
任务驱动一:用涂一涂的方法分别表示下列分数,并解答以下问
题。
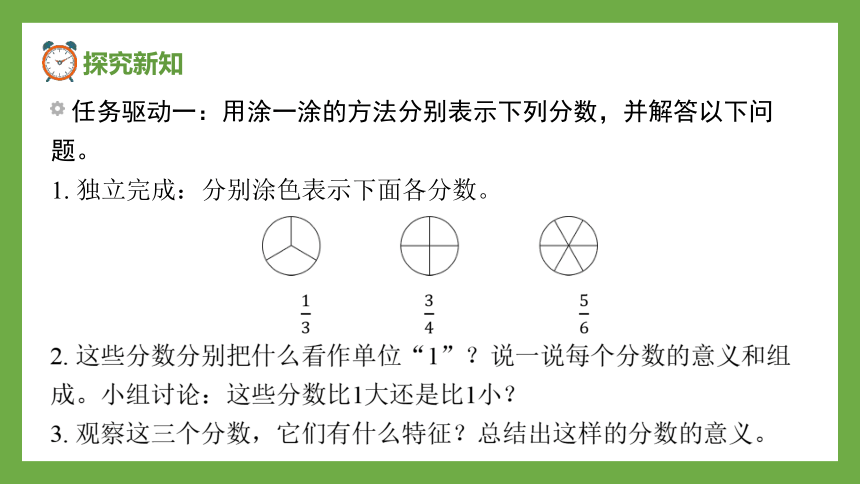
1. 独立完成:分别涂色表示下面各分数。
2. 这些分数分别把什么看作单位“1”?说一说每个分数的意义和组
成。小组讨论:这些分数比1大还是比1小?
3. 观察这三个分数,它们有什么特征?总结出这样的分数的意义。
任务驱动二:把一个圆看作单位“1”,用涂一涂的方法表示下列
分数,并解答以下问题。
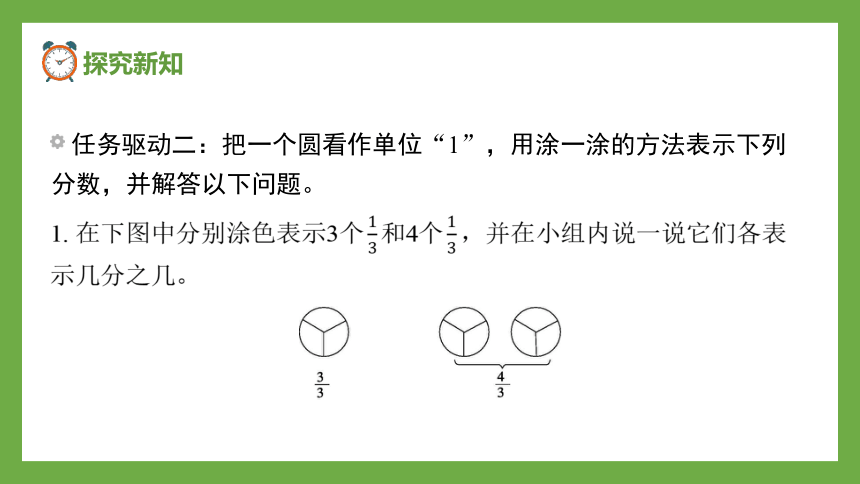
1. 在下图中分别涂色表示3个 和4个 ,并在小组内说一说它们各表
示几分之几。
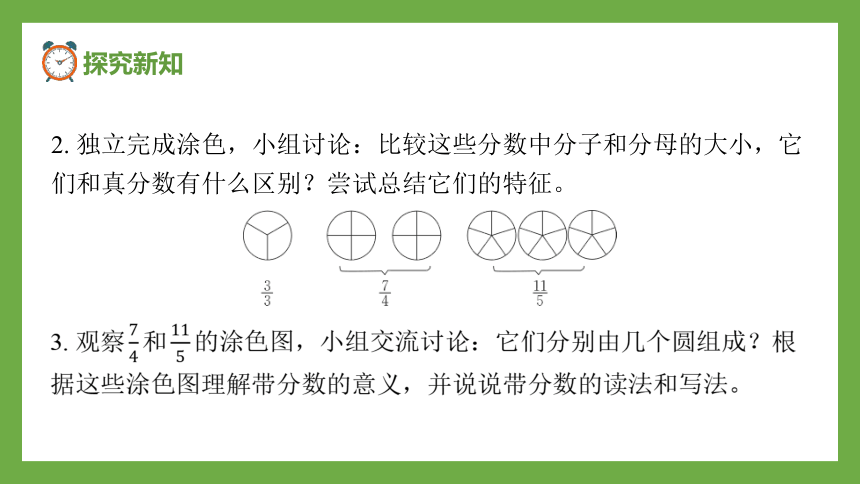
2. 独立完成涂色,小组讨论:比较这些分数中分子和分母的大小,它
们和真分数有什么区别?尝试总结它们的特征。
3. 观察 和 的涂色图,小组交流讨论:它们分别由几个圆组成?根
据这些涂色图理解带分数的意义,并说说带分数的读法和写法。
任务驱动三:根据分数的意义和分数与除法的关系,解答下面的问
题。
1. 小组合作,用自己的方法把 、 化成整数,并把你的方法写出
来。
(1)根据分数的意义画图理解。
(2)根据分数与除法的关系,用“分子除以分母”进行计算。
2. 怎样把 、 化成带分数?
(1)根据分数的意义画图理解。
(2)根据分数与除法的关系,用“分子除以分母”进行计算。
1. 分子比分母小的分数叫作真分数,真分数小于1。
2. 分子比分母大或分子和分母相等的分数叫作假分数,假分数大
于或等于1。
3. 假分数化成整数或带分数的方法:用分子除以分母,当分子是
分母的整数倍时,能化成整数,商就是这个整数;当分子不是分母的
整数倍时,能化成带分数,商是带分数的整数部分,余数是分数部分
的分子,分母不变。
一、用假分数和带分数表示出各图涂色部分的大小。
假分数:( ) 假分数:( ) 假分数:( )
带分数:( 1 ) 带分数:( 3 ) 带分数:( 2 )
1
3
2
二、填空。
1. 分母是5的所有真分数有( , , , )。
2. 分子是6的所有假分数有( , , , , , )。
3. 若 是假分数, 是真分数,则整数a应该是( 16 )。
4. 分数单位是 的最小假分数是( ),最大真分数是(
),最小带分数是( 1 )。
, , ,
, , , , ,
16
1
三、把下面的假分数化成带分数或整数。
=2 =3 =4 =40
2
3
4
40
四、在直线上面的 里填上适当的假分数,在直线下面的 里填上
适当的带分数。
2
3
4
五、北京是世界上第一个举办夏季奥运会和冬季奥运会的“双奥之
城”,实现了中国奥运的百年梦想,开启了奥林匹克新起点,成为国
际奥林匹克文化传播中心和世界文明交流互鉴的大舞台。在2022年北
京冬奥会中,假设一个国家参加冬奥会的男、女运动员人数分别为 a
和 b 。( 拓展类作业)
1. 男运动员人数是女运动员人数的 ,若 是一个真分数,则说
明 。
2. 男运动员人数占总人数的 ,若 是一个假分数,则说
明 。
这个国家参加冬奥会的男运动员人数比女运动员人数少
这个国家参加冬奥会的运动员都是男运动员
六、举例说一说把假分数化成带分数或整数的方法。( 实践类作
业)
略
基础作业
一、把一个图形看作单位“1”,用分数表示涂色部分。
( ) ( )
这两个分数的分子比分母( 大 )或与分母( 相等 ),都是
( 假分数 ),分数值比1( 大 )或( 等于 )1。
大
相等
假分数
大
等于
二、下面哪些分数是真分数?哪些分数是假分数?填在相应的圈里。
,
三、在 (a≠0)中,根据所给条件确定a是什么数。
1. 当 a ( <9 )时, 是真分数。
2. 当 a ( ≥9 )时, 是假分数。
3. 当 a ( 是9的倍数 )时, 能化成整数。
4. 当 a ( =10 )时, 能化成分数单位是 的最小带分数。
<9
≥9
是9的倍数
=10
拓展作业
四、一个带分数的分子、分母和整数部分是3个连续的自然数,整数
部分的自然数最大,且是3的倍数中的最大的一位数,这个带分数写
成假分数是多少?
。
感谢观看 下节课再会
温习旧知
写出7个分数单位是 的分数。
(答案不唯一)
分数 与整数2在数值上相等,但二者在意义上有所不同。分数 表
示把单位“1”平均分成2份,有这样的4份;整数2表示2个单位
“1”。
预习新知
一、课前自学教材例1、例2、例3的内容,完成“温习旧知”,复习
分数单位的知识。
二、课中和同学合作探究真分数和假分数的特征。
三、课中和老师一起总结真分数和假分数的特征,并学会假分数和带
分数(或整数)的互化。
第四单元 分数的意义和性质
真分数和假分数
五年级·数学·人教版·下册
1. 理解真分数和假分数的意义,并掌握其特征。
2. 认识带分数,并能把假分数化成带分数或整数。
3. 能在直线上把分数表示出来,体会数形结合的数学思想。
任务驱动一:用涂一涂的方法分别表示下列分数,并解答以下问
题。
1. 独立完成:分别涂色表示下面各分数。
2. 这些分数分别把什么看作单位“1”?说一说每个分数的意义和组
成。小组讨论:这些分数比1大还是比1小?
3. 观察这三个分数,它们有什么特征?总结出这样的分数的意义。
任务驱动二:把一个圆看作单位“1”,用涂一涂的方法表示下列
分数,并解答以下问题。
1. 在下图中分别涂色表示3个 和4个 ,并在小组内说一说它们各表
示几分之几。
2. 独立完成涂色,小组讨论:比较这些分数中分子和分母的大小,它
们和真分数有什么区别?尝试总结它们的特征。
3. 观察 和 的涂色图,小组交流讨论:它们分别由几个圆组成?根
据这些涂色图理解带分数的意义,并说说带分数的读法和写法。
任务驱动三:根据分数的意义和分数与除法的关系,解答下面的问
题。
1. 小组合作,用自己的方法把 、 化成整数,并把你的方法写出
来。
(1)根据分数的意义画图理解。
(2)根据分数与除法的关系,用“分子除以分母”进行计算。
2. 怎样把 、 化成带分数?
(1)根据分数的意义画图理解。
(2)根据分数与除法的关系,用“分子除以分母”进行计算。
1. 分子比分母小的分数叫作真分数,真分数小于1。
2. 分子比分母大或分子和分母相等的分数叫作假分数,假分数大
于或等于1。
3. 假分数化成整数或带分数的方法:用分子除以分母,当分子是
分母的整数倍时,能化成整数,商就是这个整数;当分子不是分母的
整数倍时,能化成带分数,商是带分数的整数部分,余数是分数部分
的分子,分母不变。
一、用假分数和带分数表示出各图涂色部分的大小。
假分数:( ) 假分数:( ) 假分数:( )
带分数:( 1 ) 带分数:( 3 ) 带分数:( 2 )
1
3
2
二、填空。
1. 分母是5的所有真分数有( , , , )。
2. 分子是6的所有假分数有( , , , , , )。
3. 若 是假分数, 是真分数,则整数a应该是( 16 )。
4. 分数单位是 的最小假分数是( ),最大真分数是(
),最小带分数是( 1 )。
, , ,
, , , , ,
16
1
三、把下面的假分数化成带分数或整数。
=2 =3 =4 =40
2
3
4
40
四、在直线上面的 里填上适当的假分数,在直线下面的 里填上
适当的带分数。
2
3
4
五、北京是世界上第一个举办夏季奥运会和冬季奥运会的“双奥之
城”,实现了中国奥运的百年梦想,开启了奥林匹克新起点,成为国
际奥林匹克文化传播中心和世界文明交流互鉴的大舞台。在2022年北
京冬奥会中,假设一个国家参加冬奥会的男、女运动员人数分别为 a
和 b 。( 拓展类作业)
1. 男运动员人数是女运动员人数的 ,若 是一个真分数,则说
明 。
2. 男运动员人数占总人数的 ,若 是一个假分数,则说
明 。
这个国家参加冬奥会的男运动员人数比女运动员人数少
这个国家参加冬奥会的运动员都是男运动员
六、举例说一说把假分数化成带分数或整数的方法。( 实践类作
业)
略
基础作业
一、把一个图形看作单位“1”,用分数表示涂色部分。
( ) ( )
这两个分数的分子比分母( 大 )或与分母( 相等 ),都是
( 假分数 ),分数值比1( 大 )或( 等于 )1。
大
相等
假分数
大
等于
二、下面哪些分数是真分数?哪些分数是假分数?填在相应的圈里。
,
三、在 (a≠0)中,根据所给条件确定a是什么数。
1. 当 a ( <9 )时, 是真分数。
2. 当 a ( ≥9 )时, 是假分数。
3. 当 a ( 是9的倍数 )时, 能化成整数。
4. 当 a ( =10 )时, 能化成分数单位是 的最小带分数。
<9
≥9
是9的倍数
=10
拓展作业
四、一个带分数的分子、分母和整数部分是3个连续的自然数,整数
部分的自然数最大,且是3的倍数中的最大的一位数,这个带分数写
成假分数是多少?
。
感谢观看 下节课再会
