数学人教A版(2019)选择性必修第二册4.1.1数列的概念 课件(共34张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.1.1数列的概念 课件(共34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-25 16:55:32 | ||
图片预览









文档简介
(共34张PPT)
4.1.1 数列的概念
教学目标:
1.了解数列的概念、表示方法,培养数学抽象素养;
2.了解数列与函数之间的关系,类比函数的研究路径,为后面的数列研究提供思路引导.
第一课时
实例1
记王芳第i岁时的身高为hi,则h1=75,h2=87,…,h17=168.
hi中的i反映了身高按岁数从1到17的顺序排列时的确定位置.
这17个身高数据不能交换位置
①是具有确定顺序的一列数
1.王芳从1岁到17岁,每年生日那天都测量身高.将这些身高数据(单位:cm)一次排成一列数:
75,87,96,103,110,116,120,128,138,
145,153,158,160,162,163,165,168.
①
问题: h5,h10能否交换位置?具有确定的顺序吗?
实例2
记第i天月亮可见部分的数为si,则s1=5,s2=10,…,s15=240.
si中的i反映了月亮可见部分的数按日期从1到15的顺序排列时的确定位置.
这15个数之间不能交换位置
②是具有确定顺序的一列数
2.在两河流域发掘的一块泥板(编号K90,约产生于公元前7世纪)上,有一列依次表示15天中从第一天到第15天每天月亮可见部分的数:
5,10,20,40,80,96,112,128,
144,160,176,192,208,224,240
②
实例3
[思考1]仿照前面的叙述,说明③也是具有确定顺序的一列数.
③
共同特征:顺序确定
[思考2]上述三个例子的共同特征是什么?
一列数
确定顺序
75,87,96,103,110,116,120,128,138,145,153,158,160,162,163,165,168.
①
5,10,20,40,80,96,112,128,144,160,176,192,208,224,240.
②
③
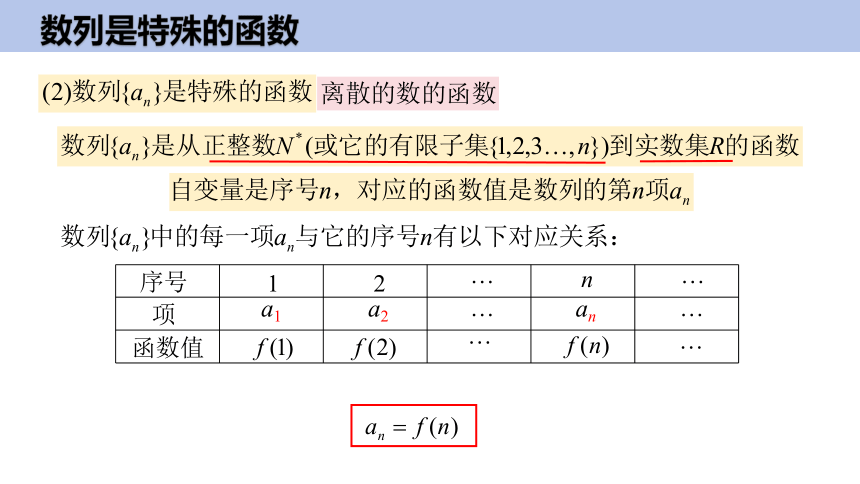
数列的概念
1.概念:
(1)数列的一般形式:
如:记王芳第i岁时的身高为ai,则a175,a287,a396,…,a17168.
a1
a2
an
数列是特殊的函数
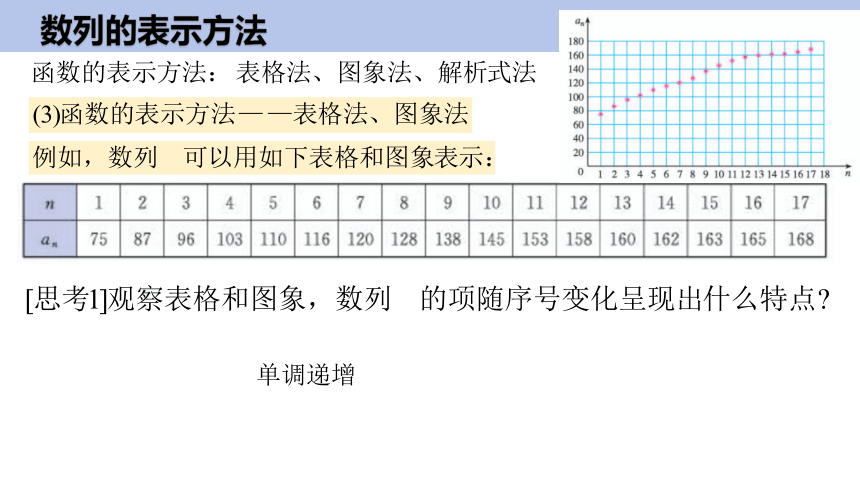
数列的表示方法
单调递增
以序号为横坐标,相应的项为纵坐标,数列的图象是由一些孤立的点构成的.
(4)数列的分类:
(i)按单调性分类:递增数列、递减数列、常数列、摆动数列
(ii)按项数是否有限分类:有穷数列和无穷数列
递增数列:从第2项起,每一项都大于它的前一项
递减数列:从第2项起,每一项都小于它的前一项
常 数 列:各项都相等的数列
摆动数列:从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列
如:2,4,6,8,10,…
如:2,3,2,5,2,7,…
如:1,,,,,…
如:1,1,1,1,…
对任意n∈N*,总有an+1>an (或an+1-an>0)
对任意n∈N*,总有an+1数列的分类
数列的表示方法
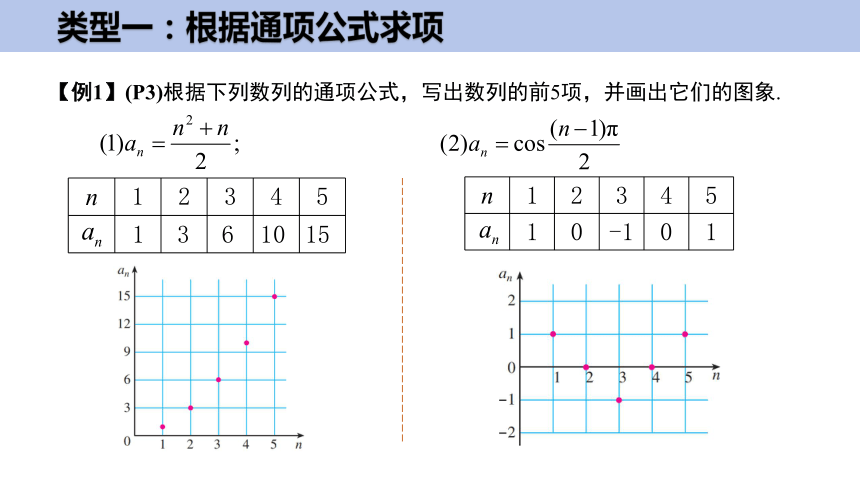
类型一:根据通项公式求项
【例1】(P3)根据下列数列的通项公式,写出数列的前5项,并画出它们的图象.
n 1 2 3 4 5
1 3 6 10 15
n 1 2 3 4 5
1 0 -1 0 1
类型一:根据通项公式求项
[练习1](P8)根据数列{an}的通项公式填表:
【例2】根据下列数列的前4项或前5项,写出数列的一个通项公式.
一些数列的通项公式不是唯一的.
不是每一个数列都能写出它的通项公式.
如:1,24,8,3,19
类型二:根据项求通项公式
总结
1.数列的概念——数学抽象
2.数列的表示方法——类比函数
3.数列的分类
4.通项公式——数学抽象、数学运算
5.计算技巧:
教学目标:
1.了解数列的递推公式,培养逻辑推理、数学运算素养;
2.了解数列的前n项和,培养数学运算素养.
第二课时
类型三:通项公式的应用
1
3
9
27
【例4】(P8)图中的一系列三角形图案称为谢尔宾斯基三角形. 在图中4个大三角形中, 着色的三角形的个数依次构成一个数列的前4项, 写出这个数列的一个通项公式.
问题1:项与项之间有什么关系?
×3
×3
×3
新知二:递推公式
表示方法:表格、图象、通项公式、递推公式
作用: 知道了首项和递推公式,就能求出数列的每一项了.
递推公式
通项公式
项与序号之间的关系:
相邻几项之间的关系:
(n≥2)
如何研究一列数的取值规律?
1.对于取值规律比较明显的数列,可以通过观察、猜测得出数列的整体规律:
2.对于取值规律不明显的数列,可以通过运算进行代数推理而得出规律.如依次取出数列的某一项,减去或除以它的前一项,再对差或商加以观察.
反思总结
新知二:递推公式
【例5】根据下列条件, 写出数列{an}的前5项:
类型四:递推公式
新知三:前n项和
Sn 与an的关系式
新知三:前n项和
验证
若满足,则合并
若不满足,则分段
已知Sn求an的3个步骤
(1)先利用a1=S1求出a1;
(2)用n-1替换Sn中的n得到一个新的关系,利用an=Sn-Sn-1(n≥2)便可求出当n≥2时an的表达式;
(3)对n=1时的结果进行检验,看是否符合n≥2时an的表达式,如果符合,则可以把数列的通项公式合写;如果不符合,则应该分n=1与n≥2两段来写.
反思总结
类型五:由Sn求an
总结
1.数列的概念、分类和表示方法
2.递推公式
3.前n项和
数学抽象、逻辑推理、数学运算
用数学的眼光观察现实世界
用数学的思维思考现实世界
用数学的语言表达现实世界
[拓展]斐波那契数列
课本P9-4.已知数列{an}满足a1=1,a2=2,以后各项由an=an-1 +an-2(n≥3)给出,
则数列的前9项分别是________________________________.
1, 2, 3, 5, 8, 13, 21, 34, 55
斐波那契数列(又称黄金分割数列):1,1,2, 3, 5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,……
①an=an-1 +an-2(n≥3):从第3项开始,每一项都等于前两项之和;
向日葵花盘上的螺旋线条,
顺时针的螺旋线:21条;
逆时针的螺旋线:34条。
斐波那契数与向日葵
斐波那契数与松果
松果上的螺旋线条,
顺时针的螺旋线:8条;
逆时针的螺旋线:13条。
斐波那契数与海螺
斐波那契螺旋线
绘制斐波那契螺旋线,验证课本P11的结论
{an}: 1,1, 2, 3, 5, 8, 13, 21, 34, 55,…
+…+
随着边长的增加,螺旋线的形状越来越接近“黄金比例螺旋”.
前n个小正方形的面积和为相邻两个斐波那契数an与an+1之积
(n≥2)
斐波那契在《算盘书》中的兔子繁殖问题(兔子数单位:对)
如果1对兔子每月能生1对小兔子(一雄一雌),而每1对小兔子在它出生后的第3个月里,又能生1对小兔子,假定在不发生死亡的情况下,由1对初生的小兔子开始,50个月后会有多少对兔子
未完待续……
4.1.1 数列的概念
教学目标:
1.了解数列的概念、表示方法,培养数学抽象素养;
2.了解数列与函数之间的关系,类比函数的研究路径,为后面的数列研究提供思路引导.
第一课时
实例1
记王芳第i岁时的身高为hi,则h1=75,h2=87,…,h17=168.
hi中的i反映了身高按岁数从1到17的顺序排列时的确定位置.
这17个身高数据不能交换位置
①是具有确定顺序的一列数
1.王芳从1岁到17岁,每年生日那天都测量身高.将这些身高数据(单位:cm)一次排成一列数:
75,87,96,103,110,116,120,128,138,
145,153,158,160,162,163,165,168.
①
问题: h5,h10能否交换位置?具有确定的顺序吗?
实例2
记第i天月亮可见部分的数为si,则s1=5,s2=10,…,s15=240.
si中的i反映了月亮可见部分的数按日期从1到15的顺序排列时的确定位置.
这15个数之间不能交换位置
②是具有确定顺序的一列数
2.在两河流域发掘的一块泥板(编号K90,约产生于公元前7世纪)上,有一列依次表示15天中从第一天到第15天每天月亮可见部分的数:
5,10,20,40,80,96,112,128,
144,160,176,192,208,224,240
②
实例3
[思考1]仿照前面的叙述,说明③也是具有确定顺序的一列数.
③
共同特征:顺序确定
[思考2]上述三个例子的共同特征是什么?
一列数
确定顺序
75,87,96,103,110,116,120,128,138,145,153,158,160,162,163,165,168.
①
5,10,20,40,80,96,112,128,144,160,176,192,208,224,240.
②
③
数列的概念
1.概念:
(1)数列的一般形式:
如:记王芳第i岁时的身高为ai,则a175,a287,a396,…,a17168.
a1
a2
an
数列是特殊的函数
数列的表示方法
单调递增
以序号为横坐标,相应的项为纵坐标,数列的图象是由一些孤立的点构成的.
(4)数列的分类:
(i)按单调性分类:递增数列、递减数列、常数列、摆动数列
(ii)按项数是否有限分类:有穷数列和无穷数列
递增数列:从第2项起,每一项都大于它的前一项
递减数列:从第2项起,每一项都小于它的前一项
常 数 列:各项都相等的数列
摆动数列:从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列
如:2,4,6,8,10,…
如:2,3,2,5,2,7,…
如:1,,,,,…
如:1,1,1,1,…
对任意n∈N*,总有an+1>an (或an+1-an>0)
对任意n∈N*,总有an+1
数列的表示方法
类型一:根据通项公式求项
【例1】(P3)根据下列数列的通项公式,写出数列的前5项,并画出它们的图象.
n 1 2 3 4 5
1 3 6 10 15
n 1 2 3 4 5
1 0 -1 0 1
类型一:根据通项公式求项
[练习1](P8)根据数列{an}的通项公式填表:
【例2】根据下列数列的前4项或前5项,写出数列的一个通项公式.
一些数列的通项公式不是唯一的.
不是每一个数列都能写出它的通项公式.
如:1,24,8,3,19
类型二:根据项求通项公式
总结
1.数列的概念——数学抽象
2.数列的表示方法——类比函数
3.数列的分类
4.通项公式——数学抽象、数学运算
5.计算技巧:
教学目标:
1.了解数列的递推公式,培养逻辑推理、数学运算素养;
2.了解数列的前n项和,培养数学运算素养.
第二课时
类型三:通项公式的应用
1
3
9
27
【例4】(P8)图中的一系列三角形图案称为谢尔宾斯基三角形. 在图中4个大三角形中, 着色的三角形的个数依次构成一个数列的前4项, 写出这个数列的一个通项公式.
问题1:项与项之间有什么关系?
×3
×3
×3
新知二:递推公式
表示方法:表格、图象、通项公式、递推公式
作用: 知道了首项和递推公式,就能求出数列的每一项了.
递推公式
通项公式
项与序号之间的关系:
相邻几项之间的关系:
(n≥2)
如何研究一列数的取值规律?
1.对于取值规律比较明显的数列,可以通过观察、猜测得出数列的整体规律:
2.对于取值规律不明显的数列,可以通过运算进行代数推理而得出规律.如依次取出数列的某一项,减去或除以它的前一项,再对差或商加以观察.
反思总结
新知二:递推公式
【例5】根据下列条件, 写出数列{an}的前5项:
类型四:递推公式
新知三:前n项和
Sn 与an的关系式
新知三:前n项和
验证
若满足,则合并
若不满足,则分段
已知Sn求an的3个步骤
(1)先利用a1=S1求出a1;
(2)用n-1替换Sn中的n得到一个新的关系,利用an=Sn-Sn-1(n≥2)便可求出当n≥2时an的表达式;
(3)对n=1时的结果进行检验,看是否符合n≥2时an的表达式,如果符合,则可以把数列的通项公式合写;如果不符合,则应该分n=1与n≥2两段来写.
反思总结
类型五:由Sn求an
总结
1.数列的概念、分类和表示方法
2.递推公式
3.前n项和
数学抽象、逻辑推理、数学运算
用数学的眼光观察现实世界
用数学的思维思考现实世界
用数学的语言表达现实世界
[拓展]斐波那契数列
课本P9-4.已知数列{an}满足a1=1,a2=2,以后各项由an=an-1 +an-2(n≥3)给出,
则数列的前9项分别是________________________________.
1, 2, 3, 5, 8, 13, 21, 34, 55
斐波那契数列(又称黄金分割数列):1,1,2, 3, 5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,……
①an=an-1 +an-2(n≥3):从第3项开始,每一项都等于前两项之和;
向日葵花盘上的螺旋线条,
顺时针的螺旋线:21条;
逆时针的螺旋线:34条。
斐波那契数与向日葵
斐波那契数与松果
松果上的螺旋线条,
顺时针的螺旋线:8条;
逆时针的螺旋线:13条。
斐波那契数与海螺
斐波那契螺旋线
绘制斐波那契螺旋线,验证课本P11的结论
{an}: 1,1, 2, 3, 5, 8, 13, 21, 34, 55,…
+…+
随着边长的增加,螺旋线的形状越来越接近“黄金比例螺旋”.
前n个小正方形的面积和为相邻两个斐波那契数an与an+1之积
(n≥2)
斐波那契在《算盘书》中的兔子繁殖问题(兔子数单位:对)
如果1对兔子每月能生1对小兔子(一雄一雌),而每1对小兔子在它出生后的第3个月里,又能生1对小兔子,假定在不发生死亡的情况下,由1对初生的小兔子开始,50个月后会有多少对兔子
未完待续……
