高中物理 教科版必修1 第四章第2节《共点力平衡条件的应用》教案
文档属性
| 名称 | 高中物理 教科版必修1 第四章第2节《共点力平衡条件的应用》教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 604.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2015-08-14 10:58:15 | ||
图片预览




文档简介
习题课:共点力平衡条件的应用
[目标定位]
1.进一步理解共点力作用下物体的平衡条件.
2.掌握矢量三角形法解共点力作用下的平衡问题.3.掌握动态平衡问题的分析方法.4.掌握整体法和隔离法分析连接体平衡问题.
( http: / / www.21cnjy.com )
一、矢量三角形法(合成法)求解共点力平衡问题
物体受多力作用处于平衡状态时,可用正交分 ( http: / / www.21cnjy.com )解法求解,但当物体受三个力作用而平衡时,可用矢量三角形法,即其中任意两个力的合力与第三个力大小相等、方向相反,且这三个力首尾相接构成封闭三角形,通过解三角形求解相应力的大小和方向,当这三个力组成含有特殊角(60°、53°、45°)的直角三角形时尤为简单.
例1 在科学研究中,可以用风力仪直接测量风力的大小,其原理如图1所示.仪器中一根轻质金属丝,悬挂着一个金属球.无风时,金属丝竖直下垂;当受到沿水平方向吹来的风时,金属丝偏离竖直方向一个角度.风力越大,偏角越大,通过传感器,就可以根据偏角的大小指示出风力的大小,那么风力大小F跟金属球的质量m、偏角θ之间有什么样的关系呢?(试用矢量三角形法和正交分解法两种方法求解)
( http: / / www.21cnjy.com )
图1
解析 取金属球为研究对象,有风时,它受到三 ( http: / / www.21cnjy.com )个力的作用:重力mg、水平方向的风力F和金属丝的拉力T,如图甲所示.这三个力是共点力,在这三个共点力的作用下金属球处于平衡状态,则这三个力的合力为零,可以根据任意两力的合力与第三个力等大、反向求解,也可以用正交分解法求解.
( http: / / www.21cnjy.com )
甲
解法一 矢量三角形法
如图乙所示,风力F和拉力T的合力与重力等大反向,由矢量三角形可得:F=mgtan θ.
( http: / / www.21cnjy.com )
解法二 正交分解法
以金属球为坐标原点,取水平方向为x轴,竖直 ( http: / / www.21cnjy.com )方向为y轴,建立直角坐标系,如图丙所示.有水平方向的合力Fx合和竖直方向的合力Fy合分别等于零,即
Fx合=Tsin θ-F=0,Fy合=Tcos θ-mg=0,
解得F=mgtan θ.由所得结果可见,当金属球的质量m一定时,风力F只跟偏角θ有关.因此,根据偏角θ的大小就可以指示出风力的大小.
答案 F=mgtan θ
针对训练 如图2所示,光滑 ( http: / / www.21cnjy.com )半球形容器固定在水平面上,O为球心,一质量为m的小滑块,在水平力F的作用下静止于P点,设滑块所受支持力为N,OP与水平方向的夹角为θ,下列关系正确的是( )
图2
A.F= B.F=mgtan θ
C.N= D.N=mgtan θ
答案 A
解析 对滑块进行受力分析如图,滑块受到 ( http: / / www.21cnjy.com )重力mg、支持力N、水平推力F三个力作用.由共点力的平衡条件知,F与mg的合力F′与N等大、反向.根据平行四边形定则可知N、mg和合力F′构成直角三角形,解直角三角形可求得:F=,N=.所以正确选项为A.
( http: / / www.21cnjy.com )
二、动态平衡问题
所谓动态平衡问题是指通过控制某些物 ( http: / / www.21cnjy.com )理量,使物体的状态发生缓慢变化,而在这个过程中物体又始终处于一系列的平衡状态,这类问题的解决方法一般用图解法和相似三角形法.
1.图解法
(1)特征:物体受三个力作用,这三 ( http: / / www.21cnjy.com )个力中,一个是恒力,大小、方向均不变化,另两个是变力,其中一个是方向不变的力,另一个是大小、方向均变化的力.
(2)处理方法:把这三个力平移到一个矢量三角形中,利用图解法判断两个变力大小、方向的变化.
2.相似三角形法
(1)特征:物体一般也受三个力作用,这三个力中,一个是恒力,另两个是大小、方向都变化的力.
(2)处理方法:把这三个力平移到一个矢量三角 ( http: / / www.21cnjy.com )形中,找到题目情景中的结构三角形,这时往往三个力组成的力三角形与此结构三角形相似.利用三角形的相似比判断出这两个变力大小的变化情况.
例2 如图3所示,一个光滑的小球,放置在墙壁和斜木板之间,当斜木板和竖直墙壁的夹角θ角缓慢增大时(θ<90°),则( )
( http: / / www.21cnjy.com )
图3
A.墙壁受到的压力减小,木板受到的压力减小
B.墙壁受到的压力增大,木板受到的压力减小
C.墙壁受到的压力增大,木板受到的压力增大
D.墙壁受到的压力减小,木板受到的压力增大
解析 以小球为研究对象,处 ( http: / / www.21cnjy.com )于平衡状态,根据受力平衡,有:由图可知,墙壁给球的压力F2逐渐减小,斜木板给球的支持力F1逐渐减小,根据牛顿第三定律可知墙壁受到的压力减小,木板受到的压力减小,故B、C错误,A正确.
( http: / / www.21cnjy.com )
答案 A
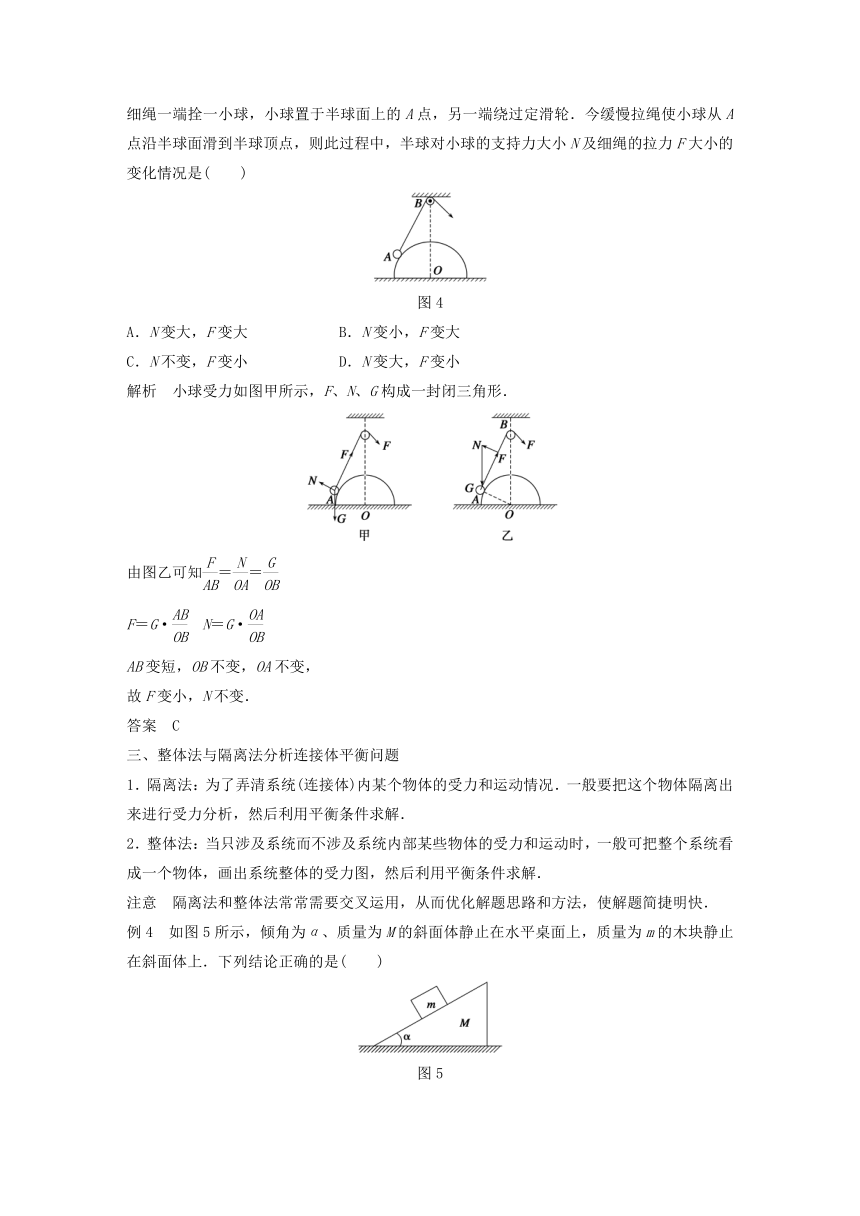
例3 如图4所示,固定在水平面上的光滑半球,球心O的正上方固定一个光滑小定滑轮,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮.今缓慢拉绳使小球从A点沿半球面滑到半球顶点,则此过程中,半球对小球的支持力大小N及细绳的拉力F大小的变化情况是( )
( http: / / www.21cnjy.com )
图4
A.N变大,F变大 B.N变小,F变大
C.N不变,F变小 D.N变大,F变小
解析 小球受力如图甲所示,F、N、G构成一封闭三角形.
( http: / / www.21cnjy.com )
由图乙可知==
F=G· N=G·
AB变短,OB不变,OA不变,
故F变小,N不变.
答案 C
三、整体法与隔离法分析连接体平衡问题
1.隔离法:为了弄清系统(连接体)内某个物体的受力和运动情况.一般要把这个物体隔离出来进行受力分析,然后利用平衡条件求解.
2.整体法:当只涉及系统而不涉及系统内部某些物体的受力和运动时,一般可把整个系统看成一个物体,画出系统整体的受力图,然后利用平衡条件求解.
注意 隔离法和整体法常常需要交叉运用,从而优化解题思路和方法,使解题简捷明快.
例4 如图5所示,倾角为α、质量为M的斜面体静止在水平桌面上,质量为m的木块静止在斜面体上.下列结论正确的是( )
( http: / / www.21cnjy.com )
图5
A.木块受到的摩擦力大小是mgcos α
B.木块对斜面体的压力大小是mgsin α
C.桌面对斜面体的摩擦力大小是mgsin αcos α
D.桌面对斜面体的支持力大小是(M+m)g
解析 先选木块和斜面整体 ( http: / / www.21cnjy.com )为研究对象,由于两者都处于平衡状态,故斜面不受到地面的摩擦力,且地面对斜面体的支持力等于总重力,C项错误,D项正确;再选木块为研究对象,木块受到重力、支持力和斜面对它的滑动摩擦力,木块的重力平行于斜面方向的分力为mgsin α,垂直于斜面方向的分力为mgcos α.由平衡条件可得木块受到的摩擦力大小是f= mgsin α,支持力N=mgcos α,由牛顿第三定律,木块对斜面体的压力大小是mgcos α,选项A、B错误.
答案 D
1.矢量三角形法 合成法 .
2.动态平衡问题: 1 图解法; 2 相似三角形法.
3.整体法与隔离法分析连接体平衡问题.
( http: / / www.21cnjy.com )1.(矢量三角形法)用三根轻绳将质量为m的物块悬挂在空中,如图6所示.已知ac和bc与竖直方向的夹角分别为30°和60°,则ac绳和bc绳中的拉力分别为( )
( http: / / www.21cnjy.com )
图6
A.mg,mg
B.mg,mg
C.mg,mg
D.mg,mg
答案 A
( http: / / www.21cnjy.com )
解析 分析结点c的受力情况如图,设ac ( http: / / www.21cnjy.com )绳受到的拉力为F1、bc绳受到的拉力为F2,根据平衡条件知F1、F2的合力F与重力mg等大、反向,由几何知识得
F1=Fcos 30°=mg
F2=Fsin 30°=mg
选项A正确.
2.(动态平衡问题)用细绳OA、OB悬 ( http: / / www.21cnjy.com )挂一重物,OB水平,O为半圆形支架的圆心,悬点A和B在支架上.悬点A固定不动,将悬点B从图7所示位置逐渐移到C点的过程中,试分析OA绳和OB绳中的拉力变化情况为( )
( http: / / www.21cnjy.com )
图7
A.OA绳中的拉力逐渐减小
B.OA绳中的拉力逐渐增大
C.OB绳中的拉力逐渐减小
D.OB绳中的拉力先减小后增大
答案 AD
( http: / / www.21cnjy.com )
解析 如图所示,在支架上选取三个点 ( http: / / www.21cnjy.com )B1、B2、B3,当悬点B分别移动到B1、B2、B3各点时,OA、OB中的拉力分别为TA1、TA2、TA3和TB1、TB2、TB3,从图中可以直观地看出,TA逐渐变小,且方向不变;而TB先变小后变大,且方向不断改变;当TB与TA垂直时,TB最小,然后TB又逐渐增大.故A、D正确.
3.(整体法与隔离法)如图8所示,质量分 ( http: / / www.21cnjy.com )别为m1、m2的两个物体通过轻弹簧连接,在力F的作用下一起沿水平方向做匀速直线运动(m1在地面上,m2在空中),力F与水平方向成θ角.则m1所受支持力N和摩擦力f正确的是( )
( http: / / www.21cnjy.com )
图8
A.N=m1g+m2g-Fsin θ
B.N=m1g+m2g-Fcos θ
C.f=Fcos θ
D.f=Fsin θ
答案 AC
解析 将m1、m2和弹簧看做一个整体,受力分析如图所示.
( http: / / www.21cnjy.com )
根据平衡条件得f=Fcos θ
N+Fsin θ=(m1+m2)g
则N=(m1+m2)g-Fsin θ
故选项A、C正确.
4.(矢量三角形法)如图9所示,电灯 ( http: / / www.21cnjy.com )的重力为20 N,绳AO与天花板间的夹角为45°,绳BO水平,求绳AO、BO上的拉力的大小.(请分别用两种方法求解)
( http: / / www.21cnjy.com )
图9
答案 20 N 20 N
解析 解法一 矢量三角形法(力的合成法)
O点受三个力作用处于平衡状态,如图所示,
( http: / / www.21cnjy.com )
可得出FA与FB的合力F合方向竖直向上,大小等于FC.
由三角函数关系可得
F合=FAsin 45°=FC=G灯
FB=FAcos 45°
解得FA=20 N,FB=20 N
故绳AO、BO上的拉力分别为20 N、20 N.
解法二 正交分解法
如图所示,将FA进行正交分解,根据物体的平衡条件知
( http: / / www.21cnjy.com )
FAsin 45°=FC
FAcos 45°=FB
FC=G灯
代入数据解得:FA=20 N,FB=20 N.
( http: / / www.21cnjy.com )
题组一 动态平衡问题
1.如图1,电灯悬挂于两墙之间,更换水平绳OA使连结点A向上移动而保持O点的位置不变,则A点向上移动时( )
( http: / / www.21cnjy.com )
图1
A.绳OA的拉力逐渐增大
B.绳OA的拉力逐渐减小
C.绳OA的拉力先增大后减小
D.绳OA的拉力先减小后增大
答案 D
解析 对点O受力分析,如图所示,通过作图,可以看出绳OA的张力先变小后变大,故A、B、C错误,D正确.
( http: / / www.21cnjy.com )
2.用细绳将重球悬挂在竖直光滑墙上如图2所示,当悬挂绳变长时( )
图2
A.绳子拉力变小,墙对球的弹力变大
B.绳子拉力变小,墙对球的弹力变小
C.绳子拉力变大,墙对球的弹力变大
D.绳子拉力变大,墙对球的弹力变小
答案 B
解析 对小球进行受力分析:把绳子的拉力T和墙对球的弹力N合成F,由于物体是静止的,所以物体受力平衡,所以物体的重力等于合力F,即F=G,
设细线与墙壁的夹角为θ,根据几何关系得 ( http: / / www.21cnjy.com )出:T=,N=mgtan θ,先找到其中的定值,就是小球的重力mg,mg是不变的,随着绳子加长,细线与墙壁的夹角θ减小,则cos θ增大,减小,tan θ减小,mgtan θ减小,所以,T减小,N减小.故选B.
3.一轻杆BO,其O端用光滑铰 ( http: / / www.21cnjy.com )链铰于固定竖直杆AO上,B端挂一重物,且系一细绳,细绳跨过杆顶A处的光滑小滑轮,用力F拉住,如图3所示.现将细绳缓慢往左拉,使轻杆BO与杆AO间的夹角θ逐渐减小,则在此过程中,拉力F及轻杆BO对绳的支持力N的大小变化情况是( )
( http: / / www.21cnjy.com )
图3
A.N先减小,后增大
B.N始终不变
C.F先减小,后增大
D.F始终不变
答案 B
解析 取BO杆的B端为研究对象,受到绳 ( http: / / www.21cnjy.com )子拉力(大小为F)、BO杆的支持力N和悬挂重物的绳子的拉力(大小为G),如图所示,得到一个力三角形(如图中画斜线部分),此力三角形与几何三角形OBA相似,可利用相似三角形对应边成比例来解.
( http: / / www.21cnjy.com )
如图所示,力三角形与几何三角形OBA相似,设AO高为H,BO长为L,绳长为l,则由对应边成比例可得:
==
式中G、H、L均不变,l逐渐变小,所以可知N不变,F逐渐变小.故选B.
4.如图4所示,用细绳悬挂一个小球,小球在 ( http: / / www.21cnjy.com )水平拉力F的作用下从平衡位置P点缓慢地沿圆弧移动到Q点,在这个过程中,绳的拉力F′和水平拉力F的大小变化情况是( )
( http: / / www.21cnjy.com )
图4
A.F′不断增大
B.F′不断减小
C.F不断减小
D.F不断增大
答案 AD
解析 如图所示,利用图解法可知F′不断增大,F不断增大.
( http: / / www.21cnjy.com )
5.置于水平地面上的物体受到 ( http: / / www.21cnjy.com )水平作用力F处于静止状态,如图5所示,保持作用力F大小不变,将其沿逆时针方向缓缓转过180°,物体始终保持静止,则在此过程中地面对物体的支持力N和地面给物体的摩擦力f的变化情况是( )
图5
A.N先变小后变大,f不变
B.N不变,f先变小后变大
C.N、f都是先变大后变小
D.N、f都是先变小后变大
答案 D
解析 力F与水平方向的夹角θ先增大后减 ( http: / / www.21cnjy.com )小,水平方向上,Fcos θ-f=0,f=Fcos θ;竖直方向上,N+Fsin θ-mg=0,N=mg-Fsin θ,故随θ变化,f、N都是先减小后增大.
题组二 整体法与隔离法
6.两刚性球a和b的质量分别为ma和m ( http: / / www.21cnjy.com )b、直径分别为da和db(da>db)将a、b球依次放入一竖直放置、平底的圆筒内,如图6所示.设a、b两球静止时圆筒侧面对两球的弹力大小分别为F1和F2,筒底对球a的支持力大小为F.已知重力加速度大小为g.若所有接触都是光滑的,则( )
( http: / / www.21cnjy.com )
图6
A.F=(ma+mb)g F1=F2
B.F=(ma+mb)g F1≠F2
C.mag<F<(ma+mb)g
D.mag<F<(ma+mb)g,F1≠F2
答案 A
解析 对两刚性球a和b整体受力分析,由竖直方向受力平衡可知F=(ma+mb)g、水平方向受力平衡有F1=F2.
7.如图7所示,测力计、绳子和滑轮的质量都不计,摩擦力不计.物体A重40 N,物体B重10 N,以下说法正确的是( )
( http: / / www.21cnjy.com )
图7
A.地面对A的支持力是30 N
B.物体A受到的合力是30 N
C.测力计示数20 N
D.测力计示数30 N
答案 AC
8.在粗糙水平面上放着一个质量为M的三角 ( http: / / www.21cnjy.com )形木块abc,在它的两个粗糙斜面上分别放有质量为m1和m2的两个物体,m1>m2,如图8所示,若三角形木块和两物体都是静止的,则粗糙水平面对三角形木块( )
图8
A.无摩擦力的作用
B.有摩擦力的作用,摩擦力的方向水平向左
C.有摩擦力的作用,但摩擦力的方向不能确定,因m1、m2、θ1、θ2的数值均未给出
D.地面对三角形木块的支持力大小为(m1+m2+M)g
答案 AD
( http: / / www.21cnjy.com )
解析 由于三角形木块和斜面上的两物体都静止, ( http: / / www.21cnjy.com )可以把它们看成一个整体,如图所示,整体竖直方向受到重力(m1+m2+M)g和支持力N作用处于平衡状态,故地面对整体的支持力大小为(m1+m2+M)g,故D选项正确.水平方向无任何滑动趋势,因此不受地面的摩擦力作用.故A选项正确.
9.如图9所示,在粗糙水平地面上放着 ( http: / / www.21cnjy.com )一个截面为四分之一圆弧的柱状物体A,A的左端紧靠竖直墙,A与竖直墙壁之间放一光滑球B,整个装置处于静止状态.若把A向右移动少许后,它们仍处于静止状态,则( )
( http: / / www.21cnjy.com )
图9
A.B对墙的压力减小
B.A与B之间的作用力增大
C.地面对A的摩擦力减小
D.A对地面的压力不变
答案 ACD
解析 设物体A对球B的支持力为F1,竖 ( http: / / www.21cnjy.com )直墙对球B的弹力为F2,F1与竖直方向的夹角θ因物体A右移而减小.对球B受力分析如图所示,由平衡条件得:F1cos θ=mBg,F1sin θ=F2,解得F1=,F2=mBgtan θ, θ减小,F1减小,F2减小,选项A对,B错;对A、B整体受力分析可知,竖直方向,地面对整体的支持力N=(mA+mB)g,与θ无关,即A对地面的压力不变,选项D对;水平方向,地面对A的摩擦力f=F2,因F2减小,故f减小,选项C对.
( http: / / www.21cnjy.com )
题组三 矢量三角形法求解共点力的平衡问题
10.一个物体受到三个力的作用,三力构成的矢量图如图所示,则能够使物体处于平衡状态的是( )
( http: / / www.21cnjy.com )
答案 A
11.如图10所示,两根等长的轻绳将日光灯悬挂在天花板上,两绳与竖直方向的夹角都为45°,日光灯保持水平,所受重力为G.则( )
( http: / / www.21cnjy.com )
图10
A.两绳对日光灯拉力的合力大小为G
B.两绳的拉力和重力不是共点力
C.两绳的拉力大小分别为G和G
D.两绳的拉力大小分别为和
答案 AC
解析 如图,
( http: / / www.21cnjy.com )
两绳拉力的作用线与重力作用线的延长线交于 ( http: / / www.21cnjy.com )一点,这三个力为共点力,B选项错误;由于日光灯在两绳拉力和重力作用下处于静止状态,所以两绳的拉力的合力与重力G等大反向,A选项正确;由于两个拉力的夹角成直角,且都与竖直方向成45°角,则由力的平行四边形定则可知G=,F1=F2,故F1=F2=G,C选项正确,D选项错误.
12.如图11所示,一个重为100 ( http: / / www.21cnjy.com ) N、质量分布均匀的小球被夹在竖直的墙壁和A点之间,已知球心O与A点的连线与竖直方向成θ角,且θ=60°,所有接触点和面均不计摩擦.试求墙面对小球的支持力F1和A点对小球的压力F2.
( http: / / www.21cnjy.com )
图11
答案 100 N,方向垂直墙壁向左 200 N,方向由A指向O
解析 如图,
( http: / / www.21cnjy.com )
小球受重力mg、竖直墙面对球的弹力F1和A点对球的弹力F2作用.由三力平衡条件知F1与F2的合力与mg等大反向,解直角三角形得
F1=mgtan θ=100 N,方向垂直墙壁向左
F2==200 N,方向由A指向O
13.滑板运动是一项非常刺激的水上运 ( http: / / www.21cnjy.com )动.研究表明,在进行滑板运动时,水对滑板的作用力N垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时(如图12),滑板做匀速直线运动,相应的k=54 kg/m,人和滑板的总质量为108 kg,试求:(重力加速度g取10 m/s2,sin 37°取,忽略空气阻力)
图12
(1)水平牵引力的大小;
(2)滑板的速率.
答案 (1)810 N (2)5 m/s
解析 (1)以滑板和运动员整体为研究对象,其受力如图所示(三力组成矢量三角形)
( http: / / www.21cnjy.com )
由共点力平衡条件可得
Ncos θ=mg①
Nsin θ=F②
联立①②得
F=810 N
(2)N=
N=kv2
解得v= =5 m/s
[目标定位]
1.进一步理解共点力作用下物体的平衡条件.
2.掌握矢量三角形法解共点力作用下的平衡问题.3.掌握动态平衡问题的分析方法.4.掌握整体法和隔离法分析连接体平衡问题.
( http: / / www.21cnjy.com )
一、矢量三角形法(合成法)求解共点力平衡问题
物体受多力作用处于平衡状态时,可用正交分 ( http: / / www.21cnjy.com )解法求解,但当物体受三个力作用而平衡时,可用矢量三角形法,即其中任意两个力的合力与第三个力大小相等、方向相反,且这三个力首尾相接构成封闭三角形,通过解三角形求解相应力的大小和方向,当这三个力组成含有特殊角(60°、53°、45°)的直角三角形时尤为简单.
例1 在科学研究中,可以用风力仪直接测量风力的大小,其原理如图1所示.仪器中一根轻质金属丝,悬挂着一个金属球.无风时,金属丝竖直下垂;当受到沿水平方向吹来的风时,金属丝偏离竖直方向一个角度.风力越大,偏角越大,通过传感器,就可以根据偏角的大小指示出风力的大小,那么风力大小F跟金属球的质量m、偏角θ之间有什么样的关系呢?(试用矢量三角形法和正交分解法两种方法求解)
( http: / / www.21cnjy.com )
图1
解析 取金属球为研究对象,有风时,它受到三 ( http: / / www.21cnjy.com )个力的作用:重力mg、水平方向的风力F和金属丝的拉力T,如图甲所示.这三个力是共点力,在这三个共点力的作用下金属球处于平衡状态,则这三个力的合力为零,可以根据任意两力的合力与第三个力等大、反向求解,也可以用正交分解法求解.
( http: / / www.21cnjy.com )
甲
解法一 矢量三角形法
如图乙所示,风力F和拉力T的合力与重力等大反向,由矢量三角形可得:F=mgtan θ.
( http: / / www.21cnjy.com )
解法二 正交分解法
以金属球为坐标原点,取水平方向为x轴,竖直 ( http: / / www.21cnjy.com )方向为y轴,建立直角坐标系,如图丙所示.有水平方向的合力Fx合和竖直方向的合力Fy合分别等于零,即
Fx合=Tsin θ-F=0,Fy合=Tcos θ-mg=0,
解得F=mgtan θ.由所得结果可见,当金属球的质量m一定时,风力F只跟偏角θ有关.因此,根据偏角θ的大小就可以指示出风力的大小.
答案 F=mgtan θ
针对训练 如图2所示,光滑 ( http: / / www.21cnjy.com )半球形容器固定在水平面上,O为球心,一质量为m的小滑块,在水平力F的作用下静止于P点,设滑块所受支持力为N,OP与水平方向的夹角为θ,下列关系正确的是( )
图2
A.F= B.F=mgtan θ
C.N= D.N=mgtan θ
答案 A
解析 对滑块进行受力分析如图,滑块受到 ( http: / / www.21cnjy.com )重力mg、支持力N、水平推力F三个力作用.由共点力的平衡条件知,F与mg的合力F′与N等大、反向.根据平行四边形定则可知N、mg和合力F′构成直角三角形,解直角三角形可求得:F=,N=.所以正确选项为A.
( http: / / www.21cnjy.com )
二、动态平衡问题
所谓动态平衡问题是指通过控制某些物 ( http: / / www.21cnjy.com )理量,使物体的状态发生缓慢变化,而在这个过程中物体又始终处于一系列的平衡状态,这类问题的解决方法一般用图解法和相似三角形法.
1.图解法
(1)特征:物体受三个力作用,这三 ( http: / / www.21cnjy.com )个力中,一个是恒力,大小、方向均不变化,另两个是变力,其中一个是方向不变的力,另一个是大小、方向均变化的力.
(2)处理方法:把这三个力平移到一个矢量三角形中,利用图解法判断两个变力大小、方向的变化.
2.相似三角形法
(1)特征:物体一般也受三个力作用,这三个力中,一个是恒力,另两个是大小、方向都变化的力.
(2)处理方法:把这三个力平移到一个矢量三角 ( http: / / www.21cnjy.com )形中,找到题目情景中的结构三角形,这时往往三个力组成的力三角形与此结构三角形相似.利用三角形的相似比判断出这两个变力大小的变化情况.
例2 如图3所示,一个光滑的小球,放置在墙壁和斜木板之间,当斜木板和竖直墙壁的夹角θ角缓慢增大时(θ<90°),则( )
( http: / / www.21cnjy.com )
图3
A.墙壁受到的压力减小,木板受到的压力减小
B.墙壁受到的压力增大,木板受到的压力减小
C.墙壁受到的压力增大,木板受到的压力增大
D.墙壁受到的压力减小,木板受到的压力增大
解析 以小球为研究对象,处 ( http: / / www.21cnjy.com )于平衡状态,根据受力平衡,有:由图可知,墙壁给球的压力F2逐渐减小,斜木板给球的支持力F1逐渐减小,根据牛顿第三定律可知墙壁受到的压力减小,木板受到的压力减小,故B、C错误,A正确.
( http: / / www.21cnjy.com )
答案 A
例3 如图4所示,固定在水平面上的光滑半球,球心O的正上方固定一个光滑小定滑轮,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮.今缓慢拉绳使小球从A点沿半球面滑到半球顶点,则此过程中,半球对小球的支持力大小N及细绳的拉力F大小的变化情况是( )
( http: / / www.21cnjy.com )
图4
A.N变大,F变大 B.N变小,F变大
C.N不变,F变小 D.N变大,F变小
解析 小球受力如图甲所示,F、N、G构成一封闭三角形.
( http: / / www.21cnjy.com )
由图乙可知==
F=G· N=G·
AB变短,OB不变,OA不变,
故F变小,N不变.
答案 C
三、整体法与隔离法分析连接体平衡问题
1.隔离法:为了弄清系统(连接体)内某个物体的受力和运动情况.一般要把这个物体隔离出来进行受力分析,然后利用平衡条件求解.
2.整体法:当只涉及系统而不涉及系统内部某些物体的受力和运动时,一般可把整个系统看成一个物体,画出系统整体的受力图,然后利用平衡条件求解.
注意 隔离法和整体法常常需要交叉运用,从而优化解题思路和方法,使解题简捷明快.
例4 如图5所示,倾角为α、质量为M的斜面体静止在水平桌面上,质量为m的木块静止在斜面体上.下列结论正确的是( )
( http: / / www.21cnjy.com )
图5
A.木块受到的摩擦力大小是mgcos α
B.木块对斜面体的压力大小是mgsin α
C.桌面对斜面体的摩擦力大小是mgsin αcos α
D.桌面对斜面体的支持力大小是(M+m)g
解析 先选木块和斜面整体 ( http: / / www.21cnjy.com )为研究对象,由于两者都处于平衡状态,故斜面不受到地面的摩擦力,且地面对斜面体的支持力等于总重力,C项错误,D项正确;再选木块为研究对象,木块受到重力、支持力和斜面对它的滑动摩擦力,木块的重力平行于斜面方向的分力为mgsin α,垂直于斜面方向的分力为mgcos α.由平衡条件可得木块受到的摩擦力大小是f= mgsin α,支持力N=mgcos α,由牛顿第三定律,木块对斜面体的压力大小是mgcos α,选项A、B错误.
答案 D
1.矢量三角形法 合成法 .
2.动态平衡问题: 1 图解法; 2 相似三角形法.
3.整体法与隔离法分析连接体平衡问题.
( http: / / www.21cnjy.com )1.(矢量三角形法)用三根轻绳将质量为m的物块悬挂在空中,如图6所示.已知ac和bc与竖直方向的夹角分别为30°和60°,则ac绳和bc绳中的拉力分别为( )
( http: / / www.21cnjy.com )
图6
A.mg,mg
B.mg,mg
C.mg,mg
D.mg,mg
答案 A
( http: / / www.21cnjy.com )
解析 分析结点c的受力情况如图,设ac ( http: / / www.21cnjy.com )绳受到的拉力为F1、bc绳受到的拉力为F2,根据平衡条件知F1、F2的合力F与重力mg等大、反向,由几何知识得
F1=Fcos 30°=mg
F2=Fsin 30°=mg
选项A正确.
2.(动态平衡问题)用细绳OA、OB悬 ( http: / / www.21cnjy.com )挂一重物,OB水平,O为半圆形支架的圆心,悬点A和B在支架上.悬点A固定不动,将悬点B从图7所示位置逐渐移到C点的过程中,试分析OA绳和OB绳中的拉力变化情况为( )
( http: / / www.21cnjy.com )
图7
A.OA绳中的拉力逐渐减小
B.OA绳中的拉力逐渐增大
C.OB绳中的拉力逐渐减小
D.OB绳中的拉力先减小后增大
答案 AD
( http: / / www.21cnjy.com )
解析 如图所示,在支架上选取三个点 ( http: / / www.21cnjy.com )B1、B2、B3,当悬点B分别移动到B1、B2、B3各点时,OA、OB中的拉力分别为TA1、TA2、TA3和TB1、TB2、TB3,从图中可以直观地看出,TA逐渐变小,且方向不变;而TB先变小后变大,且方向不断改变;当TB与TA垂直时,TB最小,然后TB又逐渐增大.故A、D正确.
3.(整体法与隔离法)如图8所示,质量分 ( http: / / www.21cnjy.com )别为m1、m2的两个物体通过轻弹簧连接,在力F的作用下一起沿水平方向做匀速直线运动(m1在地面上,m2在空中),力F与水平方向成θ角.则m1所受支持力N和摩擦力f正确的是( )
( http: / / www.21cnjy.com )
图8
A.N=m1g+m2g-Fsin θ
B.N=m1g+m2g-Fcos θ
C.f=Fcos θ
D.f=Fsin θ
答案 AC
解析 将m1、m2和弹簧看做一个整体,受力分析如图所示.
( http: / / www.21cnjy.com )
根据平衡条件得f=Fcos θ
N+Fsin θ=(m1+m2)g
则N=(m1+m2)g-Fsin θ
故选项A、C正确.
4.(矢量三角形法)如图9所示,电灯 ( http: / / www.21cnjy.com )的重力为20 N,绳AO与天花板间的夹角为45°,绳BO水平,求绳AO、BO上的拉力的大小.(请分别用两种方法求解)
( http: / / www.21cnjy.com )
图9
答案 20 N 20 N
解析 解法一 矢量三角形法(力的合成法)
O点受三个力作用处于平衡状态,如图所示,
( http: / / www.21cnjy.com )
可得出FA与FB的合力F合方向竖直向上,大小等于FC.
由三角函数关系可得
F合=FAsin 45°=FC=G灯
FB=FAcos 45°
解得FA=20 N,FB=20 N
故绳AO、BO上的拉力分别为20 N、20 N.
解法二 正交分解法
如图所示,将FA进行正交分解,根据物体的平衡条件知
( http: / / www.21cnjy.com )
FAsin 45°=FC
FAcos 45°=FB
FC=G灯
代入数据解得:FA=20 N,FB=20 N.
( http: / / www.21cnjy.com )
题组一 动态平衡问题
1.如图1,电灯悬挂于两墙之间,更换水平绳OA使连结点A向上移动而保持O点的位置不变,则A点向上移动时( )
( http: / / www.21cnjy.com )
图1
A.绳OA的拉力逐渐增大
B.绳OA的拉力逐渐减小
C.绳OA的拉力先增大后减小
D.绳OA的拉力先减小后增大
答案 D
解析 对点O受力分析,如图所示,通过作图,可以看出绳OA的张力先变小后变大,故A、B、C错误,D正确.
( http: / / www.21cnjy.com )
2.用细绳将重球悬挂在竖直光滑墙上如图2所示,当悬挂绳变长时( )
图2
A.绳子拉力变小,墙对球的弹力变大
B.绳子拉力变小,墙对球的弹力变小
C.绳子拉力变大,墙对球的弹力变大
D.绳子拉力变大,墙对球的弹力变小
答案 B
解析 对小球进行受力分析:把绳子的拉力T和墙对球的弹力N合成F,由于物体是静止的,所以物体受力平衡,所以物体的重力等于合力F,即F=G,
设细线与墙壁的夹角为θ,根据几何关系得 ( http: / / www.21cnjy.com )出:T=,N=mgtan θ,先找到其中的定值,就是小球的重力mg,mg是不变的,随着绳子加长,细线与墙壁的夹角θ减小,则cos θ增大,减小,tan θ减小,mgtan θ减小,所以,T减小,N减小.故选B.
3.一轻杆BO,其O端用光滑铰 ( http: / / www.21cnjy.com )链铰于固定竖直杆AO上,B端挂一重物,且系一细绳,细绳跨过杆顶A处的光滑小滑轮,用力F拉住,如图3所示.现将细绳缓慢往左拉,使轻杆BO与杆AO间的夹角θ逐渐减小,则在此过程中,拉力F及轻杆BO对绳的支持力N的大小变化情况是( )
( http: / / www.21cnjy.com )
图3
A.N先减小,后增大
B.N始终不变
C.F先减小,后增大
D.F始终不变
答案 B
解析 取BO杆的B端为研究对象,受到绳 ( http: / / www.21cnjy.com )子拉力(大小为F)、BO杆的支持力N和悬挂重物的绳子的拉力(大小为G),如图所示,得到一个力三角形(如图中画斜线部分),此力三角形与几何三角形OBA相似,可利用相似三角形对应边成比例来解.
( http: / / www.21cnjy.com )
如图所示,力三角形与几何三角形OBA相似,设AO高为H,BO长为L,绳长为l,则由对应边成比例可得:
==
式中G、H、L均不变,l逐渐变小,所以可知N不变,F逐渐变小.故选B.
4.如图4所示,用细绳悬挂一个小球,小球在 ( http: / / www.21cnjy.com )水平拉力F的作用下从平衡位置P点缓慢地沿圆弧移动到Q点,在这个过程中,绳的拉力F′和水平拉力F的大小变化情况是( )
( http: / / www.21cnjy.com )
图4
A.F′不断增大
B.F′不断减小
C.F不断减小
D.F不断增大
答案 AD
解析 如图所示,利用图解法可知F′不断增大,F不断增大.
( http: / / www.21cnjy.com )
5.置于水平地面上的物体受到 ( http: / / www.21cnjy.com )水平作用力F处于静止状态,如图5所示,保持作用力F大小不变,将其沿逆时针方向缓缓转过180°,物体始终保持静止,则在此过程中地面对物体的支持力N和地面给物体的摩擦力f的变化情况是( )
图5
A.N先变小后变大,f不变
B.N不变,f先变小后变大
C.N、f都是先变大后变小
D.N、f都是先变小后变大
答案 D
解析 力F与水平方向的夹角θ先增大后减 ( http: / / www.21cnjy.com )小,水平方向上,Fcos θ-f=0,f=Fcos θ;竖直方向上,N+Fsin θ-mg=0,N=mg-Fsin θ,故随θ变化,f、N都是先减小后增大.
题组二 整体法与隔离法
6.两刚性球a和b的质量分别为ma和m ( http: / / www.21cnjy.com )b、直径分别为da和db(da>db)将a、b球依次放入一竖直放置、平底的圆筒内,如图6所示.设a、b两球静止时圆筒侧面对两球的弹力大小分别为F1和F2,筒底对球a的支持力大小为F.已知重力加速度大小为g.若所有接触都是光滑的,则( )
( http: / / www.21cnjy.com )
图6
A.F=(ma+mb)g F1=F2
B.F=(ma+mb)g F1≠F2
C.mag<F<(ma+mb)g
D.mag<F<(ma+mb)g,F1≠F2
答案 A
解析 对两刚性球a和b整体受力分析,由竖直方向受力平衡可知F=(ma+mb)g、水平方向受力平衡有F1=F2.
7.如图7所示,测力计、绳子和滑轮的质量都不计,摩擦力不计.物体A重40 N,物体B重10 N,以下说法正确的是( )
( http: / / www.21cnjy.com )
图7
A.地面对A的支持力是30 N
B.物体A受到的合力是30 N
C.测力计示数20 N
D.测力计示数30 N
答案 AC
8.在粗糙水平面上放着一个质量为M的三角 ( http: / / www.21cnjy.com )形木块abc,在它的两个粗糙斜面上分别放有质量为m1和m2的两个物体,m1>m2,如图8所示,若三角形木块和两物体都是静止的,则粗糙水平面对三角形木块( )
图8
A.无摩擦力的作用
B.有摩擦力的作用,摩擦力的方向水平向左
C.有摩擦力的作用,但摩擦力的方向不能确定,因m1、m2、θ1、θ2的数值均未给出
D.地面对三角形木块的支持力大小为(m1+m2+M)g
答案 AD
( http: / / www.21cnjy.com )
解析 由于三角形木块和斜面上的两物体都静止, ( http: / / www.21cnjy.com )可以把它们看成一个整体,如图所示,整体竖直方向受到重力(m1+m2+M)g和支持力N作用处于平衡状态,故地面对整体的支持力大小为(m1+m2+M)g,故D选项正确.水平方向无任何滑动趋势,因此不受地面的摩擦力作用.故A选项正确.
9.如图9所示,在粗糙水平地面上放着 ( http: / / www.21cnjy.com )一个截面为四分之一圆弧的柱状物体A,A的左端紧靠竖直墙,A与竖直墙壁之间放一光滑球B,整个装置处于静止状态.若把A向右移动少许后,它们仍处于静止状态,则( )
( http: / / www.21cnjy.com )
图9
A.B对墙的压力减小
B.A与B之间的作用力增大
C.地面对A的摩擦力减小
D.A对地面的压力不变
答案 ACD
解析 设物体A对球B的支持力为F1,竖 ( http: / / www.21cnjy.com )直墙对球B的弹力为F2,F1与竖直方向的夹角θ因物体A右移而减小.对球B受力分析如图所示,由平衡条件得:F1cos θ=mBg,F1sin θ=F2,解得F1=,F2=mBgtan θ, θ减小,F1减小,F2减小,选项A对,B错;对A、B整体受力分析可知,竖直方向,地面对整体的支持力N=(mA+mB)g,与θ无关,即A对地面的压力不变,选项D对;水平方向,地面对A的摩擦力f=F2,因F2减小,故f减小,选项C对.
( http: / / www.21cnjy.com )
题组三 矢量三角形法求解共点力的平衡问题
10.一个物体受到三个力的作用,三力构成的矢量图如图所示,则能够使物体处于平衡状态的是( )
( http: / / www.21cnjy.com )
答案 A
11.如图10所示,两根等长的轻绳将日光灯悬挂在天花板上,两绳与竖直方向的夹角都为45°,日光灯保持水平,所受重力为G.则( )
( http: / / www.21cnjy.com )
图10
A.两绳对日光灯拉力的合力大小为G
B.两绳的拉力和重力不是共点力
C.两绳的拉力大小分别为G和G
D.两绳的拉力大小分别为和
答案 AC
解析 如图,
( http: / / www.21cnjy.com )
两绳拉力的作用线与重力作用线的延长线交于 ( http: / / www.21cnjy.com )一点,这三个力为共点力,B选项错误;由于日光灯在两绳拉力和重力作用下处于静止状态,所以两绳的拉力的合力与重力G等大反向,A选项正确;由于两个拉力的夹角成直角,且都与竖直方向成45°角,则由力的平行四边形定则可知G=,F1=F2,故F1=F2=G,C选项正确,D选项错误.
12.如图11所示,一个重为100 ( http: / / www.21cnjy.com ) N、质量分布均匀的小球被夹在竖直的墙壁和A点之间,已知球心O与A点的连线与竖直方向成θ角,且θ=60°,所有接触点和面均不计摩擦.试求墙面对小球的支持力F1和A点对小球的压力F2.
( http: / / www.21cnjy.com )
图11
答案 100 N,方向垂直墙壁向左 200 N,方向由A指向O
解析 如图,
( http: / / www.21cnjy.com )
小球受重力mg、竖直墙面对球的弹力F1和A点对球的弹力F2作用.由三力平衡条件知F1与F2的合力与mg等大反向,解直角三角形得
F1=mgtan θ=100 N,方向垂直墙壁向左
F2==200 N,方向由A指向O
13.滑板运动是一项非常刺激的水上运 ( http: / / www.21cnjy.com )动.研究表明,在进行滑板运动时,水对滑板的作用力N垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时(如图12),滑板做匀速直线运动,相应的k=54 kg/m,人和滑板的总质量为108 kg,试求:(重力加速度g取10 m/s2,sin 37°取,忽略空气阻力)
图12
(1)水平牵引力的大小;
(2)滑板的速率.
答案 (1)810 N (2)5 m/s
解析 (1)以滑板和运动员整体为研究对象,其受力如图所示(三力组成矢量三角形)
( http: / / www.21cnjy.com )
由共点力平衡条件可得
Ncos θ=mg①
Nsin θ=F②
联立①②得
F=810 N
(2)N=
N=kv2
解得v= =5 m/s
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
