北京市第一六一中学2023~2024学年九年级下学期开学考数学试题(无答案)
文档属性
| 名称 | 北京市第一六一中学2023~2024学年九年级下学期开学考数学试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 957.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 15:37:19 | ||
图片预览


文档简介
北京一六一中学2023—2024学年度第二学期开学测试
初三数学试卷
2024年2月
班级________________姓名________________学号________________
考生须知 1.本试卷共4页,满分100分,考试时间120分钟。2.试卷答案一律填涂在答题卡或书写在答题纸上,在试卷上作答无效。3.在答题卡上,用2B铅笔作答,在答题纸上,用黑色字迹签字笔作答。4.考试结束后,将答题卡、答题纸一并交回。
一、选择题(本题共16分,每小题2分。在每小题给出的四个选项中,只有一项符合题目的要求。把正确答案涂写在答题纸上相应的位置。)
1.2023年5月30日神舟十六号载人飞船发射取得圆满成功,此次任务是我国载人航天工程进入空间站应用与发展阶段的首次载人飞行任务.下列有关航天的4个图标图案中是中心对称图形的是( )
A. B. C. D.
2.抛物线的顶点坐标是( )
A. B. C. D.
3.将一元二次方程通过配方转化为的形式,下列结果中正确的是( )
A. B. C. D.
4.如图,是的一条弦,直径是,若,垂足为,,,则的长度为( )
A.5 B.6 C.8 D.10
5.实数、、在数轴上对应点的位置如图所示.如果,那么下列结论正确的是( )
A. B. C. D.
5.不透明的袋子中有两个小球,上面分别写着数字“1”,“2”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )
A. B. C. D.
7.根据下列表格中二次函数的自变量与函数值的对应值,判断方程(,,,为常数)的一个解的范围是( )
6.17 6.18 6.19 6.20
0.02 0.04
A. B. C. D.
8.目标完成率,一般是指个体的实际完成量与目标完成量的比值,树立明确具体的目标,能够促使人们更好地完成任务.某读书会有10位成员(编号分别为),如图是根据他们年初制定的目标阅读量和年末实际完成情况绘制的统计图,下列结论正确的有( )
①目标完成率为100%的是,;
②目标阅读量与实际阅读量相差最多的是;
③目标完成率最高的是,最低的是;
④目标完成率超过75%且实际阅读量不少于5本的有三人.
A.①② B.①②③ C.①③④ D.①②③④
二、填空题(本题共8道小题,每小题2分,共16分)
9.因式分解:________.
10.二次函数的图象与轴的交点坐标为________.
11.若点,,在抛物线上,则,,的大小关系为________(用“”连接).
12.如图,将绕点逆时针旋转一定角度,得到,若,,且,则的度数为________.
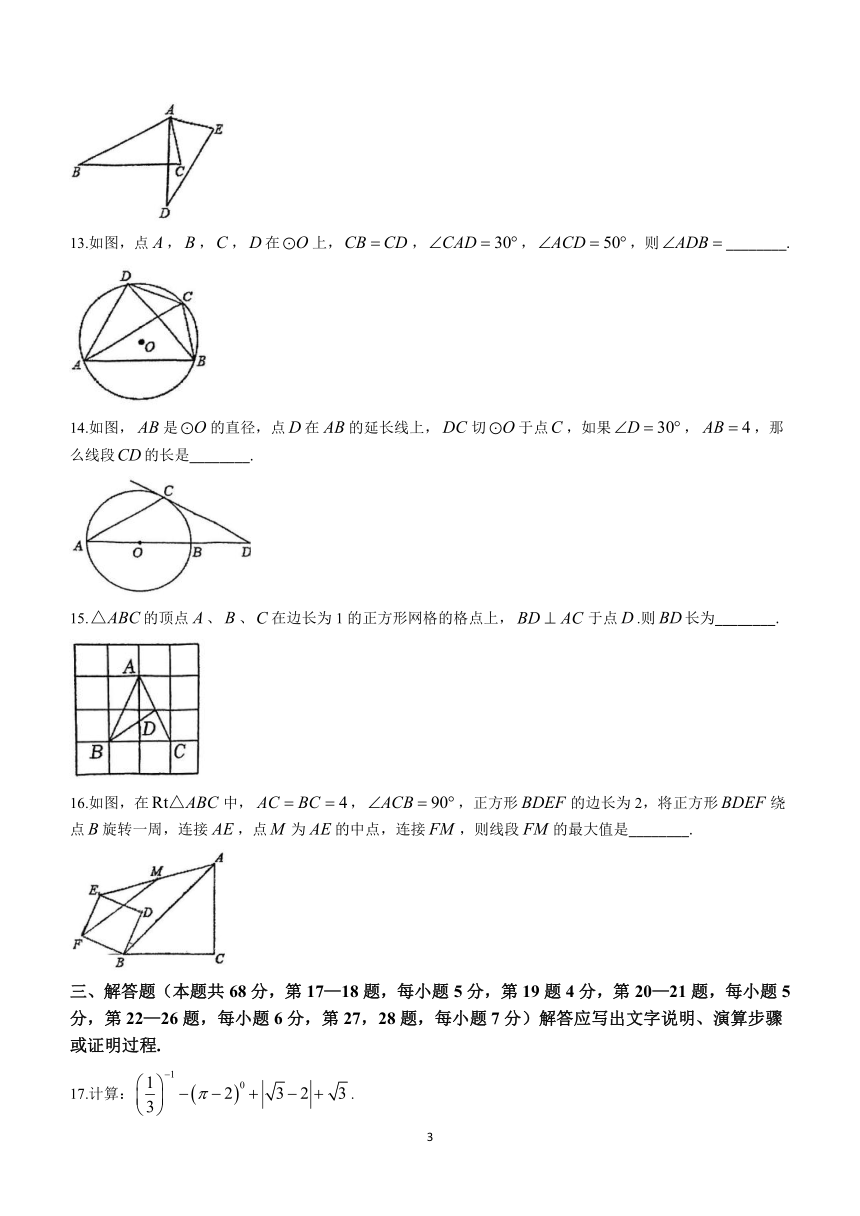
13.如图,点,,,在上,,,,则________.
14.如图,是的直径,点在的延长线上,切于点,如果,,那么线段的长是________.
15.的顶点、、在边长为1的正方形网格的格点上,于点.则长为________.
16.如图,在中,,,正方形的边长为2,将正方形绕点旋转一周,连接,点为的中点,连接,则线段的最大值是________.
三、解答题(本题共68分,第17—18题,每小题5分,第19题4分,第20—21题,每小题5分,第22—26题,每小题6分,第27,28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17.计算:.
18.解不等式组,并写出它的所有非负整数解.
19.阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:为外一点.
求作:经过点的的切线.
小敏的作法如下:
如图,
①连接,作线段的垂直平分线交于点.
②以点为圆心,的长为半径作圆,交于,两点.
③作直线,.
(1)请补充完整小敏的作图;
(2)连接,可证,其依据是________.由此可证明直线,都是的切线,其依据是________.
20.已知,关于的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若该方程有一个根是负数,求的取值范围.
21.如图,在中,,点,,分别为,,的中点.
(1)求证:四边形是菱形;
(2)若,,求四边形的面积.
22.对于拋物线.
(1)它与轴交点的坐标为________,与轴交点的坐标为________,顶点坐标为________;
(2)在坐标系中利用描点法画出此抛物线;
(3)当时,结合函数图象,直接写出的取值范围________;
(4)若点,在抛物线上,且,直接写出的取值范围________.
23.在平面直角坐标系中,直线与轴交于点,直线:经过点,且与轴交于点.
(1)求点和点的坐标及直线的解析式;
(2)直线与直线关于直线对称,若直线与直线,围成的区域内(不包含边界)恰有1个整点,直接写出的取值范围.(注:横、纵坐标都是整数的点叫做整点.)
24.如图,在中,,为的直径,与相交于点,过点作于点,延长线交于点.
(1)求证:为的切线;
(2)若,,求的长.
25.通常把脏衣服用洗衣液清洗后会进行拧干,但由于不可能拧净衣服上的全部污水,所以还需要用清水进行多次漂洗,不断降低衣服中污水的含量.某小组研究了如何用清水漂洗衣服效果更好,部分内容如下,请补充完整:实验研究:先准备几件相同的洗过一次并拧干(存留一些污水)的衣服,把每件衣服分别用一定量的清水浸泡,经过充分搓洗,使清水与衣服上存留的污水混合均匀,然后拧干,视为一次漂洗,称重、记录每次漂洗后衣服上存留的污水重量和比例,如:把一件存留1斤污水的衣服用10斤清水漂洗后,拧干到仍然存留1斤污水,则漂洗后衣服中存有的污物是原来的,在多次实验后,通过对收集的数据进行分析,该小组决定使用20斤清水,采用三种不同的方案,对每件衣服分别进行漂洗,并假设每次拧干后的衣服上都存留约1斤的污水.
数据计算:对三种漂洗方案进行计算、比较.
方案一:采用一次漂洗的方式.将20斤清水一次用掉,漂洗后衣服中存有的污物是原来的________;
方案二:采用两次漂洗的方式,且两次用水量不同.如第一次用12斤清水,第二次用8斤清水,漂洗后衣服中存有的污物是原来的________;
方案三:采用两次漂洗的方式,且两次用水量相同,每次用10斤清水,漂洗后衣服中存有的污物是原来的________.
实验结论:对比可知,在这三种方案中,方案________的漂洗效果最好(填“一”“二”或“三”).
推广证明:将脏衣服用洗衣液清洗后,再用清水进行漂洗,假设每次拧干后还存留()斤污水,现用()斤清水漂洗(方案二中第一次用水量为斤),请比较并证明方案二与方案三的漂洗效果。
26.在平面直角坐标系中,点,在抛物线上,设抛物线的对称轴为.
(1)当时,求抛物线与轴交点的坐标及的值;
(2)点在抛物线上,若,求的取值范围及的取值范围.
27.已知,点为中点,,为边,上的动点,且满足,为平面内一点,,,连结,.
(1)若点为边和边上的高的交点,求证:;
(2)若点不与三角形高的交点重合,的与是否还有上述关系?请说明理由.
28.对于点和图形,若在图形上存在不重合的点和点,使得点关于线段中点的对称点在图形上,则称点是图形的的“中称点”.在平面直角坐标系中,已知点,,.
(1)在点,,,中,是正方形的“中称点”;
(2)的圆心在轴上,半径为1.
①当圆心与原点重合时,若直线上存在的“中称点”,求的取值范围;
②若正方形的“中称点”都是的“中称点”,直接写出圆心的横坐标的取值范围.
初三数学试卷
2024年2月
班级________________姓名________________学号________________
考生须知 1.本试卷共4页,满分100分,考试时间120分钟。2.试卷答案一律填涂在答题卡或书写在答题纸上,在试卷上作答无效。3.在答题卡上,用2B铅笔作答,在答题纸上,用黑色字迹签字笔作答。4.考试结束后,将答题卡、答题纸一并交回。
一、选择题(本题共16分,每小题2分。在每小题给出的四个选项中,只有一项符合题目的要求。把正确答案涂写在答题纸上相应的位置。)
1.2023年5月30日神舟十六号载人飞船发射取得圆满成功,此次任务是我国载人航天工程进入空间站应用与发展阶段的首次载人飞行任务.下列有关航天的4个图标图案中是中心对称图形的是( )
A. B. C. D.
2.抛物线的顶点坐标是( )
A. B. C. D.
3.将一元二次方程通过配方转化为的形式,下列结果中正确的是( )
A. B. C. D.
4.如图,是的一条弦,直径是,若,垂足为,,,则的长度为( )
A.5 B.6 C.8 D.10
5.实数、、在数轴上对应点的位置如图所示.如果,那么下列结论正确的是( )
A. B. C. D.
5.不透明的袋子中有两个小球,上面分别写着数字“1”,“2”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )
A. B. C. D.
7.根据下列表格中二次函数的自变量与函数值的对应值,判断方程(,,,为常数)的一个解的范围是( )
6.17 6.18 6.19 6.20
0.02 0.04
A. B. C. D.
8.目标完成率,一般是指个体的实际完成量与目标完成量的比值,树立明确具体的目标,能够促使人们更好地完成任务.某读书会有10位成员(编号分别为),如图是根据他们年初制定的目标阅读量和年末实际完成情况绘制的统计图,下列结论正确的有( )
①目标完成率为100%的是,;
②目标阅读量与实际阅读量相差最多的是;
③目标完成率最高的是,最低的是;
④目标完成率超过75%且实际阅读量不少于5本的有三人.
A.①② B.①②③ C.①③④ D.①②③④
二、填空题(本题共8道小题,每小题2分,共16分)
9.因式分解:________.
10.二次函数的图象与轴的交点坐标为________.
11.若点,,在抛物线上,则,,的大小关系为________(用“”连接).
12.如图,将绕点逆时针旋转一定角度,得到,若,,且,则的度数为________.
13.如图,点,,,在上,,,,则________.
14.如图,是的直径,点在的延长线上,切于点,如果,,那么线段的长是________.
15.的顶点、、在边长为1的正方形网格的格点上,于点.则长为________.
16.如图,在中,,,正方形的边长为2,将正方形绕点旋转一周,连接,点为的中点,连接,则线段的最大值是________.
三、解答题(本题共68分,第17—18题,每小题5分,第19题4分,第20—21题,每小题5分,第22—26题,每小题6分,第27,28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17.计算:.
18.解不等式组,并写出它的所有非负整数解.
19.阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:为外一点.
求作:经过点的的切线.
小敏的作法如下:
如图,
①连接,作线段的垂直平分线交于点.
②以点为圆心,的长为半径作圆,交于,两点.
③作直线,.
(1)请补充完整小敏的作图;
(2)连接,可证,其依据是________.由此可证明直线,都是的切线,其依据是________.
20.已知,关于的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若该方程有一个根是负数,求的取值范围.
21.如图,在中,,点,,分别为,,的中点.
(1)求证:四边形是菱形;
(2)若,,求四边形的面积.
22.对于拋物线.
(1)它与轴交点的坐标为________,与轴交点的坐标为________,顶点坐标为________;
(2)在坐标系中利用描点法画出此抛物线;
(3)当时,结合函数图象,直接写出的取值范围________;
(4)若点,在抛物线上,且,直接写出的取值范围________.
23.在平面直角坐标系中,直线与轴交于点,直线:经过点,且与轴交于点.
(1)求点和点的坐标及直线的解析式;
(2)直线与直线关于直线对称,若直线与直线,围成的区域内(不包含边界)恰有1个整点,直接写出的取值范围.(注:横、纵坐标都是整数的点叫做整点.)
24.如图,在中,,为的直径,与相交于点,过点作于点,延长线交于点.
(1)求证:为的切线;
(2)若,,求的长.
25.通常把脏衣服用洗衣液清洗后会进行拧干,但由于不可能拧净衣服上的全部污水,所以还需要用清水进行多次漂洗,不断降低衣服中污水的含量.某小组研究了如何用清水漂洗衣服效果更好,部分内容如下,请补充完整:实验研究:先准备几件相同的洗过一次并拧干(存留一些污水)的衣服,把每件衣服分别用一定量的清水浸泡,经过充分搓洗,使清水与衣服上存留的污水混合均匀,然后拧干,视为一次漂洗,称重、记录每次漂洗后衣服上存留的污水重量和比例,如:把一件存留1斤污水的衣服用10斤清水漂洗后,拧干到仍然存留1斤污水,则漂洗后衣服中存有的污物是原来的,在多次实验后,通过对收集的数据进行分析,该小组决定使用20斤清水,采用三种不同的方案,对每件衣服分别进行漂洗,并假设每次拧干后的衣服上都存留约1斤的污水.
数据计算:对三种漂洗方案进行计算、比较.
方案一:采用一次漂洗的方式.将20斤清水一次用掉,漂洗后衣服中存有的污物是原来的________;
方案二:采用两次漂洗的方式,且两次用水量不同.如第一次用12斤清水,第二次用8斤清水,漂洗后衣服中存有的污物是原来的________;
方案三:采用两次漂洗的方式,且两次用水量相同,每次用10斤清水,漂洗后衣服中存有的污物是原来的________.
实验结论:对比可知,在这三种方案中,方案________的漂洗效果最好(填“一”“二”或“三”).
推广证明:将脏衣服用洗衣液清洗后,再用清水进行漂洗,假设每次拧干后还存留()斤污水,现用()斤清水漂洗(方案二中第一次用水量为斤),请比较并证明方案二与方案三的漂洗效果。
26.在平面直角坐标系中,点,在抛物线上,设抛物线的对称轴为.
(1)当时,求抛物线与轴交点的坐标及的值;
(2)点在抛物线上,若,求的取值范围及的取值范围.
27.已知,点为中点,,为边,上的动点,且满足,为平面内一点,,,连结,.
(1)若点为边和边上的高的交点,求证:;
(2)若点不与三角形高的交点重合,的与是否还有上述关系?请说明理由.
28.对于点和图形,若在图形上存在不重合的点和点,使得点关于线段中点的对称点在图形上,则称点是图形的的“中称点”.在平面直角坐标系中,已知点,,.
(1)在点,,,中,是正方形的“中称点”;
(2)的圆心在轴上,半径为1.
①当圆心与原点重合时,若直线上存在的“中称点”,求的取值范围;
②若正方形的“中称点”都是的“中称点”,直接写出圆心的横坐标的取值范围.
同课章节目录
