安徽省合肥市包河区智育联盟2023-2024学年九年级上学期期末数学试题(含答案)
文档属性
| 名称 | 安徽省合肥市包河区智育联盟2023-2024学年九年级上学期期末数学试题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 944.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 00:00:00 | ||
图片预览



文档简介
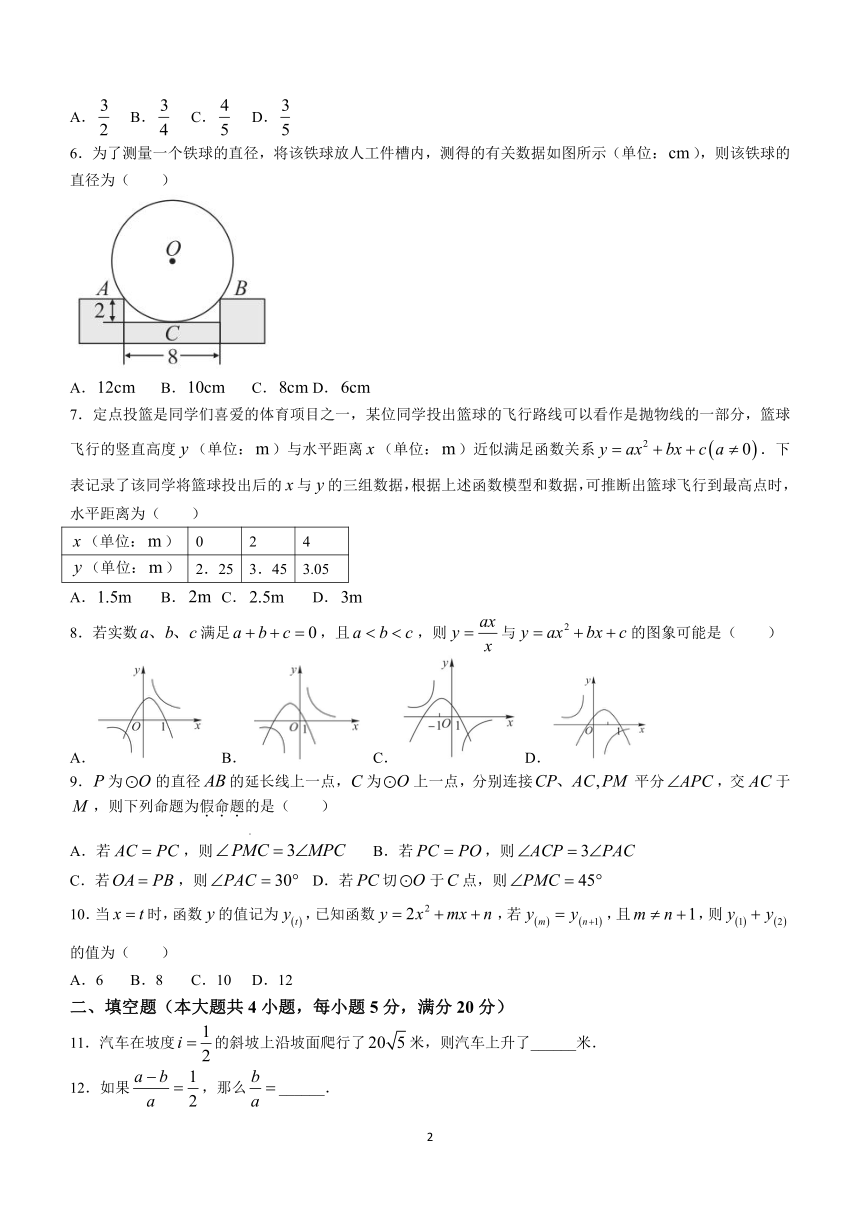
九年级数学核心素养评价
满分:150分 考试时间:120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图案中,是中心对称图形的是( )
A. B. C. D.
2.将二次函数的图象向右平移2个单位,再向下平移3个单位,得到的函数图象的表达式是( )
A. B. C. D.
3.如图,中,点分别在上,.若,则与的面积之比为( )
A. B. C. D.
4.如图,是的直径,点是圆上两点,且,则等于( )
A. B. C. D.
5.如图,的顶点都在方格纸的格点上,那么的值为( )
A. B. C. D.
6.为了测量一个铁球的直径,将该铁球放人工件槽内,测得的有关数据如图所示(单位:),则该铁球的直径为( )
A. B. C. D.
7.定点投篮是同学们喜爱的体育项目之一,某位同学投出篮球的飞行路线可以看作是抛物线的一部分,篮球飞行的竖直高度(单位:)与水平距离(单位:)近似满足函数关系.下表记录了该同学将篮球投出后的与的三组数据,根据上述函数模型和数据,可推断出篮球飞行到最高点时,水平距离为( )
(单位:) 0 2 4
(单位:) 2.25 3.45 3.05
A. B. C. D.
8.若实数满足,且,则与的图象可能是( )
A. B. C. D.
9.为的直径的延长线上一点,为上一点,分别连接平分,交于,则下列命题为假命题的是( )
A.若,则 B.若,则
C.若,则 D.若切于点,则
10.当时,函数的值记为,已知函数,若,且,则的值为( )
A.6 B.8 C.10 D.12
二、填空题(本大题共4小题,每小题5分,满分20分)
11.汽车在坡度的斜坡上沿坡面爬行了米,则汽车上升了______米.
12.如果,那么______.
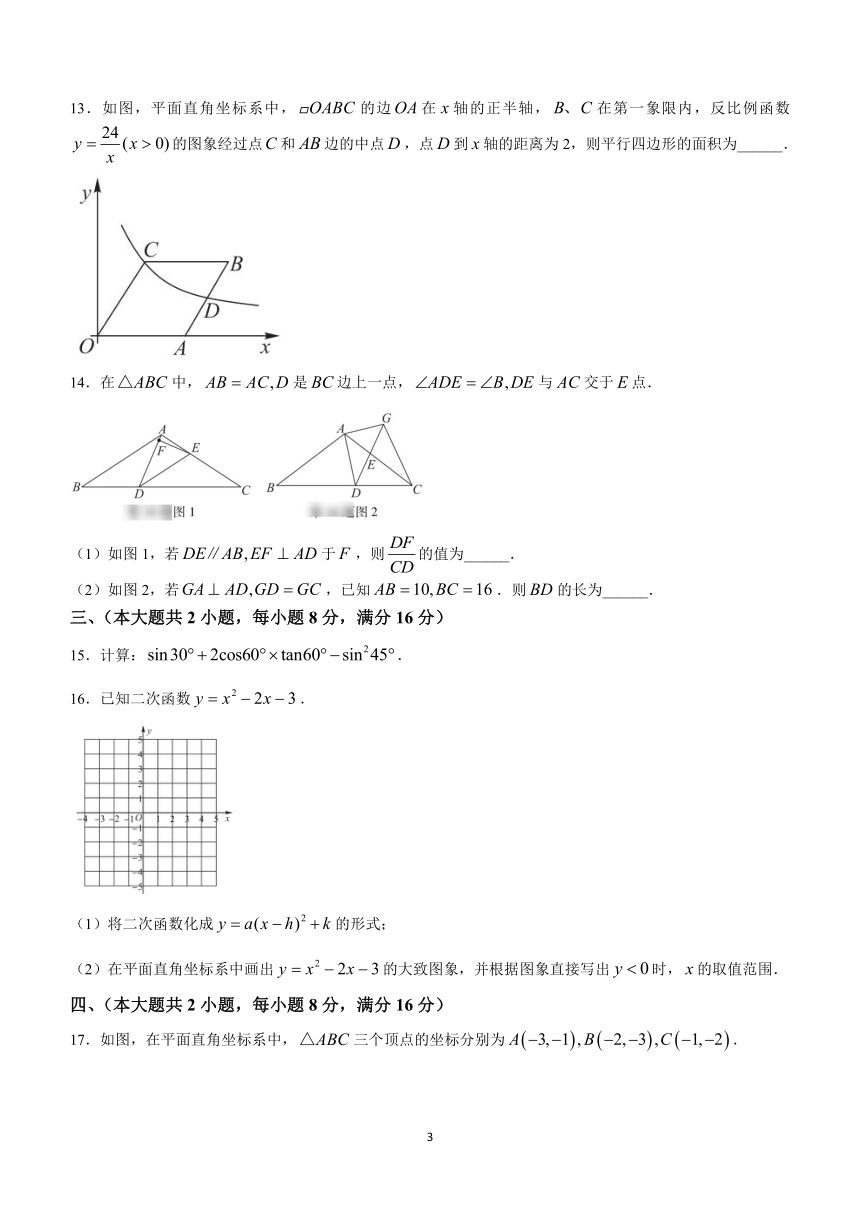
13.如图,平面直角坐标系中,的边在轴的正半轴,在第一象限内,反比例函数的图象经过点和边的中点,点到轴的距离为2,则平行四边形的面积为______.
14.在中,是边上一点,与交于点.
(1)如图1,若于,则的值为______.
(2)如图2,若,已知.则的长为______.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:.
16.已知二次函数.
(1)将二次函数化成的形式;
(2)在平面直角坐标系中画出的大致图象,并根据图象直接写出时,的取值范围.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在平面直角坐标系中,三个顶点的坐标分别为.
(1)以为旋转中心,将顺时针旋转得到,并写出点的坐标
(2)以为位似中心,在第一象限内作出的位似,且与的位似比为.
18.周末,数学探究小组利用无人机在合肥园博园开展测量信标塔高度的活动,此时无人机在高出地面80米的点处,操控者站在点处,无人机测得点的俯角为.测得信标塔顶点处的俯角为,操控者和信标塔的距离为102米,求信标塔的高度(结果保留整数,参考数据:).
五、(本大题共2小题,每小题10分,满分20分)
19.已知:菱形中,为中点,交于,且.
(1)求证:;
(2)若,求的长.
20.悬索桥是现代高架桥的主要结构方式,如图是某悬索桥的截面示意图,主索近似符合抛物线,从主索上设置竖直的吊索,与桥面垂直,并连接桥面承接桥面的重量,两桥塔,间距为,桥面水平,主索最低点为点,点距离桥面为,以中点为原点,所在直线为轴,建立平面直角坐标系.
(1)写出点的坐标,并求出主索抛物线的表达式;
(2)距离点水平距离为和处的吊索共四条需要更换,求四根吊索总长度为多少米
六、(本题满分12分)
21.如图,是的直径,点是圆上一点,点是半圆的中点,连接交于点,过点作的切线交延长线于.
(1)求证:;
(2)若,求半径的长.
七、(本题满分12分)
22.已知在平面直角坐标系中,二次函数的图象经过点和点.
(1)求该函数的解析式.
(2)平移抛物线,平移后的图象记为图象,其顶点在抛物线上,直线分别与抛物线和函数图象交于点和点,求线段长的最大值.
八、(本题满分14分)
23.如图1,中,于点在边上,交于,过点作于点.
(1)求证:;
(2)如图2,当时,求的长;
(3)连接,若,求的值.
智育联盟2023—2024年度第一学期期末
九年级数学 参考答案和评分标准
1----5: BADAD 6----10:BCDCB
8.提示:a、c异号,当时,∴,故C错误;当时,,故选D.
10.解析:由抛物线对称轴可知 ∴
11. 20 12. 13. 36 14.(1) (2)
13.【解析】∵点D的纵坐标为2,故 ∴点D的坐标为(12,2)
∵点D为AB中点,∴点C的纵坐标为4,∴ ∴C(6,4)
∴ ∴
14.(1)解:作EI⊥CD于I,∵AB=AC ∴∠B=∠C
∵DE∥AB,∴∠EDC=∠B,
∵∠ADE=∠B,∴∠ADE=∠EDC=∠C,
∴ED=EC,
∵DE平分∠ADC,∴DF=DI,
∵CD=2DI,∴;
(2)作AM⊥BC于M,GH⊥CD于H,AN⊥GH,交HG的延长线于N,
易得四边形AMHN是矩形,△AGN∽△ADM,
△ADG∽△MBA,∴,
∴,
∴,
∴CD=7,BD=16-7=9.
15.原式 = ……………………6分
= ……………………8分
16.(1) ……………………3分
(2)图象略 ……………………6分
……………………8分
17.(1)如图;(-1,3) ……………………4分
(2)如图. ……………………8分
18.解:如图,过点D作DE⊥AB于E,过点C作CF⊥DE于F,
由题意得AB=102,DE=80,∠DAB=53°,∠DCF=25°,
在Rt△ADE中,tan∠DAE=tan53°=,∴(米)
∴(米) ……………………4分
∵CB⊥BE,FE⊥BE,CF⊥EF,∴四边形BCFE为矩形,
∴(米)
在Rt△DFC中,∠DCF=25°,
∴(米)
∴BC=DE-DF=80-19.7=60.3≈60(米)
∴信标塔BC的高度为约为60米. ……………………8分
19.证明:(1)∵菱形ABCD ∴AB∥CD AD∥BC
∵∠ADB=∠BCE ∴∠FBC=∠FCB ∴FB=FC ∵AB∥CD ∴△BEF∽△DCF
∴ ∴E为AB中点 ∴ ∴FC=2EF ∴FB=2EF ………………4分
(2)设BE=1,EF=x,则BF=FC=2x,EC=3x
∵AB=AD ∴∠ADB=∠ABD=∠BCE ∵∠BEF=∠BEF ∴△BEF∽△CEB
∴ ∴ ∴ ∴ . ……………………10分
20.解:设抛物线的表达式为
由题意可知,C点坐标为(16,0),P点坐标为(0,-8)
将C(16,0),P(0,-8)代入,得
解得.
∴主索抛物线的表达式为 ……………………4分
(2)x=4时,,此时吊索的长度为m
由抛物线的对称性可得,x=-4时,此时吊索的长度也为m.
同理,x=8时,,此时吊索的长度为m
x=-8时,此时吊索的长度也为4m.
∴四根吊索的总长度为13m. ……………………10分
21.(1)证明:连接OC、OD.
∵点D是半圆的中点,∴∠AOD=∠BOD=90° ∴∠D+∠OED=90°.
∵OD=OC,∴∠D=∠OCD.
又∵FC是⊙O的切线 ∴∠OCF=90° 即∠OCD+∠FCE=90°
∴∠FCE=∠OED.
∵∠FEC=∠OED,∴∠FCE=∠FEC. ∴CF=EF. ……………………6分
(2)∵tanA=,∴在Rt△ABC中,=.
∵∠ACB=∠OCF=90°,∴∠ACO=∠BCF=∠A.
∵△ACF∽△CBF,∴.
∴AF=10. ∴CF2=BF·AF.
∴BF=. ∴AO==. ……………………12分
22.解:(1)∵二次函数的图象经过点(,0)和点(,),
∴,解得,
∴该函数的解析式为; ……………………4分
(2)平移抛物线,其顶点始终在二次函数上,
∴设顶点坐标为(h,),故平移后的解析式为,
∴,
∵直线分别与抛物线和函数图象G交于点P和点Q,
∴(),
∵, ∴当时,PQ长的最大值为. ……………………12分
23.解:(1)∵CE=CB ∴∠CEB=∠CBE
∵∠ADB=90°,AD=BD ∴∠A=∠ABD=45°
又∴∠ACE=∠CEB-∠A ∠DBC=∠CBE-∠ABD
∴ ∠ACE=∠DBC ∴△CGE≌△BDC
∴GE=DC. ……………………4分
(2)由(1)知△CGE≌△BDC
∴GC=BD=2DF=4
设CD=GE=x ∵GE//BD
∵ ∴ 解得
在Rt△DCB中,, BD=AD=4,∴. ……………………8分
(3)∵DE//BC ∴∠DEA=∠CBA=∠CEB
∴△DAE∽△FBE ∴ ∴BF=CD
∵∠ACE=∠DBC ∴△DCF∽△DBC
∴
设DB=DA=1, BF=CD=x
∴ 解得
∴. ……………………14分
满分:150分 考试时间:120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图案中,是中心对称图形的是( )
A. B. C. D.
2.将二次函数的图象向右平移2个单位,再向下平移3个单位,得到的函数图象的表达式是( )
A. B. C. D.
3.如图,中,点分别在上,.若,则与的面积之比为( )
A. B. C. D.
4.如图,是的直径,点是圆上两点,且,则等于( )
A. B. C. D.
5.如图,的顶点都在方格纸的格点上,那么的值为( )
A. B. C. D.
6.为了测量一个铁球的直径,将该铁球放人工件槽内,测得的有关数据如图所示(单位:),则该铁球的直径为( )
A. B. C. D.
7.定点投篮是同学们喜爱的体育项目之一,某位同学投出篮球的飞行路线可以看作是抛物线的一部分,篮球飞行的竖直高度(单位:)与水平距离(单位:)近似满足函数关系.下表记录了该同学将篮球投出后的与的三组数据,根据上述函数模型和数据,可推断出篮球飞行到最高点时,水平距离为( )
(单位:) 0 2 4
(单位:) 2.25 3.45 3.05
A. B. C. D.
8.若实数满足,且,则与的图象可能是( )
A. B. C. D.
9.为的直径的延长线上一点,为上一点,分别连接平分,交于,则下列命题为假命题的是( )
A.若,则 B.若,则
C.若,则 D.若切于点,则
10.当时,函数的值记为,已知函数,若,且,则的值为( )
A.6 B.8 C.10 D.12
二、填空题(本大题共4小题,每小题5分,满分20分)
11.汽车在坡度的斜坡上沿坡面爬行了米,则汽车上升了______米.
12.如果,那么______.
13.如图,平面直角坐标系中,的边在轴的正半轴,在第一象限内,反比例函数的图象经过点和边的中点,点到轴的距离为2,则平行四边形的面积为______.
14.在中,是边上一点,与交于点.
(1)如图1,若于,则的值为______.
(2)如图2,若,已知.则的长为______.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:.
16.已知二次函数.
(1)将二次函数化成的形式;
(2)在平面直角坐标系中画出的大致图象,并根据图象直接写出时,的取值范围.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在平面直角坐标系中,三个顶点的坐标分别为.
(1)以为旋转中心,将顺时针旋转得到,并写出点的坐标
(2)以为位似中心,在第一象限内作出的位似,且与的位似比为.
18.周末,数学探究小组利用无人机在合肥园博园开展测量信标塔高度的活动,此时无人机在高出地面80米的点处,操控者站在点处,无人机测得点的俯角为.测得信标塔顶点处的俯角为,操控者和信标塔的距离为102米,求信标塔的高度(结果保留整数,参考数据:).
五、(本大题共2小题,每小题10分,满分20分)
19.已知:菱形中,为中点,交于,且.
(1)求证:;
(2)若,求的长.
20.悬索桥是现代高架桥的主要结构方式,如图是某悬索桥的截面示意图,主索近似符合抛物线,从主索上设置竖直的吊索,与桥面垂直,并连接桥面承接桥面的重量,两桥塔,间距为,桥面水平,主索最低点为点,点距离桥面为,以中点为原点,所在直线为轴,建立平面直角坐标系.
(1)写出点的坐标,并求出主索抛物线的表达式;
(2)距离点水平距离为和处的吊索共四条需要更换,求四根吊索总长度为多少米
六、(本题满分12分)
21.如图,是的直径,点是圆上一点,点是半圆的中点,连接交于点,过点作的切线交延长线于.
(1)求证:;
(2)若,求半径的长.
七、(本题满分12分)
22.已知在平面直角坐标系中,二次函数的图象经过点和点.
(1)求该函数的解析式.
(2)平移抛物线,平移后的图象记为图象,其顶点在抛物线上,直线分别与抛物线和函数图象交于点和点,求线段长的最大值.
八、(本题满分14分)
23.如图1,中,于点在边上,交于,过点作于点.
(1)求证:;
(2)如图2,当时,求的长;
(3)连接,若,求的值.
智育联盟2023—2024年度第一学期期末
九年级数学 参考答案和评分标准
1----5: BADAD 6----10:BCDCB
8.提示:a、c异号,当时,∴,故C错误;当时,,故选D.
10.解析:由抛物线对称轴可知 ∴
11. 20 12. 13. 36 14.(1) (2)
13.【解析】∵点D的纵坐标为2,故 ∴点D的坐标为(12,2)
∵点D为AB中点,∴点C的纵坐标为4,∴ ∴C(6,4)
∴ ∴
14.(1)解:作EI⊥CD于I,∵AB=AC ∴∠B=∠C
∵DE∥AB,∴∠EDC=∠B,
∵∠ADE=∠B,∴∠ADE=∠EDC=∠C,
∴ED=EC,
∵DE平分∠ADC,∴DF=DI,
∵CD=2DI,∴;
(2)作AM⊥BC于M,GH⊥CD于H,AN⊥GH,交HG的延长线于N,
易得四边形AMHN是矩形,△AGN∽△ADM,
△ADG∽△MBA,∴,
∴,
∴,
∴CD=7,BD=16-7=9.
15.原式 = ……………………6分
= ……………………8分
16.(1) ……………………3分
(2)图象略 ……………………6分
……………………8分
17.(1)如图;(-1,3) ……………………4分
(2)如图. ……………………8分
18.解:如图,过点D作DE⊥AB于E,过点C作CF⊥DE于F,
由题意得AB=102,DE=80,∠DAB=53°,∠DCF=25°,
在Rt△ADE中,tan∠DAE=tan53°=,∴(米)
∴(米) ……………………4分
∵CB⊥BE,FE⊥BE,CF⊥EF,∴四边形BCFE为矩形,
∴(米)
在Rt△DFC中,∠DCF=25°,
∴(米)
∴BC=DE-DF=80-19.7=60.3≈60(米)
∴信标塔BC的高度为约为60米. ……………………8分
19.证明:(1)∵菱形ABCD ∴AB∥CD AD∥BC
∵∠ADB=∠BCE ∴∠FBC=∠FCB ∴FB=FC ∵AB∥CD ∴△BEF∽△DCF
∴ ∴E为AB中点 ∴ ∴FC=2EF ∴FB=2EF ………………4分
(2)设BE=1,EF=x,则BF=FC=2x,EC=3x
∵AB=AD ∴∠ADB=∠ABD=∠BCE ∵∠BEF=∠BEF ∴△BEF∽△CEB
∴ ∴ ∴ ∴ . ……………………10分
20.解:设抛物线的表达式为
由题意可知,C点坐标为(16,0),P点坐标为(0,-8)
将C(16,0),P(0,-8)代入,得
解得.
∴主索抛物线的表达式为 ……………………4分
(2)x=4时,,此时吊索的长度为m
由抛物线的对称性可得,x=-4时,此时吊索的长度也为m.
同理,x=8时,,此时吊索的长度为m
x=-8时,此时吊索的长度也为4m.
∴四根吊索的总长度为13m. ……………………10分
21.(1)证明:连接OC、OD.
∵点D是半圆的中点,∴∠AOD=∠BOD=90° ∴∠D+∠OED=90°.
∵OD=OC,∴∠D=∠OCD.
又∵FC是⊙O的切线 ∴∠OCF=90° 即∠OCD+∠FCE=90°
∴∠FCE=∠OED.
∵∠FEC=∠OED,∴∠FCE=∠FEC. ∴CF=EF. ……………………6分
(2)∵tanA=,∴在Rt△ABC中,=.
∵∠ACB=∠OCF=90°,∴∠ACO=∠BCF=∠A.
∵△ACF∽△CBF,∴.
∴AF=10. ∴CF2=BF·AF.
∴BF=. ∴AO==. ……………………12分
22.解:(1)∵二次函数的图象经过点(,0)和点(,),
∴,解得,
∴该函数的解析式为; ……………………4分
(2)平移抛物线,其顶点始终在二次函数上,
∴设顶点坐标为(h,),故平移后的解析式为,
∴,
∵直线分别与抛物线和函数图象G交于点P和点Q,
∴(),
∵, ∴当时,PQ长的最大值为. ……………………12分
23.解:(1)∵CE=CB ∴∠CEB=∠CBE
∵∠ADB=90°,AD=BD ∴∠A=∠ABD=45°
又∴∠ACE=∠CEB-∠A ∠DBC=∠CBE-∠ABD
∴ ∠ACE=∠DBC ∴△CGE≌△BDC
∴GE=DC. ……………………4分
(2)由(1)知△CGE≌△BDC
∴GC=BD=2DF=4
设CD=GE=x ∵GE//BD
∵ ∴ 解得
在Rt△DCB中,, BD=AD=4,∴. ……………………8分
(3)∵DE//BC ∴∠DEA=∠CBA=∠CEB
∴△DAE∽△FBE ∴ ∴BF=CD
∵∠ACE=∠DBC ∴△DCF∽△DBC
∴
设DB=DA=1, BF=CD=x
∴ 解得
∴. ……………………14分
同课章节目录
