一次函数的复习

课件22张PPT。 一次函数复习变量与常量: 不同的事物的变化过程中，有些量的值是按某种规律在变化，有些量的值是始终不变的。
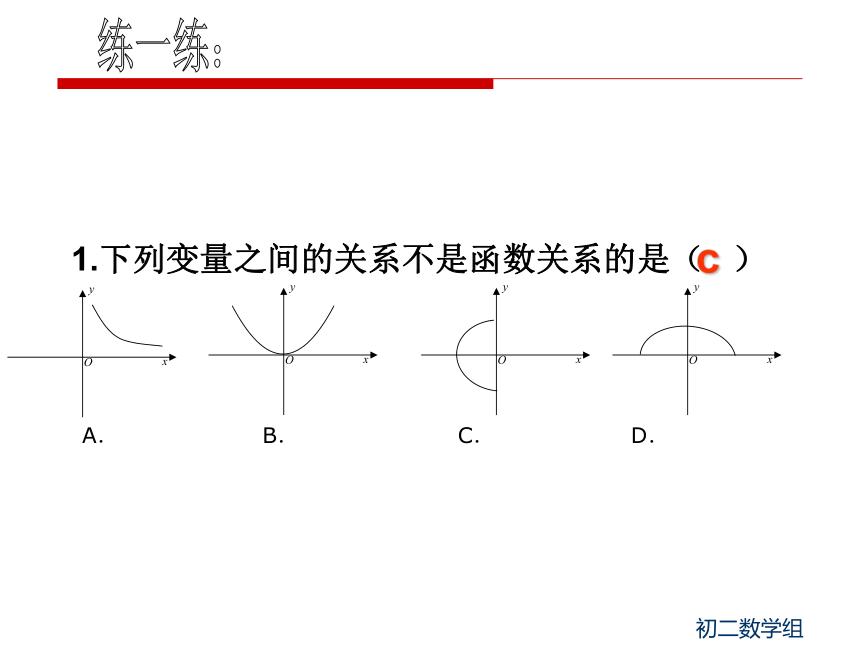
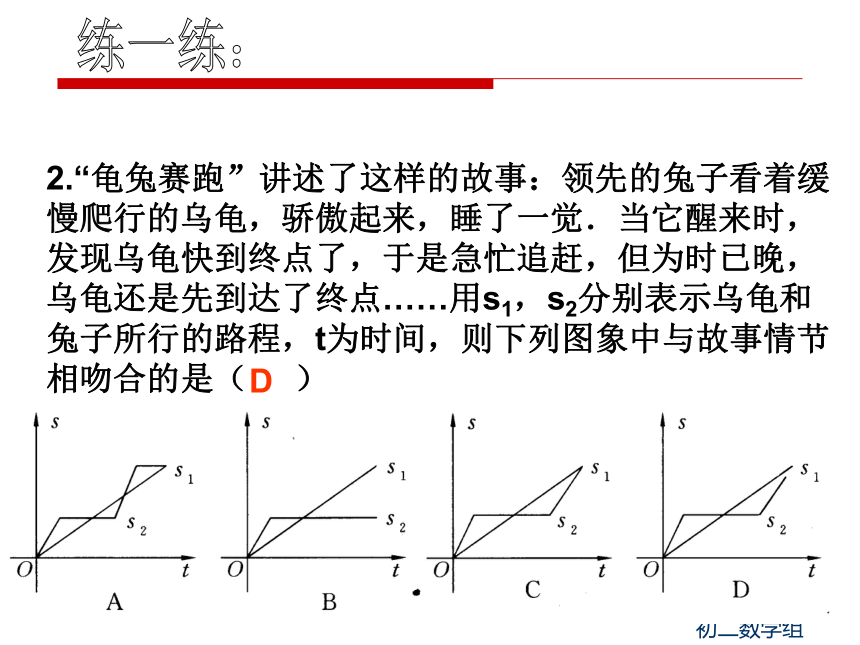
在一个变化过程中，我们称数值发生变化的量为变量，数值始终不变的量为常量。函数的概念： 一般地，在一个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数.练一练：c 练一练：2.“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来，睡了一觉．当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点……用s1，s2分别表示乌龟和兔子所行的路程，t为时间，则下列图象中与故事情节相吻合的是（ ）D 你知道一次函数的哪些知识？
我们从哪些方面进行研究的？（从定义、图象、性质、应用等方面）交流与讨论一、定义：　　1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。当b_____时，函数y=____(k____)叫做正比例函数。kx ＋b≠０ = ０≠０kx★3、理解一次函数概念应注意下面两点：
　　⑴、解析式中自变量x的次数是___次，
⑵、自变量系数_____。1k≠0回顾与反思 　　
　　 2、一次函数y=kx+b(k≠0)的图象是过点（0，
___) ,(______,0)的__________。b一条直线二、图象与性质4、一次函数y=kx+b(k ≠ 0)的性质：
　　⑴当k>0时，y随x的增大而_________。
　　⑵当k<0时，y随x的增大而_________。
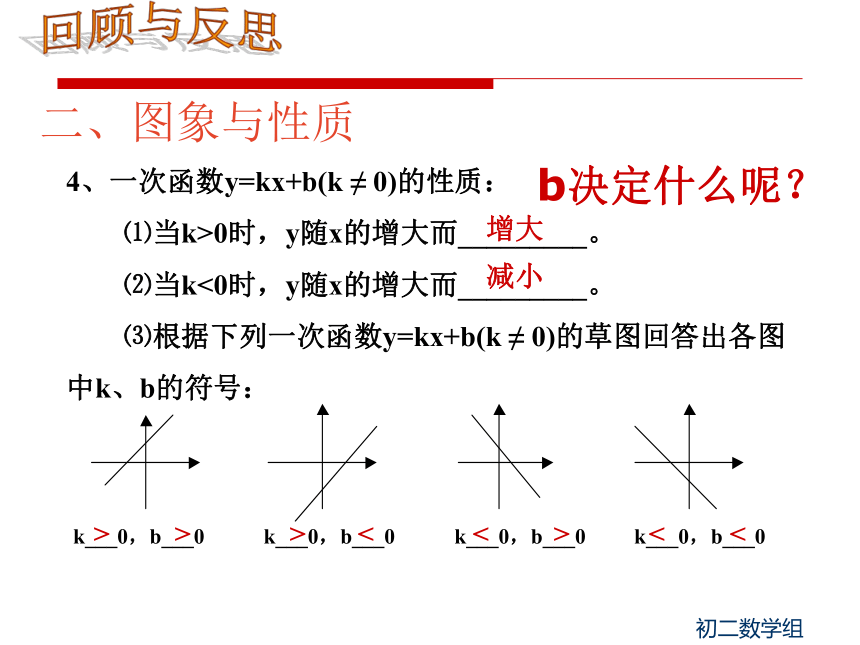
　　⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号：增大减小k___0，b___0 k___0，b___0 k___0，b___0 k___0，b___0<<><<>>>回顾与反思b决定什么呢？②①、②、③④③　　(2)、如果一次函数y=kx-3k+6的图象经过(2,1)，那么
k的值为________。k=5此函数恒过一个点，你知道是什么吗？二、图象与性质回顾与反思三、图象平移、旋转、对称回顾与反思（1）根据已知条件写出含有待定系数的解析式（定型）（2）将x，y的几对值或图象上点的坐标代入上述解析式，
得到以待定系数为未知数的方程或方程组，并解
方程（组），得到待定的系数的值 （定系数）（3）将求出的待定系数代回所求的函数关系式中，得到
所求函数的解析式 （定式）求一次函数的解析式，只要确定k和b两个常数即可；
求正比例函数的解析式，只要确定k一个系数即可。四、如何确定函数的关系式常见的求关系式问题：2、已知一次函数y=kx+b(k≠0)平行于
直线y=3x，且过点(1,4)，求函数关系式。函数关系式为：y=3x+11、已知某一次函数的图象经过(3, 4), (-2, 0)两点,试求这个一次函数的解析式.★★3、已知某一次函数的图象经过(3, 4),且与直线y=x-1交于点A,点A到X轴的距离为1,试求这个一次函数的关系式.
常见的求关系式问题：（1）求出函数关系式时，
必须注意自变量的取值范围。
（2）实际问题中，图象应根据
函数自变量的取值范围来确定。小提醒常见的一次函数应用问题一、图象信息决策题赏析1、 A、B两船同时从相距450海里的甲、乙两港相向而行，s（海里）表示轮船与甲港的距离，t（分钟）表示轮船行驶的时间，如图所示，l1、l2分别表示两船的s与t的关系。
（1）l1表示哪只轮船到甲港的距离与行驶时间的关系？
（2）A、B两船的速度各是多少？
常见的应用问题一、图象信息题赏析1、 A、B两船同时从相距450海里的甲、乙两港相向而行，s（海里）表示轮船与甲港的距离，t（分钟）表示轮船行驶的时间，如图所示，l1、l2分别表示两船的s与t的关系。
（3）分别写出两船到甲港距离s与行驶时间t的关系。
★（4）两小时后，A、B两船相距多少海里？
（5）航行多长时间后，A、B两船相相遇？
★★ （6）航行多长时间后，A、B两船相150海里？
二、图象切割问题常见的应用问题 赏析2、 某医药研究所开发了一种新药，在试验效时发现，如果成人按规定剂量服用，那么服药后2小时血液中含药量最高，达每毫升6微克（1微克=10－3毫克），接着逐步衰减，10小时血液中含药量为每毫升3微克，每毫升血液中含药量y（微克）随时间x（小时）的变化如图所示，当成人规定剂量服药后：
（1）分别求出x≤2和x≥2时y与x之间的函数关系式。
y()二、图象切割问题常见的应用问题 赏析2、 某医药研究所开发了一种新药，在试验效时发现，如果成人按规定剂量服用，那么服药后2小时血液中含药量最高，达每毫升6微克（1微克=10－3毫克），接着逐步衰减，10小时血液中含药量为每毫升3微克，每毫升血液中含药量y（微克）随时间x（小时）的变化如图所示，当成人规定剂量服药后：
y()
★（2）如果每毫升血液中含药量为4微克或4微克以上时对于治疗疾病时是有效的，那么这个有效时间是多长？xy210364二、图象切割问题常见的应用问题 赏析2、 某医药研究所开发了一种新药，在试验效时发现，如果成人按规定剂量服用，那么服药后2小时血液中含药量最高，达每毫升6微克（1微克=10－3毫克），接着逐步衰减，10小时血液中含药量为每毫升3微克，每毫升血液中含药量y（微克）随时间x（小时）的变化如图所示，当成人规定剂量服药后：
y()
★★（3）如果每毫升血液中含药量不少于2微克，但不高于5微克时对于治疗疾病时是有效的，那么这个有效时间是多长？二、图象切割问题常见的应用问题 赏析2、 某医药研究所开发了一种新药，在试验效时发现，如果成人按规定剂量服用，那么服药后2小时血液中含药量最高，达每毫升6微克（1微克=10－3毫克），接着逐步衰减，10小时血液中含药量为每毫升3微克，每毫升血液中含药量y（微克）随时间x（小时）的变化如图所示，当成人规定剂量服药后：
y()
★★★（4）从第1小时到第15小时人体内的药含量的变化范围是多少呢？ 你在学习一次函数的过程中，哪一个内容你学得最有成就感、最让你震撼，为什么？与大家分享一下！ 谢谢大家，真诚地希
望您能提出宝贵
的意见 ！