澄迈县青年数学教师说课评比优秀课件之《相似三角形的性质》
文档属性
| 名称 | 澄迈县青年数学教师说课评比优秀课件之《相似三角形的性质》 |

|
|
| 格式 | rar | ||
| 文件大小 | 151.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-03 00:00:00 | ||
图片预览






文档简介
课件15张PPT。《相似三角形的性质》说课九年级上册§24.3.3说课教师 李庆武澄迈县加乐中学
《相似三角形的性质》1、教材地位及作用
2、教学内容及教材处理
3、教学目标
4、教学重点与难点一、教材分析二、教法分析三、教学过程1、教学思想与策略
2、教学模式
教学目标(1)知识与技能
学生通过观察、探究、猜想、证明的学习活动,理解和掌握相似三角形的有关性质。(2)过程与方法
学生经历“观察探究—问题猜想—推理证明—感悟收获”的学习过程,体会探究发现问题和体验利用数学证明解决的思想。通过分析、归纳、证明发展逻辑思维,提高数学表达及综合分析问题的能力。 (3)情感态度与价值观
学生在和谐、民主、活跃的学习氛围中,感受学习数学的乐趣,养成良好的学习习惯和勤于思考、勇于探索的思维品质。教学重点:探索相似三角形的有关性质。
教学难点:相似三角形有关性质的证明思路。
突破难点的关键:确定证明的关键点。教学重点与难点教学环节一、复习旧知、引入新课七、主要板书设计六、作业拓展五、课堂小结四、练习巩固三、思考2、问题2、31、问题1二、新课教学复习提问1、相似三角形的对应边、对应角之间分别有什么关系?判定两个三角形相似的方法有哪些?
2、若△ABC∽△A′B′C′且它们的相似比为K,则:—— = —— = —— =K
则: AB+BC+AC
—————————— =
A′B′+B′C′+A′C′ ——
3、揭示课题,明确目标
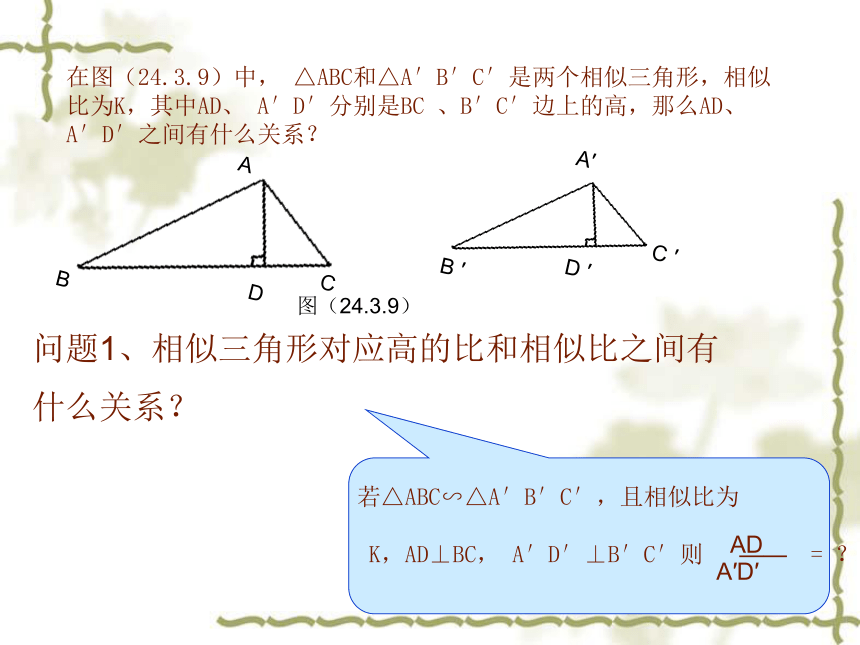
(板书课题:相似三角形的性质) 问题1、相似三角形对应高的比和相似比之间有 什么关系? 图(24.3.9) 若△ABC∽△A′B′C′,且相似比为
K,AD⊥BC, A′D′⊥B′C′则 —— = ?
在图(24.3.9)中, △ABC和△A′B′C′是两个相似三角形,相似比为K,其中AD、 A′D′分别是BC 、B′C′边上的高,那么AD、A′D′之间有什么关系?
图(24.3.9)由两三角形相似 → 得出相关条件 →证另两三角形相似
从而得出结论。证明思路:设计意图:
通过图形的分
解,把相似三
角形对应高的
比转化为,对
应边的比。过
程生动形象,
有助学生探索,
得出结论。问题2、相似三角形的面积比与相似比之间有什么关系? 问题3、相似三角形的周长比与相似比之间有什么关系?图24.3.10中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,
它们都相似你能从中得到什么结论?请完成以下填空例5 已知:△ABC∽△A′B′C′,且相似比为K,AD、A′D′
求证: 证明思路由已知两三角形相似 → 关键条件 → 代入公式从而得出结论 验证猜想分别为 △ABC、△A′B′C′对应边BC、B′C′上的高,分析:(1)证明相似三角形的面积比等于相似比的平方。(2)证明相似三角形的周长比等于相似比。 相似三角形的周长
比又怎样证明呢?想一想想一想:三角形的面积公式
是什么?设计意图:
找出证明关键,
突破证明难点,
归纳证明思路。
思考与证明如图(24.3.11)△ABC∽△A′B′C′,D、D′分别为BC、B′C′的中点,BE平分∠ABC, B′E′平∠A′B′C′ 。
那么它们之间有什么关系呢?1、相似三角形对应边上的中线的比是什么?2、相似三角形角平分线之间的比是什么? 练习巩固遵循巩固性原则,检验学生对所学知识的掌握程度 教材第61页练习1—3 课堂小结 本节课我们学习了哪些内容 通过本节课的探究学习,你和同伴交流的愉快吗?
你收获到了什么?你有何感受? 对应高
对应中线
对应角平分线
周长线的比等于相似比。面:面积的比等于相似比的平方。相似多边形也具有同样的性质。开放性作业布置 要求学生利用本节课所学,联系生活实际,设计应用问题,可采用多种途径完成,如:利用网络、深入生活,从现实生活中获取相关信息等。让学生与自己的同伴一起完成。 相似三角形的性质
性质:
……………… 1、证明:
………………
……………… 2、证明:
……………… 主要板书设计呈现主要内容,梳理知识结构。
《相似三角形的性质》1、教材地位及作用
2、教学内容及教材处理
3、教学目标
4、教学重点与难点一、教材分析二、教法分析三、教学过程1、教学思想与策略
2、教学模式
教学目标(1)知识与技能
学生通过观察、探究、猜想、证明的学习活动,理解和掌握相似三角形的有关性质。(2)过程与方法
学生经历“观察探究—问题猜想—推理证明—感悟收获”的学习过程,体会探究发现问题和体验利用数学证明解决的思想。通过分析、归纳、证明发展逻辑思维,提高数学表达及综合分析问题的能力。 (3)情感态度与价值观
学生在和谐、民主、活跃的学习氛围中,感受学习数学的乐趣,养成良好的学习习惯和勤于思考、勇于探索的思维品质。教学重点:探索相似三角形的有关性质。
教学难点:相似三角形有关性质的证明思路。
突破难点的关键:确定证明的关键点。教学重点与难点教学环节一、复习旧知、引入新课七、主要板书设计六、作业拓展五、课堂小结四、练习巩固三、思考2、问题2、31、问题1二、新课教学复习提问1、相似三角形的对应边、对应角之间分别有什么关系?判定两个三角形相似的方法有哪些?
2、若△ABC∽△A′B′C′且它们的相似比为K,则:—— = —— = —— =K
则: AB+BC+AC
—————————— =
A′B′+B′C′+A′C′ ——
3、揭示课题,明确目标
(板书课题:相似三角形的性质) 问题1、相似三角形对应高的比和相似比之间有 什么关系? 图(24.3.9) 若△ABC∽△A′B′C′,且相似比为
K,AD⊥BC, A′D′⊥B′C′则 —— = ?
在图(24.3.9)中, △ABC和△A′B′C′是两个相似三角形,相似比为K,其中AD、 A′D′分别是BC 、B′C′边上的高,那么AD、A′D′之间有什么关系?
图(24.3.9)由两三角形相似 → 得出相关条件 →证另两三角形相似
从而得出结论。证明思路:设计意图:
通过图形的分
解,把相似三
角形对应高的
比转化为,对
应边的比。过
程生动形象,
有助学生探索,
得出结论。问题2、相似三角形的面积比与相似比之间有什么关系? 问题3、相似三角形的周长比与相似比之间有什么关系?图24.3.10中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,
它们都相似你能从中得到什么结论?请完成以下填空例5 已知:△ABC∽△A′B′C′,且相似比为K,AD、A′D′
求证: 证明思路由已知两三角形相似 → 关键条件 → 代入公式从而得出结论 验证猜想分别为 △ABC、△A′B′C′对应边BC、B′C′上的高,分析:(1)证明相似三角形的面积比等于相似比的平方。(2)证明相似三角形的周长比等于相似比。 相似三角形的周长
比又怎样证明呢?想一想想一想:三角形的面积公式
是什么?设计意图:
找出证明关键,
突破证明难点,
归纳证明思路。
思考与证明如图(24.3.11)△ABC∽△A′B′C′,D、D′分别为BC、B′C′的中点,BE平分∠ABC, B′E′平∠A′B′C′ 。
那么它们之间有什么关系呢?1、相似三角形对应边上的中线的比是什么?2、相似三角形角平分线之间的比是什么? 练习巩固遵循巩固性原则,检验学生对所学知识的掌握程度 教材第61页练习1—3 课堂小结 本节课我们学习了哪些内容 通过本节课的探究学习,你和同伴交流的愉快吗?
你收获到了什么?你有何感受? 对应高
对应中线
对应角平分线
周长线的比等于相似比。面:面积的比等于相似比的平方。相似多边形也具有同样的性质。开放性作业布置 要求学生利用本节课所学,联系生活实际,设计应用问题,可采用多种途径完成,如:利用网络、深入生活,从现实生活中获取相关信息等。让学生与自己的同伴一起完成。 相似三角形的性质
性质:
……………… 1、证明:
………………
……………… 2、证明:
……………… 主要板书设计呈现主要内容,梳理知识结构。
