浙江省绍兴市柯桥区2023-2024学年九年级上学期期末数学试题(含答案)
文档属性
| 名称 | 浙江省绍兴市柯桥区2023-2024学年九年级上学期期末数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 16:34:24 | ||
图片预览




文档简介
2024年柯桥区初三分层走班分类评价
数学试卷
考生须知:
1.全卷分试卷和答题卷二部分,考生须在答题卷上作答,全卷满分120分,考试时间120分钟.
2.试卷分试卷Ⅰ(选择题),试卷Ⅱ(非选择题)两部分,共8页.
试卷Ⅰ(选择题,共30分)
请将本卷的答案,用铅笔在答题纸上对应的选项位置涂黑、涂满
一、选择题(本题有10小题,每小题3分,共30分)
1.若,则的值为( )
A. B. C.4 D.
2.已知点与在同一平面内,的半径为6,若,则点与的位置关系是( )
A.点在圆内 B.点在圆上 C.点在圆外 D.点在圆上或圆外
3.在一个不透明的袋子里装有2个白球和3个红球,它们除颜色外其余都相同,从中任意摸出1个球,则摸出的球为白球的概率是( )
A. B. C. D.
4.把二次函数的图象向左平移3个单位,向上平移4个单位后,得到的图象所对应的二次函数表达式为( )
A. B.
C. D.
5.为制作风筝,小明做了如图所示的风筝支架示意图,已知点、点分别在射线与上,且,则的长是( )
(第5题图)
A. B. C. D.
6.如图是一段圆弧,点是这段弧所在圆的圆心,为上一点,于点.若,则的长为( )
(第6题图)
A. B. C. D.
7.二次函数的图象经过点,则,的大小关系正确的为( )
A. B. C. D.
8.如图,某公园为了使残疾人的轮椅行走方便,设想拆除台阶换成斜坡,又考虑安全,斜坡的坡角不得超过,此公园门前的台阶高出地面1.62米,则斜坡的水平宽度至少需( )(精确到0.1米.参考值:)
(第8题图)
A.9.1米 B.9.5米 C.9.4米 D.9.0米
9.已知二次函数图象上部分点的坐标的对应值如表所示:
… 0 6 …
… 0.39 0.39 …
则方程的解是( )
A.0或6 B.或 C.或6 D.无实数解
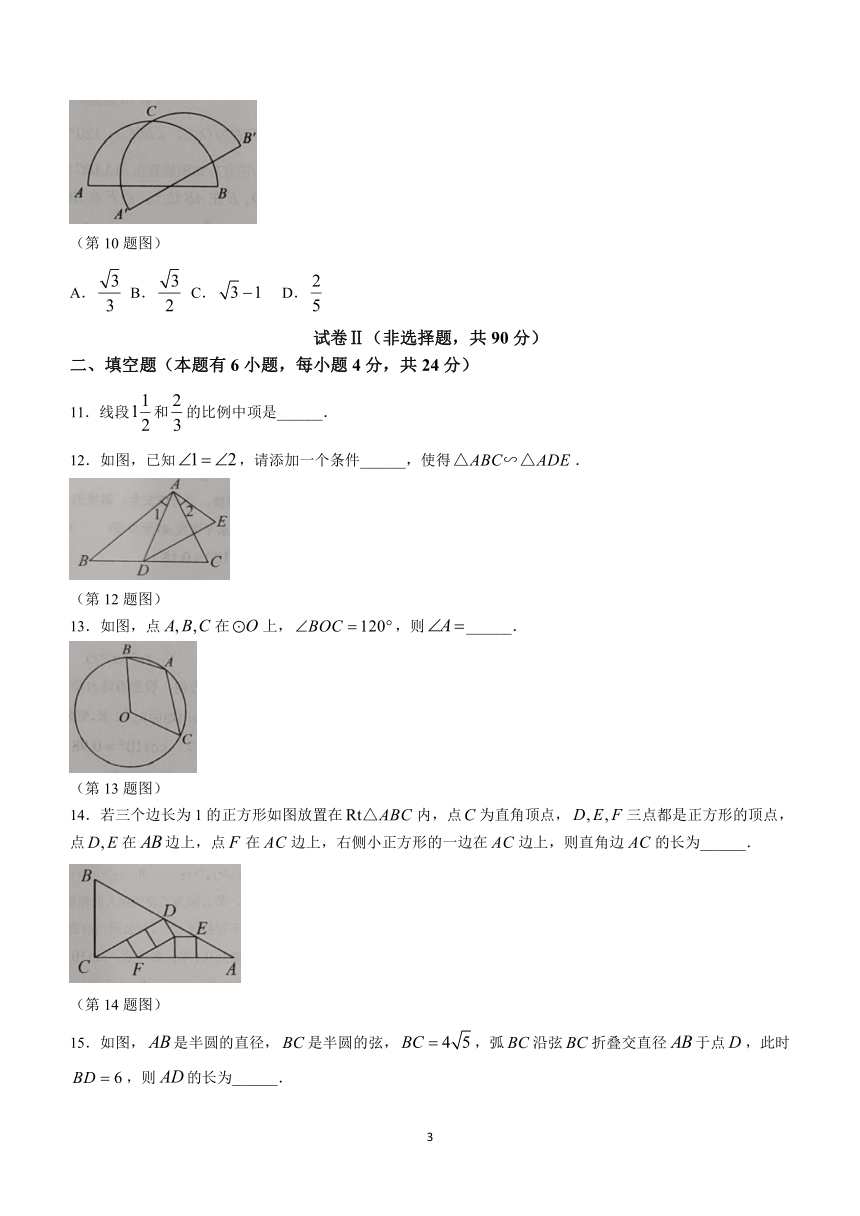
10.如图,以为直径作半圆弧,为半圆弧的中点,现将半圆连同直径绕点逆时针旋转,记点的对应点分别为,连结,则( )
(第10题图)
A. B. C. D.
试卷Ⅱ(非选择题,共90分)
二、填空题(本题有6小题,每小题4分,共24分)
11.线段和的比例中项是______.
12.如图,已知,请添加一个条件______,使得.
(第12题图)
13.如图,点在上,,则______.
(第13题图)
14.若三个边长为1的正方形如图放置在内,点为直角顶点,三点都是正方形的顶点,点在边上,点在边上,右侧小正方形的一边在边上,则直角边的长为______.
(第14题图)
15.如图,是半圆的直径,是半圆的弦,,弧沿弦折叠交直径于点,此时,则的长为______.
(第15题图)
16.如图,为平面直角坐标的原点,直线与两坐标轴交于两点,,,若的圆心在直线上,且与所在直线相切,则圆心的坐标是______.
(第16题图)
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.计算:.
18.为响应国家“双减”政策,大力推行课后服务,丰富学生课后生活,某校开设A班剪纸、B班戏曲、C班武术、D班围棋四门特色课程,甲、乙两位同学各需选择一门课程学习.
(1)求甲同学选择A班剪纸课的概率.
(2)利用树状图或列表法,求甲、乙两人选择同一门课程的概率.
19.如图,在平面直角坐标系中,已知的三个顶点分别是,.
(第19题图)
(1)请画出将绕点顺时针旋转后得到的.
(2)在(1)的条件下,求扇形的面积(结果保留).
20.绍兴大善塔“风韵独秀”,为测得大善塔的高度,某校数学社团开展实践活动.他们利用无人机在塔树连线的正上方处悬停,在同一平面内,,点在一条直线上,为的中点,米,测得塔顶的俯角为37°,树顶的俯角为60°,树高为11米,求塔高的值.(参考数据:,)
(第20题图)
21.已知二次函数
(1)若二次函数图象与轴交于点.求二次函数的表达式.
(2)当时,的最小值为,求的值.
22.如图,为圆的直径,点为的中点,连结,过点作,交的延长线于点.
(第22题图)
(1)求证:是圆的切线.
(2)延长交的延长线于点,若,求直径的长.
23.利用素材解决:《桥梁的设计》
问题驱动 某地欲修建一座拱桥,桥的底部两端间的水面宽,称跨度,桥面最高点到的距离称拱高,拱桥的轮廓可以设计成是圆弧型或抛物线型,若修建拱桥的跨度米,拱高米.
设计方案 方案一 方案二
设计类型 圆弧型 抛物线型
任务一 设计成圆弧型,求该圆弧所在圆的半径. 设计成抛物线型,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,求桥拱的函数表达式.
任务二 如图,一艘货船露出水面部分的横截面为矩形,测得米,米.请你通过计算说明货船能否分别顺利通过这两座桥梁.
24.如图,圆的弦,点为圆外一点,连结分别交圆于点,点,,连结
图1 图2
(1)如图1,若圆的半径5,,求的长;
(2)如图2,若
①求的值;
②求圆的半径.
2023学年第一学期九年级期终学业评价调测试卷答案及评分标准
总分:120分
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C A D B D D B A
二、填空题(每小题4分,共24分)
11.1 12.或或 13.120° 14. 15.4 16.或
三、解答题(共66分)
17.解:原式.
18.解:(1)甲同学选择A班剪纸课的概率是.
(2)画树状图如下:
共有16种等可能的结果,其中甲,乙两人选同一门课程的结果有4种,
∴甲和乙选择同一个课程的概率为.
19.解:(1)图略
(2).
∴.
20.解:如图:延长交于点,延长交于点,
为的中点,,
由题意得:,
在中,.,
,
在中,,,
(米)
塔高的值为40.4米.
21.解:(1)把代入解析式,得,
二次函数的解析式为.
(2)当时,当有最小值,把代入得
当时,当有最小值.把代入得
或.
22.解:(1)连接为的中点,
,即.
.
,
,即是的切线.
(2)连接,
,,
.
,,,即是直径的长5.
23.解:任务一
方案一,设圆的半径为米,在中,,
(米)
方案二,∵顶点C坐标为,设桥拱的函数解析式为
代入得,.
函数解析式为.
任务二
方案一,如图,由上得,
在中,.
能通过.(判断高度也可)
方案二,如图建立直角坐标系,
当H点的横坐标时,,
不能通过.
24.(1)连结为直径10.
,在中,.
(2)①∵四边形内接于圆,
,
②过作交圆于点,连结
弧弧为正三角形
过作
数学试卷
考生须知:
1.全卷分试卷和答题卷二部分,考生须在答题卷上作答,全卷满分120分,考试时间120分钟.
2.试卷分试卷Ⅰ(选择题),试卷Ⅱ(非选择题)两部分,共8页.
试卷Ⅰ(选择题,共30分)
请将本卷的答案,用铅笔在答题纸上对应的选项位置涂黑、涂满
一、选择题(本题有10小题,每小题3分,共30分)
1.若,则的值为( )
A. B. C.4 D.
2.已知点与在同一平面内,的半径为6,若,则点与的位置关系是( )
A.点在圆内 B.点在圆上 C.点在圆外 D.点在圆上或圆外
3.在一个不透明的袋子里装有2个白球和3个红球,它们除颜色外其余都相同,从中任意摸出1个球,则摸出的球为白球的概率是( )
A. B. C. D.
4.把二次函数的图象向左平移3个单位,向上平移4个单位后,得到的图象所对应的二次函数表达式为( )
A. B.
C. D.
5.为制作风筝,小明做了如图所示的风筝支架示意图,已知点、点分别在射线与上,且,则的长是( )
(第5题图)
A. B. C. D.
6.如图是一段圆弧,点是这段弧所在圆的圆心,为上一点,于点.若,则的长为( )
(第6题图)
A. B. C. D.
7.二次函数的图象经过点,则,的大小关系正确的为( )
A. B. C. D.
8.如图,某公园为了使残疾人的轮椅行走方便,设想拆除台阶换成斜坡,又考虑安全,斜坡的坡角不得超过,此公园门前的台阶高出地面1.62米,则斜坡的水平宽度至少需( )(精确到0.1米.参考值:)
(第8题图)
A.9.1米 B.9.5米 C.9.4米 D.9.0米
9.已知二次函数图象上部分点的坐标的对应值如表所示:
… 0 6 …
… 0.39 0.39 …
则方程的解是( )
A.0或6 B.或 C.或6 D.无实数解
10.如图,以为直径作半圆弧,为半圆弧的中点,现将半圆连同直径绕点逆时针旋转,记点的对应点分别为,连结,则( )
(第10题图)
A. B. C. D.
试卷Ⅱ(非选择题,共90分)
二、填空题(本题有6小题,每小题4分,共24分)
11.线段和的比例中项是______.
12.如图,已知,请添加一个条件______,使得.
(第12题图)
13.如图,点在上,,则______.
(第13题图)
14.若三个边长为1的正方形如图放置在内,点为直角顶点,三点都是正方形的顶点,点在边上,点在边上,右侧小正方形的一边在边上,则直角边的长为______.
(第14题图)
15.如图,是半圆的直径,是半圆的弦,,弧沿弦折叠交直径于点,此时,则的长为______.
(第15题图)
16.如图,为平面直角坐标的原点,直线与两坐标轴交于两点,,,若的圆心在直线上,且与所在直线相切,则圆心的坐标是______.
(第16题图)
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.计算:.
18.为响应国家“双减”政策,大力推行课后服务,丰富学生课后生活,某校开设A班剪纸、B班戏曲、C班武术、D班围棋四门特色课程,甲、乙两位同学各需选择一门课程学习.
(1)求甲同学选择A班剪纸课的概率.
(2)利用树状图或列表法,求甲、乙两人选择同一门课程的概率.
19.如图,在平面直角坐标系中,已知的三个顶点分别是,.
(第19题图)
(1)请画出将绕点顺时针旋转后得到的.
(2)在(1)的条件下,求扇形的面积(结果保留).
20.绍兴大善塔“风韵独秀”,为测得大善塔的高度,某校数学社团开展实践活动.他们利用无人机在塔树连线的正上方处悬停,在同一平面内,,点在一条直线上,为的中点,米,测得塔顶的俯角为37°,树顶的俯角为60°,树高为11米,求塔高的值.(参考数据:,)
(第20题图)
21.已知二次函数
(1)若二次函数图象与轴交于点.求二次函数的表达式.
(2)当时,的最小值为,求的值.
22.如图,为圆的直径,点为的中点,连结,过点作,交的延长线于点.
(第22题图)
(1)求证:是圆的切线.
(2)延长交的延长线于点,若,求直径的长.
23.利用素材解决:《桥梁的设计》
问题驱动 某地欲修建一座拱桥,桥的底部两端间的水面宽,称跨度,桥面最高点到的距离称拱高,拱桥的轮廓可以设计成是圆弧型或抛物线型,若修建拱桥的跨度米,拱高米.
设计方案 方案一 方案二
设计类型 圆弧型 抛物线型
任务一 设计成圆弧型,求该圆弧所在圆的半径. 设计成抛物线型,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,求桥拱的函数表达式.
任务二 如图,一艘货船露出水面部分的横截面为矩形,测得米,米.请你通过计算说明货船能否分别顺利通过这两座桥梁.
24.如图,圆的弦,点为圆外一点,连结分别交圆于点,点,,连结
图1 图2
(1)如图1,若圆的半径5,,求的长;
(2)如图2,若
①求的值;
②求圆的半径.
2023学年第一学期九年级期终学业评价调测试卷答案及评分标准
总分:120分
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C A D B D D B A
二、填空题(每小题4分,共24分)
11.1 12.或或 13.120° 14. 15.4 16.或
三、解答题(共66分)
17.解:原式.
18.解:(1)甲同学选择A班剪纸课的概率是.
(2)画树状图如下:
共有16种等可能的结果,其中甲,乙两人选同一门课程的结果有4种,
∴甲和乙选择同一个课程的概率为.
19.解:(1)图略
(2).
∴.
20.解:如图:延长交于点,延长交于点,
为的中点,,
由题意得:,
在中,.,
,
在中,,,
(米)
塔高的值为40.4米.
21.解:(1)把代入解析式,得,
二次函数的解析式为.
(2)当时,当有最小值,把代入得
当时,当有最小值.把代入得
或.
22.解:(1)连接为的中点,
,即.
.
,
,即是的切线.
(2)连接,
,,
.
,,,即是直径的长5.
23.解:任务一
方案一,设圆的半径为米,在中,,
(米)
方案二,∵顶点C坐标为,设桥拱的函数解析式为
代入得,.
函数解析式为.
任务二
方案一,如图,由上得,
在中,.
能通过.(判断高度也可)
方案二,如图建立直角坐标系,
当H点的横坐标时,,
不能通过.
24.(1)连结为直径10.
,在中,.
(2)①∵四边形内接于圆,
,
②过作交圆于点,连结
弧弧为正三角形
过作
同课章节目录
