浙江省台州市玉环市2023-2024学年九年级上学期期末数学试题(无答案)
文档属性
| 名称 | 浙江省台州市玉环市2023-2024学年九年级上学期期末数学试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 365.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 16:35:31 | ||
图片预览


文档简介
玉环市2023学年第一学期期末检测试卷
九年级数学
亲爱的同学:
欢迎参加本次考试!请认真审题,仔细解答,发挥最佳水平。答题时请注意以下几点:
1.试卷共4页,答题纸4页,满分120分,考试时间120分钟;
2.答案必须写在答题纸相应的位置上,写在试卷、草稿纸上无效;
3.本次考试不得使用计算器,请耐心解答。祝你成功!
一、选择题(本题有10小题,每小题3分,共30分,每小题有且只有一个选项是正确的,不选、多选、错选均不给分)
1.下列是四款新能源汽车的标志,其中是中心对称图形的是( )
A. B. C. D.
2.下列事件为必然事件的是( )
A.掷一枚均匀的骰子,朝上的面点数为偶数
B.某射击运动员射靶一次,正中靶心
C.打开电视,正在播广告
D.口袋中仅装有3个红球,从中摸出1个球,必是红球
3.如图,点A、B、C在⊙O上,若∠C=38°,则∠AOB的度数为( )
第3题图
A.38° B.76° C.80° D.60°
4.已知,,DE=9,则EF=( )
第4题图
A.12 B.15 C.28 D.24
5.抛物线的顶点坐标是( )
A.(0,-4) B.(-4,0) C.(4,0) D.(0,4)
6.已知⊙O的半径为3,当OP=5时,点P与⊙O的位置关系为( )
A.点在圆内 B.点在圆外 C.点在圆上 D.不能确定
7.如图,将正方形ABCD绕着点A逆时针旋转得到正方形AEFG,点B的对应点E落在正方形ABCD的对角线AC上,若AD=1,则的长为( )
第7题图
A. B. C. D.
8.若点,,在反比例函数的图象上,则,,大小关系是( )
A. B. C. D.
9.我们把顶角为36°的等腰三角形称为“黄金三角形”,它的底与腰的比值为黄金比.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,若CD=1,则AC的长为( )
第9题图
A. B. C. D.
10.已知二次函数,当时,函数的最大值与最小值的差为3,则a的值为( )
A.1或0 B.1或 C.或 D.0或
二、填空题(本题有6小题,每小题4分,共24分)
11.已知反比例函数的图象经过点(-3,m),则m的值为______.
12.在一个不透明盒子里,装有若干个红色、白色的小球(除了颜色外均相同),将球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复.下表是一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到红球的次数m 59 96 116 295 480 601
摸到红球的频率 0.59 0.64 0.58 0.59 0.60 0.601
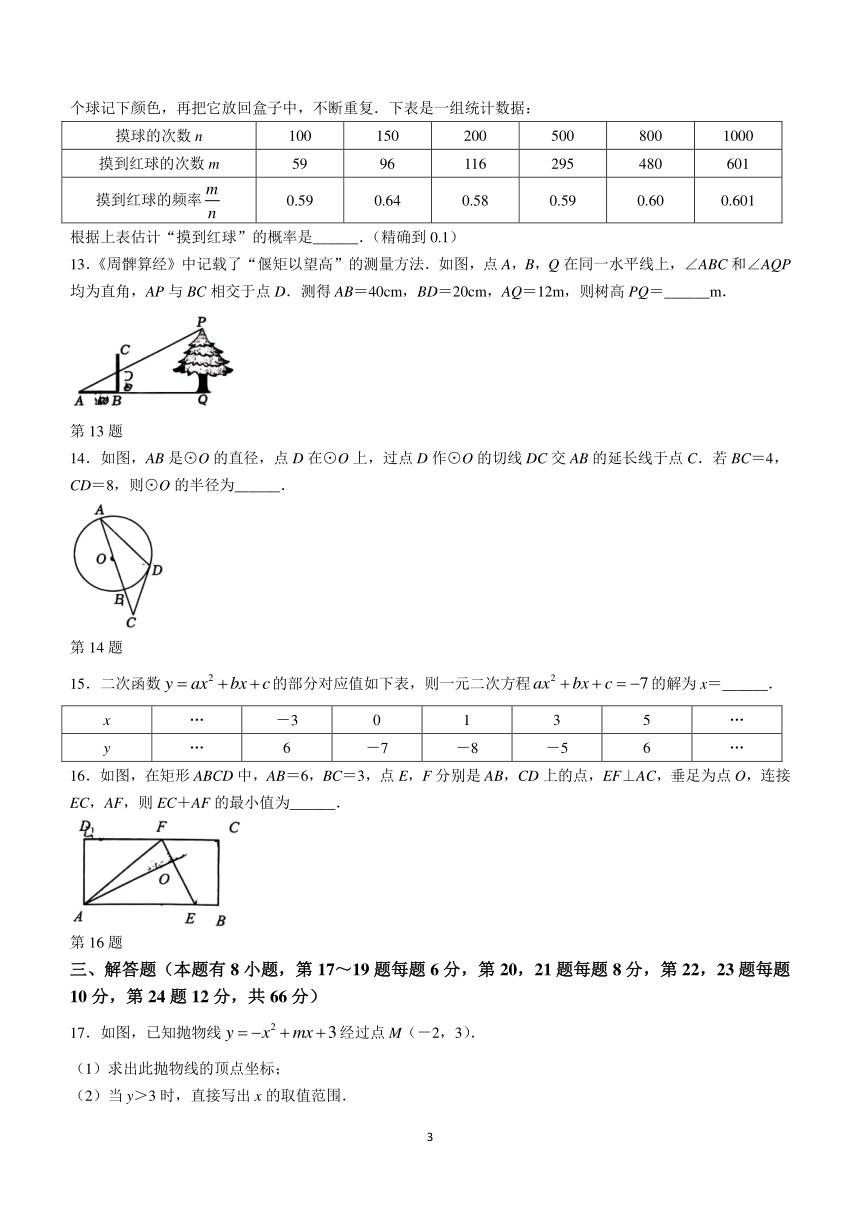
根据上表估计“摸到红球”的概率是______.(精确到0.1)
13.《周髀算经》中记载了“偃矩以望高”的测量方法.如图,点A,B,Q在同一水平线上,∠ABC和∠AQP均为直角,AP与BC相交于点D.测得AB=40cm,BD=20cm,AQ=12m,则树高PQ=______m.
第13题
14.如图,AB是⊙O的直径,点D在⊙O上,过点D作⊙O的切线DC交AB的延长线于点C.若BC=4,CD=8,则⊙O的半径为______.
第14题
15.二次函数的部分对应值如下表,则一元二次方程的解为x=______.
x … -3 0 1 3 5 …
y … 6 -7 -8 -5 6 …
16.如图,在矩形ABCD中,AB=6,BC=3,点E,F分别是AB,CD上的点,EF⊥AC,垂足为点O,连接EC,AF,则EC+AF的最小值为______.
第16题
三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)
17.如图,已知抛物线经过点M(-2,3).
(1)求出此抛物线的顶点坐标;
(2)当y>3时,直接写出x的取值范围.
第17题图
18.在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)画出△ABC关于点O的中心对称图形;
(2)将△ABC绕着点O逆时针旋转90°,画出旋转后得到的;并直接写出点,的坐标.
第18题图
19.浙江省餐饮行业协会共同评定产生全省“味美浙江·百县千碗”1000道风味美食名录,玉环有多道美食上榜.例如“明炉望潮”“敲鱼三鲜”“干蒸白蟹”“东海鱼冻”等.
(1)小明想从以上这4道美食中随机选择1道品尝,则他选中“东海鱼冻”的概率为______;
(2)某中学拟从这4道美食中选择2道作为美食节特色菜肴,若用A,B,C,D分别表示“明炉望潮”“敲鱼三鲜”“干蒸白蟹”“东海鱼冻”,请用画树状图或列表的方法求出恰好选中“明炉望潮”“敲鱼三鲜”的概率.
20.如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
(1)求证:BE=CF;
(2)求∠BDC的度数.
第20题
21.你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)x()的反比例函数,其图象如图所示.
(1)求当面条粗时,面条的总长度是多少米?
(2)若面条的总长度要求不大于50m,那面条的粗细有什么限制?
第21题图
22.如图,在△ABC中,BC=3,D为AC延长线上一点,AC=3CD,∠CBD=∠A,过D作DH∥AB,交BC的延长线于点H.
(1)求证:△HCD∽△HDB.
(2)求DH长度.
第22题图
23.某游乐场将修建一款大型过山车.下图为这款过山车的一部分轨道设计图,OA为笔直轨道,A→B→C为第一段抛物线轨道,C→D→E为第二段抛物线轨道(接口处轨道忽略不计B,D为均为抛物线顶点),C,E,F在同一直线上且平行于地面,CE为22米,若以点O为原点,地面水平线为x轴,O点竖直方向为y轴,以1米为一个单位长度,建立如图所示的平面直角坐标系,其中点A为(35,40),点B为(50,17.5)
(1)设第一段抛物线轨道函数解析式为,请求出该函数解析式;
(2)设计规定点C离地距离需在25.6到27.5米之间(含25.6米和27.5米),请求出点C横坐标的范围;
(3)在(1)(2)的基础上,C取最高点,已知第二段抛物线轨道函数为,为保证安全,抛物线轨道最低点不低于5米,请确认第二段抛物线轨道是否符合要求,并说明理由.
第23题图
24.已知△ABC为等腰直角三角形,∠BAC=90°,D是射线CA上一点,以BD为直径的⊙O交BC于点E,过A作AF∥BC交⊙O于点F,连接FB,连接DF.
(1)如图1,当D在线段CA上时
①求证:△BDF是等腰直角三角形;
②若D为AC中点,求的值;
(2)连接CF,若AD=1,CD=3,求CF的长.
第24题图
九年级数学
亲爱的同学:
欢迎参加本次考试!请认真审题,仔细解答,发挥最佳水平。答题时请注意以下几点:
1.试卷共4页,答题纸4页,满分120分,考试时间120分钟;
2.答案必须写在答题纸相应的位置上,写在试卷、草稿纸上无效;
3.本次考试不得使用计算器,请耐心解答。祝你成功!
一、选择题(本题有10小题,每小题3分,共30分,每小题有且只有一个选项是正确的,不选、多选、错选均不给分)
1.下列是四款新能源汽车的标志,其中是中心对称图形的是( )
A. B. C. D.
2.下列事件为必然事件的是( )
A.掷一枚均匀的骰子,朝上的面点数为偶数
B.某射击运动员射靶一次,正中靶心
C.打开电视,正在播广告
D.口袋中仅装有3个红球,从中摸出1个球,必是红球
3.如图,点A、B、C在⊙O上,若∠C=38°,则∠AOB的度数为( )
第3题图
A.38° B.76° C.80° D.60°
4.已知,,DE=9,则EF=( )
第4题图
A.12 B.15 C.28 D.24
5.抛物线的顶点坐标是( )
A.(0,-4) B.(-4,0) C.(4,0) D.(0,4)
6.已知⊙O的半径为3,当OP=5时,点P与⊙O的位置关系为( )
A.点在圆内 B.点在圆外 C.点在圆上 D.不能确定
7.如图,将正方形ABCD绕着点A逆时针旋转得到正方形AEFG,点B的对应点E落在正方形ABCD的对角线AC上,若AD=1,则的长为( )
第7题图
A. B. C. D.
8.若点,,在反比例函数的图象上,则,,大小关系是( )
A. B. C. D.
9.我们把顶角为36°的等腰三角形称为“黄金三角形”,它的底与腰的比值为黄金比.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,若CD=1,则AC的长为( )
第9题图
A. B. C. D.
10.已知二次函数,当时,函数的最大值与最小值的差为3,则a的值为( )
A.1或0 B.1或 C.或 D.0或
二、填空题(本题有6小题,每小题4分,共24分)
11.已知反比例函数的图象经过点(-3,m),则m的值为______.
12.在一个不透明盒子里,装有若干个红色、白色的小球(除了颜色外均相同),将球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复.下表是一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到红球的次数m 59 96 116 295 480 601
摸到红球的频率 0.59 0.64 0.58 0.59 0.60 0.601
根据上表估计“摸到红球”的概率是______.(精确到0.1)
13.《周髀算经》中记载了“偃矩以望高”的测量方法.如图,点A,B,Q在同一水平线上,∠ABC和∠AQP均为直角,AP与BC相交于点D.测得AB=40cm,BD=20cm,AQ=12m,则树高PQ=______m.
第13题
14.如图,AB是⊙O的直径,点D在⊙O上,过点D作⊙O的切线DC交AB的延长线于点C.若BC=4,CD=8,则⊙O的半径为______.
第14题
15.二次函数的部分对应值如下表,则一元二次方程的解为x=______.
x … -3 0 1 3 5 …
y … 6 -7 -8 -5 6 …
16.如图,在矩形ABCD中,AB=6,BC=3,点E,F分别是AB,CD上的点,EF⊥AC,垂足为点O,连接EC,AF,则EC+AF的最小值为______.
第16题
三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)
17.如图,已知抛物线经过点M(-2,3).
(1)求出此抛物线的顶点坐标;
(2)当y>3时,直接写出x的取值范围.
第17题图
18.在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)画出△ABC关于点O的中心对称图形;
(2)将△ABC绕着点O逆时针旋转90°,画出旋转后得到的;并直接写出点,的坐标.
第18题图
19.浙江省餐饮行业协会共同评定产生全省“味美浙江·百县千碗”1000道风味美食名录,玉环有多道美食上榜.例如“明炉望潮”“敲鱼三鲜”“干蒸白蟹”“东海鱼冻”等.
(1)小明想从以上这4道美食中随机选择1道品尝,则他选中“东海鱼冻”的概率为______;
(2)某中学拟从这4道美食中选择2道作为美食节特色菜肴,若用A,B,C,D分别表示“明炉望潮”“敲鱼三鲜”“干蒸白蟹”“东海鱼冻”,请用画树状图或列表的方法求出恰好选中“明炉望潮”“敲鱼三鲜”的概率.
20.如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
(1)求证:BE=CF;
(2)求∠BDC的度数.
第20题
21.你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)x()的反比例函数,其图象如图所示.
(1)求当面条粗时,面条的总长度是多少米?
(2)若面条的总长度要求不大于50m,那面条的粗细有什么限制?
第21题图
22.如图,在△ABC中,BC=3,D为AC延长线上一点,AC=3CD,∠CBD=∠A,过D作DH∥AB,交BC的延长线于点H.
(1)求证:△HCD∽△HDB.
(2)求DH长度.
第22题图
23.某游乐场将修建一款大型过山车.下图为这款过山车的一部分轨道设计图,OA为笔直轨道,A→B→C为第一段抛物线轨道,C→D→E为第二段抛物线轨道(接口处轨道忽略不计B,D为均为抛物线顶点),C,E,F在同一直线上且平行于地面,CE为22米,若以点O为原点,地面水平线为x轴,O点竖直方向为y轴,以1米为一个单位长度,建立如图所示的平面直角坐标系,其中点A为(35,40),点B为(50,17.5)
(1)设第一段抛物线轨道函数解析式为,请求出该函数解析式;
(2)设计规定点C离地距离需在25.6到27.5米之间(含25.6米和27.5米),请求出点C横坐标的范围;
(3)在(1)(2)的基础上,C取最高点,已知第二段抛物线轨道函数为,为保证安全,抛物线轨道最低点不低于5米,请确认第二段抛物线轨道是否符合要求,并说明理由.
第23题图
24.已知△ABC为等腰直角三角形,∠BAC=90°,D是射线CA上一点,以BD为直径的⊙O交BC于点E,过A作AF∥BC交⊙O于点F,连接FB,连接DF.
(1)如图1,当D在线段CA上时
①求证:△BDF是等腰直角三角形;
②若D为AC中点,求的值;
(2)连接CF,若AD=1,CD=3,求CF的长.
第24题图
同课章节目录
