第三单元_第03课时++减法性质的简便计算+(教学课件)-四年级数学下册人教版 (2)(共30张PPT)
文档属性
| 名称 | 第三单元_第03课时++减法性质的简便计算+(教学课件)-四年级数学下册人教版 (2)(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 16:21:22 | ||
图片预览









文档简介
(共30张PPT)
第2课时 加法运算定律
的应用
小学数学·四年级(下)·RJ
在解决问题的过程中,体现策略的多样化,提高灵活、合理选择算法的能力。
通过学习,能正确、自主地运用加法交换律和结合律进行简便计算。
培养学生独立思考和主动探究的意识和习惯。
能正确运用加法交换律和结合律进行简便计算。
根据数据特点,灵活、合理地选择计算方法。
训练学生思维严谨、书写规范,养成良好的数学思维习惯。
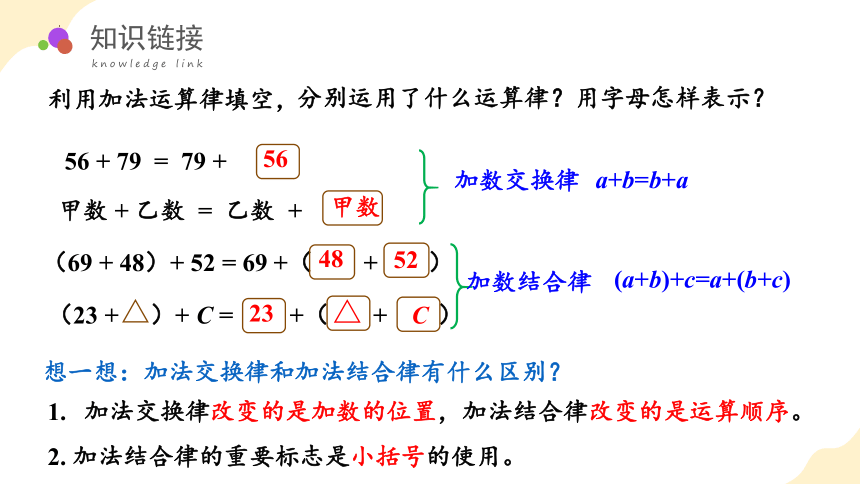
(69 + 48)+ 52 = 69 +( + )
利用加法运算律填空,
56
甲数
48
52
56 + 79 = 79 +
甲数 + 乙数 = 乙数 +
(23 + )+ C = +( + )
23
C
分别运用了什么运算律?用字母怎样表示?
加数交换律
a+b=b+a
加数结合律
(a+b)+c=a+(b+c)
想一想:加法交换律和加法结合律有什么区别?
加法交换律改变的是加数的位置,加法结合律改变的是运算顺序。
2. 加法结合律的重要标志是小括号的使用。
口算大比拼。
74+26=
85+77=
76+28=
59+67=
25+35=
42+28=
126
162
104
60
100
70
右边的算式中两个数合起来是整十数、整百数。
观察左右两边的算式,说一说你有什么发现?
探究例3的解决方法
下面是李叔叔后四天的行程计划。
按照计划,李叔叔后四天还要骑行多少千米?
说一说从题中你了解到哪些数学信息 需要解决什么问题
已知:第四天骑行115km
第五天骑行132km
第六天骑行118km
第七天骑行85km
求:四天骑行的总路程是多少千米
阅读与理解
第四天 第五天 第六天 第七天
A→B B→C C→D D→E
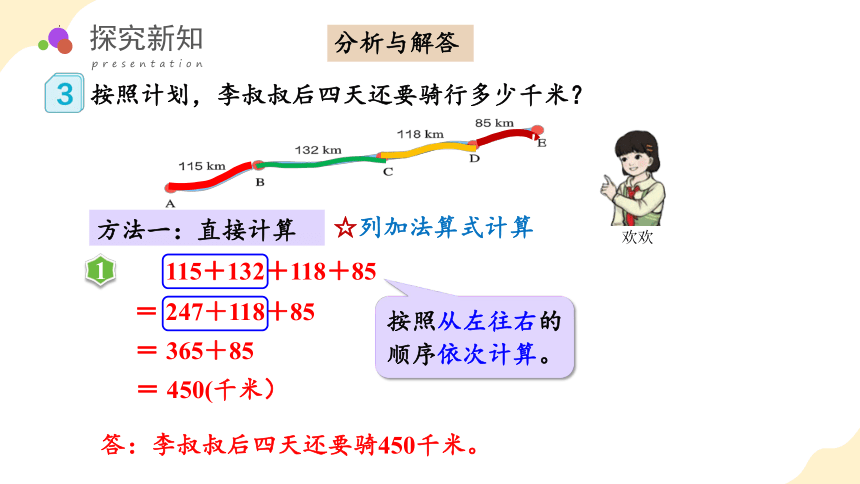
按照计划,李叔叔后四天还要骑行多少千米?
方法一:直接计算
☆列加法算式计算
1
115+132+118+85
答:李叔叔后四天还要骑450千米。
= 247+118+85
= 365+85
= 450(千米)
按照从左往右的顺序依次计算。
分析与解答
欢欢
2
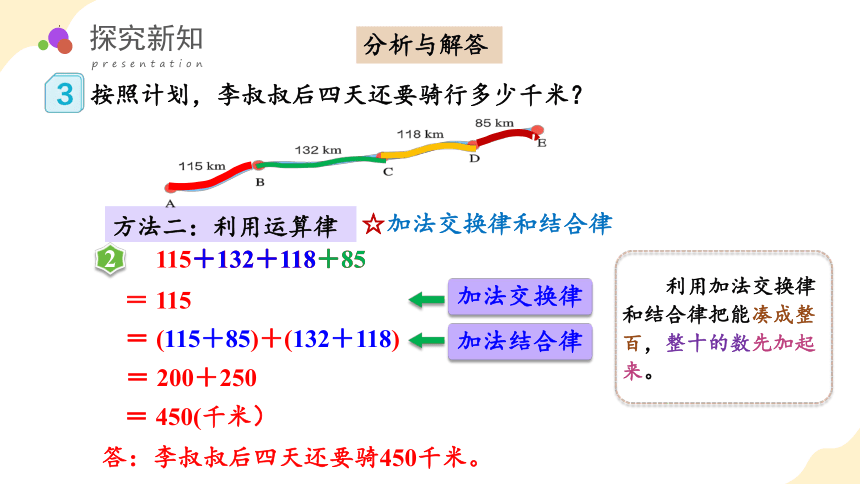
115+132+118+85
答:李叔叔后四天还要骑450千米。
= 115
= (115+85)+(132+118)
= 200+250
加法交换律
加法结合律
= 450(千米)
+85
+132+118
利用加法交换律和结合律把能凑成整百,整十的数先加起来。
方法二:利用运算律
☆加法交换律和结合律
分析与解答
按照计划,李叔叔后四天还要骑行多少千米?
比较例3的两种方法
115+132+118+85
=85+115+132+118
=(85+115)+(132+118)
=200+250
=450
方法一
115+132+118+85
=247+118+85
=365+85
=450
观察几个连加的加数的特点,想一想:怎样让运算变得简单?
利用加法交换律和结合律把能凑成整十,整百或整千的数结合在一起先加起来,可以使计算简便。
方法二
比一比:哪种方法更简便
想一想,说一说:在刚才运用加法运算律计算过程中,有哪些注意的?
加法简便计算的方法
一看
运算符号
数字特点
二想
凑整 运算定律
三算
准确计算
连加算式仔细算,
运算定律记心间。
整十、整百和整千,
结合先算更简便。
反思与总结
更深入地理解了加法交换律和加法结合律。
先整体观察算式,根据数据特点进行凑整……
解决问题时要有理有据……
通过今天的学习,你有什么收获?
反思与总结
扩展延伸-高斯求和
同学们,你们听说过数学家高斯小时候计算:1+2+3+···+100
的和是多少的故事吗?
(1) 1+2+3+4+…+98+99+100
这几组配对的数的和都为101
100个数共可配100÷2=50(组)
1+2+3+4+···+98+99+100
=101×50
=5050
1+100=101
2+99=101
3+98=101
4+97=101
……
49+52=101
50+51=101
共50个101
* 用合适的方法计算。
教材第23 练习六 第9题
(2)2+4+6+…+16+18+20
这几组配对的数的和都为22
10个数共可配10÷2=5(组)
2+4+6+…+16+18+20
=(2+20) +(4+18) +(6+16)+(8+14) +(10+12)
=22×5
=110
* 用合适的方法计算。
教材第23 练习六 第9题
(3)5+10+15+…+90+95+100
这几组配对的数的和都为105
20个数共可配20÷2=10(组)
5+10+15+…+90+95+100
=105×10
=1050
* 用合适的方法计算。
教材第23 练习六 第9题
(4)20 19+18 17+…+4 3+2 1
1
1
1
1
一共20个数,则有10个1
20 19+18 17+…+4 3+2 1
=(20 19)+(18 17)+…+(4 3) +(2 1)
=1+1+…+1+1
=1×10
=10
* 用合适的方法计算。
解题关键:先观察算式中数据的特点,若算式中数据两两结合可以凑成某个相同的数,可利用分组法将数据两两结合再进行计算。分组时注意一共分成了多少组,有没有数据遗漏。
说一说解决此类问题的关键是什么?
教材第23 练习六 第9题
达标练习,巩固成果
计算下面各题,怎样简便就怎样计算。
425 + 14 + 186 75 + 168 + 25
= 425+(14+186)
= 425+200
= 625
14 + 186
75
+ 25
+ 168
=
= 100+168
= 268
245 + 180 + 20 + 155 67 + 25 + 33 + 75
=
= (245+155)+(180+20)
= 400 +200
= 600
245
+ 155
+ 180 + 20
=
+ 25
+ 75
+ 33
67
= 100 +100
= 200
= (67+33)+(25+75)
教材第20页“做一做”第1题
1
刘老师购买了下列体育用品,一共花了多少钱?
48+55+52+45
=(48+52)+(55+45)
= 100+100
= 200(元)
答:一共花了200元钱。
48元 55元 52元 45元
教材第20页“做一做”第2题
2
225+328+175
=225+175+328
=400+328
=728(元)
答:王阿姨一共收到转账款728元。
3月6日—11日王阿姨共收到转账款多少元?
3
教材第22 练习六 第2题
这堆原木一共多少根?
1根
2根
3根
……
一层一层记下根数
1+2+3+4+5+6+7+8+9+10
= (1+9)+(2+8)+(3+7)+(4+6)+5+10
= 10+10+10+10+5+10
= 10×5+5
= 50+5
= 55(根)
答:这堆原木一共有55根。
原木总数等于每一层原木的根数相加的和。
方法一
4
教材第22 练习六 第4题
这堆原木一共多少根?
1+2+3+4+5+6+7+8+9+10
=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)
=11+11+11+11+11
=11 × 5
=55(根)
答:这堆原木一共有55根。
方法二
4
教材第22 练习六 第4题
2255+355+245
=2255+(355+245)
=2255+600
=2855(元) 答:这台彩电原价2855元。
这台电视机原价多少钱?
彩电原价等于现价加两次降价。
5
教材第23 练习六 第7题
先思考,再计算,怎样简便怎样算。
9 + 99 + 999 + 9999
= (1+1+1+6) +99+999 +9999
= (1+99) + (1+999) + (1+9999)+6
= 100+1000+10000+6
= 11106
比一比,看谁的方法更简便!
9
6
加法运算定律的应用
1. 合理运用加法运算定律可以简便运算。
2. 简算的核心是“凑整”或“相同的数”。
3. 看哪两个数相加能凑成整十、整百或整千,
或相同的数。
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
第2课时 加法运算定律
的应用
小学数学·四年级(下)·RJ
在解决问题的过程中,体现策略的多样化,提高灵活、合理选择算法的能力。
通过学习,能正确、自主地运用加法交换律和结合律进行简便计算。
培养学生独立思考和主动探究的意识和习惯。
能正确运用加法交换律和结合律进行简便计算。
根据数据特点,灵活、合理地选择计算方法。
训练学生思维严谨、书写规范,养成良好的数学思维习惯。
(69 + 48)+ 52 = 69 +( + )
利用加法运算律填空,
56
甲数
48
52
56 + 79 = 79 +
甲数 + 乙数 = 乙数 +
(23 + )+ C = +( + )
23
C
分别运用了什么运算律?用字母怎样表示?
加数交换律
a+b=b+a
加数结合律
(a+b)+c=a+(b+c)
想一想:加法交换律和加法结合律有什么区别?
加法交换律改变的是加数的位置,加法结合律改变的是运算顺序。
2. 加法结合律的重要标志是小括号的使用。
口算大比拼。
74+26=
85+77=
76+28=
59+67=
25+35=
42+28=
126
162
104
60
100
70
右边的算式中两个数合起来是整十数、整百数。
观察左右两边的算式,说一说你有什么发现?
探究例3的解决方法
下面是李叔叔后四天的行程计划。
按照计划,李叔叔后四天还要骑行多少千米?
说一说从题中你了解到哪些数学信息 需要解决什么问题
已知:第四天骑行115km
第五天骑行132km
第六天骑行118km
第七天骑行85km
求:四天骑行的总路程是多少千米
阅读与理解
第四天 第五天 第六天 第七天
A→B B→C C→D D→E
按照计划,李叔叔后四天还要骑行多少千米?
方法一:直接计算
☆列加法算式计算
1
115+132+118+85
答:李叔叔后四天还要骑450千米。
= 247+118+85
= 365+85
= 450(千米)
按照从左往右的顺序依次计算。
分析与解答
欢欢
2
115+132+118+85
答:李叔叔后四天还要骑450千米。
= 115
= (115+85)+(132+118)
= 200+250
加法交换律
加法结合律
= 450(千米)
+85
+132+118
利用加法交换律和结合律把能凑成整百,整十的数先加起来。
方法二:利用运算律
☆加法交换律和结合律
分析与解答
按照计划,李叔叔后四天还要骑行多少千米?
比较例3的两种方法
115+132+118+85
=85+115+132+118
=(85+115)+(132+118)
=200+250
=450
方法一
115+132+118+85
=247+118+85
=365+85
=450
观察几个连加的加数的特点,想一想:怎样让运算变得简单?
利用加法交换律和结合律把能凑成整十,整百或整千的数结合在一起先加起来,可以使计算简便。
方法二
比一比:哪种方法更简便
想一想,说一说:在刚才运用加法运算律计算过程中,有哪些注意的?
加法简便计算的方法
一看
运算符号
数字特点
二想
凑整 运算定律
三算
准确计算
连加算式仔细算,
运算定律记心间。
整十、整百和整千,
结合先算更简便。
反思与总结
更深入地理解了加法交换律和加法结合律。
先整体观察算式,根据数据特点进行凑整……
解决问题时要有理有据……
通过今天的学习,你有什么收获?
反思与总结
扩展延伸-高斯求和
同学们,你们听说过数学家高斯小时候计算:1+2+3+···+100
的和是多少的故事吗?
(1) 1+2+3+4+…+98+99+100
这几组配对的数的和都为101
100个数共可配100÷2=50(组)
1+2+3+4+···+98+99+100
=101×50
=5050
1+100=101
2+99=101
3+98=101
4+97=101
……
49+52=101
50+51=101
共50个101
* 用合适的方法计算。
教材第23 练习六 第9题
(2)2+4+6+…+16+18+20
这几组配对的数的和都为22
10个数共可配10÷2=5(组)
2+4+6+…+16+18+20
=(2+20) +(4+18) +(6+16)+(8+14) +(10+12)
=22×5
=110
* 用合适的方法计算。
教材第23 练习六 第9题
(3)5+10+15+…+90+95+100
这几组配对的数的和都为105
20个数共可配20÷2=10(组)
5+10+15+…+90+95+100
=105×10
=1050
* 用合适的方法计算。
教材第23 练习六 第9题
(4)20 19+18 17+…+4 3+2 1
1
1
1
1
一共20个数,则有10个1
20 19+18 17+…+4 3+2 1
=(20 19)+(18 17)+…+(4 3) +(2 1)
=1+1+…+1+1
=1×10
=10
* 用合适的方法计算。
解题关键:先观察算式中数据的特点,若算式中数据两两结合可以凑成某个相同的数,可利用分组法将数据两两结合再进行计算。分组时注意一共分成了多少组,有没有数据遗漏。
说一说解决此类问题的关键是什么?
教材第23 练习六 第9题
达标练习,巩固成果
计算下面各题,怎样简便就怎样计算。
425 + 14 + 186 75 + 168 + 25
= 425+(14+186)
= 425+200
= 625
14 + 186
75
+ 25
+ 168
=
= 100+168
= 268
245 + 180 + 20 + 155 67 + 25 + 33 + 75
=
= (245+155)+(180+20)
= 400 +200
= 600
245
+ 155
+ 180 + 20
=
+ 25
+ 75
+ 33
67
= 100 +100
= 200
= (67+33)+(25+75)
教材第20页“做一做”第1题
1
刘老师购买了下列体育用品,一共花了多少钱?
48+55+52+45
=(48+52)+(55+45)
= 100+100
= 200(元)
答:一共花了200元钱。
48元 55元 52元 45元
教材第20页“做一做”第2题
2
225+328+175
=225+175+328
=400+328
=728(元)
答:王阿姨一共收到转账款728元。
3月6日—11日王阿姨共收到转账款多少元?
3
教材第22 练习六 第2题
这堆原木一共多少根?
1根
2根
3根
……
一层一层记下根数
1+2+3+4+5+6+7+8+9+10
= (1+9)+(2+8)+(3+7)+(4+6)+5+10
= 10+10+10+10+5+10
= 10×5+5
= 50+5
= 55(根)
答:这堆原木一共有55根。
原木总数等于每一层原木的根数相加的和。
方法一
4
教材第22 练习六 第4题
这堆原木一共多少根?
1+2+3+4+5+6+7+8+9+10
=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)
=11+11+11+11+11
=11 × 5
=55(根)
答:这堆原木一共有55根。
方法二
4
教材第22 练习六 第4题
2255+355+245
=2255+(355+245)
=2255+600
=2855(元) 答:这台彩电原价2855元。
这台电视机原价多少钱?
彩电原价等于现价加两次降价。
5
教材第23 练习六 第7题
先思考,再计算,怎样简便怎样算。
9 + 99 + 999 + 9999
= (1+1+1+6) +99+999 +9999
= (1+99) + (1+999) + (1+9999)+6
= 100+1000+10000+6
= 11106
比一比,看谁的方法更简便!
9
6
加法运算定律的应用
1. 合理运用加法运算定律可以简便运算。
2. 简算的核心是“凑整”或“相同的数”。
3. 看哪两个数相加能凑成整十、整百或整千,
或相同的数。
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
