第三单元_第06课时_圆锥的体积(教学课件)-六年级数学下册人教版 (1)(共44张PPT)
文档属性
| 名称 | 第三单元_第06课时_圆锥的体积(教学课件)-六年级数学下册人教版 (1)(共44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 16:27:48 | ||
图片预览






文档简介
小学数学·六年级(下)·RJ
第6课时 圆锥的体积
能解决与圆锥体积有关的实际问题,进一步培养动手操作能力。
经历推导圆锥的体积计算公式的过程,体会转化思想。掌握圆锥的体积计算公式。
在公式的推导过程中培养乐于学习、勇于探究的数学情感。在问题解决中体会数学与生活的密切联系。
掌握圆锥体积的计算公式,并能灵活利用公式求圆锥的体积。
理解圆锥体积公式的推导过程及解决生活中的实际问题。
圆柱体积计算公式的推导是把新知转化为旧知,使学生掌握转化的思想,提高推理概括的能力。
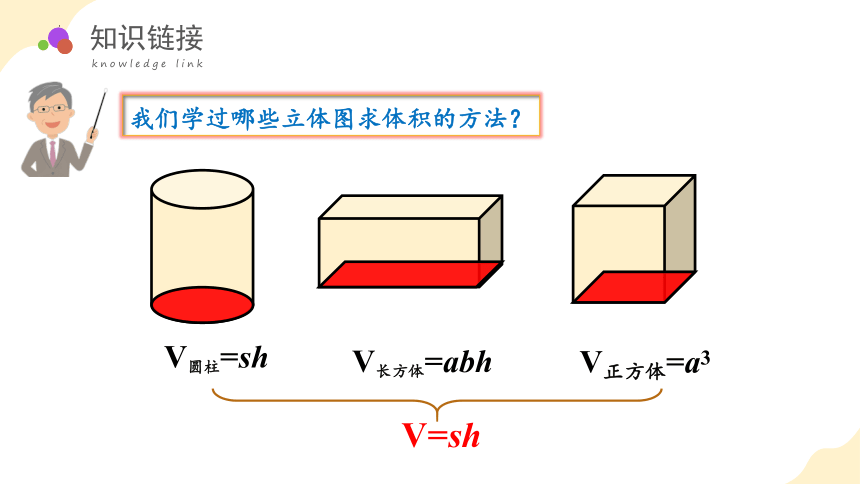
我们学过哪些立体图求体积的方法?
V圆柱=sh
V长方体=abh
V正方体=a3
V=sh
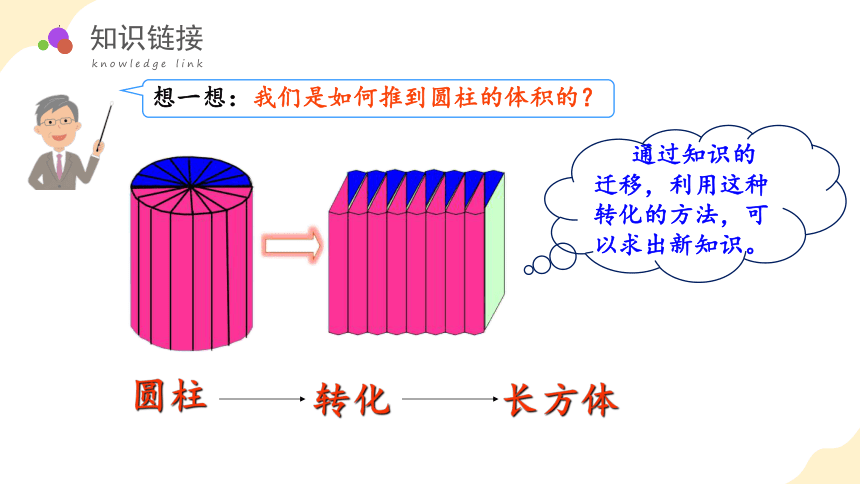
想一想:我们是如何推到圆柱的体积的?
通过知识的迁移,利用这种转化的方法,可以求出新知识。
圆柱
转化
长方体
圆锥体积计算公式的推导
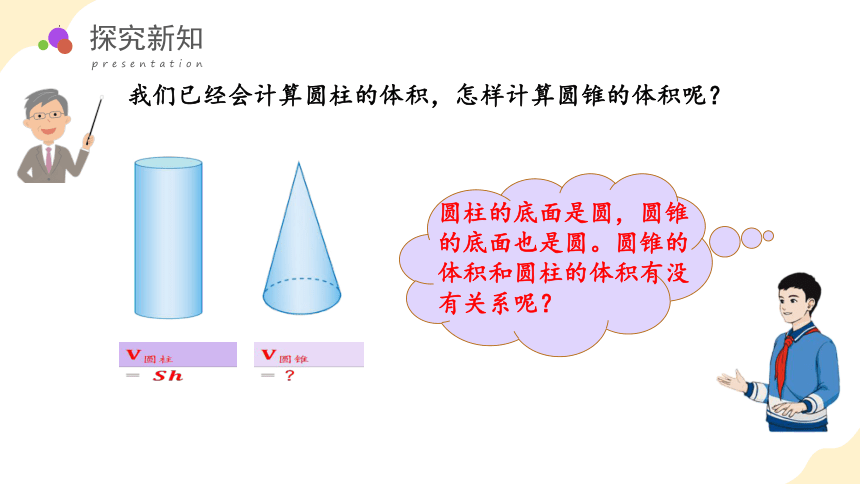
我们已经会计算圆柱的体积,怎样计算圆锥的体积呢?
????圆柱=?????????
?
????圆锥=?
?
圆柱的底面是圆,圆锥的底面也是圆。圆锥的体积和圆柱的体积有没有关系呢?
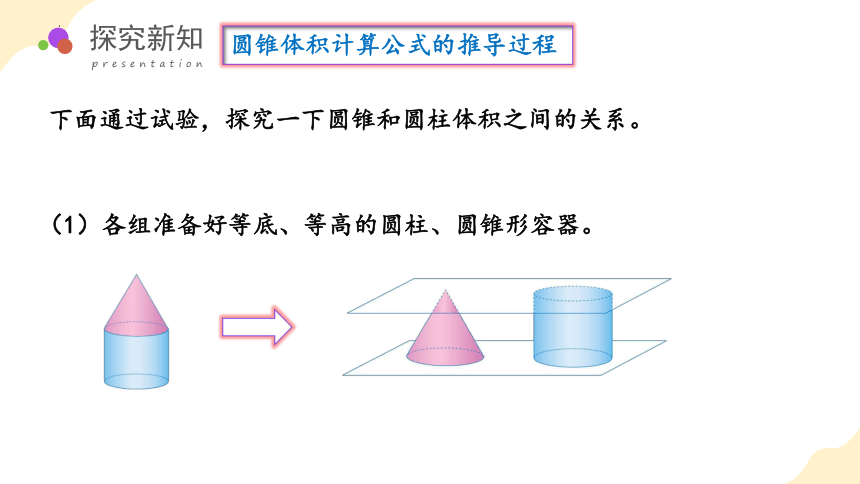
圆锥体积计算公式的推导过程
下面通过试验,探究一下圆锥和圆柱体积之间的关系。
(1)各组准备好等底、等高的圆柱、圆锥形容器。
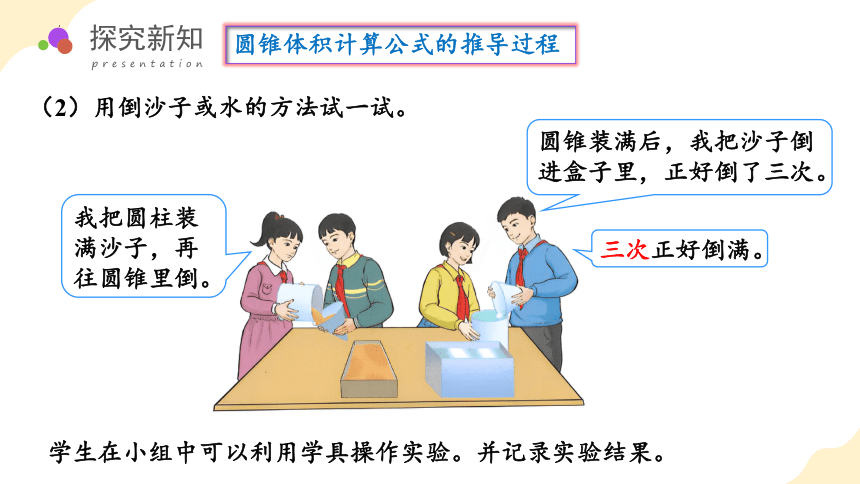
(2)用倒沙子或水的方法试一试。
圆锥装满后,我把沙子倒进盒子里,正好倒了三次。
三次正好倒满。
我把圆柱装满沙子,再往圆锥里倒。
学生在小组中可以利用学具操作实验。并记录实验结果。
圆锥体积计算公式的推导过程
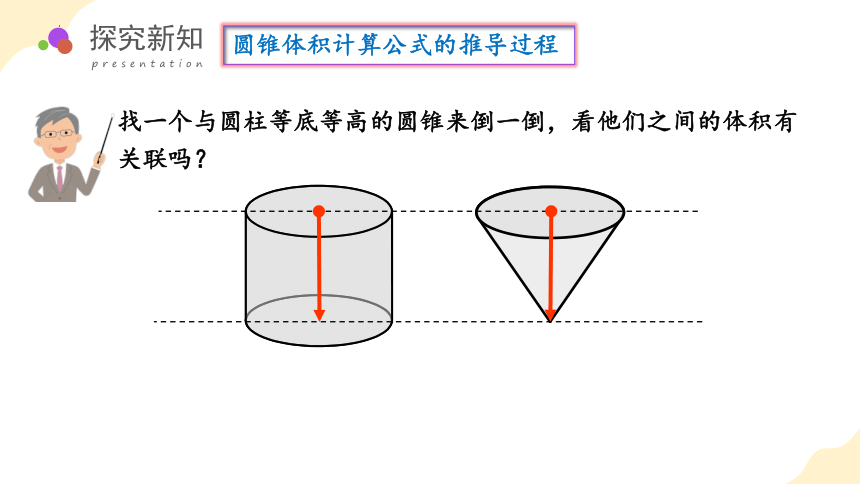
找一个与圆柱等底等高的圆锥来倒一倒,看他们之间的体积有关联吗?
圆锥体积计算公式的推导过程
我们将圆锥容器装满水倒入等底等高的圆柱容器中,第一次。
圆锥体积计算公式的推导过程
倒入第2次
圆锥面积计算公式的推导过程
我们发现倒入3次后,正好倒满。
V 圆柱 = 3V圆锥
=
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
h
h
Ⅴ圆锥 = ????????Ⅴ 圆柱 = ????????sh
?
圆锥的体积= ?????????×
?
圆锥的体积
等于与它等底等高圆柱体积的????????
?
底面积×高
利用圆锥体积公式解决实际问题
工地上有一堆沙子,其形状近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
想一想:要求什么?先求什么?再求什么?
Ⅴ圆锥 = ????????sh
?
工地上有一堆沙子,其形状近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
圆锥的高
圆锥的底面直径
先求:(1)沙堆底面积:
(4÷2)2×3.14=12.56(m2)
工地上有一堆沙子,其形状近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
圆锥的高
圆锥的底面直径
再求:(2)沙堆的体积:
×12.56×1.5 = 6.28(m3)
最后求:(3)沙堆重:
6.28×1.5=9.42(t)
答:这堆沙子大约重9.42吨。
动脑想一想,要求圆锥的体积,必须知道哪些条件?
底面面积和高
V圆锥= Sh
底面半径和高
V圆锥= πr2h
底面直径和高
V圆锥= π h
V圆锥= π h
底面周长和高
圆锥的运用
1.一个圆锥形的零件,底面积是19cm2,高是12cm。这个零件的体积是多少?
V圆锥= Sh
=
×19 ×12=76(cm?)
答:这个零件的体积是76cm? 。
2.如右图,一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高是6cm。每立方厘米钢大约重7.9g。这个铅锤大约重多少克?(得数保留整数。)
想一想:要求什么?先求什么?再求什么?
(2)铅锤的体积:
(1)铅锤的底面积:
25.12×7.9=198.448 ≈198(g)
(3)铅锤的质量:
答:这个铅锤大约重198克 。
×12.56×6=25.12(cm3)
(4÷2)2×3.14=12.56 (cm2)
达标练习,巩固成果
1.(1)一个圆柱的体积是75.36m3,与它等底、等高的圆锥的体积是( )m3。
(2)一个圆锥的体积是141.3m3,与它等底、等高的圆柱的体积是( )m3。
25.12
423.9
75.36÷3=25.12(m3)
141.3×3=423.9(m3)
2.判断下面的说法是否正确,并说一说你的理由。
(1)圆锥的体积等于圆柱体积的 。( )
(2)圆柱的体积大于与它等底、等高的圆锥的体积。( )
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。( )
×
√
×
3.一个圆锥的底面周长是31.4cm,高是9cm。它的体积是多少?
= ×3.14×(31.4÷3.14÷2)2×9
= 235.5(cm3)
V = π ( )2 h
2π
C
答:它的体积是235.5cm3。
4.一堆煤呈圆锥形,高为2m,底面周长为18.84m。这堆煤的体积是多少?已知每立方米的煤大约重1.4t,这堆煤大约重多少吨?(得数保留整数。)
×3.14×(18.84÷3.14÷2)2×2=18.84(m3)
答:这堆煤的体积是18.84m3。这堆煤大约重 26 吨。
18.84×1.4≈26(吨)
5. 一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
4×3=12(dm)
答:圆锥的高是12dm 。
想一想,当一个圆柱与一个圆锥的底面积和体积分别相等时,圆锥的高与圆柱的高又是什么关系呢?
6.一个圆柱与圆锥的体积和高分别相等,已知圆锥的底面积是28.26平方米,圆柱的底面积是多少?
在等高等体积的前提下,圆柱底面积是圆锥底面积的三分之一,
故而 28.26?× ? ? =9.42(平方米)
7.用底面半径和高分别是6cm、12cm的空心圆锥和空心圆柱各一个,组成竖放的容器(如右图)。在这个容器内注入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高2cm。若将这个容器上面封住并倒立,细沙的高度是多少厘米?
×12+2=6(cm)
答:细沙的高度是6厘米。
www.youyi100.com
200平方千米=200000000平方米
50mm=0.05m
0.05×200000000=10000000(立方米)=1000(万立方米)
1000×25%=250(万立方米)
250>200
答:该日该地区总降水为1000万立方米,这些雨水的25%能满足绿化用水。
8.一定时间内,降落在水平面上的水,在未经蒸发、渗漏、流失情况下所积的深度,称为降水量(通常以毫米为单位)。某地区的土地面积为200km?,某日平均降水量为50mm,该日该地区总降水为多少万立方米?该地区一年绿化用水为200万立方米,这些雨水的25%能满足绿化所需吗?
9.小雨的水壶有一个布套(如右图)。
(1)做这个布套至少用了多少布料?
3.14×10×20+3.14×(10÷2)2×2=785(cm2)
答:至少用了785平方厘米的布料。
3.14×(10÷2)2×20=1570(cm3)=1.57(L) 1.57 >1
答:一壶水够1.5L 。
(2)一壶水够1.5L吗?(水壶和布套的厚度忽略不计。)
10.一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是 4dm,圆柱高2dm,圆锥高4.2dm。每立方分米稻谷大约重0.65kg。(1)这个漏斗最多能装多少千克稻谷?(稻谷不超出漏斗上沿,得数保留整数。)
28×70%=19.6(kg)
答:一漏斗稻谷能磨19.6千克大米。
[3.14×(4÷2)2×2+ ×3.14×(4÷2)2×4.2 ]×0.65≈28(kg)
答:这个漏斗最多能装28千克稻谷。
(2)如果稻谷的出米率是70%,一漏斗稻谷能磨多少大米?
11. 把一块长方体钢坯熔铸成一根底面直径为4dm的圆柱形钢材,求钢材的长度。
12.56×5×4 =251.28(dm3)
3.14×(4÷2)2=12.56(dm2)
251.28÷12.56 =20(dm)
答:钢材的长度是20 dm。
12.一个圆锥形沙堆,底面积是28.6m2,高是3m。用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
×28.6×3=28.6 (m3)
2cm=0.02m
28.6÷10÷0.02=143(m)
答:能铺 143 米。
形变,体不变
等积变形问题的解决方法
13.一个圆柱形金属零件上有9个圆柱形孔(如右图)。这个零件的金属用量大约是多少立方分米? (得数保留两位小数。)
大圆柱的底面积:3.14×(12÷2)2=113.04(cm2)
圆柱孔的底面积之和:
3.14×(4÷2)2+3.14×(2÷2)2 ×8=37.68(cm2)
零件的体积:(113.04-37.68)×10=753.6(cm3)≈0.75(dm3 )
答:这个零件的金属用量大约是0.75立方分米。
14. 有块正方体的木料,它的棱长是4dm。把这块木料加工成一个圆柱。这个圆柱的体积最大是多少?
在正方体中截取一个最大的圆柱,圆柱的体积是正方体的体积78.5%
4×4×4×78.5%=50.24(dm3)
答:这个圆柱的体积是50.24dm3。
14. 有块正方体的木料,它的棱长是4dm。把这块木料加工成一个圆柱。这个圆柱的体积最大是多少?
在正方体中截取一个最大的圆柱,圆柱的体积是正方体的体积78.5%
答:该桶最多能装62.8L水。
3.14×(4÷2)2×5=62.8(dm3)=62.8(L)
联系生活
15.一个圆柱形木桶,底面内直径为4dm,桶口距底面最小高度为5dm,最大高度为7dm。这个木桶如右图放置时,最多能装多少升水?
同学们,这节课你有哪些收获?
圆锥的体积= ?????????×
?
圆锥的体积
等于与它等底等高圆柱体积的????????
?
底面积×高
h
h
Ⅴ圆锥 = ????????Ⅴ 圆柱 = ????????sh
?
Ⅴ圆锥 = ????????sh
?
★ 完成《分层作业》;
★★ 通过实验进一步的探究圆锥和圆锥体积之间的关系,准备等底不等高,或者等高不等底之间的体积关系。
第6课时 圆锥的体积
能解决与圆锥体积有关的实际问题,进一步培养动手操作能力。
经历推导圆锥的体积计算公式的过程,体会转化思想。掌握圆锥的体积计算公式。
在公式的推导过程中培养乐于学习、勇于探究的数学情感。在问题解决中体会数学与生活的密切联系。
掌握圆锥体积的计算公式,并能灵活利用公式求圆锥的体积。
理解圆锥体积公式的推导过程及解决生活中的实际问题。
圆柱体积计算公式的推导是把新知转化为旧知,使学生掌握转化的思想,提高推理概括的能力。
我们学过哪些立体图求体积的方法?
V圆柱=sh
V长方体=abh
V正方体=a3
V=sh
想一想:我们是如何推到圆柱的体积的?
通过知识的迁移,利用这种转化的方法,可以求出新知识。
圆柱
转化
长方体
圆锥体积计算公式的推导
我们已经会计算圆柱的体积,怎样计算圆锥的体积呢?
????圆柱=?????????
?
????圆锥=?
?
圆柱的底面是圆,圆锥的底面也是圆。圆锥的体积和圆柱的体积有没有关系呢?
圆锥体积计算公式的推导过程
下面通过试验,探究一下圆锥和圆柱体积之间的关系。
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
圆锥装满后,我把沙子倒进盒子里,正好倒了三次。
三次正好倒满。
我把圆柱装满沙子,再往圆锥里倒。
学生在小组中可以利用学具操作实验。并记录实验结果。
圆锥体积计算公式的推导过程
找一个与圆柱等底等高的圆锥来倒一倒,看他们之间的体积有关联吗?
圆锥体积计算公式的推导过程
我们将圆锥容器装满水倒入等底等高的圆柱容器中,第一次。
圆锥体积计算公式的推导过程
倒入第2次
圆锥面积计算公式的推导过程
我们发现倒入3次后,正好倒满。
V 圆柱 = 3V圆锥
=
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
h
h
Ⅴ圆锥 = ????????Ⅴ 圆柱 = ????????sh
?
圆锥的体积= ?????????×
?
圆锥的体积
等于与它等底等高圆柱体积的????????
?
底面积×高
利用圆锥体积公式解决实际问题
工地上有一堆沙子,其形状近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
想一想:要求什么?先求什么?再求什么?
Ⅴ圆锥 = ????????sh
?
工地上有一堆沙子,其形状近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
圆锥的高
圆锥的底面直径
先求:(1)沙堆底面积:
(4÷2)2×3.14=12.56(m2)
工地上有一堆沙子,其形状近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
圆锥的高
圆锥的底面直径
再求:(2)沙堆的体积:
×12.56×1.5 = 6.28(m3)
最后求:(3)沙堆重:
6.28×1.5=9.42(t)
答:这堆沙子大约重9.42吨。
动脑想一想,要求圆锥的体积,必须知道哪些条件?
底面面积和高
V圆锥= Sh
底面半径和高
V圆锥= πr2h
底面直径和高
V圆锥= π h
V圆锥= π h
底面周长和高
圆锥的运用
1.一个圆锥形的零件,底面积是19cm2,高是12cm。这个零件的体积是多少?
V圆锥= Sh
=
×19 ×12=76(cm?)
答:这个零件的体积是76cm? 。
2.如右图,一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高是6cm。每立方厘米钢大约重7.9g。这个铅锤大约重多少克?(得数保留整数。)
想一想:要求什么?先求什么?再求什么?
(2)铅锤的体积:
(1)铅锤的底面积:
25.12×7.9=198.448 ≈198(g)
(3)铅锤的质量:
答:这个铅锤大约重198克 。
×12.56×6=25.12(cm3)
(4÷2)2×3.14=12.56 (cm2)
达标练习,巩固成果
1.(1)一个圆柱的体积是75.36m3,与它等底、等高的圆锥的体积是( )m3。
(2)一个圆锥的体积是141.3m3,与它等底、等高的圆柱的体积是( )m3。
25.12
423.9
75.36÷3=25.12(m3)
141.3×3=423.9(m3)
2.判断下面的说法是否正确,并说一说你的理由。
(1)圆锥的体积等于圆柱体积的 。( )
(2)圆柱的体积大于与它等底、等高的圆锥的体积。( )
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。( )
×
√
×
3.一个圆锥的底面周长是31.4cm,高是9cm。它的体积是多少?
= ×3.14×(31.4÷3.14÷2)2×9
= 235.5(cm3)
V = π ( )2 h
2π
C
答:它的体积是235.5cm3。
4.一堆煤呈圆锥形,高为2m,底面周长为18.84m。这堆煤的体积是多少?已知每立方米的煤大约重1.4t,这堆煤大约重多少吨?(得数保留整数。)
×3.14×(18.84÷3.14÷2)2×2=18.84(m3)
答:这堆煤的体积是18.84m3。这堆煤大约重 26 吨。
18.84×1.4≈26(吨)
5. 一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
4×3=12(dm)
答:圆锥的高是12dm 。
想一想,当一个圆柱与一个圆锥的底面积和体积分别相等时,圆锥的高与圆柱的高又是什么关系呢?
6.一个圆柱与圆锥的体积和高分别相等,已知圆锥的底面积是28.26平方米,圆柱的底面积是多少?
在等高等体积的前提下,圆柱底面积是圆锥底面积的三分之一,
故而 28.26?× ? ? =9.42(平方米)
7.用底面半径和高分别是6cm、12cm的空心圆锥和空心圆柱各一个,组成竖放的容器(如右图)。在这个容器内注入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高2cm。若将这个容器上面封住并倒立,细沙的高度是多少厘米?
×12+2=6(cm)
答:细沙的高度是6厘米。
www.youyi100.com
200平方千米=200000000平方米
50mm=0.05m
0.05×200000000=10000000(立方米)=1000(万立方米)
1000×25%=250(万立方米)
250>200
答:该日该地区总降水为1000万立方米,这些雨水的25%能满足绿化用水。
8.一定时间内,降落在水平面上的水,在未经蒸发、渗漏、流失情况下所积的深度,称为降水量(通常以毫米为单位)。某地区的土地面积为200km?,某日平均降水量为50mm,该日该地区总降水为多少万立方米?该地区一年绿化用水为200万立方米,这些雨水的25%能满足绿化所需吗?
9.小雨的水壶有一个布套(如右图)。
(1)做这个布套至少用了多少布料?
3.14×10×20+3.14×(10÷2)2×2=785(cm2)
答:至少用了785平方厘米的布料。
3.14×(10÷2)2×20=1570(cm3)=1.57(L) 1.57 >1
答:一壶水够1.5L 。
(2)一壶水够1.5L吗?(水壶和布套的厚度忽略不计。)
10.一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是 4dm,圆柱高2dm,圆锥高4.2dm。每立方分米稻谷大约重0.65kg。(1)这个漏斗最多能装多少千克稻谷?(稻谷不超出漏斗上沿,得数保留整数。)
28×70%=19.6(kg)
答:一漏斗稻谷能磨19.6千克大米。
[3.14×(4÷2)2×2+ ×3.14×(4÷2)2×4.2 ]×0.65≈28(kg)
答:这个漏斗最多能装28千克稻谷。
(2)如果稻谷的出米率是70%,一漏斗稻谷能磨多少大米?
11. 把一块长方体钢坯熔铸成一根底面直径为4dm的圆柱形钢材,求钢材的长度。
12.56×5×4 =251.28(dm3)
3.14×(4÷2)2=12.56(dm2)
251.28÷12.56 =20(dm)
答:钢材的长度是20 dm。
12.一个圆锥形沙堆,底面积是28.6m2,高是3m。用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
×28.6×3=28.6 (m3)
2cm=0.02m
28.6÷10÷0.02=143(m)
答:能铺 143 米。
形变,体不变
等积变形问题的解决方法
13.一个圆柱形金属零件上有9个圆柱形孔(如右图)。这个零件的金属用量大约是多少立方分米? (得数保留两位小数。)
大圆柱的底面积:3.14×(12÷2)2=113.04(cm2)
圆柱孔的底面积之和:
3.14×(4÷2)2+3.14×(2÷2)2 ×8=37.68(cm2)
零件的体积:(113.04-37.68)×10=753.6(cm3)≈0.75(dm3 )
答:这个零件的金属用量大约是0.75立方分米。
14. 有块正方体的木料,它的棱长是4dm。把这块木料加工成一个圆柱。这个圆柱的体积最大是多少?
在正方体中截取一个最大的圆柱,圆柱的体积是正方体的体积78.5%
4×4×4×78.5%=50.24(dm3)
答:这个圆柱的体积是50.24dm3。
14. 有块正方体的木料,它的棱长是4dm。把这块木料加工成一个圆柱。这个圆柱的体积最大是多少?
在正方体中截取一个最大的圆柱,圆柱的体积是正方体的体积78.5%
答:该桶最多能装62.8L水。
3.14×(4÷2)2×5=62.8(dm3)=62.8(L)
联系生活
15.一个圆柱形木桶,底面内直径为4dm,桶口距底面最小高度为5dm,最大高度为7dm。这个木桶如右图放置时,最多能装多少升水?
同学们,这节课你有哪些收获?
圆锥的体积= ?????????×
?
圆锥的体积
等于与它等底等高圆柱体积的????????
?
底面积×高
h
h
Ⅴ圆锥 = ????????Ⅴ 圆柱 = ????????sh
?
Ⅴ圆锥 = ????????sh
?
★ 完成《分层作业》;
★★ 通过实验进一步的探究圆锥和圆锥体积之间的关系,准备等底不等高,或者等高不等底之间的体积关系。
