第三单元_第06课时_长方体和正方体的体积(教学课件)-五年级数学下册人教版 (2)(共39张PPT)
文档属性
| 名称 | 第三单元_第06课时_长方体和正方体的体积(教学课件)-五年级数学下册人教版 (2)(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 16:29:54 | ||
图片预览








文档简介
(共39张PPT)
小学数学·五年级(下)·RJ
第7课时 体积单位间的进率
会正确应用体积单位间的进率进行名数的变换,并解决一些简单的实际问题。
经历探究体积单位间的进率的过程,掌握相邻两个体积单位间的进率。
培养学生的学习迁移能力和探究能力,使学生会应用猜想、验证等方法解决数学问题。
掌握体积单位间的进率,理解体积单位间的换算方法。
会正确应用体积单位间的进率进行名数的变换,并解决一些简单的实际问题。
培养学生类比、推理能力,感受数学知识间的相互联系。
(1)常用的长度单位有哪些?相邻的两个单位间的进率是多少?
相邻长度单位间进率是:10
常用的长度单位:米、分米、厘米
相邻单位的进率:1米=10分米
1分米=10厘米
1厘米=10毫米
(2)常用的面积单位有哪些?相邻的两个单位间的进率是多少?
相邻面积单位间进率是:100
常用的面积单位:平方米、平方分米、平方厘米
相邻单位的进率: 1平方米=100平方分米
1平方分米=100平方厘米
口答填空,并说明算法。
4米=( )分米=( )厘米
80000平方厘米=( )平方分米=( )平方米
高级单位变为低级单位:数字会变大
高级单位的数×进率
低级单位变为高级单位:数字会变小
低级单位的数÷进率
40
400
800
8
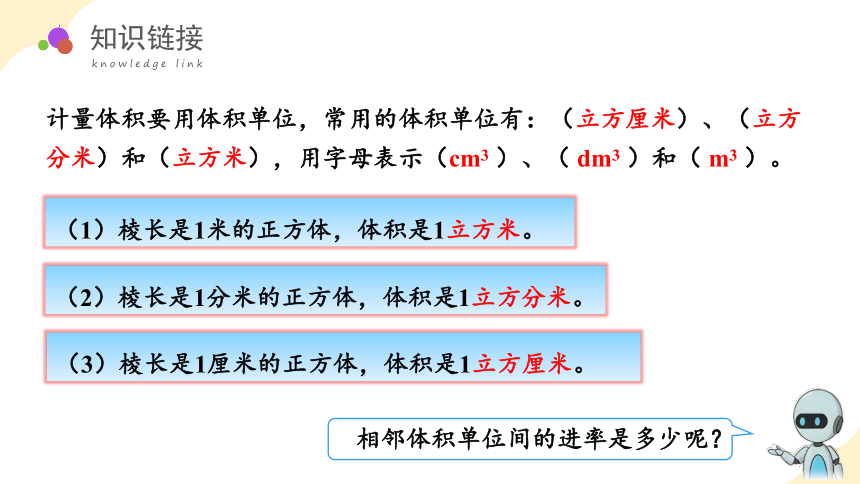
相邻体积单位间的进率是多少呢?
计量体积要用体积单位,常用的体积单位有:(立方厘米)、(立方分米)和(立方米),用字母表示(cm3 )、( dm3 )和( m3 )。
(3)棱长是1厘米的正方体,体积是1立方厘米。
(2)棱长是1分米的正方体,体积是1立方分米。
(1)棱长是1米的正方体,体积是1立方米。
探究体积单位间的进率
探究体积单位间的进率
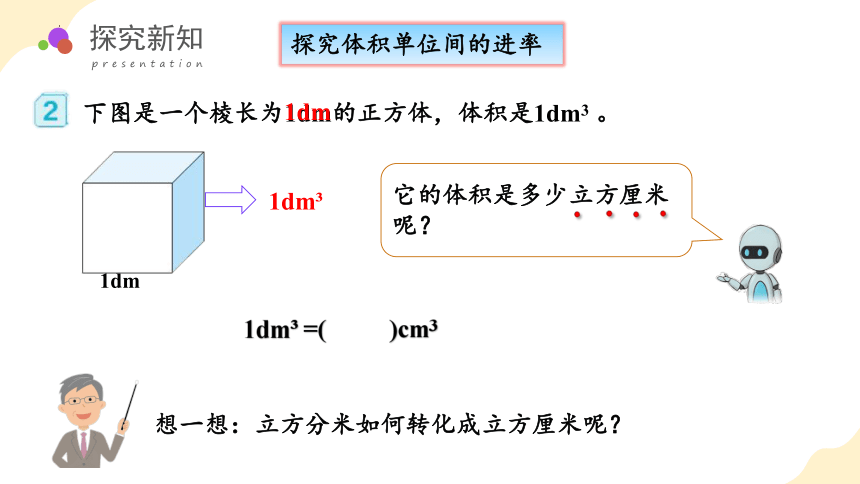
下图是一个棱长为1dm的正方体,体积是1dm3 。
想一想:立方分米如何转化成立方厘米呢?
1dm
1dm =( )cm3
1dm
1dm
它的体积是多少立方厘米呢?
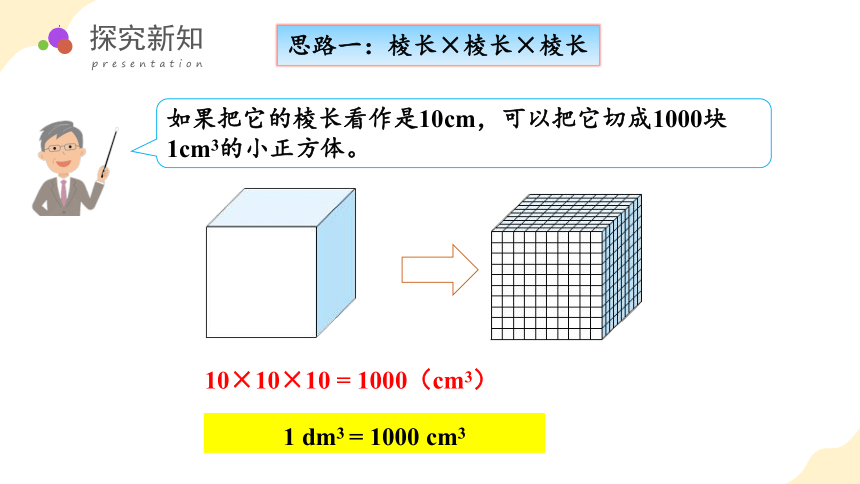
如果把它的棱长看作是10cm,可以把它切成1000块1cm3的小正方体。
10×10×10 = 1000(cm3)
1 dm3 = 1000 cm3
思路一:棱长×棱长×棱长
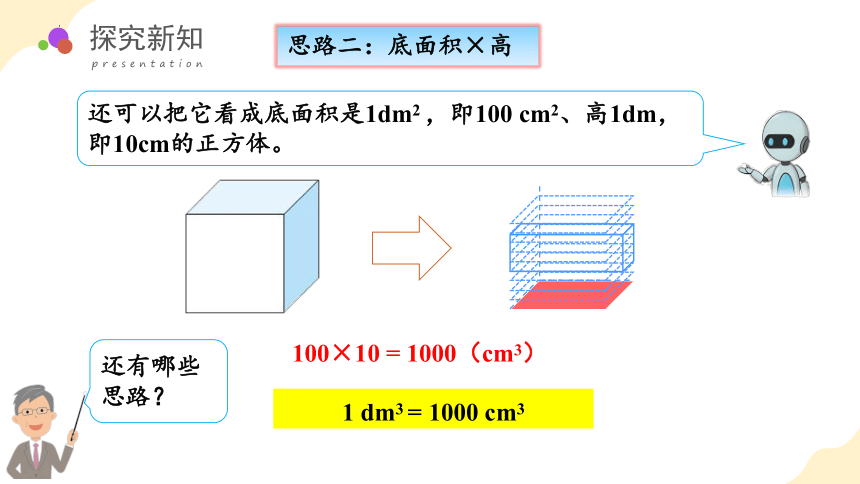
还可以把它看成底面积是1dm2 ,即100 cm2、高1dm,即10cm的正方体。
100×10 = 1000(cm3)
1 dm3 = 1000 cm3
思路二:底面积×高
还有哪些思路?
输入标题
1 立方米=( )立方分米
尝试用上面的方法推算立方米和立方分米之间关系。
可以把正方体的棱长1 m看作是10 dm,每条棱都能分成相等的10份,共能分成1000个1 dm3的小正方体……
把棱长看成10 dm,底面积就是100 ,所以体积等于100×10=1000 dm3……
根据正方体的体积=棱长×棱长×棱长……
类比探究
一级标题
输入标题
1立方米=( )立方厘米
1000000
1立方米=( )立方分米
1000
1立方分米=( )立方厘米
1000
1000
相邻两个体积单位间的进率是1000。
总结与拓展
体积单位之间的换算与应用
想:
1m = dm
3.8m = dm
1m =1000dm
3.8×1000=3800dm
1000
3800
高级单位
乘进率,小数点向右移
低级单位
(1)3.8m 是多少立方分米?
3.8×1000
(2)2400cm 是多少立方分米?
想:
cm =1dm
2400cm = dm
1dm =1000cm
2400÷1000=2.4dm
低级单位
除以进率,小数点向左移
高级单位
1000
2.4
2400÷1000
这个牛奶包装箱的体积是多少
50cm=5dm
40cm=4dm
30cm=3dm
V=a b h
=5×3×4
=60(dm3)
方法一:
箱上的尺寸一般是这个长方体的长、宽、高。
答:这个牛奶包装箱的体积是60dm3 。
这个牛奶包装箱的体积是多少
方法二:
箱上的尺寸一般是这个长方体的长、宽、高。
60000cm3=60dm3
V=a b h
=50×30×40
=60000(cm3)
答:这个牛奶包装箱的体积是60dm3 。
3.5dm = cm
700dm = m
0.25m = cm
3.5×1000=3500cm
3500
700÷1000=0.7m
0.25×1000=250dm
0.7
250×1000=250000cm
250000
1. 想一想,填一填。
2.要砌一道长15m、厚24cm、高3m的砖墙。如果每立方米用砖525块,一共要用砖多少块?
24 cm=0.24 m
V =a b h
=15×0.24×3
=10.8(m3)
10.8×525=5670(块)
答:一共要用砖5670块。
达标练习,巩固成果
1.02m =______ dm
960dm =______ m
6270cm2=______ dm2
36000cm =______m
8.63m2=______dm2
23dm =______cm
1020
0.96
62.7
0.036
863
23000
1.
11.76 dm = 11760 cm
25×16×18 = 7200(cm )
7200 cm3<11760 cm3
所以装得进去。
2. 一个长方体包装盒,从里面量长 28 cm,宽20 cm,里面的体积为11.76 dm3。用它包装一个长 25 cm,宽 16 cm、高 18 cm的玻璃器皿,是否装得进去?说一说你的理由。
3.某小区新安装了50个混凝土凳子(如右图所示)。凳面的长、宽、高分别是100cm、45cm、4.5cm,凳腿的长、宽、高分别是45cm、5cm、35cm。做这些凳子至少用了多少方混凝土?
凳面的体积:100×45×4.5×50=1012500(cm3)
凳腿的体积:45×5×35×2×50=787500(cm3)
总体积:1012500+787500=1800000(cm3)
答:做这些凳子至少用了 1.8 方混凝土。
1800000 cm3 =1.8 m3 =1.8 方
4.“六一”儿童节前,小学生用棱长 3 cm的正方体塑料拼插积木在广场中央搭起了一面长 6 m、高 2.7 m、厚 6 cm 的心愿墙。这面墙一共用了多少块积木?
600×270×6=972000(㎝3)
3×3×3=27(㎝3)
972000÷27=36000(块)
答:这面墙一共用了36000块积木。
6m=600㎝ 2.7m=270㎝
5.一个长方体的无盖玻璃水族箱,长是 6 m,宽是 60 cm,高是 1.5 m。制作这个水族箱需要用多少平方米的玻璃?它的体积是多少?
60cm=0.6m
占地面积:6×0.6=3.6(m2)
玻璃的表面积:3.6+6×1.5×2+0.6×1.5×2=23.4(m2)
体积:3.6×1.5=5.4(m3)
答:这个水族箱需要用23.4m2的玻璃,它的体积是5.4m3。
6.将 7.6 m3 的沙子铺在一个长 5 m、宽 38 dm 的沙坑里,可以铺多厚?
38 dm=3.8 m
7.6÷(5×3.8)=0.4(m)
答:可以铺0.4m厚。
7.圈出每组中与其他数据不相等的那个数据。
(1)5.08 m 50800 cm 5080 dm 5080000 cm
(2)6039 dm2 6.039 m2 603900 cm2 60.39 m2
(3)1500 cm 1500 dm 15 m 150 dm
8.修建长城所用的某块砖的尺寸如右图所示。这块长城砖的体积是多少?
40×10×20=8000(cm3)
答:这块长城砖体积是8000cm3。
9.一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是 6 cm、4 cm、5 cm,正方体的棱长是多少厘米?它们的体积相等吗?
6cm
4cm
5cm
?cm
正方体的棱长:(6+5+4)×4÷12=5(cm)
正方体的体积:5×5×5=125(cm3)
长方体的体积:6×5×4=120(cm3)
答:正方体的棱长是5cm,长方体和正方体的体积不相等,正方体的体积大。
10*茶厂工人要将长、宽均为 20 cm,高为 10 cm 的长方体茶盒装入棱长为 30 cm(从里面量)的正方体纸箱,一箱最多能装几盒?怎样才能装下?
20cm
20cm
10cm
求能装几盒,可以用纸箱体积除以茶盒体积吗?
10cm=1dm
3×3×3=27(dm3)
20cm=2dm
30cm=3dm
2×2×1=4 (dm3)
27÷4=6.75(盒)
答:一箱最多能装6盒。
30cm
30cm
30cm
怎样装呢?纸箱棱长30cm,放一个茶盒后就剩10cm……
30cm
正方体纸箱的棱长不是长方体茶盒的长和宽的整数倍,要达到最大盒数,就要合理分配空间。放一个茶盒后就剩10cm,旁边只能再竖着放,这样才可以装下6盒。
10*茶厂工人要将长、宽均为 20 cm,高为 10 cm 的长方体茶盒装入棱长为 30 cm(从里面量)的正方体纸箱,一箱最多能装几盒?怎样才能装下?
11. 一根长方体木料长1.2m、宽6dm、高5dm,现在要将它锯成棱长是2dm的正方体小块,最多可以锯多少个?
1.2m=12dm
12÷2=6(个)
6÷2=3(行)
5÷2=2(层)……1(dm)
6×3×2=36(个)
答:最多可以锯36个。
12.把棱长为1m的正方体木块切割成棱长是1cm的小正方体,这些小正方体一个挨一个地连起来,可以排多长?
1×1×1=1(m )=1000000cm
1×1×1=1(cm )
1000000÷1=1000000(个)
1×1000000=1000000(cm)=10km
答:可以排10km。
13.前进小学修一个长80m、宽50m的长方形操场,先铺15cm厚的三合土,再铺8cm厚的煤渣,需要三合土和煤渣各多少立方米?
答:需要三合土600m ,煤渣320m 。
15cm=0.15m
三合土:80×50×0.15=600(m )
煤渣:80×50×0.08=320(m )
8cm=0.08m
你知道吗?
人们很早就得出长方体、圆柱等形体的体积计算公式。因为它们是河堤、谷仓等的常见形状,而且还有计算体积的需要。
我国古代数学名著《九章算术》中,集中而正确地给出了立体图形的体积计算公式。书中在求底面是正方形的长方体体积时,是这样说的:“方自乘,以高乘之即积尺。”就是说先用边长乘边长得底面积,再乘高就得到长方体的体积。
同学们,这节课你有哪些收获?
单位进率
1.相邻体积单位之间的进率是1000。
1dm =1000cm 1m =1000dm
2.高级单位转换成为低级单位,要乘进率,小数点向右移;低级单位转化成高级单位,要除以进率,小数点向左移。
★ 完成《分层作业》
★★ 在解决有关体积的实际问题时,要看清已知条件的单位是否统一,如果不统一,要先统一单位,再进行计算。动手制作学过单位的进率表。
小学数学·五年级(下)·RJ
第7课时 体积单位间的进率
会正确应用体积单位间的进率进行名数的变换,并解决一些简单的实际问题。
经历探究体积单位间的进率的过程,掌握相邻两个体积单位间的进率。
培养学生的学习迁移能力和探究能力,使学生会应用猜想、验证等方法解决数学问题。
掌握体积单位间的进率,理解体积单位间的换算方法。
会正确应用体积单位间的进率进行名数的变换,并解决一些简单的实际问题。
培养学生类比、推理能力,感受数学知识间的相互联系。
(1)常用的长度单位有哪些?相邻的两个单位间的进率是多少?
相邻长度单位间进率是:10
常用的长度单位:米、分米、厘米
相邻单位的进率:1米=10分米
1分米=10厘米
1厘米=10毫米
(2)常用的面积单位有哪些?相邻的两个单位间的进率是多少?
相邻面积单位间进率是:100
常用的面积单位:平方米、平方分米、平方厘米
相邻单位的进率: 1平方米=100平方分米
1平方分米=100平方厘米
口答填空,并说明算法。
4米=( )分米=( )厘米
80000平方厘米=( )平方分米=( )平方米
高级单位变为低级单位:数字会变大
高级单位的数×进率
低级单位变为高级单位:数字会变小
低级单位的数÷进率
40
400
800
8
相邻体积单位间的进率是多少呢?
计量体积要用体积单位,常用的体积单位有:(立方厘米)、(立方分米)和(立方米),用字母表示(cm3 )、( dm3 )和( m3 )。
(3)棱长是1厘米的正方体,体积是1立方厘米。
(2)棱长是1分米的正方体,体积是1立方分米。
(1)棱长是1米的正方体,体积是1立方米。
探究体积单位间的进率
探究体积单位间的进率
下图是一个棱长为1dm的正方体,体积是1dm3 。
想一想:立方分米如何转化成立方厘米呢?
1dm
1dm =( )cm3
1dm
1dm
它的体积是多少立方厘米呢?
如果把它的棱长看作是10cm,可以把它切成1000块1cm3的小正方体。
10×10×10 = 1000(cm3)
1 dm3 = 1000 cm3
思路一:棱长×棱长×棱长
还可以把它看成底面积是1dm2 ,即100 cm2、高1dm,即10cm的正方体。
100×10 = 1000(cm3)
1 dm3 = 1000 cm3
思路二:底面积×高
还有哪些思路?
输入标题
1 立方米=( )立方分米
尝试用上面的方法推算立方米和立方分米之间关系。
可以把正方体的棱长1 m看作是10 dm,每条棱都能分成相等的10份,共能分成1000个1 dm3的小正方体……
把棱长看成10 dm,底面积就是100 ,所以体积等于100×10=1000 dm3……
根据正方体的体积=棱长×棱长×棱长……
类比探究
一级标题
输入标题
1立方米=( )立方厘米
1000000
1立方米=( )立方分米
1000
1立方分米=( )立方厘米
1000
1000
相邻两个体积单位间的进率是1000。
总结与拓展
体积单位之间的换算与应用
想:
1m = dm
3.8m = dm
1m =1000dm
3.8×1000=3800dm
1000
3800
高级单位
乘进率,小数点向右移
低级单位
(1)3.8m 是多少立方分米?
3.8×1000
(2)2400cm 是多少立方分米?
想:
cm =1dm
2400cm = dm
1dm =1000cm
2400÷1000=2.4dm
低级单位
除以进率,小数点向左移
高级单位
1000
2.4
2400÷1000
这个牛奶包装箱的体积是多少
50cm=5dm
40cm=4dm
30cm=3dm
V=a b h
=5×3×4
=60(dm3)
方法一:
箱上的尺寸一般是这个长方体的长、宽、高。
答:这个牛奶包装箱的体积是60dm3 。
这个牛奶包装箱的体积是多少
方法二:
箱上的尺寸一般是这个长方体的长、宽、高。
60000cm3=60dm3
V=a b h
=50×30×40
=60000(cm3)
答:这个牛奶包装箱的体积是60dm3 。
3.5dm = cm
700dm = m
0.25m = cm
3.5×1000=3500cm
3500
700÷1000=0.7m
0.25×1000=250dm
0.7
250×1000=250000cm
250000
1. 想一想,填一填。
2.要砌一道长15m、厚24cm、高3m的砖墙。如果每立方米用砖525块,一共要用砖多少块?
24 cm=0.24 m
V =a b h
=15×0.24×3
=10.8(m3)
10.8×525=5670(块)
答:一共要用砖5670块。
达标练习,巩固成果
1.02m =______ dm
960dm =______ m
6270cm2=______ dm2
36000cm =______m
8.63m2=______dm2
23dm =______cm
1020
0.96
62.7
0.036
863
23000
1.
11.76 dm = 11760 cm
25×16×18 = 7200(cm )
7200 cm3<11760 cm3
所以装得进去。
2. 一个长方体包装盒,从里面量长 28 cm,宽20 cm,里面的体积为11.76 dm3。用它包装一个长 25 cm,宽 16 cm、高 18 cm的玻璃器皿,是否装得进去?说一说你的理由。
3.某小区新安装了50个混凝土凳子(如右图所示)。凳面的长、宽、高分别是100cm、45cm、4.5cm,凳腿的长、宽、高分别是45cm、5cm、35cm。做这些凳子至少用了多少方混凝土?
凳面的体积:100×45×4.5×50=1012500(cm3)
凳腿的体积:45×5×35×2×50=787500(cm3)
总体积:1012500+787500=1800000(cm3)
答:做这些凳子至少用了 1.8 方混凝土。
1800000 cm3 =1.8 m3 =1.8 方
4.“六一”儿童节前,小学生用棱长 3 cm的正方体塑料拼插积木在广场中央搭起了一面长 6 m、高 2.7 m、厚 6 cm 的心愿墙。这面墙一共用了多少块积木?
600×270×6=972000(㎝3)
3×3×3=27(㎝3)
972000÷27=36000(块)
答:这面墙一共用了36000块积木。
6m=600㎝ 2.7m=270㎝
5.一个长方体的无盖玻璃水族箱,长是 6 m,宽是 60 cm,高是 1.5 m。制作这个水族箱需要用多少平方米的玻璃?它的体积是多少?
60cm=0.6m
占地面积:6×0.6=3.6(m2)
玻璃的表面积:3.6+6×1.5×2+0.6×1.5×2=23.4(m2)
体积:3.6×1.5=5.4(m3)
答:这个水族箱需要用23.4m2的玻璃,它的体积是5.4m3。
6.将 7.6 m3 的沙子铺在一个长 5 m、宽 38 dm 的沙坑里,可以铺多厚?
38 dm=3.8 m
7.6÷(5×3.8)=0.4(m)
答:可以铺0.4m厚。
7.圈出每组中与其他数据不相等的那个数据。
(1)5.08 m 50800 cm 5080 dm 5080000 cm
(2)6039 dm2 6.039 m2 603900 cm2 60.39 m2
(3)1500 cm 1500 dm 15 m 150 dm
8.修建长城所用的某块砖的尺寸如右图所示。这块长城砖的体积是多少?
40×10×20=8000(cm3)
答:这块长城砖体积是8000cm3。
9.一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是 6 cm、4 cm、5 cm,正方体的棱长是多少厘米?它们的体积相等吗?
6cm
4cm
5cm
?cm
正方体的棱长:(6+5+4)×4÷12=5(cm)
正方体的体积:5×5×5=125(cm3)
长方体的体积:6×5×4=120(cm3)
答:正方体的棱长是5cm,长方体和正方体的体积不相等,正方体的体积大。
10*茶厂工人要将长、宽均为 20 cm,高为 10 cm 的长方体茶盒装入棱长为 30 cm(从里面量)的正方体纸箱,一箱最多能装几盒?怎样才能装下?
20cm
20cm
10cm
求能装几盒,可以用纸箱体积除以茶盒体积吗?
10cm=1dm
3×3×3=27(dm3)
20cm=2dm
30cm=3dm
2×2×1=4 (dm3)
27÷4=6.75(盒)
答:一箱最多能装6盒。
30cm
30cm
30cm
怎样装呢?纸箱棱长30cm,放一个茶盒后就剩10cm……
30cm
正方体纸箱的棱长不是长方体茶盒的长和宽的整数倍,要达到最大盒数,就要合理分配空间。放一个茶盒后就剩10cm,旁边只能再竖着放,这样才可以装下6盒。
10*茶厂工人要将长、宽均为 20 cm,高为 10 cm 的长方体茶盒装入棱长为 30 cm(从里面量)的正方体纸箱,一箱最多能装几盒?怎样才能装下?
11. 一根长方体木料长1.2m、宽6dm、高5dm,现在要将它锯成棱长是2dm的正方体小块,最多可以锯多少个?
1.2m=12dm
12÷2=6(个)
6÷2=3(行)
5÷2=2(层)……1(dm)
6×3×2=36(个)
答:最多可以锯36个。
12.把棱长为1m的正方体木块切割成棱长是1cm的小正方体,这些小正方体一个挨一个地连起来,可以排多长?
1×1×1=1(m )=1000000cm
1×1×1=1(cm )
1000000÷1=1000000(个)
1×1000000=1000000(cm)=10km
答:可以排10km。
13.前进小学修一个长80m、宽50m的长方形操场,先铺15cm厚的三合土,再铺8cm厚的煤渣,需要三合土和煤渣各多少立方米?
答:需要三合土600m ,煤渣320m 。
15cm=0.15m
三合土:80×50×0.15=600(m )
煤渣:80×50×0.08=320(m )
8cm=0.08m
你知道吗?
人们很早就得出长方体、圆柱等形体的体积计算公式。因为它们是河堤、谷仓等的常见形状,而且还有计算体积的需要。
我国古代数学名著《九章算术》中,集中而正确地给出了立体图形的体积计算公式。书中在求底面是正方形的长方体体积时,是这样说的:“方自乘,以高乘之即积尺。”就是说先用边长乘边长得底面积,再乘高就得到长方体的体积。
同学们,这节课你有哪些收获?
单位进率
1.相邻体积单位之间的进率是1000。
1dm =1000cm 1m =1000dm
2.高级单位转换成为低级单位,要乘进率,小数点向右移;低级单位转化成高级单位,要除以进率,小数点向左移。
★ 完成《分层作业》
★★ 在解决有关体积的实际问题时,要看清已知条件的单位是否统一,如果不统一,要先统一单位,再进行计算。动手制作学过单位的进率表。
