第四单元_第01课时_ 比例的意义 (教学课件)-六年级数学下册苏教版(2)(共27张PPT)
文档属性
| 名称 | 第四单元_第01课时_ 比例的意义 (教学课件)-六年级数学下册苏教版(2)(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 16:42:47 | ||
图片预览






文档简介
(共27张PPT)
小学数学·六年级(下)·SJ
第4课时 解比例
2.使学生在观察、比较、思考和交流等活动中,积累数学学习经验,提高分析问题和解决问题的能力。
1.使学生能根据实际问题写出含有未知数的比例,学会用比例的基本性质解比例。
3.培养学生独立思考、合作交流的学习习惯,体验运用所学知识解决数学问题的乐趣,增强数学学习的信心。
应用比例的基本性质解比例。
掌握用比例知识解决实际问题的方法。
养成从数学角度观察现实世界的意识与习惯,发展好奇心和创新意识。
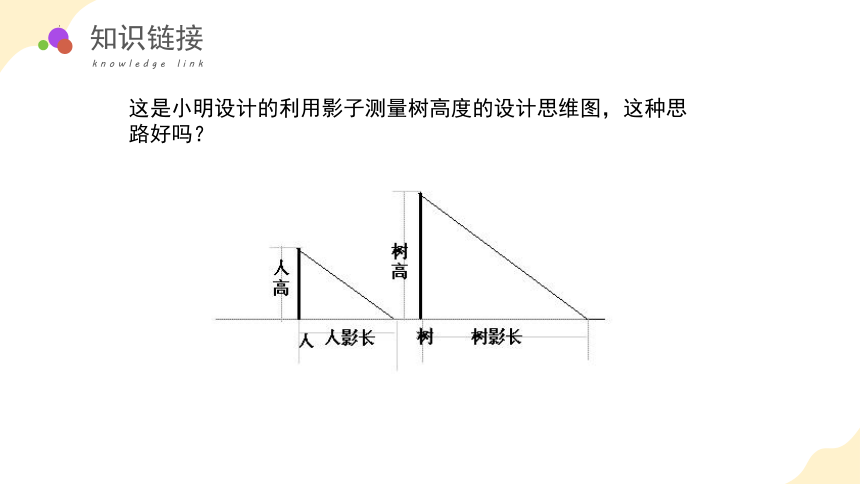
这是小明设计的利用影子测量树高度的设计思维图,这种思路好吗?
解下列简易方程。
×
=
解:
解:
2
= 8 × 9
2
= 72
= 36
=
÷
=
=
= 72 ÷ 2
根据问题生成比例
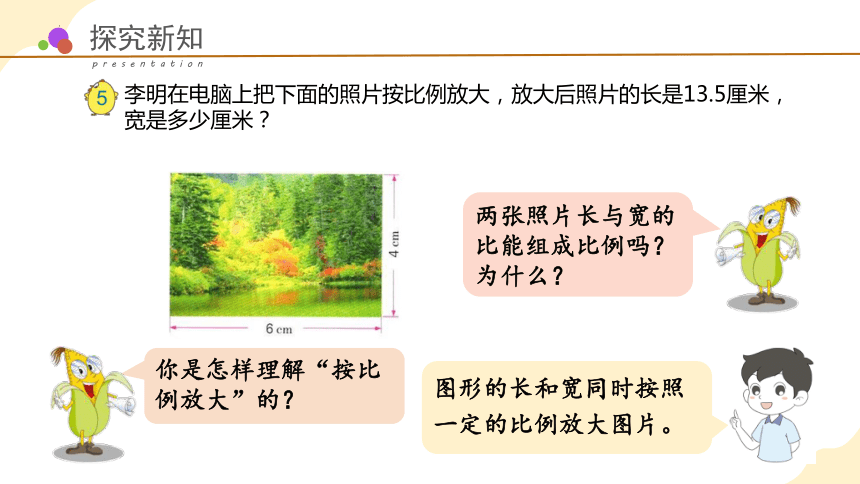
李明在电脑上把下面的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
图形的长和宽同时按照一定的比例放大图片。
你是怎样理解“按比例放大”的?
两张照片长与宽的比能组成比例吗?为什么?
6cm
4cm
放大前
放大后
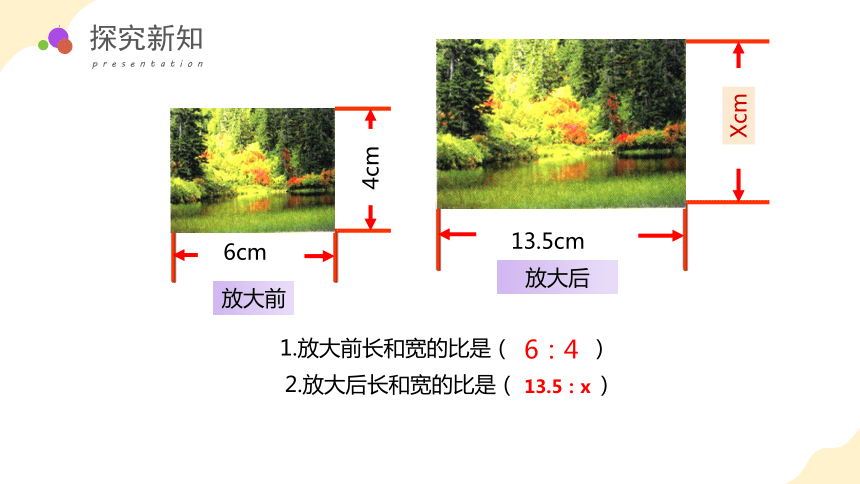
1.放大前长和宽的比是( )
2.放大后长和宽的比是( )
13.5cm
?cm
6:4
13.5:x
Xcm
放大前的长﹕放大前的宽=放大后的长﹕放大后的宽
6
4
13.5
解:设放大后照片的宽是x 厘米
x
﹕
﹕
=
根据按比例放大图形,我们可以这样思考
放大前的长﹕放大后的长=放大前的宽﹕放大后的宽
6
13.5
4
解:设放大后照片的宽是x 厘米
x
﹕
﹕
=
我们还可以这样思考
4﹕X = 6﹕13.5
解:设放大后照片的宽是x 厘米
你还有哪些想法?能写出哪些比例?
X﹕4 = 13.5﹕6
13.5﹕X = 6﹕4
X﹕13.5 = 4﹕6
=
=
可以写出这么多的比例,怎样确保写出的比例是正确的呢?
前后两个比对应的量要一致才行
解比例
李明在电脑上把下面的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
解:设放大后的照片的宽是x厘米。
6∶4=13.5∶x
6x=4×13.5
6x=54
x=9
答:放大后照片的宽是9厘米。
在比例里,两个外项的积等于两个内项的积。
根据比例的基本性质将比例变成方程
6x
=
13.5 ×4
6x
=
54
x
=
9
6﹕4 = 13.5﹕x
6x
=
13.5 ×4
6x
=
54
x
=
9
比例的基本性质
比例转化成方程
等式的性质
求解方程
它们有什么相同的地方?
=
像上面这样求比例中的未知项,叫作解比例。
已知比例中的任意三项,就可以用此方法求出另外一项。
解比例首先要做什么?再怎么做?
首先根据比例的基本性质把比例变成方程,再根据以前学过的解方程的方法求解。
达标检测,巩固练习
1.
2.有四个数4,8,16,x可以组成一个比例,其中x最大是( ),最小是( )。
要使x最小,则可列比例:
4∶x=16∶8
16x=4×8
16x=32
16x÷16=32÷16
x=2
要使x最大,则可列比例:
8∶x=4∶16
解:4x=8×16
4x=128
4x÷4=128÷4
x=32
则x最大是32,最小是2。
32
2
3.狗跑10步与马跑4步的长度相等.照这样计算,狗跑125步,马要跑多少步?(用比例解)
解:设马要跑x步。
10:4=125:x
10x=4×125
10x=500
x=50
答:马要跑50步。
4.(2021.江苏宿迁.期末)有大、小两个圆,大圆的直径是12cm,大圆的周长与小圆的周长的比是3:2,小圆的直径是多少厘米?(用比例解)
解:设小圆的直径是xcm.
3:2=12:x
3x=2×12
3x=24
x=24÷3
x=8
答:小圆的直径是8厘米。
5.(2022.江苏南通.期末)相同质量的冰和水的体积之比是10∶9,一块体积是60立方分米的冰,化成水后的体积是多少?(用比例知识解答)
【分析】根据题意,冰和水的体积之比是10∶9,即它们的体积比值不变,设体积是60立方分米的冰,化成水后的体积是x立方分米,列比例:10∶9=60∶x,解比例,即可解答。
解:设化成水后的体积是x立方分米。
10∶9=60∶x
10x=9×60
10x=540
x=540÷10
x=54
答:化成水后的体积是54立方分米。
6.(2022.江苏南京,期末)A、B两种商品的价格之比为7∶2,如果它们的价格分别上涨60元后,价格之比为5∶2,这两种商品原来的价格各是多少?
【分析】把两种商品的价格之比看作份数,假设一份的价格是x元,那么A的原价相当于7x元,B的原价相当于2x元,它们的价格分别上涨60元后,A的价格变成(7x+60)元,B的价格变成(2x+60),两者之间的价格比为5∶2,根据比例的意义,可列出比例,求解即可。
解:设一份的价格是x元,A的原价是7x元,B的原价是2x元。
(7x+60)∶(2x+60)= 5∶2
(2x+60)×5=(7x+60)×2
10x+60×5=14x+60×2
10x+300=14x+120
14x-10x=300-120
4x=180
x=45
A的原价为:
7×45=315(元)
B的原价为:
2×45=90(元)
答:A商品的原价是315元,
B商品的原价是90元。
这节课你有什么收获?
1
2
求比例中的未知项叫作解比例。
根据比例的基本性质解比例,先把比例转换成两个外项相乘与两个内项相乘的形式(即等式),再通过解方程求出未知项的值。
3
1. 掌握解比例的方法,会根据实际问题用比例来进行解答。
2. 完成《分层作业》
小学数学·六年级(下)·SJ
第4课时 解比例
2.使学生在观察、比较、思考和交流等活动中,积累数学学习经验,提高分析问题和解决问题的能力。
1.使学生能根据实际问题写出含有未知数的比例,学会用比例的基本性质解比例。
3.培养学生独立思考、合作交流的学习习惯,体验运用所学知识解决数学问题的乐趣,增强数学学习的信心。
应用比例的基本性质解比例。
掌握用比例知识解决实际问题的方法。
养成从数学角度观察现实世界的意识与习惯,发展好奇心和创新意识。
这是小明设计的利用影子测量树高度的设计思维图,这种思路好吗?
解下列简易方程。
×
=
解:
解:
2
= 8 × 9
2
= 72
= 36
=
÷
=
=
= 72 ÷ 2
根据问题生成比例
李明在电脑上把下面的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
图形的长和宽同时按照一定的比例放大图片。
你是怎样理解“按比例放大”的?
两张照片长与宽的比能组成比例吗?为什么?
6cm
4cm
放大前
放大后
1.放大前长和宽的比是( )
2.放大后长和宽的比是( )
13.5cm
?cm
6:4
13.5:x
Xcm
放大前的长﹕放大前的宽=放大后的长﹕放大后的宽
6
4
13.5
解:设放大后照片的宽是x 厘米
x
﹕
﹕
=
根据按比例放大图形,我们可以这样思考
放大前的长﹕放大后的长=放大前的宽﹕放大后的宽
6
13.5
4
解:设放大后照片的宽是x 厘米
x
﹕
﹕
=
我们还可以这样思考
4﹕X = 6﹕13.5
解:设放大后照片的宽是x 厘米
你还有哪些想法?能写出哪些比例?
X﹕4 = 13.5﹕6
13.5﹕X = 6﹕4
X﹕13.5 = 4﹕6
=
=
可以写出这么多的比例,怎样确保写出的比例是正确的呢?
前后两个比对应的量要一致才行
解比例
李明在电脑上把下面的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
解:设放大后的照片的宽是x厘米。
6∶4=13.5∶x
6x=4×13.5
6x=54
x=9
答:放大后照片的宽是9厘米。
在比例里,两个外项的积等于两个内项的积。
根据比例的基本性质将比例变成方程
6x
=
13.5 ×4
6x
=
54
x
=
9
6﹕4 = 13.5﹕x
6x
=
13.5 ×4
6x
=
54
x
=
9
比例的基本性质
比例转化成方程
等式的性质
求解方程
它们有什么相同的地方?
=
像上面这样求比例中的未知项,叫作解比例。
已知比例中的任意三项,就可以用此方法求出另外一项。
解比例首先要做什么?再怎么做?
首先根据比例的基本性质把比例变成方程,再根据以前学过的解方程的方法求解。
达标检测,巩固练习
1.
2.有四个数4,8,16,x可以组成一个比例,其中x最大是( ),最小是( )。
要使x最小,则可列比例:
4∶x=16∶8
16x=4×8
16x=32
16x÷16=32÷16
x=2
要使x最大,则可列比例:
8∶x=4∶16
解:4x=8×16
4x=128
4x÷4=128÷4
x=32
则x最大是32,最小是2。
32
2
3.狗跑10步与马跑4步的长度相等.照这样计算,狗跑125步,马要跑多少步?(用比例解)
解:设马要跑x步。
10:4=125:x
10x=4×125
10x=500
x=50
答:马要跑50步。
4.(2021.江苏宿迁.期末)有大、小两个圆,大圆的直径是12cm,大圆的周长与小圆的周长的比是3:2,小圆的直径是多少厘米?(用比例解)
解:设小圆的直径是xcm.
3:2=12:x
3x=2×12
3x=24
x=24÷3
x=8
答:小圆的直径是8厘米。
5.(2022.江苏南通.期末)相同质量的冰和水的体积之比是10∶9,一块体积是60立方分米的冰,化成水后的体积是多少?(用比例知识解答)
【分析】根据题意,冰和水的体积之比是10∶9,即它们的体积比值不变,设体积是60立方分米的冰,化成水后的体积是x立方分米,列比例:10∶9=60∶x,解比例,即可解答。
解:设化成水后的体积是x立方分米。
10∶9=60∶x
10x=9×60
10x=540
x=540÷10
x=54
答:化成水后的体积是54立方分米。
6.(2022.江苏南京,期末)A、B两种商品的价格之比为7∶2,如果它们的价格分别上涨60元后,价格之比为5∶2,这两种商品原来的价格各是多少?
【分析】把两种商品的价格之比看作份数,假设一份的价格是x元,那么A的原价相当于7x元,B的原价相当于2x元,它们的价格分别上涨60元后,A的价格变成(7x+60)元,B的价格变成(2x+60),两者之间的价格比为5∶2,根据比例的意义,可列出比例,求解即可。
解:设一份的价格是x元,A的原价是7x元,B的原价是2x元。
(7x+60)∶(2x+60)= 5∶2
(2x+60)×5=(7x+60)×2
10x+60×5=14x+60×2
10x+300=14x+120
14x-10x=300-120
4x=180
x=45
A的原价为:
7×45=315(元)
B的原价为:
2×45=90(元)
答:A商品的原价是315元,
B商品的原价是90元。
这节课你有什么收获?
1
2
求比例中的未知项叫作解比例。
根据比例的基本性质解比例,先把比例转换成两个外项相乘与两个内项相乘的形式(即等式),再通过解方程求出未知项的值。
3
1. 掌握解比例的方法,会根据实际问题用比例来进行解答。
2. 完成《分层作业》
