第四单元+第2课时 比例的意义(教学课件)-六年级数学下册同步高效课堂系列+苏教版 (1)(共26张PPT)
文档属性
| 名称 | 第四单元+第2课时 比例的意义(教学课件)-六年级数学下册同步高效课堂系列+苏教版 (1)(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 16:58:25 | ||
图片预览





文档简介
(共26张PPT)
小学数学·六年级(下)·SJ
第2课时 比例的意义
2.在观察、比较和交流的过程中,培养学生自主探究、分析、概括能力。
1.使学生理解并掌握比例的意义,学会应用比例的意义判断两个比能否组成比例。
3.感受比例在生活中的作用,提高数学应用的意识和实践能力,激发数学学习的兴趣。
理解比例的意义,能正确判断两个比能否组成比例。
掌握判断两个比是否能组成比例的方法。
培养初步的形象思维和逻辑思维能力,发展空间观念。
观看视频,思考视频中的问题。
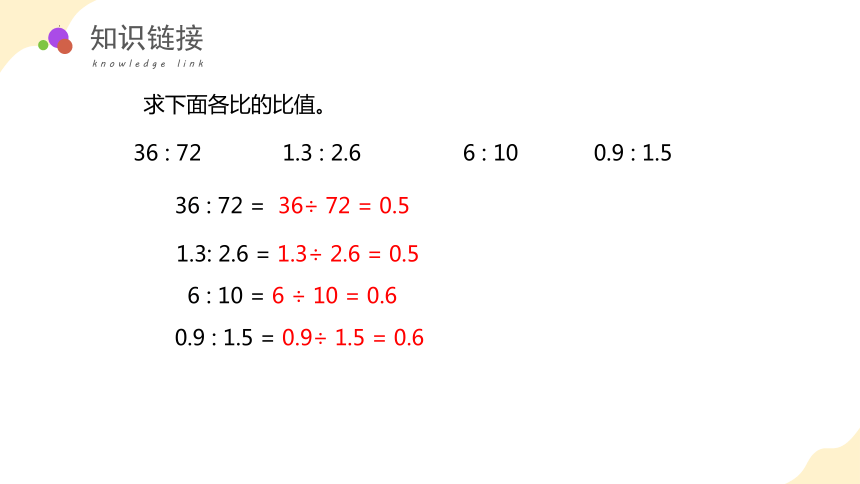
求下面各比的比值。
36 : 72
1.3 : 2.6
6 : 10
36 : 72 = 36÷ 72 = 0.5
6 : 10 = 6 ÷ 10 = 0.6
1.3: 2.6 = 1.3÷ 2.6 = 0.5
0.9 : 1.5
0.9 : 1.5 = 0.9÷ 1.5 = 0.6
比例的认识
3
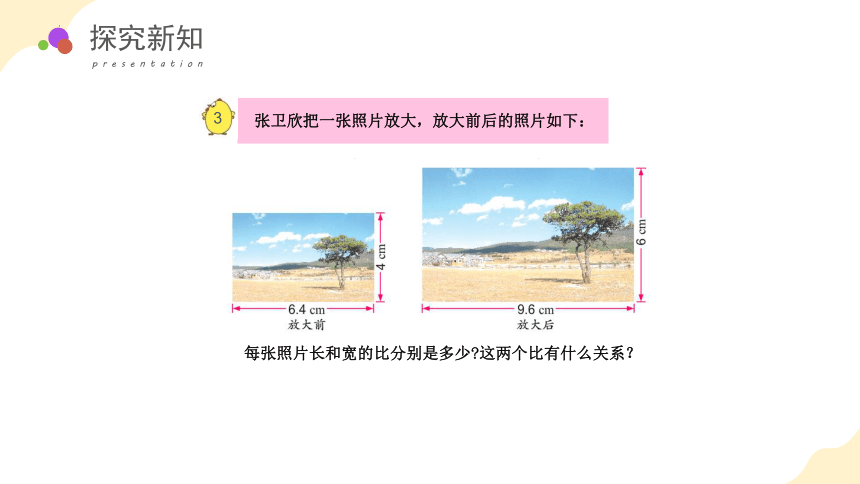
张卫欣把一张照片放大,放大前后的照片如下:
每张照片长和宽的比分别是多少 这两个比有什么关系?
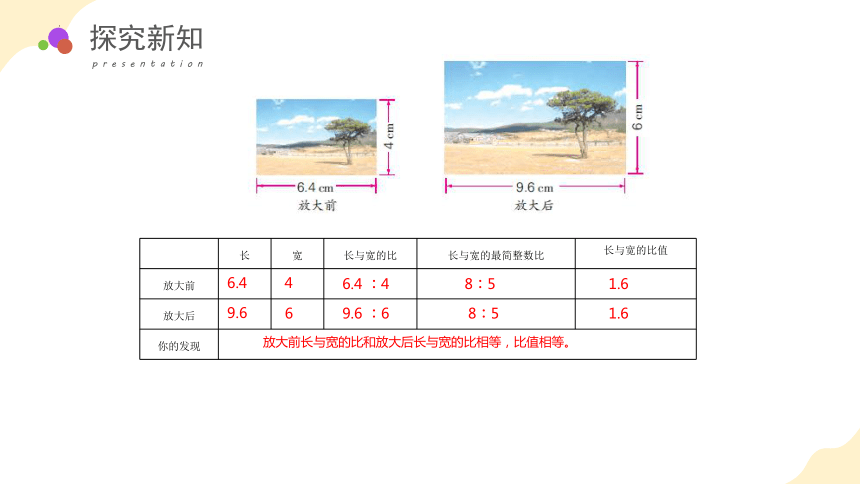
长 宽 长与宽的比 长与宽的最简整数比 长与宽的比值
放大前
放大后
你的发现 6.4
6.4 ︰4
4
8︰5
8︰5
1.6
1.6
9.6
6
9.6 ︰6
放大前长与宽的比和放大后长与宽的比相等,比值相等。
放大后照片长和宽的比是9.6 :6。
放大前照片长和宽的比是6.4:4。
这两个比化简后都是8:5,它们的比值都是1.6。
或
这两个比相等,我们可以用什么式子来表示?
表示两个比相等的式子叫作比例。
判断两个比能否组成比例
分别写出照片放大后与放大前长的比和宽的比,这两个比也能组成比例吗?
9.6 : 6.4
6 : 4
放大后与放大前
长的比
放大后与放大前
宽的比
9.6 : 6.4 = 3 : 2
6 : 4= 3 : 2
这两个比能组成比例。
9.6 : 6.4=6 : 4
9.6 : 6.4 =
3
2
6 : 4 =
3
2
想一想:
怎样判断两个比是否能组成比例
如果两个比化简后的比相同或它们的比值相等,这两个
比就能组成比例。
比 4︰6
比例 2︰3=4︰6
比和比例有什么区别?
由两个数组成,是一个式子,
表示两个数相除。
由四个数组成,是一个等式。
表示两个比相等的式子。
达标检测,巩固练习
1.判断下面哪个比能与 :4组成比例。
(1)5:4 (2)20:1
(3)1:20 (4)5:
4
1
√
2.下面各表中相对应的两个数量的比能否组成比例?如果能组成比例,把组成的比例写出来。
4 :240 =
6 :360 =
所以它们能组成比例。 4 :240 =6 :360
因为
比值相同,
3.因为3a=4b,所以( )。 A.a∶b=3∶4 B.a∶4=3∶b
C.b∶3=a∶4 D.3∶a=4∶b
选项A:因为a∶b=3∶4,所以4a=3b,与题意不符合;
选项B:因为a∶4=3∶b,所以ab=12,与题意不符合;
选项C:因为b∶3=a∶4,所以3a=4b,与题意符合;
选项D:3∶a=4∶b,所以4a=3b,与题意不符合。
比例的基本性质:两个内项的乘积等于两个外项的乘积。
C
4.(2021.江苏景德镇.期末)已知比例5∶( )=( )∶0.8,组成这个比例的两个比的比值都是2,这个比例是( )。
【分析】先用5除以2,求出等号左边的内项;再用2乘0.8,求出等号右边的内项,然后写出这个比例式即可。
5∶2.5=1.6∶0.8
5÷2=2.5,2×0.8=1.6
这个比例式为5∶2.5=1.6∶0.8。
5.(2022.江苏无锡.期末)师傅加工50个零件需要3小时,那么加工80个这样的零件,需要多少小时?
因为师傅加工50的零件需要3小时,问加工80个这样的零件,需要多少小时,可以设需要x小时,50:3表示师傅每个小时加工的个数,80:x也表示师傅每个小时加工的个数,据此可以列出比例50:3=80:x,然后算出x即可.
解:设需要x小时.
50:3=80:x
50x=3×80
x=4.8
答:需要4.8小时.
6.(2022.江苏苏州.期末)把下面的等式改写成比例式.
(1)4×50=10×20 (2)4x=7y
把4和50作为外项,10和20作为内项,写出比例:
4∶10=20∶50
把4和x作为外项,x和7作为内项,写出比例:
4∶7=y∶x
这节课你有什么收获?
1
2
表示两个比相等的式子叫作比例。
能组成比例的两个比,它们的比值相等。
1. 理解比例的意义,会判断两个比能否组成比例;
2. 完成《分层作业》
小学数学·六年级(下)·SJ
第2课时 比例的意义
2.在观察、比较和交流的过程中,培养学生自主探究、分析、概括能力。
1.使学生理解并掌握比例的意义,学会应用比例的意义判断两个比能否组成比例。
3.感受比例在生活中的作用,提高数学应用的意识和实践能力,激发数学学习的兴趣。
理解比例的意义,能正确判断两个比能否组成比例。
掌握判断两个比是否能组成比例的方法。
培养初步的形象思维和逻辑思维能力,发展空间观念。
观看视频,思考视频中的问题。
求下面各比的比值。
36 : 72
1.3 : 2.6
6 : 10
36 : 72 = 36÷ 72 = 0.5
6 : 10 = 6 ÷ 10 = 0.6
1.3: 2.6 = 1.3÷ 2.6 = 0.5
0.9 : 1.5
0.9 : 1.5 = 0.9÷ 1.5 = 0.6
比例的认识
3
张卫欣把一张照片放大,放大前后的照片如下:
每张照片长和宽的比分别是多少 这两个比有什么关系?
长 宽 长与宽的比 长与宽的最简整数比 长与宽的比值
放大前
放大后
你的发现 6.4
6.4 ︰4
4
8︰5
8︰5
1.6
1.6
9.6
6
9.6 ︰6
放大前长与宽的比和放大后长与宽的比相等,比值相等。
放大后照片长和宽的比是9.6 :6。
放大前照片长和宽的比是6.4:4。
这两个比化简后都是8:5,它们的比值都是1.6。
或
这两个比相等,我们可以用什么式子来表示?
表示两个比相等的式子叫作比例。
判断两个比能否组成比例
分别写出照片放大后与放大前长的比和宽的比,这两个比也能组成比例吗?
9.6 : 6.4
6 : 4
放大后与放大前
长的比
放大后与放大前
宽的比
9.6 : 6.4 = 3 : 2
6 : 4= 3 : 2
这两个比能组成比例。
9.6 : 6.4=6 : 4
9.6 : 6.4 =
3
2
6 : 4 =
3
2
想一想:
怎样判断两个比是否能组成比例
如果两个比化简后的比相同或它们的比值相等,这两个
比就能组成比例。
比 4︰6
比例 2︰3=4︰6
比和比例有什么区别?
由两个数组成,是一个式子,
表示两个数相除。
由四个数组成,是一个等式。
表示两个比相等的式子。
达标检测,巩固练习
1.判断下面哪个比能与 :4组成比例。
(1)5:4 (2)20:1
(3)1:20 (4)5:
4
1
√
2.下面各表中相对应的两个数量的比能否组成比例?如果能组成比例,把组成的比例写出来。
4 :240 =
6 :360 =
所以它们能组成比例。 4 :240 =6 :360
因为
比值相同,
3.因为3a=4b,所以( )。 A.a∶b=3∶4 B.a∶4=3∶b
C.b∶3=a∶4 D.3∶a=4∶b
选项A:因为a∶b=3∶4,所以4a=3b,与题意不符合;
选项B:因为a∶4=3∶b,所以ab=12,与题意不符合;
选项C:因为b∶3=a∶4,所以3a=4b,与题意符合;
选项D:3∶a=4∶b,所以4a=3b,与题意不符合。
比例的基本性质:两个内项的乘积等于两个外项的乘积。
C
4.(2021.江苏景德镇.期末)已知比例5∶( )=( )∶0.8,组成这个比例的两个比的比值都是2,这个比例是( )。
【分析】先用5除以2,求出等号左边的内项;再用2乘0.8,求出等号右边的内项,然后写出这个比例式即可。
5∶2.5=1.6∶0.8
5÷2=2.5,2×0.8=1.6
这个比例式为5∶2.5=1.6∶0.8。
5.(2022.江苏无锡.期末)师傅加工50个零件需要3小时,那么加工80个这样的零件,需要多少小时?
因为师傅加工50的零件需要3小时,问加工80个这样的零件,需要多少小时,可以设需要x小时,50:3表示师傅每个小时加工的个数,80:x也表示师傅每个小时加工的个数,据此可以列出比例50:3=80:x,然后算出x即可.
解:设需要x小时.
50:3=80:x
50x=3×80
x=4.8
答:需要4.8小时.
6.(2022.江苏苏州.期末)把下面的等式改写成比例式.
(1)4×50=10×20 (2)4x=7y
把4和50作为外项,10和20作为内项,写出比例:
4∶10=20∶50
把4和x作为外项,x和7作为内项,写出比例:
4∶7=y∶x
这节课你有什么收获?
1
2
表示两个比相等的式子叫作比例。
能组成比例的两个比,它们的比值相等。
1. 理解比例的意义,会判断两个比能否组成比例;
2. 完成《分层作业》
