容积和容积单位(课件)-2023-2024学年五年级下册数学人教版(共54张PPT)
文档属性
| 名称 | 容积和容积单位(课件)-2023-2024学年五年级下册数学人教版(共54张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 24.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 17:05:19 | ||
图片预览










文档简介
(共54张PPT)
容积和容积单位
(1)
这些物体都能容纳其他物体。
一、联系实际引入新知
你们见过这些物体吗?它们有什么共同点?
像太空舱、粮仓、油桶、盒子等所能容纳物体的体积,通常叫作它们的容积。
生活中哪些物品可以装东西?请你说一说,什么是它们的容积?
二、自主探究,建立容积概念
仓 库
判断对错。
(1)一辆货车车厢所能容纳货物的体积,就是
这辆货车车厢的容积。 ( )
(2)一个药瓶里装了半瓶药水,这些药水的体
积就是药瓶的容积。 ( )
(3)有两个体积一样大的箱子,它们的容积一
定同样大。 ( )
√
×
×
三、实践操作,认识容积单位
计量容积一般用体积单位。
箱子的容积约是8dm3
一节车箱的
容积约是
350m3
计量液体的体积,常用升和
毫升来表示。
净含量5升
净含量355毫升
计量容积一般用体积单位。
计量液体(如水、油等)的体积常用容积单位
升(L)和毫升(mL)。
1.初步认识容积单位。
2.通过观察比较,建立1升、1毫升和100毫升的表象。
这是10ml药水瓶,想一想1ml是多少,比一比。
250ml果汁是这么多,100ml大约是多少?
1L相当于几个250ml?
测量液体的多少,有专门的测量工具,如量筒或烧杯:
量筒
量杯
量筒
烧杯
量筒的介绍和使用方法
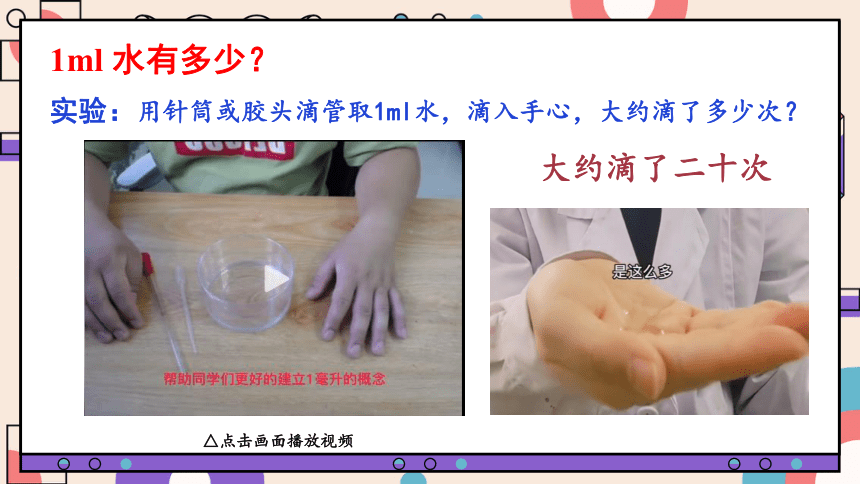
1ml 水有多少?
大约滴了二十次
△点击画面播放视频
实验:用针筒或胶头滴管取1ml水,滴入手心,大约滴了多少次?
1ml
1cm3
将1ml的液体倒入1cm3的正方体容器中,正好装满。
1 mL=1 cm3
实验:将1L水倒入棱长为1dm的正方体盒子,你有什么发现?
△点击画面播放视频
1 L=1 dm3
=1000 cm3
1L 水有多少?
实验:在100 mL的量筒中装入100毫升水,倒入1000毫升的量
杯中,你有什么发现?
倒( )次正好倒够1000毫升水。
10
100 mL 水有多少?
3.掌握升与毫升之间的进率。
1 L=1 dm3
1 mL=1 cm3
1 L=1000 mL
容积单位和体积单位有这样的关系:
知道为什么“1 L=1000 mL”吗?
(1)说一说,哪些物品上标有毫升、升。
4.演示活动,感知容积单位的实际大小。
(2)估计一下:一纸杯水大约有多少毫升?
几杯水大约是 1 L?
品尝杯
一次性纸杯
豆浆杯
奶茶杯
55ml
250ml
330ml
500ml
一个长方体的油箱,从里面量长 5 dm,宽 4 dm,高 2 dm。这个油箱可以装多少升油?
5×4×2=40(dm3)
40 dm3=40 L
答: 这个油箱可以装汽油 40 L。
四、迁移类推,掌握容积计算方法
物体的体积和容积有哪些相同的地方和不同的地方?
相同点:计算方法相同。
不同点:体积要从物体的外面量长、宽、高,
容积要从物体的里面量长、宽、高。
设法求出下面两种物体的体积。
橡皮泥
土豆
你从图中读到了什么信息?要解决什么问题?
求不规则物体的体积。
这些不规则物体的体积怎么计算呢?你有什么好办法吗?
橡皮泥
土豆
(小组讨论,稍后汇报,集体评议。)
根据你们刚才的方法,我们一起来动手做实验,同学们仔细观察,填写好实验报告单。
所测物体 测量方法 所需数据 结论
实验报告单
橡皮泥
①研究橡皮泥体积的计算方法。
捏压
a.求橡皮泥的体积用什么方法比较好?
b.计算这个长方体(或正方体),需要知道哪些数据?
c.长方体的体积跟不规则的橡皮泥的体积有什么关系呢?
“形变积等”
②研究土豆体积的计算方法。
b.求土豆的体积用什么方法比较好?
a.土豆也能捏压成长方体吗?
(不行)
排水法
排水法
水的体积
是____mL。
水和土豆的
体积是____cm3。
250
400
土豆的体积:400-250=150(cm3)
答:土豆的体积是150 cm3 。
所测物体 测量方法 所需数据 结论
实验报告单
填写报告单。
橡皮泥
捏压法
长、宽、高
土豆
排水法
原来水的体积,
水面上升后的总体积;
长×宽×高
水面上升后的总体积
-原来水的体积;
我们用不同的方法求出了橡皮泥、土豆的体积,你喜欢哪种方法?为什么?
排水法
橡皮泥
捏压
在用排水法测量时,为什么上升的水的体积就是土豆的体积?
排水法
等于土豆的体积
不论是用捏压的方法、还是排水法,都是
不规则物体
转化
规则物体
用“排水法”求不规则物体的体积需要记录哪些数据?
需要记录水里未放物体时的体积以及放入不规则物体后总的体积。
还要注意哪些问题?
要使物体全部浸入水中。
五、巩固深化
1.在横线上填写合适的容积单位。
一瓶墨水约 50____
一瓶洗手液约500___
“奋斗者”号载人潜水器载人舱的容积为3___
mL
mL
一台冰箱容积约229___
m3
L
【选自教材P40 练习九 第1题】
4 L=______mL 82 cm3=_____mL 4800 mL=_____L
2.4 L=______mL 35 dm3=______mL
500 mL=_____L
8.04 dm3=_____L=_______mL
785 mL=_____cm3=______dm3
2.
4000
4.8
82
0.5
35000
2400
8.04
8040
785
0.785
3. 下图中珊瑚石的体积是多少?
方法一: 8×8×( 7-6 )=64(cm3)
方法二: 8×8× 7- 8×8× 6 =64(cm3)
答:珊瑚石的体积是 64 cm3。
【选自教材P41 练习九 第7题】
4. 将一块假山石放入一个盛有水的、底面积为 51 dm2 的长方体鱼缸中,完全浸没后,水面上升了 3 cm。这个假山石的体积有多大?
51×0.3=15.3(dm3)
3 cm=0.3 dm
答:假山石的体积为15.3dm3。
【选自教材P41 练习九 第8题】
1
判断:物体的体积就是它的容积。 ( )
×
容积指的是物体内部空间的大小, 体积指的是物体自身所占空间的大小。一般情况下,物体的体积大于它的容积。
2
1L=( )mL
1000cm =( )mL
1L=( )dm
填空题。
1升=1000毫升
1升=1立方分米
1毫升=1立方厘米
1000
1
1000
3
一个长8米、宽4米、深3米的长方体蓄水池,它最多能容纳多少升水?
8×4×3=96(立方米)
96立方米=96000立方分米=96000升
答:它最多能容纳96000升水。
4
一个棱长是30厘米的正方体油桶装满汽油,如果每升汽油重0.88千克,那么这桶汽油重多少千克?
30×30×30=27000(立方厘米)
27000立方厘米=27升
0.88×27=23.76(千克)
答:这桶汽油重23.76千克。
六、课堂小结
这节课学习了什么?你们有什么收获?
像太空舱、粮仓、油桶、盒子等所能容纳物体的体积,通常叫作它们的容积。
计量容积一般用体积单位。
计量液体(如水、油等)的体积常用容积单位
升(L)和毫升(mL)。
1 L=1 dm3
1 mL=1 cm3
1 L=1000 mL
捏压:转化成长方体或正方体
排水法: 把物体完全浸没在水里,上升部分水
的体积就是不规则物体的体积。
不规则物体
转化
规则物体
七、作业设计
完成课时练本课时内容及以下练习题
一、在横线上填上合适的容积单位。
10_____
500_____
2.5_____
mL
mL
L
1. 1个水壶能装水2.5 L。“2.5L”指的是这个水壶的
( )。
A.体积 B.表面积 C.容积
2. 一个木箱能容纳40dm3的物体,这个木箱的体积
( )40dm3
A.大于 B.等于 C.小于
C
A
二、选一选。(将正确答案的序号填在括号里)
3.两个容器的体积相等,它们的容积( )。
A.可能不相等 B.一定不相等 C.一定相等
4.一个长方体水箱从里面量长0.6 m,宽0.4 m,高0.3m,
这个水箱可以装水( )L。
A.0.027 B.0.72 C.72
C
A
容积和容积单位
(1)
这些物体都能容纳其他物体。
一、联系实际引入新知
你们见过这些物体吗?它们有什么共同点?
像太空舱、粮仓、油桶、盒子等所能容纳物体的体积,通常叫作它们的容积。
生活中哪些物品可以装东西?请你说一说,什么是它们的容积?
二、自主探究,建立容积概念
仓 库
判断对错。
(1)一辆货车车厢所能容纳货物的体积,就是
这辆货车车厢的容积。 ( )
(2)一个药瓶里装了半瓶药水,这些药水的体
积就是药瓶的容积。 ( )
(3)有两个体积一样大的箱子,它们的容积一
定同样大。 ( )
√
×
×
三、实践操作,认识容积单位
计量容积一般用体积单位。
箱子的容积约是8dm3
一节车箱的
容积约是
350m3
计量液体的体积,常用升和
毫升来表示。
净含量5升
净含量355毫升
计量容积一般用体积单位。
计量液体(如水、油等)的体积常用容积单位
升(L)和毫升(mL)。
1.初步认识容积单位。
2.通过观察比较,建立1升、1毫升和100毫升的表象。
这是10ml药水瓶,想一想1ml是多少,比一比。
250ml果汁是这么多,100ml大约是多少?
1L相当于几个250ml?
测量液体的多少,有专门的测量工具,如量筒或烧杯:
量筒
量杯
量筒
烧杯
量筒的介绍和使用方法
1ml 水有多少?
大约滴了二十次
△点击画面播放视频
实验:用针筒或胶头滴管取1ml水,滴入手心,大约滴了多少次?
1ml
1cm3
将1ml的液体倒入1cm3的正方体容器中,正好装满。
1 mL=1 cm3
实验:将1L水倒入棱长为1dm的正方体盒子,你有什么发现?
△点击画面播放视频
1 L=1 dm3
=1000 cm3
1L 水有多少?
实验:在100 mL的量筒中装入100毫升水,倒入1000毫升的量
杯中,你有什么发现?
倒( )次正好倒够1000毫升水。
10
100 mL 水有多少?
3.掌握升与毫升之间的进率。
1 L=1 dm3
1 mL=1 cm3
1 L=1000 mL
容积单位和体积单位有这样的关系:
知道为什么“1 L=1000 mL”吗?
(1)说一说,哪些物品上标有毫升、升。
4.演示活动,感知容积单位的实际大小。
(2)估计一下:一纸杯水大约有多少毫升?
几杯水大约是 1 L?
品尝杯
一次性纸杯
豆浆杯
奶茶杯
55ml
250ml
330ml
500ml
一个长方体的油箱,从里面量长 5 dm,宽 4 dm,高 2 dm。这个油箱可以装多少升油?
5×4×2=40(dm3)
40 dm3=40 L
答: 这个油箱可以装汽油 40 L。
四、迁移类推,掌握容积计算方法
物体的体积和容积有哪些相同的地方和不同的地方?
相同点:计算方法相同。
不同点:体积要从物体的外面量长、宽、高,
容积要从物体的里面量长、宽、高。
设法求出下面两种物体的体积。
橡皮泥
土豆
你从图中读到了什么信息?要解决什么问题?
求不规则物体的体积。
这些不规则物体的体积怎么计算呢?你有什么好办法吗?
橡皮泥
土豆
(小组讨论,稍后汇报,集体评议。)
根据你们刚才的方法,我们一起来动手做实验,同学们仔细观察,填写好实验报告单。
所测物体 测量方法 所需数据 结论
实验报告单
橡皮泥
①研究橡皮泥体积的计算方法。
捏压
a.求橡皮泥的体积用什么方法比较好?
b.计算这个长方体(或正方体),需要知道哪些数据?
c.长方体的体积跟不规则的橡皮泥的体积有什么关系呢?
“形变积等”
②研究土豆体积的计算方法。
b.求土豆的体积用什么方法比较好?
a.土豆也能捏压成长方体吗?
(不行)
排水法
排水法
水的体积
是____mL。
水和土豆的
体积是____cm3。
250
400
土豆的体积:400-250=150(cm3)
答:土豆的体积是150 cm3 。
所测物体 测量方法 所需数据 结论
实验报告单
填写报告单。
橡皮泥
捏压法
长、宽、高
土豆
排水法
原来水的体积,
水面上升后的总体积;
长×宽×高
水面上升后的总体积
-原来水的体积;
我们用不同的方法求出了橡皮泥、土豆的体积,你喜欢哪种方法?为什么?
排水法
橡皮泥
捏压
在用排水法测量时,为什么上升的水的体积就是土豆的体积?
排水法
等于土豆的体积
不论是用捏压的方法、还是排水法,都是
不规则物体
转化
规则物体
用“排水法”求不规则物体的体积需要记录哪些数据?
需要记录水里未放物体时的体积以及放入不规则物体后总的体积。
还要注意哪些问题?
要使物体全部浸入水中。
五、巩固深化
1.在横线上填写合适的容积单位。
一瓶墨水约 50____
一瓶洗手液约500___
“奋斗者”号载人潜水器载人舱的容积为3___
mL
mL
一台冰箱容积约229___
m3
L
【选自教材P40 练习九 第1题】
4 L=______mL 82 cm3=_____mL 4800 mL=_____L
2.4 L=______mL 35 dm3=______mL
500 mL=_____L
8.04 dm3=_____L=_______mL
785 mL=_____cm3=______dm3
2.
4000
4.8
82
0.5
35000
2400
8.04
8040
785
0.785
3. 下图中珊瑚石的体积是多少?
方法一: 8×8×( 7-6 )=64(cm3)
方法二: 8×8× 7- 8×8× 6 =64(cm3)
答:珊瑚石的体积是 64 cm3。
【选自教材P41 练习九 第7题】
4. 将一块假山石放入一个盛有水的、底面积为 51 dm2 的长方体鱼缸中,完全浸没后,水面上升了 3 cm。这个假山石的体积有多大?
51×0.3=15.3(dm3)
3 cm=0.3 dm
答:假山石的体积为15.3dm3。
【选自教材P41 练习九 第8题】
1
判断:物体的体积就是它的容积。 ( )
×
容积指的是物体内部空间的大小, 体积指的是物体自身所占空间的大小。一般情况下,物体的体积大于它的容积。
2
1L=( )mL
1000cm =( )mL
1L=( )dm
填空题。
1升=1000毫升
1升=1立方分米
1毫升=1立方厘米
1000
1
1000
3
一个长8米、宽4米、深3米的长方体蓄水池,它最多能容纳多少升水?
8×4×3=96(立方米)
96立方米=96000立方分米=96000升
答:它最多能容纳96000升水。
4
一个棱长是30厘米的正方体油桶装满汽油,如果每升汽油重0.88千克,那么这桶汽油重多少千克?
30×30×30=27000(立方厘米)
27000立方厘米=27升
0.88×27=23.76(千克)
答:这桶汽油重23.76千克。
六、课堂小结
这节课学习了什么?你们有什么收获?
像太空舱、粮仓、油桶、盒子等所能容纳物体的体积,通常叫作它们的容积。
计量容积一般用体积单位。
计量液体(如水、油等)的体积常用容积单位
升(L)和毫升(mL)。
1 L=1 dm3
1 mL=1 cm3
1 L=1000 mL
捏压:转化成长方体或正方体
排水法: 把物体完全浸没在水里,上升部分水
的体积就是不规则物体的体积。
不规则物体
转化
规则物体
七、作业设计
完成课时练本课时内容及以下练习题
一、在横线上填上合适的容积单位。
10_____
500_____
2.5_____
mL
mL
L
1. 1个水壶能装水2.5 L。“2.5L”指的是这个水壶的
( )。
A.体积 B.表面积 C.容积
2. 一个木箱能容纳40dm3的物体,这个木箱的体积
( )40dm3
A.大于 B.等于 C.小于
C
A
二、选一选。(将正确答案的序号填在括号里)
3.两个容器的体积相等,它们的容积( )。
A.可能不相等 B.一定不相等 C.一定相等
4.一个长方体水箱从里面量长0.6 m,宽0.4 m,高0.3m,
这个水箱可以装水( )L。
A.0.027 B.0.72 C.72
C
A
