5.4统计与概率的应用 同步练习(含解析)
文档属性
| 名称 | 5.4统计与概率的应用 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 00:00:00 | ||
图片预览


文档简介
5.4统计与概率的应用同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,正六边形的顶点是正六边形的对角线的交点.在正六边形内部任取一点,则该点取自正六边形内的概率为( )
A. B. C. D.
2.某产品的设计长度为,规定误差不超过为合格品.今对一批产品进行测量,测量结果如下表:
长度 以下 以上
件数 5 68 7
则这批产品的不合格率为( )
A. B. C. D.
3.“社保”已经走入了我们的生活,它包括养老保险、医疗保险、失业保险、工伤保险、生育保险.全年支出最重要的三项分别为养老保险、失业保险、工伤保险三项,下图是近五年三项社会保险基金的收支情况,下列说法中错误的是( )
A.三项社会保险基金在2020年以前收入为逐年递增
B.三项社会保险基金在2016~2019年间收支并未出现“赤字”
C.2020年三项社会保险基金收入合计50666亿元,比上年减少8464亿元,约减少14.3%
D.2020年三项社会保险基金支出合计57580亿元,比上年增加3088亿元,约增长6.7%
4.数据3.2,3.4,3.8,4.2,4.3,4.5,x,6.6的第65百分位数是4.5,则实数x的取值范围是( )
A. B. C. D.
5.在北京消费季活动中,某商场为促销举行购物抽奖活动,规定购物消费每满200元就可以参加一次抽奖活动,中奖的概率为.那么以下理解正确的是( )
A.某顾客抽奖10次,一定能中奖1次
B.某顾客抽奖10次,可能1次也没中奖
C.某顾客消费210元,一定不能中奖
D.某顾客消费1000元,至少能中奖1次
6.某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分,分值高者为优),分别绘制了如图所示的六维能力雷达图,图中点A表示甲的创造力指标值为4,点B表示乙的空间能力指标值为3,则下列叙述错误的是( )
A.甲的六大能力中推理能力最差 B.甲的创造力优于观察能力
C.乙的计算能力优于甲的计算能力 D.乙的六大能力整体水平低于甲
7.根据某市疾控中心的健康监测,该市在校中学生的近视率约为78.7%.某眼镜厂商要到中学给近视学生配送滴眼液,每人一瓶,已知该校学生总数为600人,则眼镜商应带滴眼液的瓶数为( )
A.600 B.787 C.不少于473 D.不多于473
8.从一群正在做游戏的小孩中抽出人,一人分一个苹果后,让他们返回继续游戏,一会儿,再从中任取人,发现其中有个小孩曾分过苹果,估计一共有小孩( )
A.人 B.人 C.人 D.人
二、多选题
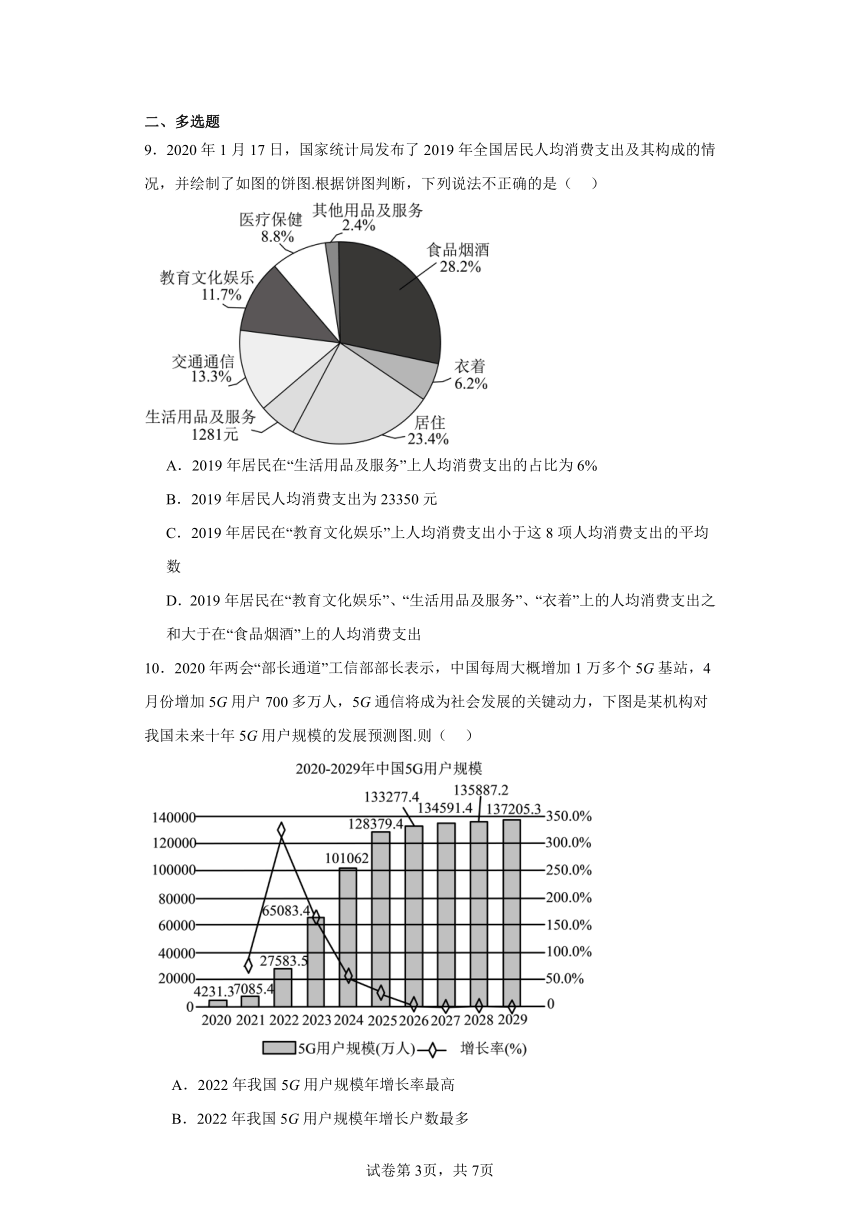
9.2020年1月17日,国家统计局发布了2019年全国居民人均消费支出及其构成的情况,并绘制了如图的饼图.根据饼图判断,下列说法不正确的是( )
A.2019年居民在“生活用品及服务”上人均消费支出的占比为6%
B.2019年居民人均消费支出为23350元
C.2019年居民在“教育文化娱乐”上人均消费支出小于这8项人均消费支出的平均数
D.2019年居民在“教育文化娱乐”、“生活用品及服务”、“衣着”上的人均消费支出之和大于在“食品烟酒”上的人均消费支出
10.2020年两会“部长通道”工信部部长表示,中国每周大概增加1万多个5G基站,4月份增加5G用户700多万人,5G通信将成为社会发展的关键动力,下图是某机构对我国未来十年5G用户规模的发展预测图.则( )
A.2022年我国5G用户规模年增长率最高
B.2022年我国5G用户规模年增长户数最多
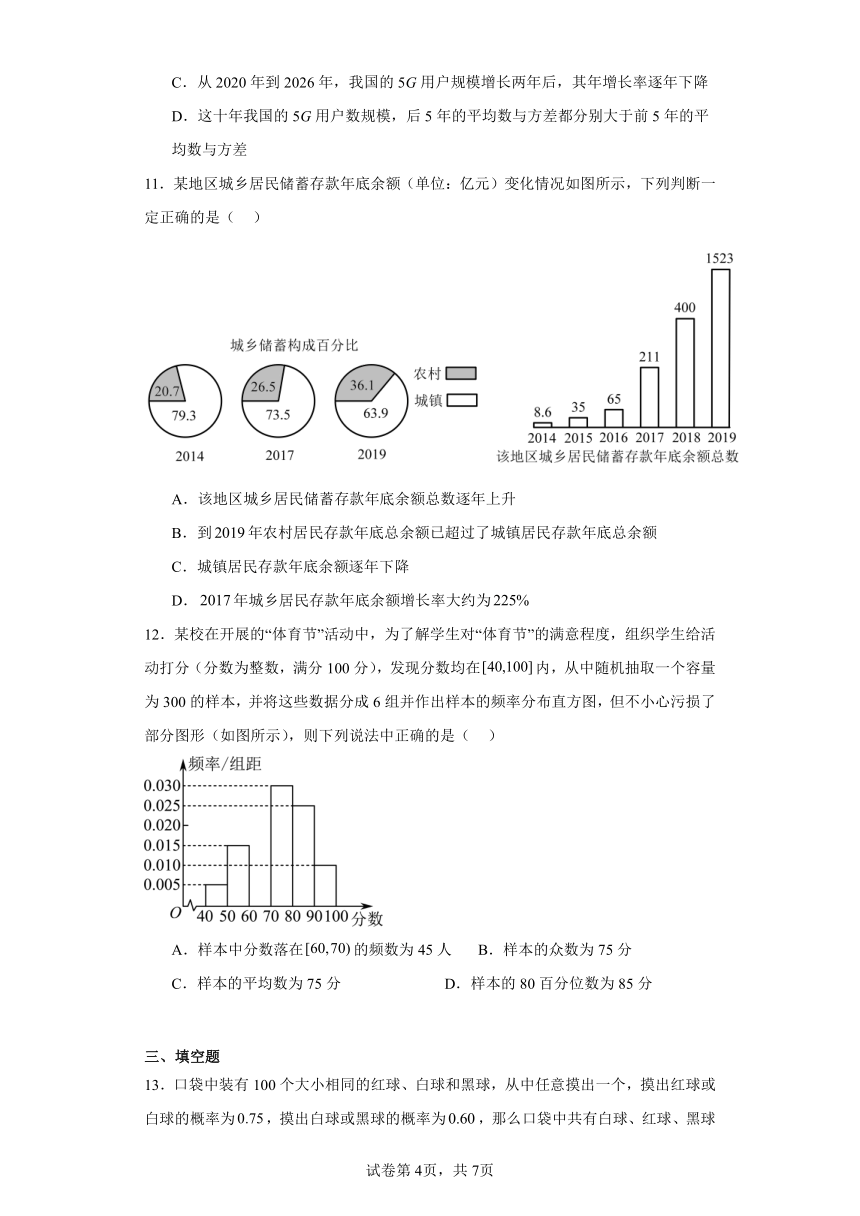
C.从2020年到2026年,我国的5G用户规模增长两年后,其年增长率逐年下降
D.这十年我国的5G用户数规模,后5年的平均数与方差都分别大于前5年的平均数与方差
11.某地区城乡居民储蓄存款年底余额(单位:亿元)变化情况如图所示,下列判断一定正确的是( )
A.该地区城乡居民储蓄存款年底余额总数逐年上升
B.到年农村居民存款年底总余额已超过了城镇居民存款年底总余额
C.城镇居民存款年底余额逐年下降
D.年城乡居民存款年底余额增长率大约为
12.某校在开展的“体育节”活动中,为了解学生对“体育节”的满意程度,组织学生给活动打分(分数为整数,满分100分),发现分数均在内,从中随机抽取一个容量为300的样本,并将这些数据分成6组并作出样本的频率分布直方图,但不小心污损了部分图形(如图所示),则下列说法中正确的是( )
A.样本中分数落在的频数为45人 B.样本的众数为75分
C.样本的平均数为75分 D.样本的80百分位数为85分
三、填空题
13.口袋中装有100个大小相同的红球、白球和黑球,从中任意摸出一个,摸出红球或白球的概率为,摸出白球或黑球的概率为,那么口袋中共有白球、红球、黑球各 个.
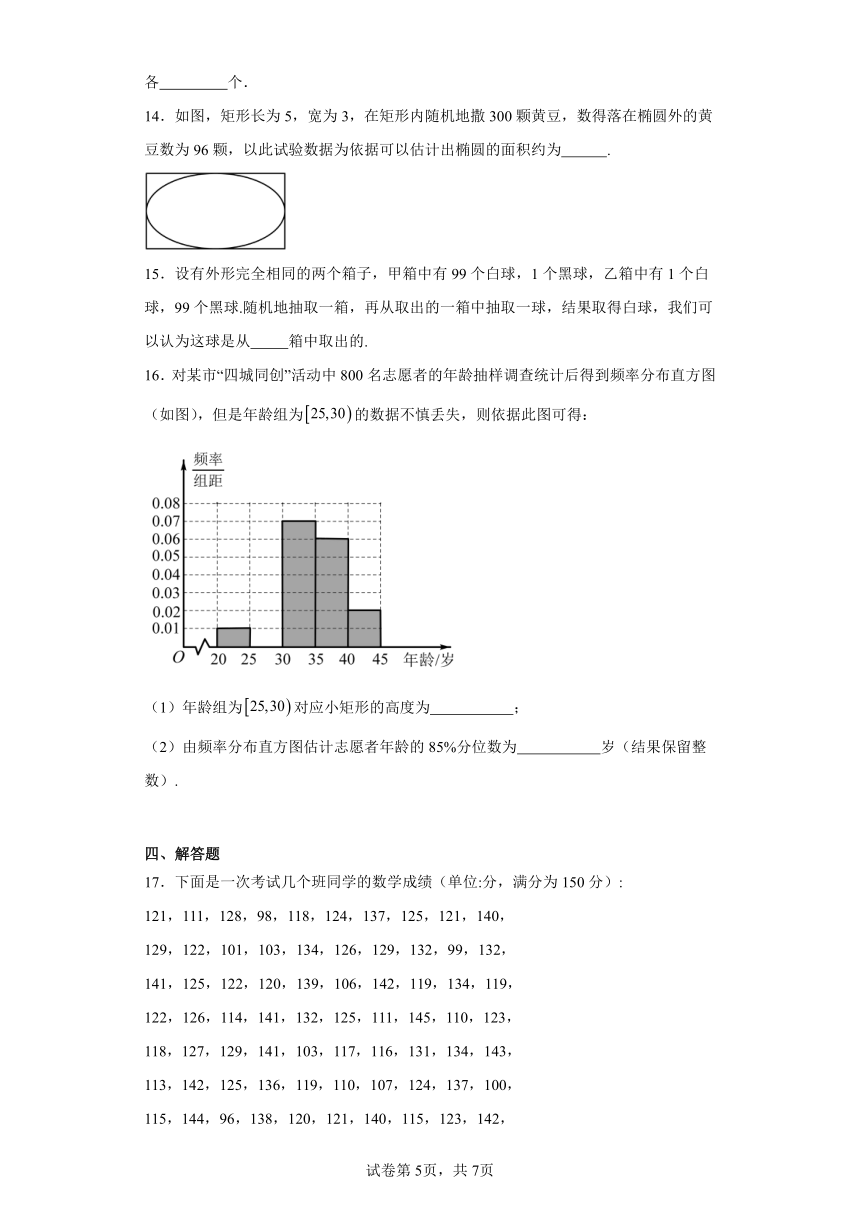
14.如图,矩形长为5,宽为3,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此试验数据为依据可以估计出椭圆的面积约为 .
15.设有外形完全相同的两个箱子,甲箱中有99个白球,1个黑球,乙箱中有1个白球,99个黑球.随机地抽取一箱,再从取出的一箱中抽取一球,结果取得白球,我们可以认为这球是从 箱中取出的.
16.对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为的数据不慎丢失,则依据此图可得:
(1)年龄组为对应小矩形的高度为 ;
(2)由频率分布直方图估计志愿者年龄的85%分位数为 岁(结果保留整数).
四、解答题
17.下面是一次考试几个班同学的数学成绩(单位:分,满分为150分):
121,111,128,98,118,124,137,125,121,140,
129,122,101,103,134,126,129,132,99,132,
141,125,122,120,139,106,142,119,134,119,
122,126,114,141,132,125,111,145,110,123,
118,127,129,141,103,117,116,131,134,143,
113,142,125,136,119,110,107,124,137,100,
115,144,96,138,120,121,140,115,123,142,
119,133,120,146,119,144,119,122,119,136,
137,132,112,133,134,117,127,133,126,127,
141,119,131,131,123,128,133,126,129,134,
127,133,121,135,107,132,121,137,118,117,
107,133,131,131,125,126,140,127,114,136,
118,138,127,143,81,140,135,137,142,136,
139,124,138,119,122,136,141,119,118,114.
(1)你觉得怎样直观地表示出上述数据的大致分布情况(比如哪个分数段的人数比较多,哪个分数段的人数比较少)
(2)画出频率分布直方图,看这次考试的整体分布,能说明哪些问题
18.人类的四种血型与基因类型的对应为:O型的基因类型为ii,A型的基因类型为ai或aa,B型的基因类型为bi或bb,AB型的基因类型为ab.其中a和b是显性基因,i是隐性基因.孩子分别继承父母一个基因,组成一个基因类型,则
(1)若一对夫妻的血型一个是A型,一个是AB型,分析他们子女的血型是O,A,B或AB型的概率;
(2)父母为哪种血型时,孩子的血型不可能为O型(写出结论即可)
19.某商超通过产品 价格 渠道和促销等各种营销策略,销售业绩得到不断提升,商超利润也有较大的攀升,经统计,该商超近7周的利润数据如下:
第周 1 2 3 4 5 6 7
商超利润(单位:万元) 32 35 36 45 47 51 55
(1)若关于具有较强的线性相关关系,求关于的线性回归方程,并预测该商超下周的利润;
(2)该商超为提升业绩,决定对客户开展抽奖促销活动:单张小票不超过500元可参加抽奖一次;单张小票超过500元可参加抽奖两次.若抽中“一等奖”,可获得30元的代金券;抽中“二等奖”,可获得20元的代金券;抽中“谢谢参与”,则没有奖励.已知本次抽奖活动中获得“一等奖”的概率为,获得二等奖”的概率为.某客户有两次参与抽奖活动的机会,假设两次抽奖之间是否中奖相互独立,求该客户所获得代金券总额(元)的分布列及数学期望.
附:;参考数据:
20.某种婴儿用品主要材质是橡胶,在加工过程中,可能会残留一些未挥发完全的溶剂,以及橡胶本身含有的化合物等,长期潜伏积累,对免疫力尚未健全的婴幼儿会危害甚大,为了测量此类新产品的挥发性物质含量,从生产的产品中随机抽取100个,得到如下频率分布直方图,若以频率作为概率,规定该婴儿用品的挥发性物质含量<18‰为合格产品.
(1)若这100个产品的挥发性物质含量的平均值大于16,则需进行技术改进,试问该新产品是否需要技术改进?
(2)为了解产品不合格的原因,用分层抽样的方法从与中抽取6个进行分析,然后从这6个中抽取2个进一步实验,求2个均在内的概率.
21.某初级中学正在开展“文明城市创建人人参与,志愿服务我当先行”的创文活动.为了了解该校志愿者参与服务的情况,现对该校全体志愿者进行随机抽样调查.根据调查数据绘制了不完整统计图(如图),条形统计图中七年级、八年级、九年级、教师分别指七年级、八年级、九年级、教师志愿者中被抽到的志愿者,扇形统计图中的百分数指的是该年级被抽到的志愿者人数与样本容量的百分比.
(1)请补全条形统计图.
(2)请你求出扇形统计图中教师所对应的扇形的圆心角的度数.
(3)若该校共有志愿者人,则该校七年级大约有多少名志愿者?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】先求出的长,再分别求出正六边形和正六边形的面积,再根据几何概型的面积比即可求得结论.
【详解】设正六边形的边长为1,在正六边形中,,
则易得,所以,
,
,
所以所求概率为.
故选:C.
2.D
【分析】先求出合格品的长度区间,从而可求解.
【详解】因为某产品的设计长度为,规定误差不超过为合格品,且,
所以长度在的为合格品,
所以这批产品的不合格率为.
故选:D.
3.D
【分析】数形结合,根据柱状图中给定数据结合题意代入所有选项求值即可得到D选项数据计算错误.
【详解】
选项 正误 原因
A √ 由条形图可知社会保险基金在2016~2019年收入是逐年递增的
B √ 社会保险基金在2016~2019年间收支并未出现“赤字”
C √ 2020年三项社会保险基金收入合计50666亿元,比上年减少8464亿元,约减少14.3%
D × 2020年三项社会保险基金支出合计57580亿元,比上年增加3088亿元,约增长5.7%,选项D是6.7%,故D错误
故选:D.
4.A
【分析】根据百分位数的定义判断求解.
【详解】因为,所以这组数据的第65百分位数是第6项数据4.5,
所以应有5个数不大于4.5,则,
故选:A.
5.B
【解析】根据概率的定义进行判断.
【详解】解:中奖概率表示每一次抽奖中奖的可能性都是,
故不论抽奖多少次,都可能一次也不中奖,
故选:B.
【点睛】此题考查对概率定义的理解,属于基础题
6.B
【分析】根据雷达图中所给的信息,逐项分析即可.
【详解】由六维能力雷达图,得:
对于A,甲的推理能力为比其他都低,故A正确;
对于B,甲的创造能力是,观察能力也是,故甲的创造力与于观察能力一样,故B误;
对于C,乙的计算能力是,甲的计算能力是,故乙的计算能力优于甲的计算能力,故C正确;
对于D,乙的六大能力总和为,甲的六大能力总和为,故D正确.
故选:B.
【点睛】本题考查命题真假的判断,考查读图识图能力、分析判断能力,是基础题.
7.C
【解析】根据近视率估计有多少人得了近视即可得解;
【详解】解:依题意,该市在校中学生的近视率约为78.7%.
故600人中大约有
故眼镜商应带滴眼液的瓶数应不少于473瓶
故选:
【点睛】本题考查概率的应用,属于基础题.
8.B
【分析】设共有个小孩,根据概率相等得出,可解出的值,从而得出小孩的人数.
【详解】设共有个小孩,由题意可得,解得,因此,估计一共有小孩人,
故选B.
【点睛】本题考查随机抽样和概率知识的应用,根据概率相等得出等式是解题的关键,考查运算求解能力,属于基础题.
9.BD
【分析】A项由占比和为可得“生活用品及服务”上人均消费支出的占比;B项由“生活用品及服务”上人均消费支出的占比与支出可得;CD项由支出占比大小比较可得.
【详解】选项A,,故A正确;
选项B,由题意,在“生活用品及服务”上人均消费支出的占比为6%,且支出为1281元,
则2019年居民人均消费支出为元,故B错误;
选项C,2019年居民在“教育文化娱乐”上人均消费支出占比,故C正确:
选项D,2019年居民在“教育文化娱乐”、“生活用品及服务”、“衣着”上的人均消费支出占比之和为,故D错误.
故选:BD.
10.AC
【分析】由图表中所给数据进行分析判断即可.
【详解】由图表可得,年5G用户规模年增长率最高,故A正确;
年5G用户规模年增长户数最多为(万人),故B错;
由图表可知,从年开始,年与年5G用户规模年增长率增加,从年开始到年5G用户规模年增长率逐年递减,故C正确;
由于后五年5G用户数增长不大,数据较稳定,故方差小于前5年数据方差,所以D错.
故选:AC.
【点睛】本题考查统计图表的运用,考查学生读图获取信息的能力,较简单.
11.AD
【解析】结合扇形图与条形图分析对比,对选项逐一分析判断.
【详解】由条形图可知,余额总数逐年上升,故A项正确;由城乡储蓄构成百分比可知,年农村居民存款年底总余额占,城镇居民存款年底总余额占,没有超过,故B项错误;城镇居民存款年底余额所占的比重逐年下降,但城镇居民存款年底余额年,年,年分别为(亿元),(亿元),(亿元),总体不是逐年下降的,故C项错误,年城乡居民存款年底余额增长率大约为,故D项正确.
故选:AD.
12.AB
【分析】根据频率分布直方图得到各组概率,根据概率和为1得到分数落在的频率进而求解其频数,从而判断A;根据频率最高的区间得到众数,从而判断B;根据频率分布直方图的平均数与百分位数求法计算,从而判断C和D.
【详解】设分数落在的频率为,
由题意得,各组频率依次为,,,,,,
所以,解得.
对于A,样本中分数落在的频数为人,故A正确;
对于B,由题意知,样本中的频率最高,所以众数为75分,故B正确;
对于C,样本的平均数为分,故C错误;
对于D,分数小于80的频率为,分数小于90的频率为,所以样本的80百分位数位于,设为,
则,解得,故D错误.
故选:AB
13.35,40,25
【分析】先根据概率计算对应颜色球的个数,结合总数100可得.
【详解】由题意,红球和白球的个数为,
白球和黑球的个数为,
所以白球个数为,
红球的个数为,
黑球的个数为,
故答案为:35,40,25
14./
【分析】利用概率模拟,利用图形的面积比等于黄豆数总数与落在椭圆内的黄豆数之比,从而得出答案.
【详解】因为矩形的面积为,设椭圆的面积为,
则,
解得.
故答案为:10.2.
15.甲.
【解析】分别求出甲箱中取到白球的概率和乙箱中取到白球的概率,由此进行判断.
【详解】解:甲箱有99个白球1个黑球,
随机地取出一球,得白球的可能性是,
乙箱中有1个白球和99个黑球,从中任取一球,得白球的可能性是,
由此看到,这一白球从甲箱中抽出的概率比从乙箱中抽出的概率大得多.
既然在一次抽样中抽得白球,当然可以认为是由概率大的箱子中抽出的.
我们作出推断是从甲箱中抽出的.
故答案为:甲
【点睛】本题考查概率的应用,属于基础题,解题时要认真审题,注意概率的计算.
16. 0.04/ 39
【分析】(1)根据频率分布直方图的特征及图中数据,列等式计算即可;
(2)根据分位数的定义及题中数据计算可得出结果.
【详解】(1)设所对应小矩形的高度为,根据题意,
,计算得, ;
(2)根据分位数的定义,设志愿者年龄的85%分位数为x,则
解得.
故答案为:0.04;39.
17.(1)答案见解析
(2)答案见解析
【分析】(1)数据比较多的时候,常借助频率分布表或频率分布直方图进行表示.
(2)利用频率分布表和频率分布直方图的特征即可得出结论.
【详解】(1)数据比较多的时候,要想获得数据的大致分布情况,
最好借助我们学过的图表,比如频率分布表、频率分布直方图.
(2)列频率分布表如下:
成绩分组(分) 频数 频率
合计
画频率分布直方图,如图所示:
通过频率分布直方图我们可以看到,
大部分同学的成绩集中在分数段内,
说明本次考试成绩难度不大,而个别同学成绩较低,
可能学习上遇到了困难,应该引起关注.
18.(1);;;;
(2)父母有一方是AB血型时,孩子的血型不可能为O型.
【分析】(1)列举所有基本事件,然后求出个事件包含的个数,利用古典概型概率公式求解即可;
(2)求出各个血型的概率,即可得出结论.
【详解】(1)若一对夫妻的血型一个是A型,一个是AB型,
则他们子女血型的基因的可能结果如下:aa,ab,ai,bi,aa,ab,aa,ab共8个,
O型的基因类型有0个,A型的基因类型有4个,B型的基因类型有1个,AB型的基因类型有3个,
故他们子女的血型是O的概率为,他们子女的血型是A的概率为,
他们子女的血型是B型的概率为,他们子女的血型是AB型的概率为;
(2)当父母的血型一个是A型,一个是AB型时,孩子的血型不可能为O型;
当父母的血型都是AB型时,子女血型的基因的可能结果如下:aa,ab,ab,bb共4个,
O型的基因类型有0个,故子女的血型是O的概率为,即孩子的血型不可能为O型;
当父母的血型一个是B型,一个是AB型时,则子女血型的基因的可能结果如下:ab,bb,ai,bi,ab,bb,ab,bb共8个,
O型的基因类型有0个,故子女的血型是O的概率为,即孩子的血型不可能为O型;
当父母的血型一个是O型,一个是AB型时,则子女血型的基因的可能结果如下:ai,ai,ai,bi共4个,O型的基因类型有0个,
故子女的血型是O的概率为,即孩子的血型不可能为O型;
综上,父母有一方是AB血型时,孩子的血型不可能为O型.
19.(1),59万元
(2)分布列答案见解析,数学期望:(元)
【分析】(1)根据已知条件,结合最小二乘法和线性回归方程的公式,即可得线性回归方程,再将点代入该线性回归方程即可求解.
(2)由题意可得,的所有可能取值为,分别求出对应的概率,即可得的分布列,从而求得数学期望.
【详解】(1)(1)根据表中数据,计算可得:
所以.
又因为,所以.
所以.
所以关于的线性回归方程为.
当时,得.
所以预测该商超下周的利润为59万元.
(2)(2)该客户所获得的代金券总额的所有可能取值有.
,
代金券总额的分布列如下表:
0 20 30 40 50 60
所以(元).
20.(1)该产品需要进行技术改进;(2).
【分析】(1)、由频率分布直方图求出平均值判断与16的大小关系即可得出结论;
(2)、先根据分层抽样求得在与中所抽取的个数,运用列举法列出事件的所有情况,由古典概率公式可求得答案.
【详解】(1)∵,故该产品需要进行技术改进;
(2)组的产品的个数为,组的产品的个数,所以从组中抽取个,从组中抽取个,
记组中抽取的5个分别为,组中抽取的一个为,
则从6个中抽取2个的所有情况如下:共15种情况,
其中在中恰有2个的有共10种情况,所以所求的概率.
21.(1)条形统计图见解析;(2);(3)名.
【分析】(1)本题首先可根据题意求出样本容量、八年级志愿者被抽到的人数以及九年级志愿者被抽到的人数,然后补全条形统计图即可;
(2)可根据教师志愿者被抽到的人数所占百分比求出对应的圆心角的度数;
(3)可通过总人数以及七年级志愿者所占比例得出结果.
【详解】(1)由题意知样本容量为,
则八年级志愿者被抽到的人数为,
九年级志愿者被抽到的人数为,
补全条形统计图如下:
(2)因为教师志愿者被抽到的人数所占百分比为,
所以对应的扇形的圆心角的度数为.
(3)(名),该校七年级大约有240名志愿者.
【点睛】本题考查条形统计图以及扇形统计图的实际应用,考查如何补全条形统计图,考查条形统计图以及扇形统计图之间的关系,考查计算能力,是简单题.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,正六边形的顶点是正六边形的对角线的交点.在正六边形内部任取一点,则该点取自正六边形内的概率为( )
A. B. C. D.
2.某产品的设计长度为,规定误差不超过为合格品.今对一批产品进行测量,测量结果如下表:
长度 以下 以上
件数 5 68 7
则这批产品的不合格率为( )
A. B. C. D.
3.“社保”已经走入了我们的生活,它包括养老保险、医疗保险、失业保险、工伤保险、生育保险.全年支出最重要的三项分别为养老保险、失业保险、工伤保险三项,下图是近五年三项社会保险基金的收支情况,下列说法中错误的是( )
A.三项社会保险基金在2020年以前收入为逐年递增
B.三项社会保险基金在2016~2019年间收支并未出现“赤字”
C.2020年三项社会保险基金收入合计50666亿元,比上年减少8464亿元,约减少14.3%
D.2020年三项社会保险基金支出合计57580亿元,比上年增加3088亿元,约增长6.7%
4.数据3.2,3.4,3.8,4.2,4.3,4.5,x,6.6的第65百分位数是4.5,则实数x的取值范围是( )
A. B. C. D.
5.在北京消费季活动中,某商场为促销举行购物抽奖活动,规定购物消费每满200元就可以参加一次抽奖活动,中奖的概率为.那么以下理解正确的是( )
A.某顾客抽奖10次,一定能中奖1次
B.某顾客抽奖10次,可能1次也没中奖
C.某顾客消费210元,一定不能中奖
D.某顾客消费1000元,至少能中奖1次
6.某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分,分值高者为优),分别绘制了如图所示的六维能力雷达图,图中点A表示甲的创造力指标值为4,点B表示乙的空间能力指标值为3,则下列叙述错误的是( )
A.甲的六大能力中推理能力最差 B.甲的创造力优于观察能力
C.乙的计算能力优于甲的计算能力 D.乙的六大能力整体水平低于甲
7.根据某市疾控中心的健康监测,该市在校中学生的近视率约为78.7%.某眼镜厂商要到中学给近视学生配送滴眼液,每人一瓶,已知该校学生总数为600人,则眼镜商应带滴眼液的瓶数为( )
A.600 B.787 C.不少于473 D.不多于473
8.从一群正在做游戏的小孩中抽出人,一人分一个苹果后,让他们返回继续游戏,一会儿,再从中任取人,发现其中有个小孩曾分过苹果,估计一共有小孩( )
A.人 B.人 C.人 D.人
二、多选题
9.2020年1月17日,国家统计局发布了2019年全国居民人均消费支出及其构成的情况,并绘制了如图的饼图.根据饼图判断,下列说法不正确的是( )
A.2019年居民在“生活用品及服务”上人均消费支出的占比为6%
B.2019年居民人均消费支出为23350元
C.2019年居民在“教育文化娱乐”上人均消费支出小于这8项人均消费支出的平均数
D.2019年居民在“教育文化娱乐”、“生活用品及服务”、“衣着”上的人均消费支出之和大于在“食品烟酒”上的人均消费支出
10.2020年两会“部长通道”工信部部长表示,中国每周大概增加1万多个5G基站,4月份增加5G用户700多万人,5G通信将成为社会发展的关键动力,下图是某机构对我国未来十年5G用户规模的发展预测图.则( )
A.2022年我国5G用户规模年增长率最高
B.2022年我国5G用户规模年增长户数最多
C.从2020年到2026年,我国的5G用户规模增长两年后,其年增长率逐年下降
D.这十年我国的5G用户数规模,后5年的平均数与方差都分别大于前5年的平均数与方差
11.某地区城乡居民储蓄存款年底余额(单位:亿元)变化情况如图所示,下列判断一定正确的是( )
A.该地区城乡居民储蓄存款年底余额总数逐年上升
B.到年农村居民存款年底总余额已超过了城镇居民存款年底总余额
C.城镇居民存款年底余额逐年下降
D.年城乡居民存款年底余额增长率大约为
12.某校在开展的“体育节”活动中,为了解学生对“体育节”的满意程度,组织学生给活动打分(分数为整数,满分100分),发现分数均在内,从中随机抽取一个容量为300的样本,并将这些数据分成6组并作出样本的频率分布直方图,但不小心污损了部分图形(如图所示),则下列说法中正确的是( )
A.样本中分数落在的频数为45人 B.样本的众数为75分
C.样本的平均数为75分 D.样本的80百分位数为85分
三、填空题
13.口袋中装有100个大小相同的红球、白球和黑球,从中任意摸出一个,摸出红球或白球的概率为,摸出白球或黑球的概率为,那么口袋中共有白球、红球、黑球各 个.
14.如图,矩形长为5,宽为3,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96颗,以此试验数据为依据可以估计出椭圆的面积约为 .
15.设有外形完全相同的两个箱子,甲箱中有99个白球,1个黑球,乙箱中有1个白球,99个黑球.随机地抽取一箱,再从取出的一箱中抽取一球,结果取得白球,我们可以认为这球是从 箱中取出的.
16.对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为的数据不慎丢失,则依据此图可得:
(1)年龄组为对应小矩形的高度为 ;
(2)由频率分布直方图估计志愿者年龄的85%分位数为 岁(结果保留整数).
四、解答题
17.下面是一次考试几个班同学的数学成绩(单位:分,满分为150分):
121,111,128,98,118,124,137,125,121,140,
129,122,101,103,134,126,129,132,99,132,
141,125,122,120,139,106,142,119,134,119,
122,126,114,141,132,125,111,145,110,123,
118,127,129,141,103,117,116,131,134,143,
113,142,125,136,119,110,107,124,137,100,
115,144,96,138,120,121,140,115,123,142,
119,133,120,146,119,144,119,122,119,136,
137,132,112,133,134,117,127,133,126,127,
141,119,131,131,123,128,133,126,129,134,
127,133,121,135,107,132,121,137,118,117,
107,133,131,131,125,126,140,127,114,136,
118,138,127,143,81,140,135,137,142,136,
139,124,138,119,122,136,141,119,118,114.
(1)你觉得怎样直观地表示出上述数据的大致分布情况(比如哪个分数段的人数比较多,哪个分数段的人数比较少)
(2)画出频率分布直方图,看这次考试的整体分布,能说明哪些问题
18.人类的四种血型与基因类型的对应为:O型的基因类型为ii,A型的基因类型为ai或aa,B型的基因类型为bi或bb,AB型的基因类型为ab.其中a和b是显性基因,i是隐性基因.孩子分别继承父母一个基因,组成一个基因类型,则
(1)若一对夫妻的血型一个是A型,一个是AB型,分析他们子女的血型是O,A,B或AB型的概率;
(2)父母为哪种血型时,孩子的血型不可能为O型(写出结论即可)
19.某商超通过产品 价格 渠道和促销等各种营销策略,销售业绩得到不断提升,商超利润也有较大的攀升,经统计,该商超近7周的利润数据如下:
第周 1 2 3 4 5 6 7
商超利润(单位:万元) 32 35 36 45 47 51 55
(1)若关于具有较强的线性相关关系,求关于的线性回归方程,并预测该商超下周的利润;
(2)该商超为提升业绩,决定对客户开展抽奖促销活动:单张小票不超过500元可参加抽奖一次;单张小票超过500元可参加抽奖两次.若抽中“一等奖”,可获得30元的代金券;抽中“二等奖”,可获得20元的代金券;抽中“谢谢参与”,则没有奖励.已知本次抽奖活动中获得“一等奖”的概率为,获得二等奖”的概率为.某客户有两次参与抽奖活动的机会,假设两次抽奖之间是否中奖相互独立,求该客户所获得代金券总额(元)的分布列及数学期望.
附:;参考数据:
20.某种婴儿用品主要材质是橡胶,在加工过程中,可能会残留一些未挥发完全的溶剂,以及橡胶本身含有的化合物等,长期潜伏积累,对免疫力尚未健全的婴幼儿会危害甚大,为了测量此类新产品的挥发性物质含量,从生产的产品中随机抽取100个,得到如下频率分布直方图,若以频率作为概率,规定该婴儿用品的挥发性物质含量<18‰为合格产品.
(1)若这100个产品的挥发性物质含量的平均值大于16,则需进行技术改进,试问该新产品是否需要技术改进?
(2)为了解产品不合格的原因,用分层抽样的方法从与中抽取6个进行分析,然后从这6个中抽取2个进一步实验,求2个均在内的概率.
21.某初级中学正在开展“文明城市创建人人参与,志愿服务我当先行”的创文活动.为了了解该校志愿者参与服务的情况,现对该校全体志愿者进行随机抽样调查.根据调查数据绘制了不完整统计图(如图),条形统计图中七年级、八年级、九年级、教师分别指七年级、八年级、九年级、教师志愿者中被抽到的志愿者,扇形统计图中的百分数指的是该年级被抽到的志愿者人数与样本容量的百分比.
(1)请补全条形统计图.
(2)请你求出扇形统计图中教师所对应的扇形的圆心角的度数.
(3)若该校共有志愿者人,则该校七年级大约有多少名志愿者?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】先求出的长,再分别求出正六边形和正六边形的面积,再根据几何概型的面积比即可求得结论.
【详解】设正六边形的边长为1,在正六边形中,,
则易得,所以,
,
,
所以所求概率为.
故选:C.
2.D
【分析】先求出合格品的长度区间,从而可求解.
【详解】因为某产品的设计长度为,规定误差不超过为合格品,且,
所以长度在的为合格品,
所以这批产品的不合格率为.
故选:D.
3.D
【分析】数形结合,根据柱状图中给定数据结合题意代入所有选项求值即可得到D选项数据计算错误.
【详解】
选项 正误 原因
A √ 由条形图可知社会保险基金在2016~2019年收入是逐年递增的
B √ 社会保险基金在2016~2019年间收支并未出现“赤字”
C √ 2020年三项社会保险基金收入合计50666亿元,比上年减少8464亿元,约减少14.3%
D × 2020年三项社会保险基金支出合计57580亿元,比上年增加3088亿元,约增长5.7%,选项D是6.7%,故D错误
故选:D.
4.A
【分析】根据百分位数的定义判断求解.
【详解】因为,所以这组数据的第65百分位数是第6项数据4.5,
所以应有5个数不大于4.5,则,
故选:A.
5.B
【解析】根据概率的定义进行判断.
【详解】解:中奖概率表示每一次抽奖中奖的可能性都是,
故不论抽奖多少次,都可能一次也不中奖,
故选:B.
【点睛】此题考查对概率定义的理解,属于基础题
6.B
【分析】根据雷达图中所给的信息,逐项分析即可.
【详解】由六维能力雷达图,得:
对于A,甲的推理能力为比其他都低,故A正确;
对于B,甲的创造能力是,观察能力也是,故甲的创造力与于观察能力一样,故B误;
对于C,乙的计算能力是,甲的计算能力是,故乙的计算能力优于甲的计算能力,故C正确;
对于D,乙的六大能力总和为,甲的六大能力总和为,故D正确.
故选:B.
【点睛】本题考查命题真假的判断,考查读图识图能力、分析判断能力,是基础题.
7.C
【解析】根据近视率估计有多少人得了近视即可得解;
【详解】解:依题意,该市在校中学生的近视率约为78.7%.
故600人中大约有
故眼镜商应带滴眼液的瓶数应不少于473瓶
故选:
【点睛】本题考查概率的应用,属于基础题.
8.B
【分析】设共有个小孩,根据概率相等得出,可解出的值,从而得出小孩的人数.
【详解】设共有个小孩,由题意可得,解得,因此,估计一共有小孩人,
故选B.
【点睛】本题考查随机抽样和概率知识的应用,根据概率相等得出等式是解题的关键,考查运算求解能力,属于基础题.
9.BD
【分析】A项由占比和为可得“生活用品及服务”上人均消费支出的占比;B项由“生活用品及服务”上人均消费支出的占比与支出可得;CD项由支出占比大小比较可得.
【详解】选项A,,故A正确;
选项B,由题意,在“生活用品及服务”上人均消费支出的占比为6%,且支出为1281元,
则2019年居民人均消费支出为元,故B错误;
选项C,2019年居民在“教育文化娱乐”上人均消费支出占比,故C正确:
选项D,2019年居民在“教育文化娱乐”、“生活用品及服务”、“衣着”上的人均消费支出占比之和为,故D错误.
故选:BD.
10.AC
【分析】由图表中所给数据进行分析判断即可.
【详解】由图表可得,年5G用户规模年增长率最高,故A正确;
年5G用户规模年增长户数最多为(万人),故B错;
由图表可知,从年开始,年与年5G用户规模年增长率增加,从年开始到年5G用户规模年增长率逐年递减,故C正确;
由于后五年5G用户数增长不大,数据较稳定,故方差小于前5年数据方差,所以D错.
故选:AC.
【点睛】本题考查统计图表的运用,考查学生读图获取信息的能力,较简单.
11.AD
【解析】结合扇形图与条形图分析对比,对选项逐一分析判断.
【详解】由条形图可知,余额总数逐年上升,故A项正确;由城乡储蓄构成百分比可知,年农村居民存款年底总余额占,城镇居民存款年底总余额占,没有超过,故B项错误;城镇居民存款年底余额所占的比重逐年下降,但城镇居民存款年底余额年,年,年分别为(亿元),(亿元),(亿元),总体不是逐年下降的,故C项错误,年城乡居民存款年底余额增长率大约为,故D项正确.
故选:AD.
12.AB
【分析】根据频率分布直方图得到各组概率,根据概率和为1得到分数落在的频率进而求解其频数,从而判断A;根据频率最高的区间得到众数,从而判断B;根据频率分布直方图的平均数与百分位数求法计算,从而判断C和D.
【详解】设分数落在的频率为,
由题意得,各组频率依次为,,,,,,
所以,解得.
对于A,样本中分数落在的频数为人,故A正确;
对于B,由题意知,样本中的频率最高,所以众数为75分,故B正确;
对于C,样本的平均数为分,故C错误;
对于D,分数小于80的频率为,分数小于90的频率为,所以样本的80百分位数位于,设为,
则,解得,故D错误.
故选:AB
13.35,40,25
【分析】先根据概率计算对应颜色球的个数,结合总数100可得.
【详解】由题意,红球和白球的个数为,
白球和黑球的个数为,
所以白球个数为,
红球的个数为,
黑球的个数为,
故答案为:35,40,25
14./
【分析】利用概率模拟,利用图形的面积比等于黄豆数总数与落在椭圆内的黄豆数之比,从而得出答案.
【详解】因为矩形的面积为,设椭圆的面积为,
则,
解得.
故答案为:10.2.
15.甲.
【解析】分别求出甲箱中取到白球的概率和乙箱中取到白球的概率,由此进行判断.
【详解】解:甲箱有99个白球1个黑球,
随机地取出一球,得白球的可能性是,
乙箱中有1个白球和99个黑球,从中任取一球,得白球的可能性是,
由此看到,这一白球从甲箱中抽出的概率比从乙箱中抽出的概率大得多.
既然在一次抽样中抽得白球,当然可以认为是由概率大的箱子中抽出的.
我们作出推断是从甲箱中抽出的.
故答案为:甲
【点睛】本题考查概率的应用,属于基础题,解题时要认真审题,注意概率的计算.
16. 0.04/ 39
【分析】(1)根据频率分布直方图的特征及图中数据,列等式计算即可;
(2)根据分位数的定义及题中数据计算可得出结果.
【详解】(1)设所对应小矩形的高度为,根据题意,
,计算得, ;
(2)根据分位数的定义,设志愿者年龄的85%分位数为x,则
解得.
故答案为:0.04;39.
17.(1)答案见解析
(2)答案见解析
【分析】(1)数据比较多的时候,常借助频率分布表或频率分布直方图进行表示.
(2)利用频率分布表和频率分布直方图的特征即可得出结论.
【详解】(1)数据比较多的时候,要想获得数据的大致分布情况,
最好借助我们学过的图表,比如频率分布表、频率分布直方图.
(2)列频率分布表如下:
成绩分组(分) 频数 频率
合计
画频率分布直方图,如图所示:
通过频率分布直方图我们可以看到,
大部分同学的成绩集中在分数段内,
说明本次考试成绩难度不大,而个别同学成绩较低,
可能学习上遇到了困难,应该引起关注.
18.(1);;;;
(2)父母有一方是AB血型时,孩子的血型不可能为O型.
【分析】(1)列举所有基本事件,然后求出个事件包含的个数,利用古典概型概率公式求解即可;
(2)求出各个血型的概率,即可得出结论.
【详解】(1)若一对夫妻的血型一个是A型,一个是AB型,
则他们子女血型的基因的可能结果如下:aa,ab,ai,bi,aa,ab,aa,ab共8个,
O型的基因类型有0个,A型的基因类型有4个,B型的基因类型有1个,AB型的基因类型有3个,
故他们子女的血型是O的概率为,他们子女的血型是A的概率为,
他们子女的血型是B型的概率为,他们子女的血型是AB型的概率为;
(2)当父母的血型一个是A型,一个是AB型时,孩子的血型不可能为O型;
当父母的血型都是AB型时,子女血型的基因的可能结果如下:aa,ab,ab,bb共4个,
O型的基因类型有0个,故子女的血型是O的概率为,即孩子的血型不可能为O型;
当父母的血型一个是B型,一个是AB型时,则子女血型的基因的可能结果如下:ab,bb,ai,bi,ab,bb,ab,bb共8个,
O型的基因类型有0个,故子女的血型是O的概率为,即孩子的血型不可能为O型;
当父母的血型一个是O型,一个是AB型时,则子女血型的基因的可能结果如下:ai,ai,ai,bi共4个,O型的基因类型有0个,
故子女的血型是O的概率为,即孩子的血型不可能为O型;
综上,父母有一方是AB血型时,孩子的血型不可能为O型.
19.(1),59万元
(2)分布列答案见解析,数学期望:(元)
【分析】(1)根据已知条件,结合最小二乘法和线性回归方程的公式,即可得线性回归方程,再将点代入该线性回归方程即可求解.
(2)由题意可得,的所有可能取值为,分别求出对应的概率,即可得的分布列,从而求得数学期望.
【详解】(1)(1)根据表中数据,计算可得:
所以.
又因为,所以.
所以.
所以关于的线性回归方程为.
当时,得.
所以预测该商超下周的利润为59万元.
(2)(2)该客户所获得的代金券总额的所有可能取值有.
,
代金券总额的分布列如下表:
0 20 30 40 50 60
所以(元).
20.(1)该产品需要进行技术改进;(2).
【分析】(1)、由频率分布直方图求出平均值判断与16的大小关系即可得出结论;
(2)、先根据分层抽样求得在与中所抽取的个数,运用列举法列出事件的所有情况,由古典概率公式可求得答案.
【详解】(1)∵,故该产品需要进行技术改进;
(2)组的产品的个数为,组的产品的个数,所以从组中抽取个,从组中抽取个,
记组中抽取的5个分别为,组中抽取的一个为,
则从6个中抽取2个的所有情况如下:共15种情况,
其中在中恰有2个的有共10种情况,所以所求的概率.
21.(1)条形统计图见解析;(2);(3)名.
【分析】(1)本题首先可根据题意求出样本容量、八年级志愿者被抽到的人数以及九年级志愿者被抽到的人数,然后补全条形统计图即可;
(2)可根据教师志愿者被抽到的人数所占百分比求出对应的圆心角的度数;
(3)可通过总人数以及七年级志愿者所占比例得出结果.
【详解】(1)由题意知样本容量为,
则八年级志愿者被抽到的人数为,
九年级志愿者被抽到的人数为,
补全条形统计图如下:
(2)因为教师志愿者被抽到的人数所占百分比为,
所以对应的扇形的圆心角的度数为.
(3)(名),该校七年级大约有240名志愿者.
【点睛】本题考查条形统计图以及扇形统计图的实际应用,考查如何补全条形统计图,考查条形统计图以及扇形统计图之间的关系,考查计算能力,是简单题.
答案第1页,共2页
答案第1页,共2页
