福建省莆田市城厢区莆田擢英中学2023-2024学年九年级下学期开学数学试题(含答案)
文档属性
| 名称 | 福建省莆田市城厢区莆田擢英中学2023-2024学年九年级下学期开学数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 00:00:00 | ||
图片预览




文档简介
2023-2024学年擢英九年级(下)初中数学检查试卷
选择题(每小题只有一个正确的选项,本大题共10小题,每小题4分,共40分.)
1.下列各个数中属于无理数的是( )
A. 0.2 B. C. -1 D.
2.在下列四款国产汽车的车标图案中,是中心对称图形的是( )
A. B. C. D.
3.月日是中国航天日,年的这一天,我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射,标志着中国从此进入了太空时代,它的运行轨道距地球最近点米.将用科学记数法表示应为( )
A. B. C. D.439×
4.右图是我们生活中常用的“空心卷纸”,其主视图为( )
A. B. C. D.
5.下列计算结果正确的是( )
A. B. C.2α ·3α =6 D.
6.如图,已知a//b,一块含30°角的直角三角板,如图所示放置,∠2=30°,则∠1等于( )
A.110° B.130° C.150° D.160°
7.元朝朱世杰所著的《算学启蒙》中,记载了这样一道题:良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?其大意是:快马每天行里,慢马每天行160里,慢马先行天,快马几天可追上慢马?若设快马天可追上慢马,由题意得( )
A. = B.= -12 C.240(-12)=160 D.240=160(+12)
白老师在黑板上计算一组数据时,列式如下:,由公式提供的信息,下列关于这组数据的说法错误的是( )
A.中位数是4 B.众数是4 C.平均数是4 D.方差是
9.如图,PQ、PB、QC是⊙O的切线,切点分别为A、B、C,点D在上,若∠D=100°,则∠P与∠Q的度数之和是( )
A.160° B.140° C.120° D.100°
10.已知关于x的二次函数的与x轴的交点坐标是和,其中a,b,c,d均为常数,则关于x的二次函数与x轴的交点坐标是( )
A.和 B.和 C.和 D.和
二、填空题(本大题共6小题,每空4分,共24分.)
11.因式分解:-=
12.夹文件的一种燕尾夹如图1所示,图2是在闭合状态下的示意图,经测量知,,,则在闭合状态下,点B,D之间的距离是 .
图1 图2
13.如果圆锥底面圆的半径为,它的侧面积为24πcm ,那么它的母线长为 .
14.若α,β是方程x +2x-2026=0的两个实数根,则α +3α+β的值为
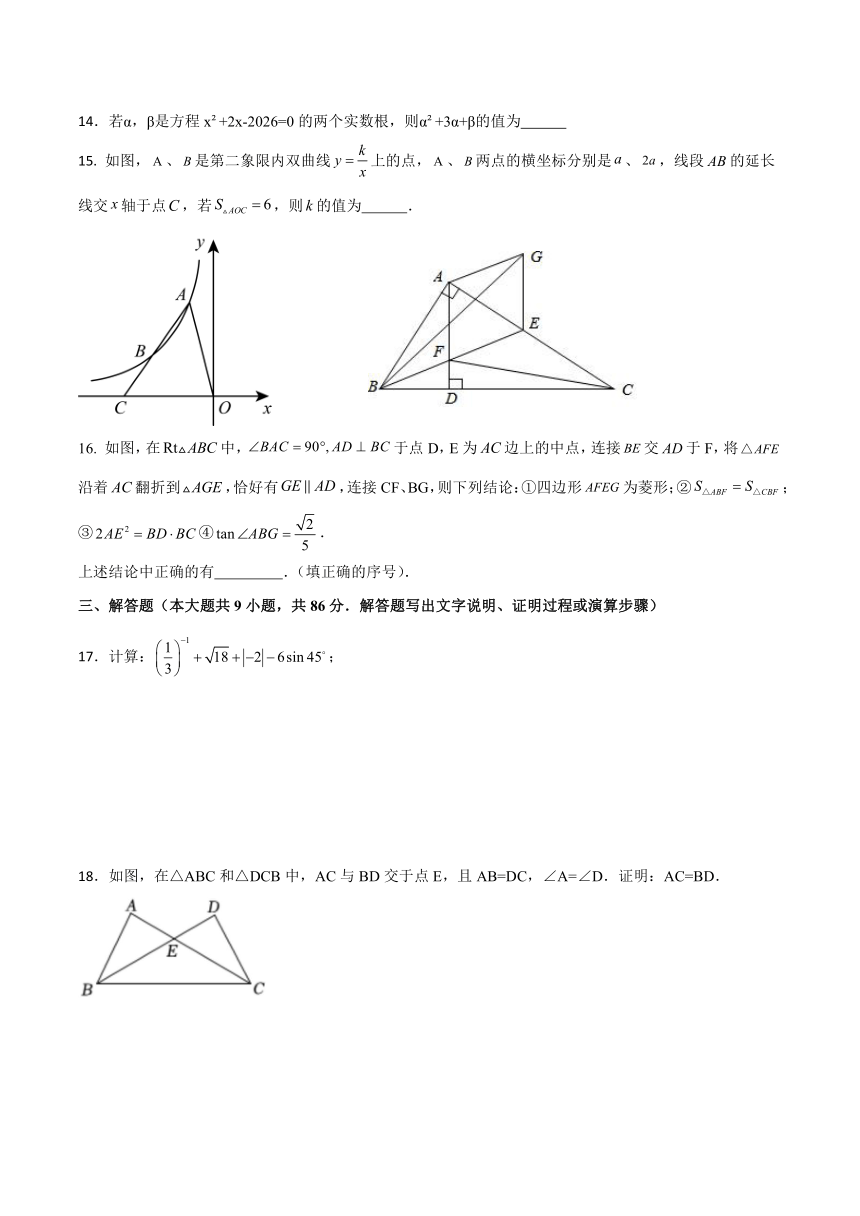
15. 如图,、是第二象限内双曲线上的点,、两点的横坐标分别是、,线段的延长线交轴于点,若,则的值为 .
如图,在中,于点D,E为边上的中点,连接交于F,将沿着翻折到,恰好有,连接CF、BG,则下列结论:①四边形为菱形;②;③④.
上述结论中正确的有 .(填正确的序号).
三、解答题(本大题共9小题,共86分.解答题写出文字说明、证明过程或演算步骤)
17.计算:;
18.如图,在△ABC和△DCB中,AC与BD交于点E,且AB=DC,∠A=∠D.证明:AC=BD.
19.先化简,再求值:(1 -)÷,其中a=-1.
20.为贯彻落实党的二十大精神,全面建设社会主义现代化国家、全面推进中华民族伟大复兴,某校团委举办以“无悔青春献祖国,接力奋斗新时代”为主题的征文比赛,每班限一人参赛,九年级(2)班的小莆和小田两人文采相当,且都想代表班级参赛,于是班长制作了5张正面分别写有,,0,1,2的卡片(卡片背面完全相同),将卡片背面朝上洗匀后,小莆先从中任意抽取一张,不放回,小田再从剩下的4张卡片中任意抽取一张,若两人所抽取的卡片上的数字之积为0,则小莆代表班级参赛;否则,小田代表班级参赛.
(1)小莆抽取的卡片正面上的数字是0的概率为________;
(2)请用列表法或画树状图的方法,判断班长设计的这个游戏规则对双方是否公平.
21.如图,在中,,是的平分线,且交于点.
(1)在斜边上求作点,使;(要求:尺规作图,不写作法,保留作图痕迹)
(2)若,,求的长.
22.某景区纪念品超市以50元每个的价格新进一批工艺摆件,经过一段时间的销售发现日销量(个)与单个售价(元)之间的函数关系如下图.(景区规定任何商品的利润率不得高于)
(1)根据图象,直接写出与的函数关系式;
(2)该超市要想每天获得2400元的销售利润,销售单价应定为多少元?
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
23.根据以下素材,探索完成任务.
探究遮阳伞下的影子长度
素材1 图1是某款自动旋转遮阳伞,伞面完全张开时张角呈,图2是其侧面示意图.已知支架AB长为2.5米,且垂直于地面BC,悬托架米,点E固定在伞面上,且伞面直径DF是DE的4倍.当伞面完全张开时,点D,E,F始终共线.为实现遮阳效果最佳,伞面装有接收器可以根据太阳光线的角度变化,自动调整手柄D沿着AB移动,以保证太阳光线与DF始终垂直.
素材2 某地区某天下午不同时间的太阳高度角(太阳光线与地面的夹角)参照表: 时刻12点13点14点15点16点17点太阳高度(度)907560453015参考数据:,.
素材3 小明坐在露营椅上的高度(头顶到地面的距离)约为1米.如图2,小明坐的位置记为点Q.
问题解决
任务1 确定影子长度 某一时刻测得米,请求出此时影子的长度.
任务2 判断是否照射到 这天14点,小明坐在离支架3米处的Q点,请判断此时小明是否会被太阳光照射到?
任务3 探究合理范围 小明打算在这天14:00-15:00露营休息,为保证小明全程不被太阳光照射到,请计算的取值范围.
24.如图1,抛物线y=-x +bx + c交x轴于A(-1,0)、B(3,0),交y轴于C,P是第一象限内抛物线上的一个动点.
(1)求抛物线的表达式;
(2)连接BC、AP,相交于点D,令z = ,当z的值最大时,求点P的坐标;
(3)如图2,抛物线的对称轴与x轴交于点E,直线AP、BP分别与对称轴交于点M、N,
△AME与△BNE的面积分别为、.设点P的横坐标为t,当125.如图,△ABC内接于⊙0,BC是⊙0的直径,tan∠ACB=2,过点A作AD⊥BC,交⊙0于点E,点F是弧AB上一点,连结EF交BC于点G,连结CF交AD于点H.
(1)求证: △AFC∽△HFE;
(2)若BC =10,CF=8,求EF的长
(3)设 =x, = y,求y关于x的函数表达式.
2023-2024学年擢英九年级(下)初中数学检查试卷 参考答案及解析
选择题(共10小题)
1-5:DBCCD 6-10:CDDAA
10.【详解】解:∵二次函数的与x轴的交点坐标是和,
∴方程的两个根分别为c、d,
∴,,
∴
∵,
设方程的两根为,,
∴,,
∴,分别为a、b,
∴该函数与x轴的交点坐标和,
故选:A.
填空题(共6小题)
11 .(x+2y)(x-2y) 12 .48 13 .6 14 .2024 15 .-4 16 .①②③
【详解】解:①∵将沿AC翻折到
∴四边形是菱形.
故①正确.
②
又
又
∵E是AC的中点,
故②正确.
③
故③正确.
④如图所示:过点G作交BA延长线于H,
设则
∵四边形是菱形,
故④错误.
故答案为:①②③.
解答题(共9小题)
17.5
18 .【详解】证明:∵∠A=∠D,
∴在△ABC和△DCB中,
,
∴△ABC≌△DCB,
∴AC=BD.
19 .【详解】原式=
当a=-1时,
原式=
20 .【详解】(1)解:∵一共有5张卡片,每张卡片被抽到的概率相同,
∴王伟抽取的卡片正面上的数字是0的概率为,
故答案为:;
(2)解:班长设计的这个游戏规则对双方不公平,理由如下:
列表如下:
0 1 2
(,) (0,) (1,) (2,)
(,) (0,) (1,) (2,)
0 (,) (,0) (1,0) (2,0)
1 (,1) (,1) (0,1) (2,1)
2 (,2) (,2) (0,2) (1,2)
由表格可知一共有20种等可能性的结果数,其中数字之积为0的结果数有8种,数字之积不为0的结果数有12种,
∴王伟参赛的概率为,孙莉参赛的概率为
∴班长设计的这个游戏规则对双方不公平.
21 .【详解】(1)解:如图,点即为所求;
(2),
,
,
,
平分,
,
,
,
∴,
∴,
∴.
22 .【详解】解:(1)设(,为常数)将点,代入得,
解得
∴y与x的函数关系式为:y= 2x+260;
(2)由题意得:,化简得:,
解得:,,
∵,且,
∴(舍去),
答:销售单价应定为70元.
(3)设每天获得的利润为元,由题意得,
∵,抛物线开口向下,
∴有最大值,当时,,
答:销售单价为90元时,每天获得的利润最大,最大利润是3200元.
23 .【详解】解(1)如图1,过点E作于点I,过点G作于点J.
∵,,
∴,
∵,
∴,
∴.
∵,
∴,
∴,
∵,四边形为矩形,
∴,,
∴,
∴,
在中,(米).
(2)方法1:
如图2,过点Q作交于点P.
由(1)知,,
在中,,
∴,
∴.
在中,,
在中,,
∵在中,当时,,
∴小明刚好被照射到时离B点的距离为,
∴小明会被照射到.
方法2:
如图2,过点Q作交FH于点P.
与方法1同理得,得,,
∴
在中,.
∴小明会被照射到.
(3)当时,.
当时,.
∴.
24 .【详解】解:(1)把A(1,0),B(3,0)代入y = -x +bx + c
得
解得
∴抛物线表达式为y = -x +2x + 3
把x=0代入表达式得y=3
∴点C的坐标为(0,3),
设直线BC的解析式为y=kx+b,代入B(3,0),C(0,3)
得
解得
∴直线BC的解析式为y = -x+3
设p(a,-a +2a+3),过点P作PQ∥x轴,交直线BC于点Q,
则Q坐标为(a -2a,-a +2a+3),
得PQ=-a +3a
∵PQ∥x轴,
∴△PDQ∽△ADB
∴z=-a +a(0<a<3)
当a=时,z取得最大值,此时点P的坐标为(,)
+的值不变,理由如下:
由抛物线可知对称轴为直线x=1,
由题得P(t,-t +2t+3),
设直线AP的解析式为y=x+,代入点A,点P
求得直线AP解析式为y=(-t+3)x-t+3,
把x=1代入解析式得:y=-2t+6
∴M(1,-2t+6)
∴ME=-2t+6
同理得BN的解析式为y=(-t-1)x+3t+3
N的坐标为(1,2t+2),
∴NE=2t+2
∴+ = AE·ME+BE·NE=ME+NE=8
25 .【详解】解:
证明:(1)证明:∵BC是⊙O的直径,AD⊥BC
∴∠AFC =∠CFE
∵∠ACF =∠FEA
∴△AFC∽△HFE:
(2)
连接BF
∵BC是⊙O的直径
∴∠BAC =90°,
tan ∠ACB =2,
∴AB=2AC
在Rt△ABC中,BC =10,
∴AC =2
∵AD⊥BC,
∴∠ADC =90°,
∵tan∠ACB =2
∴AD =2CD
在Rt△ACD中,
AD +CD =AC ,则
CD=2,AD =4,
∴ED = AD =4,
∵BC是⊙O的直径
∴∠BFC =90°,
∵BC =10,CF=8,
∴BF=6,
∵∠BFC =∠HDC =90°,
∠FCB =∠DCH,
∴△BFC∽△HDC
∴=
∴HD=
∴HE=ED+HD=
∵△AFC∽△HFE,
∴=
∴EF=
(3)设OC =r,则BC =2r,
∵tan∠ACB =2,.
∴AD =2CD,BD =2AD
∴CD=r ,AD=r,
①当点G在线段OD上时,
∵=x,
∴OG=xr, CG=(1-x)r, BG=(1+x)r,
过点G作GM⊥CF交于点M,
∴∠GMF=90°,
∵∠ADC=90°,∠CAE=∠CFE,
∴∠FCM=∠ACB
∴tan ∠FGM = tan ∠ACB =2,
∴FM =2GM,
∵∠GMC =∠BFC =90°,
∴GM∥BE,
∴=
∴=
∵=
∴=
∴DH=,
∴AH=AD-HD=r
∴=
∴y=
②当点G在线段OB上时,同理可得y=
综上所述:当点G在线段OD上时,y=
当点G在线段OB上时,y=
选择题(每小题只有一个正确的选项,本大题共10小题,每小题4分,共40分.)
1.下列各个数中属于无理数的是( )
A. 0.2 B. C. -1 D.
2.在下列四款国产汽车的车标图案中,是中心对称图形的是( )
A. B. C. D.
3.月日是中国航天日,年的这一天,我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射,标志着中国从此进入了太空时代,它的运行轨道距地球最近点米.将用科学记数法表示应为( )
A. B. C. D.439×
4.右图是我们生活中常用的“空心卷纸”,其主视图为( )
A. B. C. D.
5.下列计算结果正确的是( )
A. B. C.2α ·3α =6 D.
6.如图,已知a//b,一块含30°角的直角三角板,如图所示放置,∠2=30°,则∠1等于( )
A.110° B.130° C.150° D.160°
7.元朝朱世杰所著的《算学启蒙》中,记载了这样一道题:良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?其大意是:快马每天行里,慢马每天行160里,慢马先行天,快马几天可追上慢马?若设快马天可追上慢马,由题意得( )
A. = B.= -12 C.240(-12)=160 D.240=160(+12)
白老师在黑板上计算一组数据时,列式如下:,由公式提供的信息,下列关于这组数据的说法错误的是( )
A.中位数是4 B.众数是4 C.平均数是4 D.方差是
9.如图,PQ、PB、QC是⊙O的切线,切点分别为A、B、C,点D在上,若∠D=100°,则∠P与∠Q的度数之和是( )
A.160° B.140° C.120° D.100°
10.已知关于x的二次函数的与x轴的交点坐标是和,其中a,b,c,d均为常数,则关于x的二次函数与x轴的交点坐标是( )
A.和 B.和 C.和 D.和
二、填空题(本大题共6小题,每空4分,共24分.)
11.因式分解:-=
12.夹文件的一种燕尾夹如图1所示,图2是在闭合状态下的示意图,经测量知,,,则在闭合状态下,点B,D之间的距离是 .
图1 图2
13.如果圆锥底面圆的半径为,它的侧面积为24πcm ,那么它的母线长为 .
14.若α,β是方程x +2x-2026=0的两个实数根,则α +3α+β的值为
15. 如图,、是第二象限内双曲线上的点,、两点的横坐标分别是、,线段的延长线交轴于点,若,则的值为 .
如图,在中,于点D,E为边上的中点,连接交于F,将沿着翻折到,恰好有,连接CF、BG,则下列结论:①四边形为菱形;②;③④.
上述结论中正确的有 .(填正确的序号).
三、解答题(本大题共9小题,共86分.解答题写出文字说明、证明过程或演算步骤)
17.计算:;
18.如图,在△ABC和△DCB中,AC与BD交于点E,且AB=DC,∠A=∠D.证明:AC=BD.
19.先化简,再求值:(1 -)÷,其中a=-1.
20.为贯彻落实党的二十大精神,全面建设社会主义现代化国家、全面推进中华民族伟大复兴,某校团委举办以“无悔青春献祖国,接力奋斗新时代”为主题的征文比赛,每班限一人参赛,九年级(2)班的小莆和小田两人文采相当,且都想代表班级参赛,于是班长制作了5张正面分别写有,,0,1,2的卡片(卡片背面完全相同),将卡片背面朝上洗匀后,小莆先从中任意抽取一张,不放回,小田再从剩下的4张卡片中任意抽取一张,若两人所抽取的卡片上的数字之积为0,则小莆代表班级参赛;否则,小田代表班级参赛.
(1)小莆抽取的卡片正面上的数字是0的概率为________;
(2)请用列表法或画树状图的方法,判断班长设计的这个游戏规则对双方是否公平.
21.如图,在中,,是的平分线,且交于点.
(1)在斜边上求作点,使;(要求:尺规作图,不写作法,保留作图痕迹)
(2)若,,求的长.
22.某景区纪念品超市以50元每个的价格新进一批工艺摆件,经过一段时间的销售发现日销量(个)与单个售价(元)之间的函数关系如下图.(景区规定任何商品的利润率不得高于)
(1)根据图象,直接写出与的函数关系式;
(2)该超市要想每天获得2400元的销售利润,销售单价应定为多少元?
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
23.根据以下素材,探索完成任务.
探究遮阳伞下的影子长度
素材1 图1是某款自动旋转遮阳伞,伞面完全张开时张角呈,图2是其侧面示意图.已知支架AB长为2.5米,且垂直于地面BC,悬托架米,点E固定在伞面上,且伞面直径DF是DE的4倍.当伞面完全张开时,点D,E,F始终共线.为实现遮阳效果最佳,伞面装有接收器可以根据太阳光线的角度变化,自动调整手柄D沿着AB移动,以保证太阳光线与DF始终垂直.
素材2 某地区某天下午不同时间的太阳高度角(太阳光线与地面的夹角)参照表: 时刻12点13点14点15点16点17点太阳高度(度)907560453015参考数据:,.
素材3 小明坐在露营椅上的高度(头顶到地面的距离)约为1米.如图2,小明坐的位置记为点Q.
问题解决
任务1 确定影子长度 某一时刻测得米,请求出此时影子的长度.
任务2 判断是否照射到 这天14点,小明坐在离支架3米处的Q点,请判断此时小明是否会被太阳光照射到?
任务3 探究合理范围 小明打算在这天14:00-15:00露营休息,为保证小明全程不被太阳光照射到,请计算的取值范围.
24.如图1,抛物线y=-x +bx + c交x轴于A(-1,0)、B(3,0),交y轴于C,P是第一象限内抛物线上的一个动点.
(1)求抛物线的表达式;
(2)连接BC、AP,相交于点D,令z = ,当z的值最大时,求点P的坐标;
(3)如图2,抛物线的对称轴与x轴交于点E,直线AP、BP分别与对称轴交于点M、N,
△AME与△BNE的面积分别为、.设点P的横坐标为t,当1
(1)求证: △AFC∽△HFE;
(2)若BC =10,CF=8,求EF的长
(3)设 =x, = y,求y关于x的函数表达式.
2023-2024学年擢英九年级(下)初中数学检查试卷 参考答案及解析
选择题(共10小题)
1-5:DBCCD 6-10:CDDAA
10.【详解】解:∵二次函数的与x轴的交点坐标是和,
∴方程的两个根分别为c、d,
∴,,
∴
∵,
设方程的两根为,,
∴,,
∴,分别为a、b,
∴该函数与x轴的交点坐标和,
故选:A.
填空题(共6小题)
11 .(x+2y)(x-2y) 12 .48 13 .6 14 .2024 15 .-4 16 .①②③
【详解】解:①∵将沿AC翻折到
∴四边形是菱形.
故①正确.
②
又
又
∵E是AC的中点,
故②正确.
③
故③正确.
④如图所示:过点G作交BA延长线于H,
设则
∵四边形是菱形,
故④错误.
故答案为:①②③.
解答题(共9小题)
17.5
18 .【详解】证明:∵∠A=∠D,
∴在△ABC和△DCB中,
,
∴△ABC≌△DCB,
∴AC=BD.
19 .【详解】原式=
当a=-1时,
原式=
20 .【详解】(1)解:∵一共有5张卡片,每张卡片被抽到的概率相同,
∴王伟抽取的卡片正面上的数字是0的概率为,
故答案为:;
(2)解:班长设计的这个游戏规则对双方不公平,理由如下:
列表如下:
0 1 2
(,) (0,) (1,) (2,)
(,) (0,) (1,) (2,)
0 (,) (,0) (1,0) (2,0)
1 (,1) (,1) (0,1) (2,1)
2 (,2) (,2) (0,2) (1,2)
由表格可知一共有20种等可能性的结果数,其中数字之积为0的结果数有8种,数字之积不为0的结果数有12种,
∴王伟参赛的概率为,孙莉参赛的概率为
∴班长设计的这个游戏规则对双方不公平.
21 .【详解】(1)解:如图,点即为所求;
(2),
,
,
,
平分,
,
,
,
∴,
∴,
∴.
22 .【详解】解:(1)设(,为常数)将点,代入得,
解得
∴y与x的函数关系式为:y= 2x+260;
(2)由题意得:,化简得:,
解得:,,
∵,且,
∴(舍去),
答:销售单价应定为70元.
(3)设每天获得的利润为元,由题意得,
∵,抛物线开口向下,
∴有最大值,当时,,
答:销售单价为90元时,每天获得的利润最大,最大利润是3200元.
23 .【详解】解(1)如图1,过点E作于点I,过点G作于点J.
∵,,
∴,
∵,
∴,
∴.
∵,
∴,
∴,
∵,四边形为矩形,
∴,,
∴,
∴,
在中,(米).
(2)方法1:
如图2,过点Q作交于点P.
由(1)知,,
在中,,
∴,
∴.
在中,,
在中,,
∵在中,当时,,
∴小明刚好被照射到时离B点的距离为,
∴小明会被照射到.
方法2:
如图2,过点Q作交FH于点P.
与方法1同理得,得,,
∴
在中,.
∴小明会被照射到.
(3)当时,.
当时,.
∴.
24 .【详解】解:(1)把A(1,0),B(3,0)代入y = -x +bx + c
得
解得
∴抛物线表达式为y = -x +2x + 3
把x=0代入表达式得y=3
∴点C的坐标为(0,3),
设直线BC的解析式为y=kx+b,代入B(3,0),C(0,3)
得
解得
∴直线BC的解析式为y = -x+3
设p(a,-a +2a+3),过点P作PQ∥x轴,交直线BC于点Q,
则Q坐标为(a -2a,-a +2a+3),
得PQ=-a +3a
∵PQ∥x轴,
∴△PDQ∽△ADB
∴z=-a +a(0<a<3)
当a=时,z取得最大值,此时点P的坐标为(,)
+的值不变,理由如下:
由抛物线可知对称轴为直线x=1,
由题得P(t,-t +2t+3),
设直线AP的解析式为y=x+,代入点A,点P
求得直线AP解析式为y=(-t+3)x-t+3,
把x=1代入解析式得:y=-2t+6
∴M(1,-2t+6)
∴ME=-2t+6
同理得BN的解析式为y=(-t-1)x+3t+3
N的坐标为(1,2t+2),
∴NE=2t+2
∴+ = AE·ME+BE·NE=ME+NE=8
25 .【详解】解:
证明:(1)证明:∵BC是⊙O的直径,AD⊥BC
∴∠AFC =∠CFE
∵∠ACF =∠FEA
∴△AFC∽△HFE:
(2)
连接BF
∵BC是⊙O的直径
∴∠BAC =90°,
tan ∠ACB =2,
∴AB=2AC
在Rt△ABC中,BC =10,
∴AC =2
∵AD⊥BC,
∴∠ADC =90°,
∵tan∠ACB =2
∴AD =2CD
在Rt△ACD中,
AD +CD =AC ,则
CD=2,AD =4,
∴ED = AD =4,
∵BC是⊙O的直径
∴∠BFC =90°,
∵BC =10,CF=8,
∴BF=6,
∵∠BFC =∠HDC =90°,
∠FCB =∠DCH,
∴△BFC∽△HDC
∴=
∴HD=
∴HE=ED+HD=
∵△AFC∽△HFE,
∴=
∴EF=
(3)设OC =r,则BC =2r,
∵tan∠ACB =2,.
∴AD =2CD,BD =2AD
∴CD=r ,AD=r,
①当点G在线段OD上时,
∵=x,
∴OG=xr, CG=(1-x)r, BG=(1+x)r,
过点G作GM⊥CF交于点M,
∴∠GMF=90°,
∵∠ADC=90°,∠CAE=∠CFE,
∴∠FCM=∠ACB
∴tan ∠FGM = tan ∠ACB =2,
∴FM =2GM,
∵∠GMC =∠BFC =90°,
∴GM∥BE,
∴=
∴=
∵=
∴=
∴DH=,
∴AH=AD-HD=r
∴=
∴y=
②当点G在线段OB上时,同理可得y=
综上所述:当点G在线段OD上时,y=
当点G在线段OB上时,y=
同课章节目录
