4.5利用三角形全等测距离 北师大版初中数学七年级下册同步练习(含解析)
文档属性
| 名称 | 4.5利用三角形全等测距离 北师大版初中数学七年级下册同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 407.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 11:16:37 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.5利用三角形全等测距离北师大版初中数学七年级下册同步练习
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
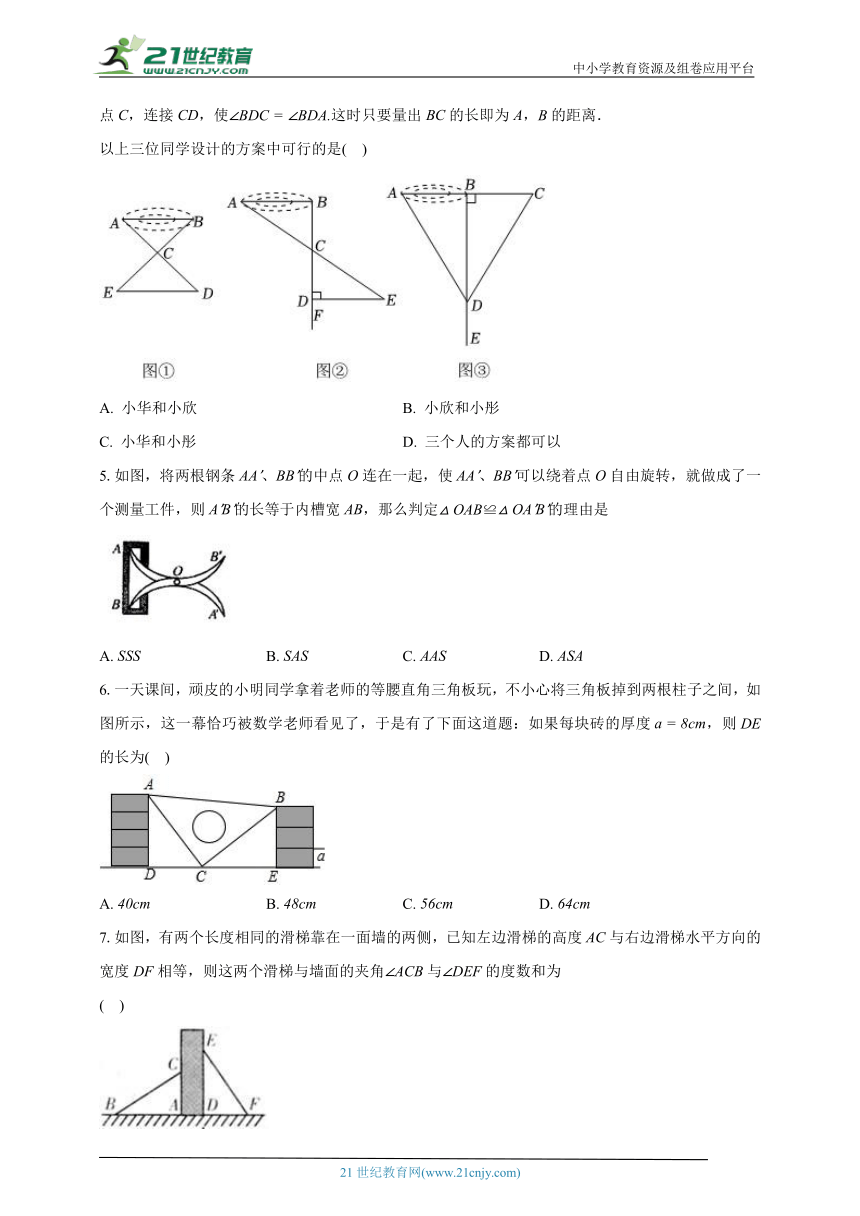
1.王强同学用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板,点在上,点和分别与木墙的顶端重合则两堵木墙之间的距离是( )
A. B. C. D.
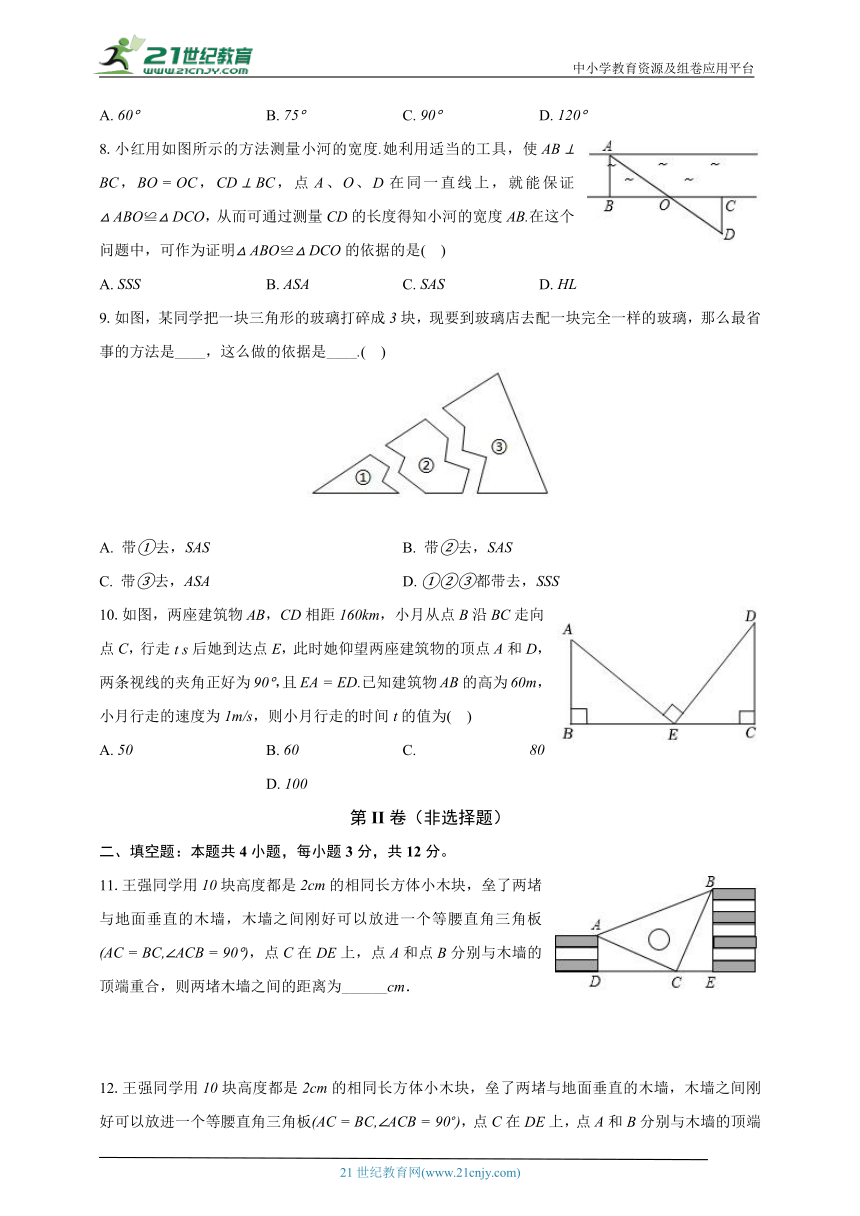
2.小明在学习了全等三角形的相关知识后,发现了一种测量距离的方法,如图,小明直立在河岸边的处,他压低帽子帽沿,使视线通过帽沿,恰好落在河对岸的处,然后转过身,保持和刚才完全一样的姿势,这时视线落在水平地面的处三点在同一水平直线上,小明通过测量,之间的距离,即得到,之间的距离.小明这种方法的原理是( )
A. B. C. D.
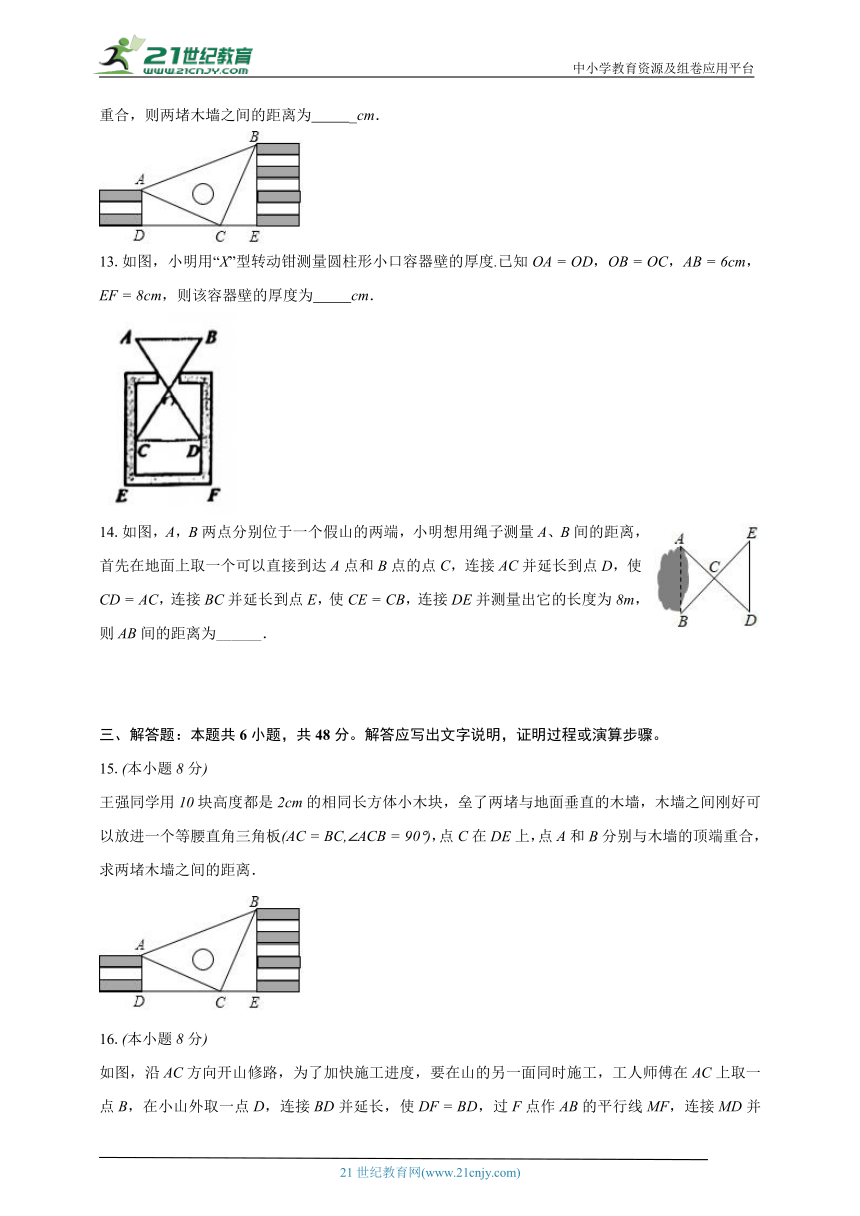
3.一块三角形玻璃被小红碰碎成四块,如图,小红打算只带其中的两块去玻璃店并买回一块和以前一样的玻璃,她需要( )
A. 带其中的任意两块 B. 带,或,就可以了
C. 带,或,就可以了 D. 带,或,或,均可
4.综合实践活动小组为测量池塘两端,的距离,活动小组的三位同学分别设计出如下三种方案:
小华:如图,先在平地上取一个点,从点不经过池塘可以直接到达点和连接并延长到点,使,连接并延长到点,使,连接,量出的长即为,的距离.
小欣:如图,先过点作的垂线,在上取,两点,使,再过点作的垂线,交的延长线于点,则量出的长即为,的距离.
小彤:如图,过点作的垂线,在上取一点,连接,然后在的延长线上取一点,连接,使这时只要量出的长即为,的距离.
以上三位同学设计的方案中可行的是( )
A. 小华和小欣 B. 小欣和小彤
C. 小华和小彤 D. 三个人的方案都可以
5.如图,将两根钢条、的中点连在一起,使、可以绕着点自由旋转,就做成了一个测量工件,则的长等于内槽宽,那么判定≌的理由是
A. B. C. D.
6.一天课间,顽皮的小明同学拿着老师的等腰直角三角板玩,不小心将三角板掉到两根柱子之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题:如果每块砖的厚度,则的长为( )
A. B. C. D.
7.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度与右边滑梯水平方向的宽度相等,则这两个滑梯与墙面的夹角与的度数和为
( )
A. B. C. D.
8.小红用如图所示的方法测量小河的宽度她利用适当的工具,使,,,点、、在同一直线上,就能保证≌,从而可通过测量的长度得知小河的宽度在这个问题中,可作为证明≌的依据的是( )
A. B. C. D.
9.如图,某同学把一块三角形的玻璃打碎成块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是____,这么做的依据是____( )
A. 带去, B. 带去,
C. 带去, D. 都带去,
10.如图,两座建筑物,相距,小月从点沿走向点,行走后她到达点,此时她仰望两座建筑物的顶点和,两条视线的夹角正好为,且已知建筑物的高为,小月行走的速度为,则小月行走的时间的值为( )
A. B. C. D.
第II卷(非选择题)
二、填空题:本题共4小题,每小题3分,共12分。
11.王强同学用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板,点在上,点和点分别与木墙的顶端重合,则两堵木墙之间的距离为______.
12.王强同学用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板,点在上,点和分别与木墙的顶端重合,则两堵木墙之间的距离为 .
13.如图,小明用“”型转动钳测量圆柱形小口容器壁的厚度已知,,,,则该容器壁的厚度为 .
14.如图,,两点分别位于一个假山的两端,小明想用绳子测量、间的距离,首先在地面上取一个可以直接到达点和点的点,连接并延长到点,使,连接并延长到点,使,连接并测量出它的长度为,则间的距离为______.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
王强同学用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板,点在上,点和分别与木墙的顶端重合,求两堵木墙之间的距离.
16.本小题分
如图,沿方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在上取一点,在小山外取一点,连接并延长,使,过点作的平行线,连接并延长,在延长线上取一点,使,在点开工就能使,,成一条直线,你知道其中的道理吗?
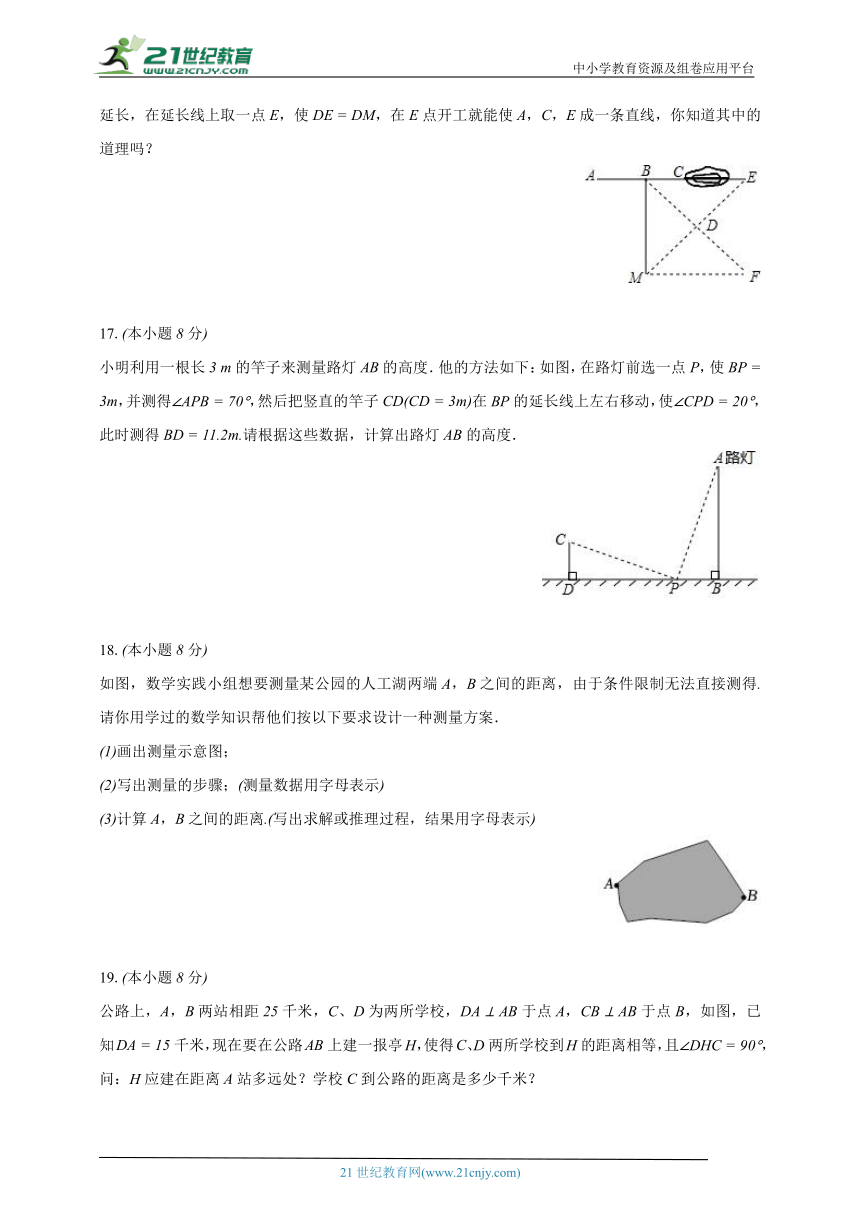
17.本小题分
小明利用一根长的竿子来测量路灯的高度.他的方法如下:如图,在路灯前选一点,使,并测得,然后把竖直的竿子在的延长线上左右移动,使,此时测得请根据这些数据,计算出路灯的高度.
18.本小题分
如图,数学实践小组想要测量某公园的人工湖两端,之间的距离,由于条件限制无法直接测得请你用学过的数学知识帮他们按以下要求设计一种测量方案.
画出测量示意图;
写出测量的步骤;测量数据用字母表示
计算,之间的距离写出求解或推理过程,结果用字母表示
19.本小题分
公路上,,两站相距千米,、为两所学校,于点,于点,如图,已知千米,现在要在公路上建一报亭,使得、两所学校到的距离相等,且,问:应建在距离站多远处?学校到公路的距离是多少千米?
20.本小题分
生活中的数学:
启迪中学计划为现初一学生暑期军训配备如图所示的折叠凳,这样设计的折叠発坐着舒适、稳定,这种设计所运用的数学原理是______.
图是折叠凳撑开后的侧面示意图木条等材料宽度忽略不计,其中凳腿和的长相等,是它们的中点为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度设计为,则由以上信息可推得的长度也为,请说明的理由.
答案和解析
1.【答案】
【解析】解:,,,,
,
,,
,
在和中,
,
≌;
,,
,
故选:.
由题意易得,则有,进而可证≌,然后根据全等三角形的性质求解即可.
本题主要考查全等三角形的性质与判定,熟练掌握三角形全等的判定条件是解题的关键.
2.【答案】
【解析】解:,
,
在与中,
,
≌,
,
故选:.
根据垂直的定义和全等三角形的判定和性质定理即可得到结论.
本题考查了全等三角形的应用,熟练掌握全等三角形的判定和性质定理是解题的关键.
3.【答案】
【解析】想要买一块和以前一样的玻璃,只要确定一个角及两条边或两个角及一条边即可.
【详解】解:由图可知,带上和相当于有两个角和一条边,所以可得两块三角形玻璃全等;同理,带上和也相当于有两角夹一边,同样也可以得三角形全等;和中,确定了上边的角的大小及两边的方向,又确定了底边的方向,继而可得全等;
故选:
【点睛】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法,联系实际,灵活运用所学知识是解题的关键.
4.【答案】
【解析】解:小华同学的方案:
在和中,
,
≌,
,
小华同学的方案可行;
小欣同学的方案:
在和中,
,
≌
,
小欣同学的方案可行;
小彤同学的方案:
在和中,
,
≌
,
小彤同学的方案可行.
故选:.
小华同学利用的是“边角边”,小欣和小彤同学的方案利用的是“角边角”.
本题主要考查了全等三角形的应用,熟练掌握全等三角形判定的“”和“”定理是解决问题的关键.
5.【答案】
【解析】【分析】
此题主要考查全等三角形的判定方法,此题利用了,做题时要认真读图,找出有用的条件是十分必要的.由于已知是、的中点,再加对顶角相等即可证明≌,所以全等理由就可以知道了.
【解答】
解:与中,
,
≌.
故选B.
6.【答案】
【解析】解:由题意得,,
,
在和中,
,
≌,
,,
,
,
,
,
故选:.
由等腰直角三角形的性质可得,,因此可以考虑证明和全等,可以证明的长为块砖的厚度的和.
此题考查全等三角形的判定与性质、等腰直角三角形的性质,此题是与三角形全等有关的应用题,是很好的练习题.
7.【答案】
【解析】【分析】
本题考查的是全等三角形的判定及性质,直角三角形的性质。先根据,判断出≌,再根据全等三角形的性质可知,有两对相等的角,再由直角三角形的两锐角互余即可解答。
【解答】
解:如图,
滑梯、墙、地面正好构成直角三角形
在和中
,
≌
故选C。
8.【答案】
【解析】【分析】
此题主要考查了全等三角形的判定,正确掌握全等三角形的判定方法是解题关键.
直接利用全等三角形的判定方法得出符合题意的答案.
【解答】
解:,,
,
在和中,
,
≌,
则证明≌的依据的是,
故选:.
9.【答案】
【解析】解:根据三角形全等的判定方法,根据角边角可确定一个全等三角形,
只有第三块玻璃包括了两角和它们的夹边,利用得出全等,只有带去才能配一块完全一样的玻璃,是符合题意的.
故选:.
根据全等三角形的判定,已知两角和夹边,就可以确定一个三角形.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:、、、、,做题时要根据已知条件进行选择运用.
10.【答案】
【解析】解:,
.
,
.
,
在和中
,
≌,
.
,
.
小月走的时间是.
故选:.
直接利用全等三角形的判定方法得出≌,进而得出的长即可得出答案.
此题主要考查了全等三角形的应用,正确得出≌是解题关键.
11.【答案】
【解析】【分析】
此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.
根据题意可得,,,,进而得到,再根据同角的余角相等可得,再证明≌即可,利用全等三角形的性质进行解答.
【解答】
解:由题意得:,,,,
,
,,
,
在和中,
≌;
由题意得:,,
,,
,
答:两堵木墙之间的距离为.
故答案为:.
12.【答案】
【解析】【考点】全等三角形的应用
【分析】根据题意可得,,,,进而得到,再根据等角的余角相等可得,再证明即可,利用全等三角形的性质进行解答.
【解答】解:由题意得:,,,,
,
,,
,
在和中,
;
由题意得:,,
,
答:两堵木墙之间的距离为.
故答案为:.
【点评】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.
13.【答案】
【解析】解:在和中,
,
≌,
,
,
圆柱形容器的壁厚是,
故答案为.
只要证明≌,可得,即可解决问题.
本题考查全等三角形的应用,根据全等三角形判定证得≌是解决问题的关键.
14.【答案】
【解析】解:在和中,
,
≌,
,
故答案为:.
根据全等三角形的判定和性质即可得到结论.
本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.
15.【答案】解:由题意得:,,,,
,
,,
,
在和中,
≌;
由题意得:,,
,
答:两堵木墙之间的距离为.
【解析】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.
根据题意可得,,,,进而得到,再根据等角的余角相等可得,再证明≌即可,利用全等三角形的性质进行解答.
16.【答案】解:在和中,
≌,
,
,
,
、、三点在一条直线上.
【解析】【分析】
首先证明≌,可得,进而得到,再由可得、、三点在一条直线上.
此题主要考查了全等三角形的应用,关键是正确理解题意,证明.
17.【答案】解:,,,
.
在和中,
≌,
.
,,
,
即.
答:路灯的高度是.
【解析】此题主要考查了全等三角形的应用,根据题意得出≌是解题关键.
根据题意可得≌,进而利用求出即可.
18.【答案】解:测量示意图如图所示;
在湖岸上找可以直接到达,的一点,连接并延长到使,连接并延长到点使,连接,则测量的长度,即为的长度为;
设,
由测量方案可得,,
在和中,
,
≌ ,
.
【解析】根据题意画出图形即可;
根据作图的作法写出步骤即可;
根据全等三角形的判定和性质定理即可得到结论.
本题考查了全等三角形的应用;解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.
19.【答案】解:,
,
,
,
,
在和中,,
≌,
千米,,
,两站相距千米,
千米,
千米,
学校到公路的距离是千米.
答:应建在距离站千米处,学校到公路的距离是千米.
【解析】根据同角的余角相等求出,再利用“角角边”证明和全等,根据全等三角形对应边相等可得,,再根据计算即可得解.
本题考查了全等三角形的应用,全等三角形的性质,熟练掌握全等三角形的判定方法求出两三角形全等是解题的关键.
20.【答案】三角形具有稳定性;
证明:是和的中点,
,,
在和中,
,
≌,
.
【解析】解:这种设计所运用的数学原理是三角形具有稳定性,
故答案为:三角形具有稳定性;
见答案.
利用三角形的性质进行解答;
利用定理判定≌,再利用全等三角形的性质可得答案.
此题主要考查了全等三角形的应用,以及三角形的性质,关键是掌握全等三角形的判定方法和性质定理.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.5利用三角形全等测距离北师大版初中数学七年级下册同步练习
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.王强同学用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板,点在上,点和分别与木墙的顶端重合则两堵木墙之间的距离是( )
A. B. C. D.
2.小明在学习了全等三角形的相关知识后,发现了一种测量距离的方法,如图,小明直立在河岸边的处,他压低帽子帽沿,使视线通过帽沿,恰好落在河对岸的处,然后转过身,保持和刚才完全一样的姿势,这时视线落在水平地面的处三点在同一水平直线上,小明通过测量,之间的距离,即得到,之间的距离.小明这种方法的原理是( )
A. B. C. D.
3.一块三角形玻璃被小红碰碎成四块,如图,小红打算只带其中的两块去玻璃店并买回一块和以前一样的玻璃,她需要( )
A. 带其中的任意两块 B. 带,或,就可以了
C. 带,或,就可以了 D. 带,或,或,均可
4.综合实践活动小组为测量池塘两端,的距离,活动小组的三位同学分别设计出如下三种方案:
小华:如图,先在平地上取一个点,从点不经过池塘可以直接到达点和连接并延长到点,使,连接并延长到点,使,连接,量出的长即为,的距离.
小欣:如图,先过点作的垂线,在上取,两点,使,再过点作的垂线,交的延长线于点,则量出的长即为,的距离.
小彤:如图,过点作的垂线,在上取一点,连接,然后在的延长线上取一点,连接,使这时只要量出的长即为,的距离.
以上三位同学设计的方案中可行的是( )
A. 小华和小欣 B. 小欣和小彤
C. 小华和小彤 D. 三个人的方案都可以
5.如图,将两根钢条、的中点连在一起,使、可以绕着点自由旋转,就做成了一个测量工件,则的长等于内槽宽,那么判定≌的理由是
A. B. C. D.
6.一天课间,顽皮的小明同学拿着老师的等腰直角三角板玩,不小心将三角板掉到两根柱子之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题:如果每块砖的厚度,则的长为( )
A. B. C. D.
7.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度与右边滑梯水平方向的宽度相等,则这两个滑梯与墙面的夹角与的度数和为
( )
A. B. C. D.
8.小红用如图所示的方法测量小河的宽度她利用适当的工具,使,,,点、、在同一直线上,就能保证≌,从而可通过测量的长度得知小河的宽度在这个问题中,可作为证明≌的依据的是( )
A. B. C. D.
9.如图,某同学把一块三角形的玻璃打碎成块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是____,这么做的依据是____( )
A. 带去, B. 带去,
C. 带去, D. 都带去,
10.如图,两座建筑物,相距,小月从点沿走向点,行走后她到达点,此时她仰望两座建筑物的顶点和,两条视线的夹角正好为,且已知建筑物的高为,小月行走的速度为,则小月行走的时间的值为( )
A. B. C. D.
第II卷(非选择题)
二、填空题:本题共4小题,每小题3分,共12分。
11.王强同学用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板,点在上,点和点分别与木墙的顶端重合,则两堵木墙之间的距离为______.
12.王强同学用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板,点在上,点和分别与木墙的顶端重合,则两堵木墙之间的距离为 .
13.如图,小明用“”型转动钳测量圆柱形小口容器壁的厚度已知,,,,则该容器壁的厚度为 .
14.如图,,两点分别位于一个假山的两端,小明想用绳子测量、间的距离,首先在地面上取一个可以直接到达点和点的点,连接并延长到点,使,连接并延长到点,使,连接并测量出它的长度为,则间的距离为______.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
王强同学用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板,点在上,点和分别与木墙的顶端重合,求两堵木墙之间的距离.
16.本小题分
如图,沿方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在上取一点,在小山外取一点,连接并延长,使,过点作的平行线,连接并延长,在延长线上取一点,使,在点开工就能使,,成一条直线,你知道其中的道理吗?
17.本小题分
小明利用一根长的竿子来测量路灯的高度.他的方法如下:如图,在路灯前选一点,使,并测得,然后把竖直的竿子在的延长线上左右移动,使,此时测得请根据这些数据,计算出路灯的高度.
18.本小题分
如图,数学实践小组想要测量某公园的人工湖两端,之间的距离,由于条件限制无法直接测得请你用学过的数学知识帮他们按以下要求设计一种测量方案.
画出测量示意图;
写出测量的步骤;测量数据用字母表示
计算,之间的距离写出求解或推理过程,结果用字母表示
19.本小题分
公路上,,两站相距千米,、为两所学校,于点,于点,如图,已知千米,现在要在公路上建一报亭,使得、两所学校到的距离相等,且,问:应建在距离站多远处?学校到公路的距离是多少千米?
20.本小题分
生活中的数学:
启迪中学计划为现初一学生暑期军训配备如图所示的折叠凳,这样设计的折叠発坐着舒适、稳定,这种设计所运用的数学原理是______.
图是折叠凳撑开后的侧面示意图木条等材料宽度忽略不计,其中凳腿和的长相等,是它们的中点为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度设计为,则由以上信息可推得的长度也为,请说明的理由.
答案和解析
1.【答案】
【解析】解:,,,,
,
,,
,
在和中,
,
≌;
,,
,
故选:.
由题意易得,则有,进而可证≌,然后根据全等三角形的性质求解即可.
本题主要考查全等三角形的性质与判定,熟练掌握三角形全等的判定条件是解题的关键.
2.【答案】
【解析】解:,
,
在与中,
,
≌,
,
故选:.
根据垂直的定义和全等三角形的判定和性质定理即可得到结论.
本题考查了全等三角形的应用,熟练掌握全等三角形的判定和性质定理是解题的关键.
3.【答案】
【解析】想要买一块和以前一样的玻璃,只要确定一个角及两条边或两个角及一条边即可.
【详解】解:由图可知,带上和相当于有两个角和一条边,所以可得两块三角形玻璃全等;同理,带上和也相当于有两角夹一边,同样也可以得三角形全等;和中,确定了上边的角的大小及两边的方向,又确定了底边的方向,继而可得全等;
故选:
【点睛】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法,联系实际,灵活运用所学知识是解题的关键.
4.【答案】
【解析】解:小华同学的方案:
在和中,
,
≌,
,
小华同学的方案可行;
小欣同学的方案:
在和中,
,
≌
,
小欣同学的方案可行;
小彤同学的方案:
在和中,
,
≌
,
小彤同学的方案可行.
故选:.
小华同学利用的是“边角边”,小欣和小彤同学的方案利用的是“角边角”.
本题主要考查了全等三角形的应用,熟练掌握全等三角形判定的“”和“”定理是解决问题的关键.
5.【答案】
【解析】【分析】
此题主要考查全等三角形的判定方法,此题利用了,做题时要认真读图,找出有用的条件是十分必要的.由于已知是、的中点,再加对顶角相等即可证明≌,所以全等理由就可以知道了.
【解答】
解:与中,
,
≌.
故选B.
6.【答案】
【解析】解:由题意得,,
,
在和中,
,
≌,
,,
,
,
,
,
故选:.
由等腰直角三角形的性质可得,,因此可以考虑证明和全等,可以证明的长为块砖的厚度的和.
此题考查全等三角形的判定与性质、等腰直角三角形的性质,此题是与三角形全等有关的应用题,是很好的练习题.
7.【答案】
【解析】【分析】
本题考查的是全等三角形的判定及性质,直角三角形的性质。先根据,判断出≌,再根据全等三角形的性质可知,有两对相等的角,再由直角三角形的两锐角互余即可解答。
【解答】
解:如图,
滑梯、墙、地面正好构成直角三角形
在和中
,
≌
故选C。
8.【答案】
【解析】【分析】
此题主要考查了全等三角形的判定,正确掌握全等三角形的判定方法是解题关键.
直接利用全等三角形的判定方法得出符合题意的答案.
【解答】
解:,,
,
在和中,
,
≌,
则证明≌的依据的是,
故选:.
9.【答案】
【解析】解:根据三角形全等的判定方法,根据角边角可确定一个全等三角形,
只有第三块玻璃包括了两角和它们的夹边,利用得出全等,只有带去才能配一块完全一样的玻璃,是符合题意的.
故选:.
根据全等三角形的判定,已知两角和夹边,就可以确定一个三角形.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:、、、、,做题时要根据已知条件进行选择运用.
10.【答案】
【解析】解:,
.
,
.
,
在和中
,
≌,
.
,
.
小月走的时间是.
故选:.
直接利用全等三角形的判定方法得出≌,进而得出的长即可得出答案.
此题主要考查了全等三角形的应用,正确得出≌是解题关键.
11.【答案】
【解析】【分析】
此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.
根据题意可得,,,,进而得到,再根据同角的余角相等可得,再证明≌即可,利用全等三角形的性质进行解答.
【解答】
解:由题意得:,,,,
,
,,
,
在和中,
≌;
由题意得:,,
,,
,
答:两堵木墙之间的距离为.
故答案为:.
12.【答案】
【解析】【考点】全等三角形的应用
【分析】根据题意可得,,,,进而得到,再根据等角的余角相等可得,再证明即可,利用全等三角形的性质进行解答.
【解答】解:由题意得:,,,,
,
,,
,
在和中,
;
由题意得:,,
,
答:两堵木墙之间的距离为.
故答案为:.
【点评】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.
13.【答案】
【解析】解:在和中,
,
≌,
,
,
圆柱形容器的壁厚是,
故答案为.
只要证明≌,可得,即可解决问题.
本题考查全等三角形的应用,根据全等三角形判定证得≌是解决问题的关键.
14.【答案】
【解析】解:在和中,
,
≌,
,
故答案为:.
根据全等三角形的判定和性质即可得到结论.
本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.
15.【答案】解:由题意得:,,,,
,
,,
,
在和中,
≌;
由题意得:,,
,
答:两堵木墙之间的距离为.
【解析】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.
根据题意可得,,,,进而得到,再根据等角的余角相等可得,再证明≌即可,利用全等三角形的性质进行解答.
16.【答案】解:在和中,
≌,
,
,
,
、、三点在一条直线上.
【解析】【分析】
首先证明≌,可得,进而得到,再由可得、、三点在一条直线上.
此题主要考查了全等三角形的应用,关键是正确理解题意,证明.
17.【答案】解:,,,
.
在和中,
≌,
.
,,
,
即.
答:路灯的高度是.
【解析】此题主要考查了全等三角形的应用,根据题意得出≌是解题关键.
根据题意可得≌,进而利用求出即可.
18.【答案】解:测量示意图如图所示;
在湖岸上找可以直接到达,的一点,连接并延长到使,连接并延长到点使,连接,则测量的长度,即为的长度为;
设,
由测量方案可得,,
在和中,
,
≌ ,
.
【解析】根据题意画出图形即可;
根据作图的作法写出步骤即可;
根据全等三角形的判定和性质定理即可得到结论.
本题考查了全等三角形的应用;解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.
19.【答案】解:,
,
,
,
,
在和中,,
≌,
千米,,
,两站相距千米,
千米,
千米,
学校到公路的距离是千米.
答:应建在距离站千米处,学校到公路的距离是千米.
【解析】根据同角的余角相等求出,再利用“角角边”证明和全等,根据全等三角形对应边相等可得,,再根据计算即可得解.
本题考查了全等三角形的应用,全等三角形的性质,熟练掌握全等三角形的判定方法求出两三角形全等是解题的关键.
20.【答案】三角形具有稳定性;
证明:是和的中点,
,,
在和中,
,
≌,
.
【解析】解:这种设计所运用的数学原理是三角形具有稳定性,
故答案为:三角形具有稳定性;
见答案.
利用三角形的性质进行解答;
利用定理判定≌,再利用全等三角形的性质可得答案.
此题主要考查了全等三角形的应用,以及三角形的性质,关键是掌握全等三角形的判定方法和性质定理.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
