5.4利用轴对称进行设计 北师大版初中数学七年级下册同步练习(含解析)
文档属性
| 名称 | 5.4利用轴对称进行设计 北师大版初中数学七年级下册同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 634.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-07 09:35:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
5.4利用轴对称进行设计北师大版初中数学七年级下册同步练习
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图是用七巧板拼接成的一个轴对称图形忽略拼接线,小亮改变的位置,将分别摆放在图中左、下、右的位置摆放时无缝隙、不重叠,还能拼接成不同轴对称图形的个数为( )
A. B. C. D.
2.如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在图中与成轴对称的格点三角形可以画出
( )
A. 个 B. 个 C. 个 D. 个
3.下列图形中,不能由其中一部分通过轴对称变换得到的是( )
A. B. C. D.
4.第届亚运会于年月日年月日在中华人民共和国杭州市举行,在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案,其中可以看作是轴对称图形的是( )
A. B. C. D.
5.将一等腰直角三角形纸片对折后再对折,得到如图所示的图形,然后将阴影部分剪掉,把剩余部分展开后的平面图形是( )
A. B. C. D.
6.下列四个图案中,可以看作轴对称图形的是( )
A. B. C. D.
7.图的图案是由图中五种基本图形中的两种拼接而成,这两种基本图形是( )
A. B. C. D.
8.作已知点关于某直线的对称点的第一步是( )
A. 过已知点作一条直线与已知直线相交 B. 过已知点作一条直线与已知直线垂直
C. 过已知点作一条直线与已知直线平行 D. 不确定
9.如图,在正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在图中可以画出与成轴对称的格点三角形的个数为
( )
A. 个 B. 个 C. 个 D. 个
10.在下列方格中有五个同样大小的正方形如图摆放,请你添加一个正方形到空白方格中,使它与其余五个正方形组成的新图形是一个轴对称图形,这样的添法共有( )
A. 种 B. 种 C. 种 D. 种
第II卷(非选择题)
二、填空题:本题共4小题,每小题3分,共12分。
11.如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形,则把阴影涂在图中标有数字 的格子内.
12.如图所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图所示方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用个这样的图形图拼出来的图形的总长度是______结果用含,代数式表示.
13.如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的为格点三角形,在图中最多能画出_____个格点三角形与成轴对称.
14.如图,正方形网格中,已有两个小正方形被涂黑,再将图其余小正方形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有______个.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在平面直角坐标系中,每个小正方形的边长均为,点的坐标为,点的坐标为,点的坐标为.
作出关于轴对称的其中,,分别是,,的对应点不要求写作法
写出,,的坐标
在轴上找一点,使得的值最小要求写作法.
16.本小题分
在平面直角坐标系中,的顶点坐标,,.
在图中作出关于轴对称的图形;
在轴上找一个点,使得的周长最小,在图中标出点的位置;
求的面积.
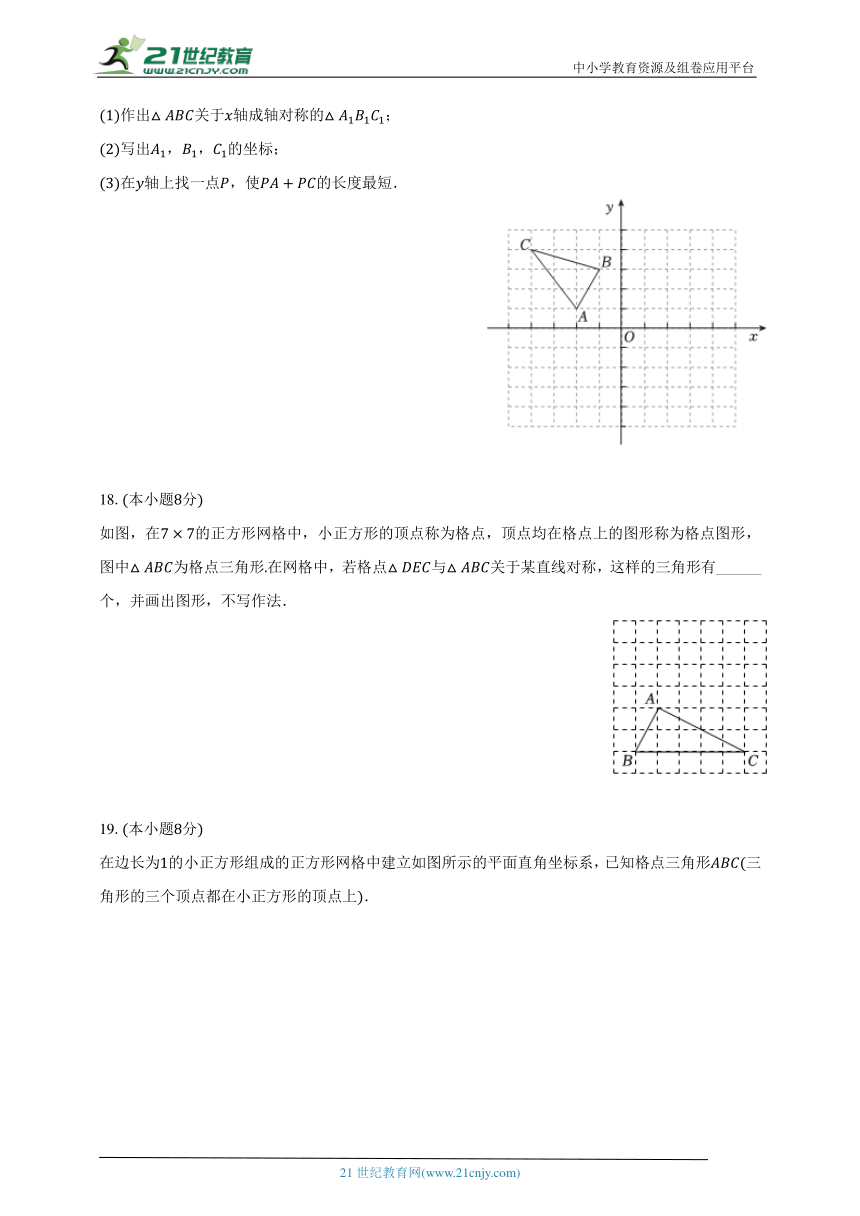
17.本小题分
如图,在平面直角坐标系中,,,.
作出关于轴成轴对称的;
写出,,的坐标;
在轴上找一点,使的长度最短.
18.本小题分
如图,在的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中为格点三角形在网格中,若格点与关于某直线对称,这样的三角形有______个,并画出图形,不写作法.
19.本小题分
在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形三角形的三个顶点都在小正方形的顶点上.
画出关于轴对称的;
写出点、、的坐标;
在轴上找点,使最小,请你标出点的位置并求出点的坐标.
20.本小题分
如图,在平面直角坐标系中,其顶点坐标如下:,,.
作出关于轴对称的图形,其中,,分别和,,对应,则的坐标为______,的坐标为______的坐标为______,线段的长度为______;
仅用直尺在轴上确定点的位置:使得点到点、点的距离之和最小.
答案和解析
1.【答案】
【解析】解:观察图象可知,能拼接成不同轴对称图形的个数为个.
故选:.
能拼接为等腰梯形,等腰直角三角形,矩形,由此即可判断.
本题考查利用轴对称设计图案,解题的关键是理解轴对称图形的性质,属于中考常考题型.
2.【答案】
【解析】如图,最多能画出个格点三角形与成轴对称.
故选A.
3.【答案】
【解析】解:、是轴对称图形,
不符合题意;
B、是轴对称图形,
不符合题意;
C、不是轴对称图形,
符合题意;
D、是轴对称图形,
不符合题意;
故选:.
根据轴对称图形的定义和轴对称变换判断选择即可.
本题考查了轴对称图形即沿着某条直线折叠,直线两旁的部分完全重合;熟练掌握定义是解题的关键.
4.【答案】
【解析】解:,,选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项中的图形都能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:.
根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
此题主要考查了轴对称图形,关键是掌握如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴.
5.【答案】
【解析】【分析】
本题考查了剪纸问题,作图轴对称变换,运用轴对称变换的作图方法作图即可判断答案.
【解答】
解:如下图,把题干中的第三个图形,按照原折叠方向的反方向,沿直线和进行轴对称变换,得出阴影部分的位置和形状图,再去掉阴影部分即为展开后的平面图形图,
因此只有选项的图形符合题意.
故选A.
6.【答案】
【解析】解:、不是轴对称图形,不符合题意;
B、是轴对称图形,符合题意;
C、不是轴对称图形,不符合题意;
D、不是轴对称图形,不符合题意;
故选:.
根据轴对称图形的概念进行判断即可.
本题考查轴对称图形的识别,解题关键是抓住轴对称图形是指将一个图形沿着某条直线折叠,直线两旁的部分能够完全重合.
7.【答案】
【解析】解:根据图结合轴对称图形的特征,可以判断是由两个图形拼接而成,故选B.
8.【答案】
【解析】【详解】作已知点关于某直线的对称点的第一步是过已知点作一条直线与已知直线垂直,
故选B.
9.【答案】
【解析】解:如图所示:
故选:.
根据网格结构分别确定出不同的对称轴,然后作出成轴对称的三角形即可得解.
本题考查的是轴对称的相关概念,根据题意作出图形是解答此题的关键.
10.【答案】
【解析】【分析】
本题考查的是利用轴对称设计图案,解答此题要明确轴对称的性质,并据此构造出轴对称图形.
因为中间个小正方形组成一个大的正方形,正方形有四条对称轴,试着利用这四条对称轴添加图形得出答案即可.
【解答】
解:如图所示这样的添法共有种.
11.【答案】
【解析】【分析】
本题考查的是作简单平面图形轴对称后的图形,其依据是轴对称的性质,基本作法:先确定图形的关键点;利用轴对称性质作出关键点的对称点;按原图形中的方式顺次连接对称点.从阴影部分图形的各顶点向虚线作垂线并延长相同的距离找对应点,然后顺次连接各点可得答案.
【解答】
解:如图所示,
把阴影凃在图中标有数字的格子内所组成的图形是轴对称图形.
12.【答案】
【解析】【分析】
本题主要考查了利用轴对称设计图案和列代数式,利用轴对称设计图案关键是要熟悉轴对称的性质,属于较易题.
用个这样的图形图的总长减去拼接时的重叠部分,即可得到拼出来的图形的总长度.
【解答】
解:由图可得,拼出来的图形的总长度.
故答案为:.
13.【答案】
【解析】解:如图,最多能画出个格点三角形与成轴对称.
故答案为:.
根据网格结构分别确定出不同的对称轴,然后作出轴对称三角形即可得解
本题考查了利用轴对称变换作图,熟练掌握网格结构并准确找出对应点的位置是解题的关键,本题难点在于确定出不同的对称轴.
14.【答案】
【解析】【分析】
本题考查了利用轴对称设计图案的知识,关键是掌握好轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
根据轴对称的概念作答.如果一个图形沿一条直线对折,直线两旁的部分能互相重合,那么这个图形叫做轴对称图形.
【解答】
解:选择一个正方形涂黑,使得个涂黑的正方形组成轴对称图形,
选择的位置有以下几种:处,处,处,处,处,选择的位置共有处.
故答案为:
15.【答案】解:如图所示,即为所求;
由题意可得:,,;
找到点关于轴的对称点,连接交轴于点,此时的值最小,即可得解.
【解析】本题考查作图轴对称变换,解题的关键是掌握轴对称变换的定义和性质,并据此得出变换后的对应点.
分别作出三个顶点关于轴的对称点,再首尾顺次连接即可得;
根据所作图形可得各顶点坐标;
找到点关于轴的对称点,连接交轴于点,此时的值最小,即可得解.
16.【答案】解:如图所示,即为所求;
如图所示,点即为所求;
;
【解析】根据关于轴对称的点横坐标互为相反数,纵坐标相同找到、、对应点、、的位置,然后顺次连接、、即可;
根据轴对称的性质,连接,交轴于点,点即为所求;
利用割补法求解即可.
本题主要考查了坐标与图形变化轴对称,轴对称最短路径问题,网格中求三角形面积,解题的关键是理解题意,正确作出图形.
17.【答案】解:如图,即为所求;
,,,,;
如图,点即为所求.
【解析】根据轴对称的性质即可作出关于轴成轴对称的;
结合即可写出,,的坐标;
找到点关于轴的对称点,连接交轴于点,即可使的长度最短.
本题考查作图轴对称变换,轴对称最短路线问题,解决本题的关键是掌握轴对称的性质.
18.【答案】
【解析】解:如图,、、为所作.
故答案为:.
以直线为对称轴得到,以的垂直平分线为对称轴得到,以的正方形网格的对角线所在直线为对称轴得到.
本题考查了作图轴对称变换:作轴对称后的图形的依据是轴对称的性质,掌握其基本作法是解决问题的关键先确定图形的关键点;利用轴对称性质作出关键点的对称点;按原图形中的方式顺次连接对称点.
19.【答案】解:如图所示,即为所求.
由图知,、、;
如图所示,点即为所求,.
【解析】分别作出三个顶点关于轴的对称点,再首尾顺次连接即可得答案;
根据所作图形可得答案;
连接,与轴的交点即为所求,结合图形可得其坐标.
本题主要考查作图轴对称变换,解题的关键是掌握轴对称变换的定义与性质,并据此得出其对应点.
20.【答案】
【解析】解:如图所示,即为所求,,,,线段的长度为;
故答案为:;;;;
点的位置如图所示.
根据轴对称变换的性质找出对应点即可求解,根据图象直接得出的长度;
作点关于轴的对称点,连接交轴于点,则点即为所求.
本题考查了轴对称变换的性质,轴对称最短路线问题,熟练掌握轴对称变换的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.4利用轴对称进行设计北师大版初中数学七年级下册同步练习
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图是用七巧板拼接成的一个轴对称图形忽略拼接线,小亮改变的位置,将分别摆放在图中左、下、右的位置摆放时无缝隙、不重叠,还能拼接成不同轴对称图形的个数为( )
A. B. C. D.
2.如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在图中与成轴对称的格点三角形可以画出
( )
A. 个 B. 个 C. 个 D. 个
3.下列图形中,不能由其中一部分通过轴对称变换得到的是( )
A. B. C. D.
4.第届亚运会于年月日年月日在中华人民共和国杭州市举行,在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案,其中可以看作是轴对称图形的是( )
A. B. C. D.
5.将一等腰直角三角形纸片对折后再对折,得到如图所示的图形,然后将阴影部分剪掉,把剩余部分展开后的平面图形是( )
A. B. C. D.
6.下列四个图案中,可以看作轴对称图形的是( )
A. B. C. D.
7.图的图案是由图中五种基本图形中的两种拼接而成,这两种基本图形是( )
A. B. C. D.
8.作已知点关于某直线的对称点的第一步是( )
A. 过已知点作一条直线与已知直线相交 B. 过已知点作一条直线与已知直线垂直
C. 过已知点作一条直线与已知直线平行 D. 不确定
9.如图,在正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在图中可以画出与成轴对称的格点三角形的个数为
( )
A. 个 B. 个 C. 个 D. 个
10.在下列方格中有五个同样大小的正方形如图摆放,请你添加一个正方形到空白方格中,使它与其余五个正方形组成的新图形是一个轴对称图形,这样的添法共有( )
A. 种 B. 种 C. 种 D. 种
第II卷(非选择题)
二、填空题:本题共4小题,每小题3分,共12分。
11.如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形,则把阴影涂在图中标有数字 的格子内.
12.如图所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图所示方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用个这样的图形图拼出来的图形的总长度是______结果用含,代数式表示.
13.如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的为格点三角形,在图中最多能画出_____个格点三角形与成轴对称.
14.如图,正方形网格中,已有两个小正方形被涂黑,再将图其余小正方形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有______个.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
如图,在平面直角坐标系中,每个小正方形的边长均为,点的坐标为,点的坐标为,点的坐标为.
作出关于轴对称的其中,,分别是,,的对应点不要求写作法
写出,,的坐标
在轴上找一点,使得的值最小要求写作法.
16.本小题分
在平面直角坐标系中,的顶点坐标,,.
在图中作出关于轴对称的图形;
在轴上找一个点,使得的周长最小,在图中标出点的位置;
求的面积.
17.本小题分
如图,在平面直角坐标系中,,,.
作出关于轴成轴对称的;
写出,,的坐标;
在轴上找一点,使的长度最短.
18.本小题分
如图,在的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中为格点三角形在网格中,若格点与关于某直线对称,这样的三角形有______个,并画出图形,不写作法.
19.本小题分
在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形三角形的三个顶点都在小正方形的顶点上.
画出关于轴对称的;
写出点、、的坐标;
在轴上找点,使最小,请你标出点的位置并求出点的坐标.
20.本小题分
如图,在平面直角坐标系中,其顶点坐标如下:,,.
作出关于轴对称的图形,其中,,分别和,,对应,则的坐标为______,的坐标为______的坐标为______,线段的长度为______;
仅用直尺在轴上确定点的位置:使得点到点、点的距离之和最小.
答案和解析
1.【答案】
【解析】解:观察图象可知,能拼接成不同轴对称图形的个数为个.
故选:.
能拼接为等腰梯形,等腰直角三角形,矩形,由此即可判断.
本题考查利用轴对称设计图案,解题的关键是理解轴对称图形的性质,属于中考常考题型.
2.【答案】
【解析】如图,最多能画出个格点三角形与成轴对称.
故选A.
3.【答案】
【解析】解:、是轴对称图形,
不符合题意;
B、是轴对称图形,
不符合题意;
C、不是轴对称图形,
符合题意;
D、是轴对称图形,
不符合题意;
故选:.
根据轴对称图形的定义和轴对称变换判断选择即可.
本题考查了轴对称图形即沿着某条直线折叠,直线两旁的部分完全重合;熟练掌握定义是解题的关键.
4.【答案】
【解析】解:,,选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项中的图形都能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:.
根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
此题主要考查了轴对称图形,关键是掌握如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴.
5.【答案】
【解析】【分析】
本题考查了剪纸问题,作图轴对称变换,运用轴对称变换的作图方法作图即可判断答案.
【解答】
解:如下图,把题干中的第三个图形,按照原折叠方向的反方向,沿直线和进行轴对称变换,得出阴影部分的位置和形状图,再去掉阴影部分即为展开后的平面图形图,
因此只有选项的图形符合题意.
故选A.
6.【答案】
【解析】解:、不是轴对称图形,不符合题意;
B、是轴对称图形,符合题意;
C、不是轴对称图形,不符合题意;
D、不是轴对称图形,不符合题意;
故选:.
根据轴对称图形的概念进行判断即可.
本题考查轴对称图形的识别,解题关键是抓住轴对称图形是指将一个图形沿着某条直线折叠,直线两旁的部分能够完全重合.
7.【答案】
【解析】解:根据图结合轴对称图形的特征,可以判断是由两个图形拼接而成,故选B.
8.【答案】
【解析】【详解】作已知点关于某直线的对称点的第一步是过已知点作一条直线与已知直线垂直,
故选B.
9.【答案】
【解析】解:如图所示:
故选:.
根据网格结构分别确定出不同的对称轴,然后作出成轴对称的三角形即可得解.
本题考查的是轴对称的相关概念,根据题意作出图形是解答此题的关键.
10.【答案】
【解析】【分析】
本题考查的是利用轴对称设计图案,解答此题要明确轴对称的性质,并据此构造出轴对称图形.
因为中间个小正方形组成一个大的正方形,正方形有四条对称轴,试着利用这四条对称轴添加图形得出答案即可.
【解答】
解:如图所示这样的添法共有种.
11.【答案】
【解析】【分析】
本题考查的是作简单平面图形轴对称后的图形,其依据是轴对称的性质,基本作法:先确定图形的关键点;利用轴对称性质作出关键点的对称点;按原图形中的方式顺次连接对称点.从阴影部分图形的各顶点向虚线作垂线并延长相同的距离找对应点,然后顺次连接各点可得答案.
【解答】
解:如图所示,
把阴影凃在图中标有数字的格子内所组成的图形是轴对称图形.
12.【答案】
【解析】【分析】
本题主要考查了利用轴对称设计图案和列代数式,利用轴对称设计图案关键是要熟悉轴对称的性质,属于较易题.
用个这样的图形图的总长减去拼接时的重叠部分,即可得到拼出来的图形的总长度.
【解答】
解:由图可得,拼出来的图形的总长度.
故答案为:.
13.【答案】
【解析】解:如图,最多能画出个格点三角形与成轴对称.
故答案为:.
根据网格结构分别确定出不同的对称轴,然后作出轴对称三角形即可得解
本题考查了利用轴对称变换作图,熟练掌握网格结构并准确找出对应点的位置是解题的关键,本题难点在于确定出不同的对称轴.
14.【答案】
【解析】【分析】
本题考查了利用轴对称设计图案的知识,关键是掌握好轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
根据轴对称的概念作答.如果一个图形沿一条直线对折,直线两旁的部分能互相重合,那么这个图形叫做轴对称图形.
【解答】
解:选择一个正方形涂黑,使得个涂黑的正方形组成轴对称图形,
选择的位置有以下几种:处,处,处,处,处,选择的位置共有处.
故答案为:
15.【答案】解:如图所示,即为所求;
由题意可得:,,;
找到点关于轴的对称点,连接交轴于点,此时的值最小,即可得解.
【解析】本题考查作图轴对称变换,解题的关键是掌握轴对称变换的定义和性质,并据此得出变换后的对应点.
分别作出三个顶点关于轴的对称点,再首尾顺次连接即可得;
根据所作图形可得各顶点坐标;
找到点关于轴的对称点,连接交轴于点,此时的值最小,即可得解.
16.【答案】解:如图所示,即为所求;
如图所示,点即为所求;
;
【解析】根据关于轴对称的点横坐标互为相反数,纵坐标相同找到、、对应点、、的位置,然后顺次连接、、即可;
根据轴对称的性质,连接,交轴于点,点即为所求;
利用割补法求解即可.
本题主要考查了坐标与图形变化轴对称,轴对称最短路径问题,网格中求三角形面积,解题的关键是理解题意,正确作出图形.
17.【答案】解:如图,即为所求;
,,,,;
如图,点即为所求.
【解析】根据轴对称的性质即可作出关于轴成轴对称的;
结合即可写出,,的坐标;
找到点关于轴的对称点,连接交轴于点,即可使的长度最短.
本题考查作图轴对称变换,轴对称最短路线问题,解决本题的关键是掌握轴对称的性质.
18.【答案】
【解析】解:如图,、、为所作.
故答案为:.
以直线为对称轴得到,以的垂直平分线为对称轴得到,以的正方形网格的对角线所在直线为对称轴得到.
本题考查了作图轴对称变换:作轴对称后的图形的依据是轴对称的性质,掌握其基本作法是解决问题的关键先确定图形的关键点;利用轴对称性质作出关键点的对称点;按原图形中的方式顺次连接对称点.
19.【答案】解:如图所示,即为所求.
由图知,、、;
如图所示,点即为所求,.
【解析】分别作出三个顶点关于轴的对称点,再首尾顺次连接即可得答案;
根据所作图形可得答案;
连接,与轴的交点即为所求,结合图形可得其坐标.
本题主要考查作图轴对称变换,解题的关键是掌握轴对称变换的定义与性质,并据此得出其对应点.
20.【答案】
【解析】解:如图所示,即为所求,,,,线段的长度为;
故答案为:;;;;
点的位置如图所示.
根据轴对称变换的性质找出对应点即可求解,根据图象直接得出的长度;
作点关于轴的对称点,连接交轴于点,则点即为所求.
本题考查了轴对称变换的性质,轴对称最短路线问题,熟练掌握轴对称变换的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
