(特别免费资源)高二数学算法案例(浙江省湖州市)
文档属性
| 名称 | (特别免费资源)高二数学算法案例(浙江省湖州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 25.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-06 10:31:00 | ||
图片预览

文档简介
高二数学算法案例
一、目标认知
学习目标:
1.理解辗转相除法与更相减损术中蕴含的数学原理,并能根据这些原理进行算法分析;
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序;
3.了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质;
4.了解各种进位制与十进制之间转换的规律,会利用各种进位制与十进制之间的联系进行各种进位制之间的转换.
重点:
1.理解辗转相除法与更相减损术求最大公约数的方法;
2.秦九韶算法的特点;
3.各进位制表示数的方法及各进位制之间的转换.
难点:
1.把辗转相除法与更相减损术的方法转换成程序框图与程序语言;
2.秦九韶算法的先进性理解;
3.除k去余法的理解以及各进位制之间转换的程序框图的设计.
二、知识要点梳理
知识点一:辗转相除法
也叫欧几里德算法,它是由欧几里德在公元前300年左右首先提出的.利用辗转相除法求最大公约数的步骤如下:
第一步:用较大的数m除以较小的数n得到一个商q0和一个余数r0;
第二步:若r0=0,则n为m,n的最大公约数;若r0≠0,则用除数n除以余数r0得到一个商q1和一个余数r1;
第三步:若r1=0,则r1为m,n的最大公约数;若r1≠0,则用除数r0除以余数r1得到一个商q2和一个余数r2;
……
依次计算直至rn=0,此时所得到的rn-1即为所求的最大公约数.
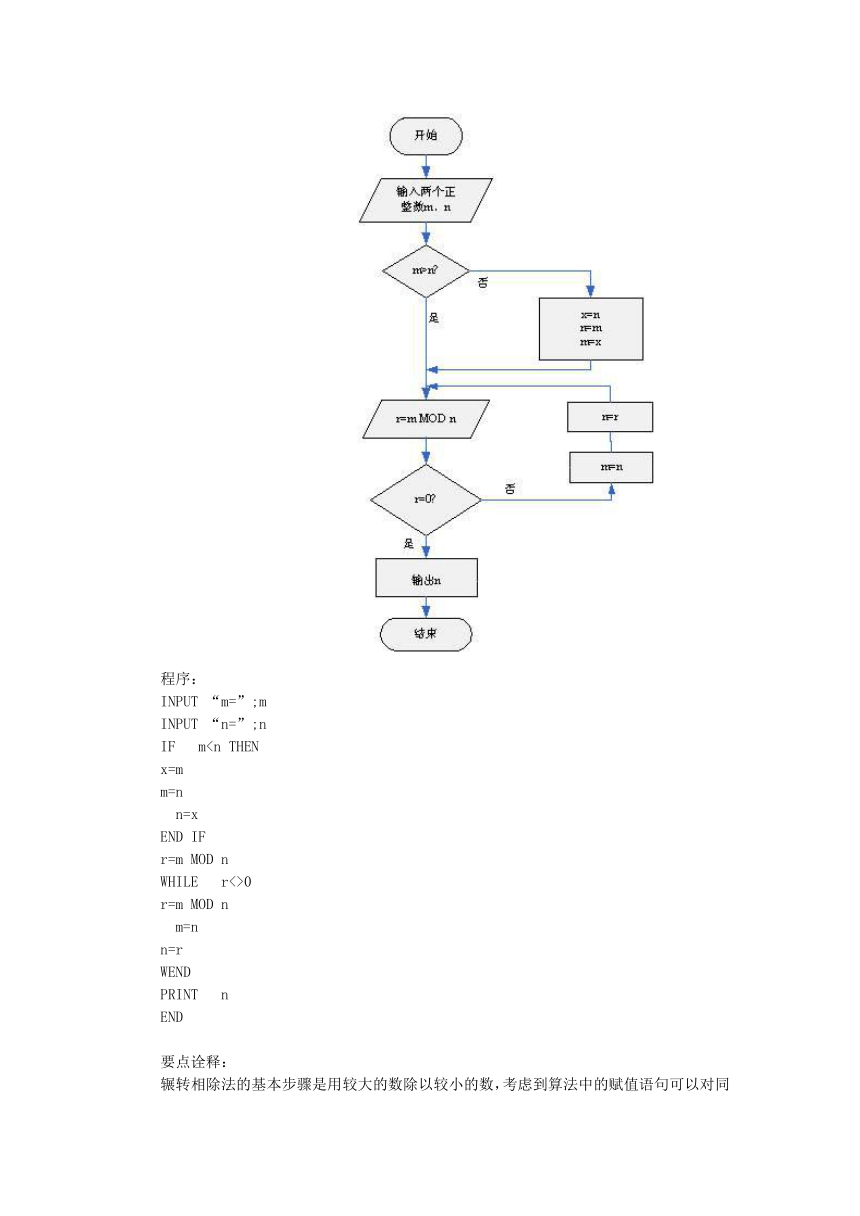
用辗转相除法求最大公约数的程序框图为:
程序:
INPUT “m=”;m
INPUT “n=”;n
IF m x=m
m=n
n=x
END IF
r=m MOD n
WHILE r<>0
r=m MOD n
m=n
n=r
WEND
PRINT n
END
要点诠释:
辗转相除法的基本步骤是用较大的数除以较小的数,考虑到算法中的赋值语句可以对同一变量多次赋值,我们可以把较大的数用变量m表示,把较小的数用变量n表示,这样式子就是一个反复执行的步骤,因此可以用循环结构实现算法.
知识点二:更相减损术
我国早期也有解决求最大公约数问题的算法,就是更相减损术.
更相减损术求最大公约数的步骤如下:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.
翻译出来为:
第一步:任意给出两个正整数;判断它们是否都是偶数.若是,用2约简;若不是,执行第二步.
第二步:以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数.继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数.
理论依据:
由,得与有相同的公约数
更相减损术一般算法:
第一步,输入两个正整数;
第二步,如果,则执行,否则转到;
第三步,将的值赋予;
第四步,若,则把赋予,把赋予,否则把赋予,重新执行;
第五步,输出最大公约数.
程序:
INPUT “a=”,a
INPUT “b=”,b
WHILE a<>b
IF a>=b
a=a-b;
ELSE
b=b-a
WEND
END
PRINT b
或者
INPUT “请输入两个不相等的正整数”;a,b
i=0
WHILE a MOD 2=0 AND b MOD 2=0
a=a/2
b=b/2
i=i+1
WEND
DO
IF b t=a
a=b
b=t
END IF
c=a-b
a=b
b=c
LOOP UNTIL a=b
PRINT a^i
END
要点诠释:
用辗转相除法步骤较少,而更相减损术虽然有些步骤较长,但运算简单.
知识点三:秦九韶计算多项式的方法
令,则有,
其中.这样,我们便可由依次求出;
要点诠释:
显然,用秦九韶算法求n次多项式的值时只需要做n次乘法和n次加法运算
知识点四:进位制
进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值.可使用数字符号的个数称为基数,基数为n,即可称n进位制,简称n进制.现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数.
对于任何一个数,我们可以用不同的进位制来表示.比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的.
表示各种进位制数一般在数字右下脚加注来表示,如111001(2)表示二进制数,34(5)表示5进制数.
1.k进制转换为十进制的方法:
,把k进制数a转化为十进制数b的算法程序为:
INPUT “ a,k,n=”;a,k,n
i=1
b=0
WHILE i<=n
t=GET a[i]
b=b+t*k^(i-1)
i=i+1
WEND
PRINT b
END
2.十进制转化为k进制数b的步骤为:
第一步,将给定的十进制整数除以基数k,余数便是等值的k进制的最低位;
第二步,将上一步的商再除以基数k,余数便是等值的k进制数的次低位;
第三步,重复第二步,直到最后所得的商等于0为止,各次所得的余数,便是k进制各位的数,最后一次余数是最高位,即除k取余法.
要点诠释:
1、在k进制中,具有k个数字符号.如二进制有0,1两个数字.
2、在k进制中,由低位向高位是按“逢k进一”的规则进行计数.
3、非k进制数之间的转化一般应先转化成十进制,再将这个十进制数转化为另一种进制的数,有的也可以相互转化.
三、规律方法指导
辗转相除法是西方古代数学中的一个典型算法.更相减损术和秦九韶算法都是我国古代数学中的著名算法,而进位制算法是计算机科学中普遍使用的算法.这些算法案例不仅蕴涵着深刻的算法思想,而且也更能体现出算法的重要性和有效性.因此,要切实理解算法案例的内容及具体算法的关键步骤.
一、目标认知
学习目标:
1.理解辗转相除法与更相减损术中蕴含的数学原理,并能根据这些原理进行算法分析;
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序;
3.了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质;
4.了解各种进位制与十进制之间转换的规律,会利用各种进位制与十进制之间的联系进行各种进位制之间的转换.
重点:
1.理解辗转相除法与更相减损术求最大公约数的方法;
2.秦九韶算法的特点;
3.各进位制表示数的方法及各进位制之间的转换.
难点:
1.把辗转相除法与更相减损术的方法转换成程序框图与程序语言;
2.秦九韶算法的先进性理解;
3.除k去余法的理解以及各进位制之间转换的程序框图的设计.
二、知识要点梳理
知识点一:辗转相除法
也叫欧几里德算法,它是由欧几里德在公元前300年左右首先提出的.利用辗转相除法求最大公约数的步骤如下:
第一步:用较大的数m除以较小的数n得到一个商q0和一个余数r0;
第二步:若r0=0,则n为m,n的最大公约数;若r0≠0,则用除数n除以余数r0得到一个商q1和一个余数r1;
第三步:若r1=0,则r1为m,n的最大公约数;若r1≠0,则用除数r0除以余数r1得到一个商q2和一个余数r2;
……
依次计算直至rn=0,此时所得到的rn-1即为所求的最大公约数.
用辗转相除法求最大公约数的程序框图为:
程序:
INPUT “m=”;m
INPUT “n=”;n
IF m
m=n
n=x
END IF
r=m MOD n
WHILE r<>0
r=m MOD n
m=n
n=r
WEND
PRINT n
END
要点诠释:
辗转相除法的基本步骤是用较大的数除以较小的数,考虑到算法中的赋值语句可以对同一变量多次赋值,我们可以把较大的数用变量m表示,把较小的数用变量n表示,这样式子就是一个反复执行的步骤,因此可以用循环结构实现算法.
知识点二:更相减损术
我国早期也有解决求最大公约数问题的算法,就是更相减损术.
更相减损术求最大公约数的步骤如下:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.
翻译出来为:
第一步:任意给出两个正整数;判断它们是否都是偶数.若是,用2约简;若不是,执行第二步.
第二步:以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数.继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数.
理论依据:
由,得与有相同的公约数
更相减损术一般算法:
第一步,输入两个正整数;
第二步,如果,则执行,否则转到;
第三步,将的值赋予;
第四步,若,则把赋予,把赋予,否则把赋予,重新执行;
第五步,输出最大公约数.
程序:
INPUT “a=”,a
INPUT “b=”,b
WHILE a<>b
IF a>=b
a=a-b;
ELSE
b=b-a
WEND
END
PRINT b
或者
INPUT “请输入两个不相等的正整数”;a,b
i=0
WHILE a MOD 2=0 AND b MOD 2=0
a=a/2
b=b/2
i=i+1
WEND
DO
IF b t=a
a=b
b=t
END IF
c=a-b
a=b
b=c
LOOP UNTIL a=b
PRINT a^i
END
要点诠释:
用辗转相除法步骤较少,而更相减损术虽然有些步骤较长,但运算简单.
知识点三:秦九韶计算多项式的方法
令,则有,
其中.这样,我们便可由依次求出;
要点诠释:
显然,用秦九韶算法求n次多项式的值时只需要做n次乘法和n次加法运算
知识点四:进位制
进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值.可使用数字符号的个数称为基数,基数为n,即可称n进位制,简称n进制.现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数.
对于任何一个数,我们可以用不同的进位制来表示.比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的.
表示各种进位制数一般在数字右下脚加注来表示,如111001(2)表示二进制数,34(5)表示5进制数.
1.k进制转换为十进制的方法:
,把k进制数a转化为十进制数b的算法程序为:
INPUT “ a,k,n=”;a,k,n
i=1
b=0
WHILE i<=n
t=GET a[i]
b=b+t*k^(i-1)
i=i+1
WEND
PRINT b
END
2.十进制转化为k进制数b的步骤为:
第一步,将给定的十进制整数除以基数k,余数便是等值的k进制的最低位;
第二步,将上一步的商再除以基数k,余数便是等值的k进制数的次低位;
第三步,重复第二步,直到最后所得的商等于0为止,各次所得的余数,便是k进制各位的数,最后一次余数是最高位,即除k取余法.
要点诠释:
1、在k进制中,具有k个数字符号.如二进制有0,1两个数字.
2、在k进制中,由低位向高位是按“逢k进一”的规则进行计数.
3、非k进制数之间的转化一般应先转化成十进制,再将这个十进制数转化为另一种进制的数,有的也可以相互转化.
三、规律方法指导
辗转相除法是西方古代数学中的一个典型算法.更相减损术和秦九韶算法都是我国古代数学中的著名算法,而进位制算法是计算机科学中普遍使用的算法.这些算法案例不仅蕴涵着深刻的算法思想,而且也更能体现出算法的重要性和有效性.因此,要切实理解算法案例的内容及具体算法的关键步骤.
