2023-2024学年初中数学湘教版七年级下册第6章 数据的分析 复习课 学案 (含答案)
文档属性
| 名称 | 2023-2024学年初中数学湘教版七年级下册第6章 数据的分析 复习课 学案 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 153.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 13:09:04 | ||
图片预览



文档简介
第6章 数据的分析 复习课
复习目标
1.说出算术平均数、权数、加权平均数、中位数、众数和方差的概念.
2.会求一组数据的算术平均数、加权平均数、中位数、众数和方差.
3.概述平均数、中位数、众数、方差的差别,初步感受它们在不同情境中的应用.
4.通过解决身边的实际问题,让学生初步认识数学与人类生活的密切联系,以及对人类历史发展的作用.
◎重点:1.说出算术平均数、加权平均数、中位数、众数和方差的概念.
2.会求一组数据的算术平均数、加权平均数、中位数、众数和方差.
预习导学
体系建构
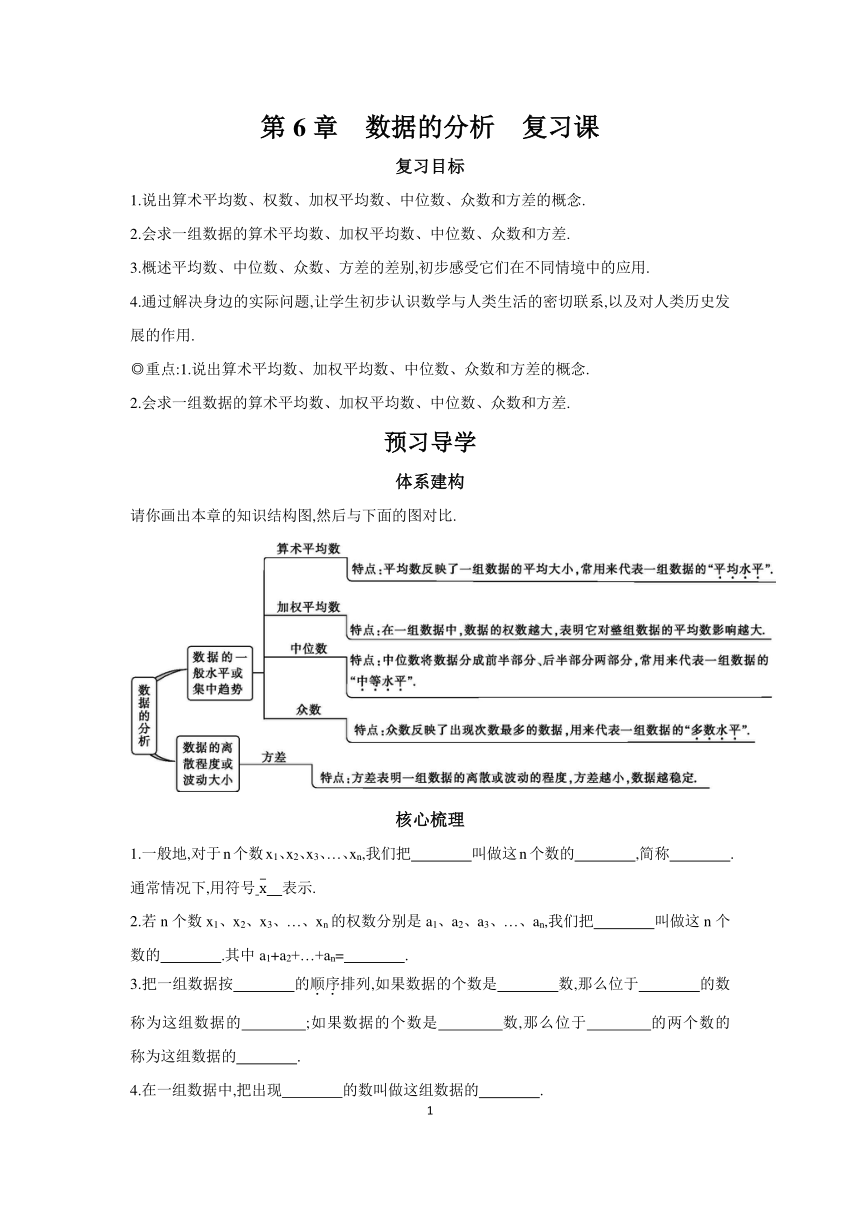
请你画出本章的知识结构图,然后与下面的图对比.
核心梳理
1.一般地,对于n个数x1、x2、x3、…、xn,我们把 叫做这n个数的 ,简称 .通常情况下,用符号 表示.
2.若n个数x1、x2、x3、…、xn的权数分别是a1、a2、a3、…、an,我们把 叫做这n个数的 .其中a1+a2+…+an= .
3.把一组数据按 的顺序排列,如果数据的个数是 数,那么位于 的数称为这组数据的 ;如果数据的个数是 数,那么位于 的两个数的 称为这组数据的 .
4.在一组数据中,把出现 的数叫做这组数据的 .
5.一组数据为x1、x2、x3、…、xn,各数与平均数之差的平方的平均值,叫做这组数据的 ,记做s2,即s2= .一般地,一组数据的方差越小,说明这组数据的 或 的程度就越小,这组数据也就越 .
【答案】1. 算术平均数 平均数
2.x1a1+x2a2+…+xnan 加权平均数 1
3.从小到大 奇 中间 中位数 偶 中间 平均数
中位数
4.次数最多 众数
5.方差 [(x1-)2+(x2-)2+…+(xn-)2] 离散 波动 稳定
合作探究
专题一 平均数与加权平均数
1.一组数据-4,5,1,3,4,3,2的算术平均数是 ( )
A.-2 B.-1 C.1 D.2
2.某一组数据由-4,2,5,0这4个不同的数组成,且它们的权数统计如下:
数据 -4 2 5 0
权数 0.4 0.2 0.3
则数0的权数是 ( )
A.0.1 B.0.2 C.0.3 D.0.4
【答案】1.D 2.A
专题二 中位数
3.一组数据3,3,2,2,2,5,5,5,5的中位数是 ( )
A.2 B.3 C.4 D.5
4.某公司10名职工5月份的工资统计如下:
工资/元 3000 3400 3600 4000
人数/人 2 3 1 4
则该公司10名职工5月份工资的中位数是 ( )
A.3200 B.3400
C.3500 D.3600
5.一组数据1,2,m,6,5,3的平均数是4,求这组数据的中位数.
【答案】3.B 4.C
5.解:由题意可知,(1+2+m+6+5+3)÷6=4,解得m=7,所以这一组数据为:1,2,7,6,5,3.将这一组数据按从小到大的顺序排列:1,2,3,5,6,7.这组数据一共有6个数据,所以这组数据的中位数为(3+5)÷2=4
专题三 众数
6.在一组数据3,3,5,2,5,4,2,3,4中,众数是 ( )
A.2 B.3 C.4 D.5
7.为响应建设“书香校园”的号召,某校随机调查了50名学生平均每天的阅读时间,得到如下结果:每天阅读0.5小时5人,每天阅读1小时18人,每天阅读1.5小时8人,其余的每天阅读2小时.则本次调查中阅读时间的众数是 .
8.已知一组数据:3,0,1,2,m,0,2,4的众数是0,求m的值.
【答案】6.B
7.2
8.解:因为3,0,1,2,m,0,2,4的众数是0,根据众数的定义,0出现的次数一定最多,又2已经出现了2次,所以0出现的次数必多于2次,而在给定的数据中0已经出现了2次,所以m的值是0.
专题四 中位数和众数
9.某班10名学生的校服尺寸与对应人数统计如下:
尺寸/cm 150 155 160 165 170
学生人数/人 1 4 2 1 2
求这10名学生校服尺寸的众数和中位数.
10.在某中学举行的“中国梦·校园好声音”歌唱比赛中,由于登分人员失误,记录时漏掉了一位同学的比赛成绩,结果统计如下:
编号 ① ② ③ ④ ⑤ ⑥ ⑦
得分 91 93 95 94 93 95
若这组数据的众数只有一个,求这组数据的中位数.
【答案】9.解:由表格可知,这10名学生校服尺寸的众数是155;
将这10名学生校服尺寸按从小到大的顺序排列:150,155,155,155,155,160,160,165,170,170.这组数据一共有10个数据,所以这组数据的中位数为(155+160)÷2=157.5.
10.解:因为这组数据的众数只有一个,所以这组数据的众数只能是93或95,所以这一组数据存在以下两种可能:①若这组数据的众数是93,则这组数据为91、93、95、94、93、93、95,将这组数据从小到大排列是91、93、93、93、94、95、95,所以这组数据的中位数是93;②若这组数据的众数是95,则这组数据为91、93、95、94、95、93、95,将这组数据从小到大排列是91,93,93,94,95,95,95,所以这组数据的中位数是94.
专题五 方差
11.某体校要从四名射击选手中选拔一名参加省体育运动会,经选拔获得如下数据:
队员 甲 乙 丙 丁
平均成绩 8.3 8.7 8.6 8.6
方差 1.0 1.1 3 1.4
为了获得最好成绩,如果你是教练,你的选择是 ( )
A.甲 B.乙 C.丙 D.丁
12.已知一组数据3,2,5,1,4,求这组数据的方差.
方法归纳交流 一组数据的 ,这组数据的 或 的程度就越小,当然也就越 .
13.甲、乙两台机床生产同种零件,10天出的次品数量分别是:
甲:5、6、5、7、7、5、8、6、7、9.
乙:7、8、6、7、5、7、6、6、7、6.
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好.
【答案】11.B
12.解:这组数据的平均数是=×(3+2+5+1+4)=3,所以这组数据的方差是s2=×[(3-3)2+(2-3)2+(5-3)2+(1-3)2+(4-3)2]=2.
方法归纳交流 方差越小 离散 波动 稳定
13.解:由题意可知,=×(5×3+6×2+7×3+8+9)=6.5,=×(7×4+8+6×4+5)=6.5,=×[(5-6.5)2×3+(6-6.5)2×2+(7-6.5)2×3+(8-6.5)2+(9-6.5)2]=1.65,=×[(7-6.5)2×4+(8-6.5)2+(6-6.5)2×4+(5-6.5)2]=0.65,
因为﹥,所以乙机床性能较好.
专题六 平均数、中位数和众数
14.某校生物兴趣小组20位学生在实验操作中的得分情况如下表:
得分/分 7 8 10 9
人数/人 6 4 3 7
求这组数据的平均数、众数、中位数.
【答案】14.解:由题意可知,这组数据的众数是9;将这一组数据按从小到大的顺序排列,排在第10、11位的数分别是8和9,所以这一组数据的中位数是(8+9)÷2=8.5,这一组数据的平均数是=×(7×6+8×4+10×3+9×7)=8.35.
2
复习目标
1.说出算术平均数、权数、加权平均数、中位数、众数和方差的概念.
2.会求一组数据的算术平均数、加权平均数、中位数、众数和方差.
3.概述平均数、中位数、众数、方差的差别,初步感受它们在不同情境中的应用.
4.通过解决身边的实际问题,让学生初步认识数学与人类生活的密切联系,以及对人类历史发展的作用.
◎重点:1.说出算术平均数、加权平均数、中位数、众数和方差的概念.
2.会求一组数据的算术平均数、加权平均数、中位数、众数和方差.
预习导学
体系建构
请你画出本章的知识结构图,然后与下面的图对比.
核心梳理
1.一般地,对于n个数x1、x2、x3、…、xn,我们把 叫做这n个数的 ,简称 .通常情况下,用符号 表示.
2.若n个数x1、x2、x3、…、xn的权数分别是a1、a2、a3、…、an,我们把 叫做这n个数的 .其中a1+a2+…+an= .
3.把一组数据按 的顺序排列,如果数据的个数是 数,那么位于 的数称为这组数据的 ;如果数据的个数是 数,那么位于 的两个数的 称为这组数据的 .
4.在一组数据中,把出现 的数叫做这组数据的 .
5.一组数据为x1、x2、x3、…、xn,各数与平均数之差的平方的平均值,叫做这组数据的 ,记做s2,即s2= .一般地,一组数据的方差越小,说明这组数据的 或 的程度就越小,这组数据也就越 .
【答案】1. 算术平均数 平均数
2.x1a1+x2a2+…+xnan 加权平均数 1
3.从小到大 奇 中间 中位数 偶 中间 平均数
中位数
4.次数最多 众数
5.方差 [(x1-)2+(x2-)2+…+(xn-)2] 离散 波动 稳定
合作探究
专题一 平均数与加权平均数
1.一组数据-4,5,1,3,4,3,2的算术平均数是 ( )
A.-2 B.-1 C.1 D.2
2.某一组数据由-4,2,5,0这4个不同的数组成,且它们的权数统计如下:
数据 -4 2 5 0
权数 0.4 0.2 0.3
则数0的权数是 ( )
A.0.1 B.0.2 C.0.3 D.0.4
【答案】1.D 2.A
专题二 中位数
3.一组数据3,3,2,2,2,5,5,5,5的中位数是 ( )
A.2 B.3 C.4 D.5
4.某公司10名职工5月份的工资统计如下:
工资/元 3000 3400 3600 4000
人数/人 2 3 1 4
则该公司10名职工5月份工资的中位数是 ( )
A.3200 B.3400
C.3500 D.3600
5.一组数据1,2,m,6,5,3的平均数是4,求这组数据的中位数.
【答案】3.B 4.C
5.解:由题意可知,(1+2+m+6+5+3)÷6=4,解得m=7,所以这一组数据为:1,2,7,6,5,3.将这一组数据按从小到大的顺序排列:1,2,3,5,6,7.这组数据一共有6个数据,所以这组数据的中位数为(3+5)÷2=4
专题三 众数
6.在一组数据3,3,5,2,5,4,2,3,4中,众数是 ( )
A.2 B.3 C.4 D.5
7.为响应建设“书香校园”的号召,某校随机调查了50名学生平均每天的阅读时间,得到如下结果:每天阅读0.5小时5人,每天阅读1小时18人,每天阅读1.5小时8人,其余的每天阅读2小时.则本次调查中阅读时间的众数是 .
8.已知一组数据:3,0,1,2,m,0,2,4的众数是0,求m的值.
【答案】6.B
7.2
8.解:因为3,0,1,2,m,0,2,4的众数是0,根据众数的定义,0出现的次数一定最多,又2已经出现了2次,所以0出现的次数必多于2次,而在给定的数据中0已经出现了2次,所以m的值是0.
专题四 中位数和众数
9.某班10名学生的校服尺寸与对应人数统计如下:
尺寸/cm 150 155 160 165 170
学生人数/人 1 4 2 1 2
求这10名学生校服尺寸的众数和中位数.
10.在某中学举行的“中国梦·校园好声音”歌唱比赛中,由于登分人员失误,记录时漏掉了一位同学的比赛成绩,结果统计如下:
编号 ① ② ③ ④ ⑤ ⑥ ⑦
得分 91 93 95 94 93 95
若这组数据的众数只有一个,求这组数据的中位数.
【答案】9.解:由表格可知,这10名学生校服尺寸的众数是155;
将这10名学生校服尺寸按从小到大的顺序排列:150,155,155,155,155,160,160,165,170,170.这组数据一共有10个数据,所以这组数据的中位数为(155+160)÷2=157.5.
10.解:因为这组数据的众数只有一个,所以这组数据的众数只能是93或95,所以这一组数据存在以下两种可能:①若这组数据的众数是93,则这组数据为91、93、95、94、93、93、95,将这组数据从小到大排列是91、93、93、93、94、95、95,所以这组数据的中位数是93;②若这组数据的众数是95,则这组数据为91、93、95、94、95、93、95,将这组数据从小到大排列是91,93,93,94,95,95,95,所以这组数据的中位数是94.
专题五 方差
11.某体校要从四名射击选手中选拔一名参加省体育运动会,经选拔获得如下数据:
队员 甲 乙 丙 丁
平均成绩 8.3 8.7 8.6 8.6
方差 1.0 1.1 3 1.4
为了获得最好成绩,如果你是教练,你的选择是 ( )
A.甲 B.乙 C.丙 D.丁
12.已知一组数据3,2,5,1,4,求这组数据的方差.
方法归纳交流 一组数据的 ,这组数据的 或 的程度就越小,当然也就越 .
13.甲、乙两台机床生产同种零件,10天出的次品数量分别是:
甲:5、6、5、7、7、5、8、6、7、9.
乙:7、8、6、7、5、7、6、6、7、6.
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好.
【答案】11.B
12.解:这组数据的平均数是=×(3+2+5+1+4)=3,所以这组数据的方差是s2=×[(3-3)2+(2-3)2+(5-3)2+(1-3)2+(4-3)2]=2.
方法归纳交流 方差越小 离散 波动 稳定
13.解:由题意可知,=×(5×3+6×2+7×3+8+9)=6.5,=×(7×4+8+6×4+5)=6.5,=×[(5-6.5)2×3+(6-6.5)2×2+(7-6.5)2×3+(8-6.5)2+(9-6.5)2]=1.65,=×[(7-6.5)2×4+(8-6.5)2+(6-6.5)2×4+(5-6.5)2]=0.65,
因为﹥,所以乙机床性能较好.
专题六 平均数、中位数和众数
14.某校生物兴趣小组20位学生在实验操作中的得分情况如下表:
得分/分 7 8 10 9
人数/人 6 4 3 7
求这组数据的平均数、众数、中位数.
【答案】14.解:由题意可知,这组数据的众数是9;将这一组数据按从小到大的顺序排列,排在第10、11位的数分别是8和9,所以这一组数据的中位数是(8+9)÷2=8.5,这一组数据的平均数是=×(7×6+8×4+10×3+9×7)=8.35.
2
