1.4 整式的乘法(第3课时) 课件(共20张PPT)
文档属性
| 名称 | 1.4 整式的乘法(第3课时) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-28 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
北师大七下数学
同步精品课件
北师大版七年级下册
2024春北师大版七下数学精品课件
第一章 整式的乘除
1.4 整式的乘法
第3课时
1.理解并经历探索多项式乘多项式法则的过程,熟练应用多项式乘多项式的法则解决问题.(重点)
2.培养独立思考、主动探索的习惯和初步解决问题的能力.
学习目标
回顾 & 思考
1.单项式与单项式相乘
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
2.单项式与多项式相乘
单项式与多项式相乘,就是根据乘法分配律用单项式去乘多项式的每一项,再把所得的积相加.
3.进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.
情景引入
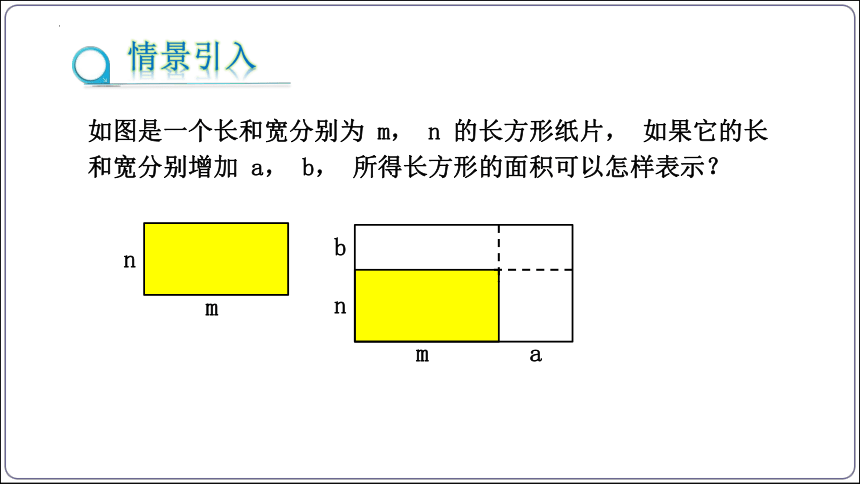
如图是一个长和宽分别为 m, n 的长方形纸片, 如果它的长和宽分别增加 a, b, 所得长方形的面积可以怎样表示?
m
n
m
n
a
b
探索&交流
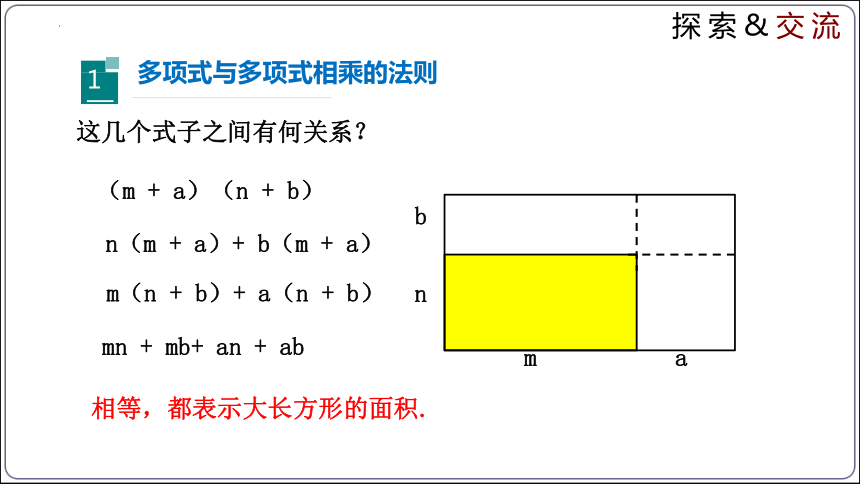
多项式与多项式相乘的法则
1—
(m + a)(n + b)
n(m + a)+ b(m + a)
m(n + b)+ a(n + b)
mn + mb+ an + ab
m
n
a
b
这几个式子之间有何关系?
相等,都表示大长方形的面积.
因为它们表示的都是同一块绿地的面积,所以可以得到结论:
( ) ( ) =
=
把(m+a)或者(n+b)看成一个整体,利用乘法分配律,用单项式乘多项项式理解公式展开
探索&交流
你能类比单项式与多项式相乘的法则,叙述多项式与多项式相乘的法则吗?
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘以多项式
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
议一议
探索&交流
典例精析
例1.计算:
(1) (1-x) (0.6-x); (2) (2x + y) (x-y) .
解:(1) (1-x) (0.6-x)=1×0.6-1× x + x×0.6 + x·x
=0.6-x-0.6x+ x2
=0.6-1.6x+ x2 ;
(2) (2x + y) (x-y)
=2x·x-2x·y + y·x-y·y
=2x2-2xy+xy-y2 =2x2-xy-y2.
解:原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
注意:(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式(是同类项的要合并).
(3) (x+y)(x2-xy+y2).
典例精析
例2.计算:(1)(a-b)(a2+ab+b2);
(2)(x2+x+1)(x2-x+1).
(1)原式=a·a2+a·ab+a·b2+(-b)·a2+(-b)·ab+(-b)·b2
=a3+a2b+ab2-a2b-ab2-b3 =a3-b3;
(2)原式=x2·x2+x2·(-x)+x2·1+x·x2+x·(-x)+x·1
+x2-x+1
=x4-x3+x2+x3-x2+x+x2-x+1 =x4+x2+1.
做一做
探索&交流
(x + 2)(x + 3)= x2 +____x +____
(x – 2)(x + 3)= x2 +____x +____
(x + 2)(x – 3)= x2 +____x +____
(x – 2)(x – 3)= x2 +____x +____
5
观察上面四个等式,你能发现什么规律?
6
1
–6
–1
–6
–5
6
(x+a)(x+b)= x2+(a+b)x+ab
多项式乘以多项式时,应注意以下几点:
(1)相乘时,按一定的顺序进行,必须做到不重不漏;
(2)多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数应等于原多项式的项数之积;
(3)相乘后,若有同类项应该合并.
(x+a)(x+b)= x2+(a+b)x+ab
探索&交流
典例精析
例3.若(x+2)(x-3)=x2+ax+b,求a2+ab的值.
解:因为(x+2)(x-3)=x2-3x+2x-6=x2-x-6,
所以x2-x-6=x2+ax+b.
因此a=-1,b=-6.
所以a2+ab=(-1)2+(-1)×(-6)=7.
随堂练习
练习&巩固
B
1.下列多项式相乘,结果为x2-4x-12的是 ( )
A.(x-4)(x+3) B.(x-6)(x+2)
C.(x-4)(x-3) D.(x+6)(x-2)
练习&巩固
B
2.若(x-1)(x+3)=x2+mx+n,那么m,n的值分别是( )
A.m=1,n=3 B.m=2,n=-3
C.m=4,n=5 D.m=-2,n=3
练习&巩固
C
3.如果(x+a)(x+b)的结果中不含x的一次项,那么a,b满足 ( )
A.a=b B.a=0
C.a=-b D.b=0
小结&反思
1.多项式与多项式相乘时要按一定的顺序进行,做到不重不漏.
2.多项式与多项式相乘时每一项都包含符号,在计算时先准确地确定积的符号.
3.多项式与多项式相乘的结果若含有同类项,必须合并同类项.在合并同类项之前的项数应该等于两个多项式的项数之积.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
北师大七下数学
同步精品课件
北师大版七年级下册
2024春北师大版七下数学精品课件
第一章 整式的乘除
1.4 整式的乘法
第3课时
1.理解并经历探索多项式乘多项式法则的过程,熟练应用多项式乘多项式的法则解决问题.(重点)
2.培养独立思考、主动探索的习惯和初步解决问题的能力.
学习目标
回顾 & 思考
1.单项式与单项式相乘
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
2.单项式与多项式相乘
单项式与多项式相乘,就是根据乘法分配律用单项式去乘多项式的每一项,再把所得的积相加.
3.进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.
情景引入
如图是一个长和宽分别为 m, n 的长方形纸片, 如果它的长和宽分别增加 a, b, 所得长方形的面积可以怎样表示?
m
n
m
n
a
b
探索&交流
多项式与多项式相乘的法则
1—
(m + a)(n + b)
n(m + a)+ b(m + a)
m(n + b)+ a(n + b)
mn + mb+ an + ab
m
n
a
b
这几个式子之间有何关系?
相等,都表示大长方形的面积.
因为它们表示的都是同一块绿地的面积,所以可以得到结论:
( ) ( ) =
=
把(m+a)或者(n+b)看成一个整体,利用乘法分配律,用单项式乘多项项式理解公式展开
探索&交流
你能类比单项式与多项式相乘的法则,叙述多项式与多项式相乘的法则吗?
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘以多项式
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
议一议
探索&交流
典例精析
例1.计算:
(1) (1-x) (0.6-x); (2) (2x + y) (x-y) .
解:(1) (1-x) (0.6-x)=1×0.6-1× x + x×0.6 + x·x
=0.6-x-0.6x+ x2
=0.6-1.6x+ x2 ;
(2) (2x + y) (x-y)
=2x·x-2x·y + y·x-y·y
=2x2-2xy+xy-y2 =2x2-xy-y2.
解:原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
注意:(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式(是同类项的要合并).
(3) (x+y)(x2-xy+y2).
典例精析
例2.计算:(1)(a-b)(a2+ab+b2);
(2)(x2+x+1)(x2-x+1).
(1)原式=a·a2+a·ab+a·b2+(-b)·a2+(-b)·ab+(-b)·b2
=a3+a2b+ab2-a2b-ab2-b3 =a3-b3;
(2)原式=x2·x2+x2·(-x)+x2·1+x·x2+x·(-x)+x·1
+x2-x+1
=x4-x3+x2+x3-x2+x+x2-x+1 =x4+x2+1.
做一做
探索&交流
(x + 2)(x + 3)= x2 +____x +____
(x – 2)(x + 3)= x2 +____x +____
(x + 2)(x – 3)= x2 +____x +____
(x – 2)(x – 3)= x2 +____x +____
5
观察上面四个等式,你能发现什么规律?
6
1
–6
–1
–6
–5
6
(x+a)(x+b)= x2+(a+b)x+ab
多项式乘以多项式时,应注意以下几点:
(1)相乘时,按一定的顺序进行,必须做到不重不漏;
(2)多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数应等于原多项式的项数之积;
(3)相乘后,若有同类项应该合并.
(x+a)(x+b)= x2+(a+b)x+ab
探索&交流
典例精析
例3.若(x+2)(x-3)=x2+ax+b,求a2+ab的值.
解:因为(x+2)(x-3)=x2-3x+2x-6=x2-x-6,
所以x2-x-6=x2+ax+b.
因此a=-1,b=-6.
所以a2+ab=(-1)2+(-1)×(-6)=7.
随堂练习
练习&巩固
B
1.下列多项式相乘,结果为x2-4x-12的是 ( )
A.(x-4)(x+3) B.(x-6)(x+2)
C.(x-4)(x-3) D.(x+6)(x-2)
练习&巩固
B
2.若(x-1)(x+3)=x2+mx+n,那么m,n的值分别是( )
A.m=1,n=3 B.m=2,n=-3
C.m=4,n=5 D.m=-2,n=3
练习&巩固
C
3.如果(x+a)(x+b)的结果中不含x的一次项,那么a,b满足 ( )
A.a=b B.a=0
C.a=-b D.b=0
小结&反思
1.多项式与多项式相乘时要按一定的顺序进行,做到不重不漏.
2.多项式与多项式相乘时每一项都包含符号,在计算时先准确地确定积的符号.
3.多项式与多项式相乘的结果若含有同类项,必须合并同类项.在合并同类项之前的项数应该等于两个多项式的项数之积.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
