5.4 抛体运动的规律课件-2023-2024学年高一下学期物理人教版(2019)必修第二册(38张PPT)
文档属性
| 名称 | 5.4 抛体运动的规律课件-2023-2024学年高一下学期物理人教版(2019)必修第二册(38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-27 09:36:03 | ||
图片预览



文档简介
(共38张PPT)
第五章 抛体运动
5.4抛体运动的规律
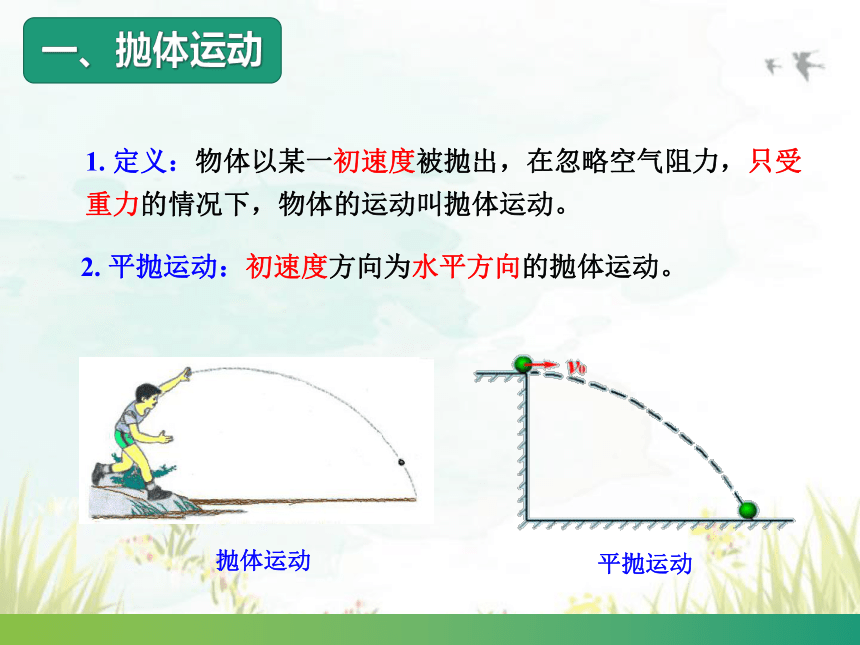
1. 定义:物体以某一初速度被抛出,在忽略空气阻力,只受重力的情况下,物体的运动叫抛体运动。
2. 平抛运动:初速度方向为水平方向的抛体运动。
平抛运动
抛体运动
一、抛体运动
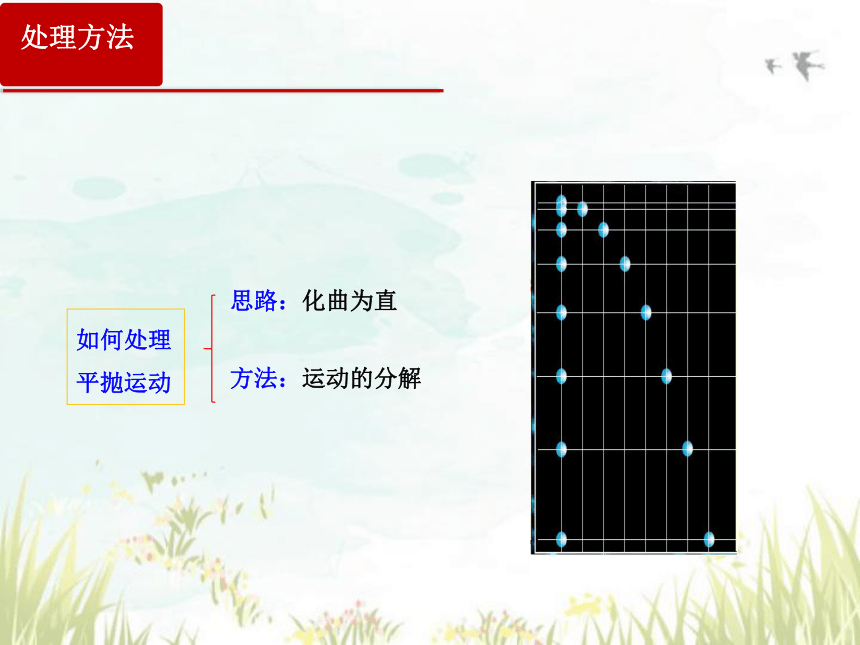
如何处理平抛运动
处理方法
思路:化曲为直
方法:运动的分解
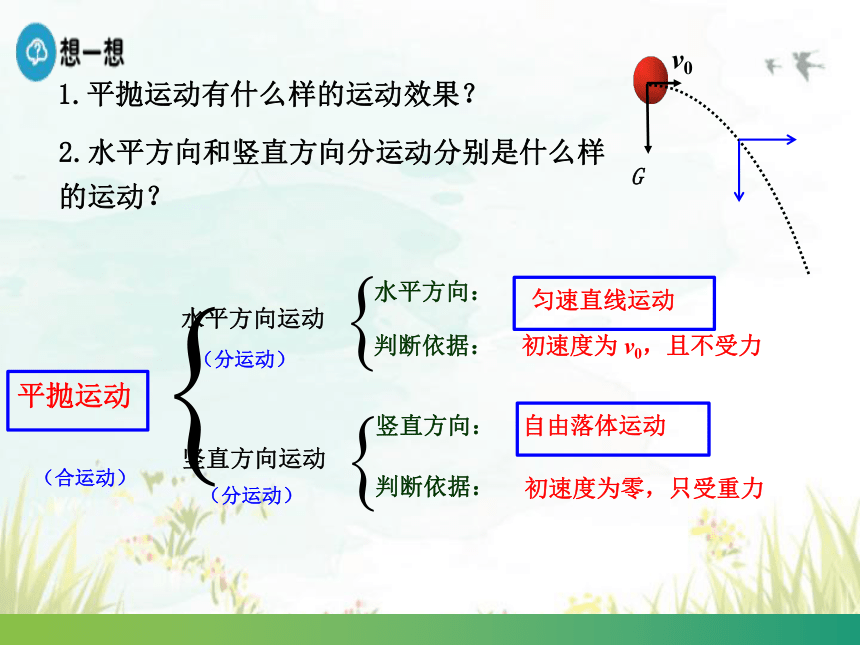
1.平抛运动有什么样的运动效果?
平抛运动
水平方向运动
竖直方向运动
2.水平方向和竖直方向分运动分别是什么样的运动?
水平方向:
判断依据:
初速度为 v0,且不受力
匀速直线运动
竖直方向:
判断依据:
初速度为零,只受重力
自由落体运动
v0
G
(分运动)
(分运动)
(合运动)
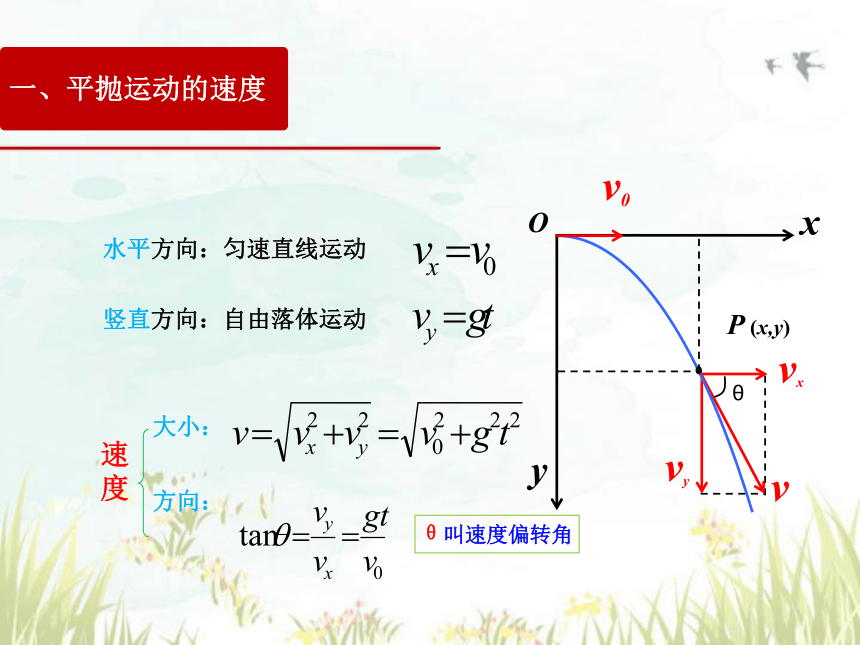
水平方向:匀速直线运动
竖直方向:自由落体运动
速
度
大小:
方向:
一、平抛运动的速度
θ
vx
vy
v
O
x
y
v0
P (x,y)
θ叫速度偏转角
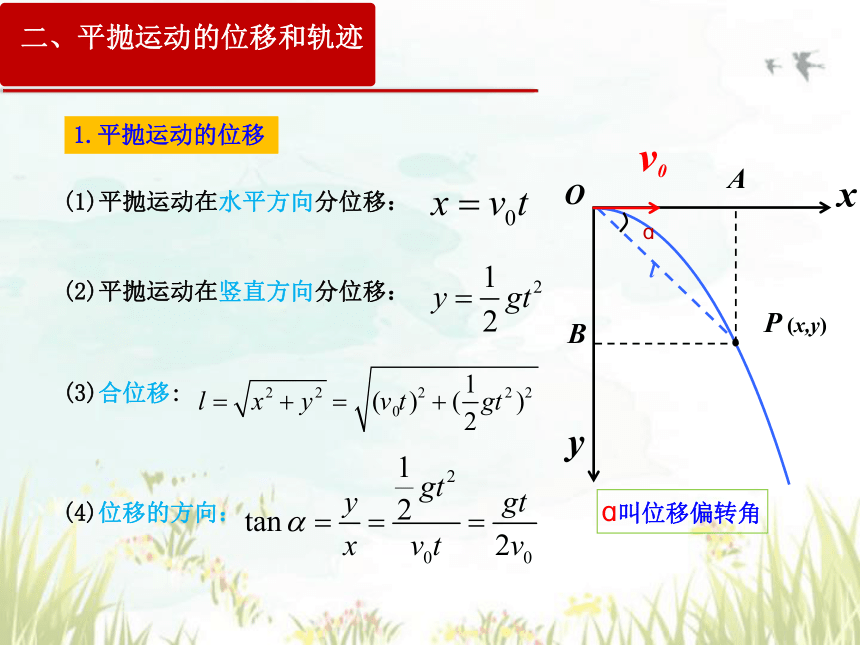
(4)位移的方向:
(2)平抛运动在竖直方向分位移:
(1)平抛运动在水平方向分位移:
(3)合位移:
1.平抛运动的位移
二、平抛运动的位移和轨迹
l
O
x
y
P (x,y)
B
A
v0
ɑ
ɑ叫位移偏转角
(3)结论:平抛运动的轨迹是一条抛物线。
(1)水平方向:匀速直线运动
(2)竖直方向:自由落体运动
消去 t 得:
2.平抛运动的轨迹
二、平抛运动的位移和轨迹
B
A
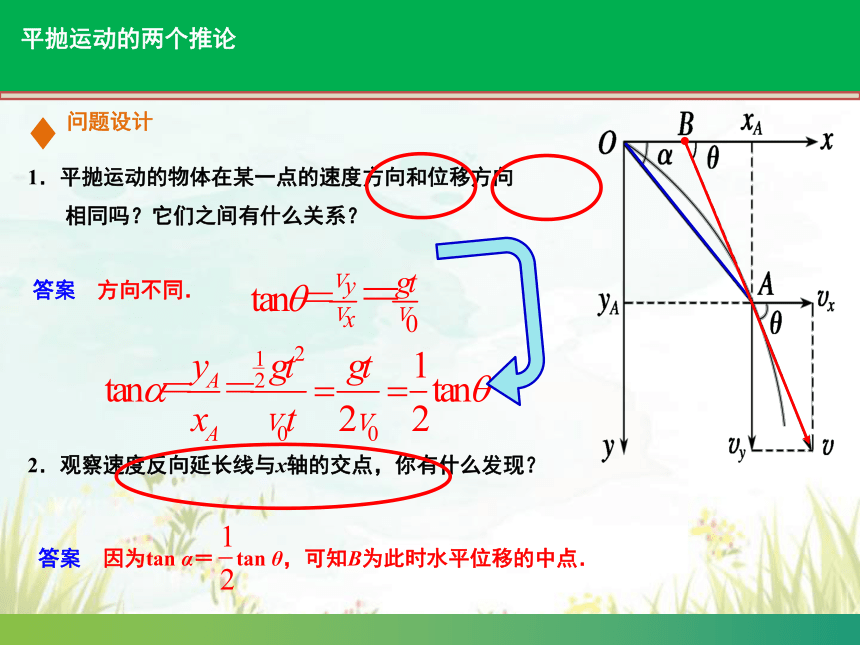
1.平抛运动的物体在某一点的速度方向和位移方向
相同吗?它们之间有什么关系?
问题设计
答案 方向不同.
平抛运动的两个推论
2.观察速度反向延长线与x轴的交点,你有什么发现?
答案 因为tan α= tan θ,可知B为此时水平位移的中点.
v
C
O
x
y
t
θ
vx
vy
α
x
y
竖直方向:
水平方向:
合位移:
合速度:
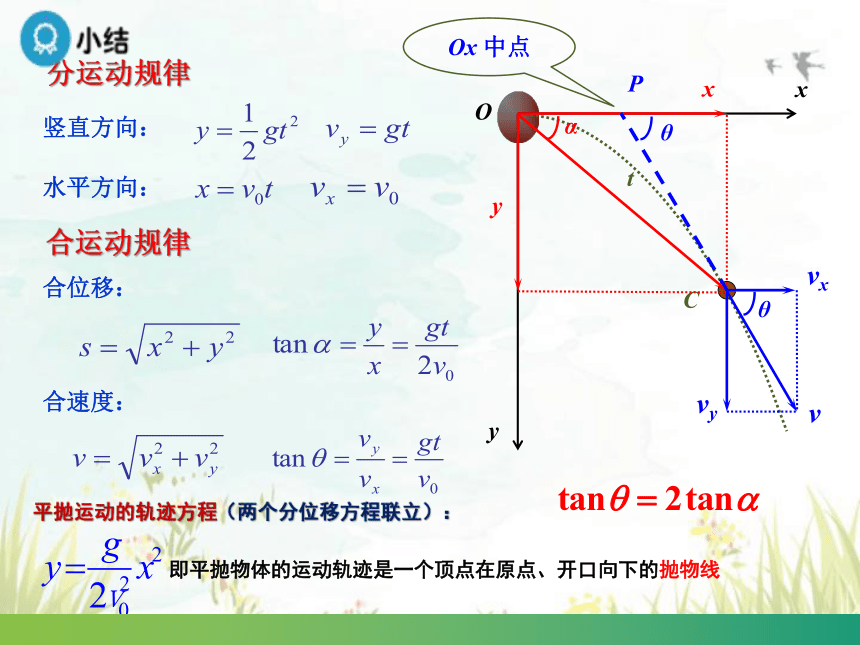
分运动规律
合运动规律
P
θ
Ox 中点
平抛运动的轨迹方程(两个分位移方程联立):
即平抛物体的运动轨迹是一个顶点在原点、开口向下的抛物线
平抛运动的理解
典例精析
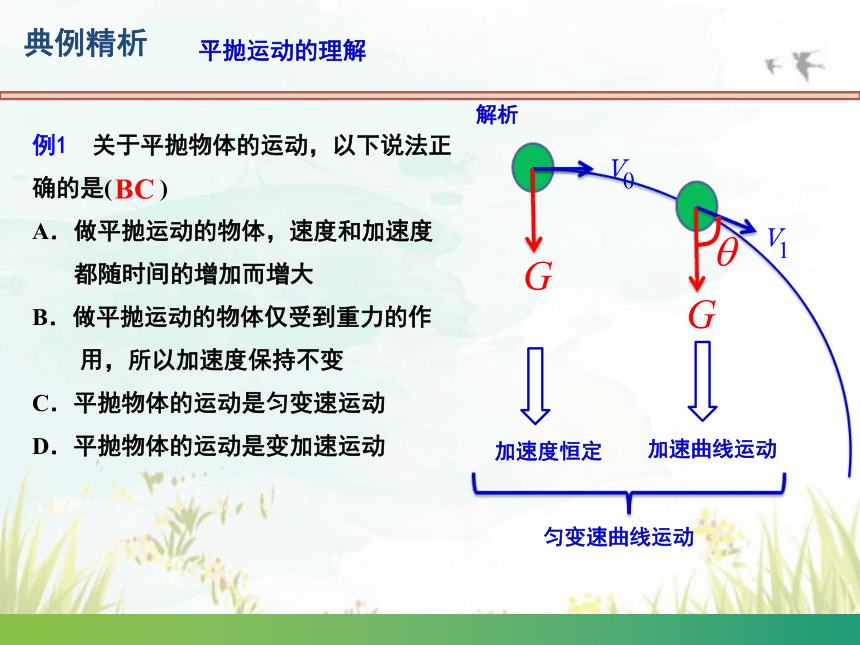
例1 关于平抛物体的运动,以下说法正确的是( )
A.做平抛运动的物体,速度和加速度
都随时间的增加而增大
B.做平抛运动的物体仅受到重力的作
用,所以加速度保持不变
C.平抛物体的运动是匀变速运动
D.平抛物体的运动是变加速运动
BC
加速度恒定
加速曲线运动
匀变速曲线运动
解析
例2. 将一个物体以 10 m/s 的速度从 5 m 的高度水平抛出,落地时它的速度方向与地面的夹角 θ 是多少 (不计空气阻力,取 g = 10 m/s2)
解析:落地时,物体水平分速度:
vx= v0 = 10 m/s
vy 根据匀变速运动的规律,竖直方向分速度 vy 满足以下关系:
vy2 0 = 2gh,由此解出:vy= 10 m/s
tan θ = vy/vx = 1
物体落地时速度与地面的夹角是 45°
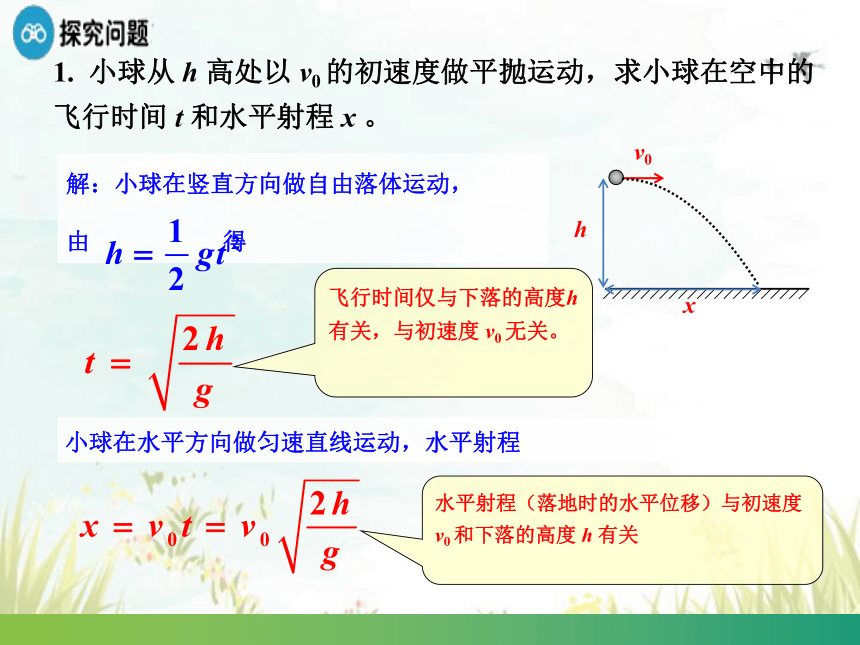
1. 小球从 h 高处以 v0 的初速度做平抛运动,求小球在空中的飞行时间 t 和水平射程 x 。
解:小球在竖直方向做自由落体运动,
由 得
小球在水平方向做匀速直线运动,水平射程
飞行时间仅与下落的高度h有关,与初速度 v0 无关。
水平射程(落地时的水平位移)与初速度 v0 和下落的高度 h 有关
x
v0
h
2. 小球从 h 高处以 v0 的初速度做平抛运动,求小球落地时速度 v 的大小。
x
v0
h
落体的速度 v 由初速度 v0 和下落高度 h 共同决定
v
vx
vy
1. 平抛运动在空中飞行时间:
与质量和初速度大小无关,只由高度 h 决定
2. 平抛运动的水平最大射程:
3. 落地速度
由初速度 v0 和下落高度 h 共同决定,与质量无关
由初速度 v0 和下落高度 h 共同决定,与质量无关
(1)理想化特点:平抛运动是一种理想化的模型,即把物体看成质点,抛出后只考虑重力作用,忽略空气阻力.
(2)匀变速特点:平抛运动的加速度恒定,即始终等于重力加速度.
(3)速度变化特点:任意两个相等的时间间隔内速度的变化相同,
Δv=gΔt,方向竖直向下,如下所示.
v0
gΔt
Δv=gΔt
Δv=gΔt
Δv=gΔt
2gΔt
3gΔt
平抛运动的三个特点
1. 概念:把物体以一定的初速度 v0 斜向上或斜向下抛出去,物体只在重力作用下所做的运动叫做斜抛运动。
2.斜抛运动的性质:由于斜抛运动的加速度是重力加速度,且与速度方向有夹角,因此,斜抛运动是匀变速曲线运动.
斜抛运动
x
水平方向初速度: Vox = Vo cos , ax = 0
竖直方向初速度: Voy = Vo sin , ay = g,方向向下
y
vox
voy
vo
射高H
射程S
水平方向:匀速直线运动
竖直方向:竖直上抛运动
斜上抛运动
位移:x=voxt= v0tcosθ
位移:
速度:vy=v0y-gt=v0sin θ-gt
速度:vx=v0x=v0cosθ
匀速直线运动
竖直上抛运动
X轴:
Y轴:
v0y
v0
x
v0x
y
0
v
vx
vy
合速度大小:
合速度方向:
合位移大小:
s
y
x
合位移方向:
分
解
斜抛运动的规律
平抛
课堂小结
斜抛
抛体运动的规律
思路:化曲为直
方法:运动的分解
水平方向:
竖直方向:
速度
位移
x=v0tcos
vx=v0cos
vy=v0sin - gt
【例1】. 如图所示,x 轴在水平地面内,y 轴沿竖直方向。图中画出了从 y 轴上沿 x 轴正向抛出的三个小球 a、b 和 c 的运动轨迹,其中 b 和 c 是从同一点抛出的。不计空气阻力,则( )
A. a 的飞行时间比 b 的长
B. b 和 c 的飞行时间相同
C. a 的水平速度比 b 的小
D. b 的初速度比 c 的大
BD
【例2】玩具轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A。已知A点高度为h=3.6m,山坡倾角为37°,g取10m/s2,由此可算出( )
A. 炸弹的飞行时间为0.8s
B. 轰炸机的飞行速度是8m/s
C. 轰炸机的飞行高度为5.2m
D. 炸弹飞行的水平位移为3.6m
A
【例3】 (2021·浙江高一月考)如图所示,从倾角为θ的足够长的斜面顶端P以速度v抛出一个小球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变为2v,则( )
A.小球的水平位移和竖直位移之比变为原来的2倍
B.夹角α将变原来的2倍
C.PQ间距一定为原来问距的2倍
D.空中的运动时间变为原来的2倍
D
1.某同学在某一水平直线上相同高度的A、B、C三个位置先后斜上抛出三个小球,结果三个小球都能够垂直击中墙壁的同一位置,设三次抛出的小球在空中飞行时间分别为t1、t2、t3,到达墙壁的速度分别为v1、v2、v3,不计空气阻力,则( )
A.t1>t2>t3 , v1>v2>v3
B.t1>t2>t3 , v1=v2=v3
C.t1=t2=t3 , v1>v2>v3
D.t1=t2=t3 , v1=v2=v3
A
C
B
C
题型1.多体平抛
2.如图所示,用6 m 长的轻绳将 A、B两球相连,两球相隔0.8 s先后从C点以4.5m/s的初速度水平抛出.那么,将A球抛出后经多长时间,A、B 间的轻绳刚好被拉直 (g=10m/s2)
【答案】1s
3.如图所示,一把玩具枪在同一高度以分别以速度2v和3v射出两颗子弹并击中竖直墙壁的A和B两点,下列说法正确的是( )
A.子弹击中A、B的运动时间之比为1:1
B.子弹击中A、B的运动时间之比为3:2
C.子弹击中A、B的竖直位移之比为2 :1
D.子弹击中A、B的竖直位移之比为9 :4
BD
题型2.各种落地方式的平抛
平抛时间由下落高度决定,不是离地高度
4.如图所示,从倾角为θ的足够长的斜面顶端P以速度v抛出一个小球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变为2v,则( )
A.小球的水平位移和竖直位移之比变为原来的2倍
B.夹角α将变原来的2倍
C.PQ间距一定为原来间距的2倍
D.空中的运动时间变为原来的2倍
D
顺抛落地,“三角”一定
斜面上的顺抛
5.如图所示,小球以v0正对倾角为θ的斜面水平抛出,若小球垂直撞击斜面,则飞行时间t为(重力加速度为g)
( )
A.v0tanθ B.
C. D.
C
垂直落地,“一角”一定
斜面上垂直对抛1
6.如图所示,小球以v0正对倾角为θ的斜面水平抛出,若小球到达斜面的位移最小,则飞行时间t为(重力加速度为g)( )
A.v0tanθ B.
C. D.
D
垂直落地,“一角”一定
53
1.如图所示,水平地面上有一斜面山坡,山坡倾角为53 ,高为80m,一小球
从山坡顶端水平抛出,不计空气阻力,(重力加速度为g=10m/s2)求
(1)若初速度为20m/s时,求水平位移多大?
(2)若v0=12m/s,小球离斜面最远时的运动时间和最远距离?
【答案】(1)80m (2) 1.6s ;7.68m
(1)方法:分解速度和加速度法
(2)规律:沿斜面方向匀加速,垂直斜面先匀减速后匀加速
(3)对称性特点:
离斜面最远点时间和回落到斜面的时间对称,t=v0tanθ/g.
沿斜面方向的位移大小_______
(4)极值和临界分析:
离斜面有最大距离L=__________________
恰好落在斜面上的速度临界值V=______
不对称
斜面上平抛的运动分解处理和极值
v0x
v0y
v0
g
gy
gx
v
vy
v0
7.(多选)如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环的半径为R。一小球从A沿AB方向以速度V水平抛出,不计空气阻力,则( )
A.V不同时,小球在空中运动时间可能相同
B.V合适时有可能垂直撞击BC之间圆环
C. 如果抛出点在A的正上方时,有可能垂直撞击BC之间圆环
D. 如果抛出点水平向右侧移时,有可能垂直撞击BC之间圆环。
A
C
B
ACD
球面上垂直抛
题型2.常见平抛时间的求值方法总结
(1)位移法:
已知水平位移: t=x/v0 如撞击竖直墙壁,
已知竖直位移: 如撞击水平地面,
(2)速度法:竖直分速度一定:t=vy/g:
顺抛撞击斜面: t=vy/g=2v0tanθ/g
对抛速度垂直斜面:t=vy/g=v0/gtanθ
对抛位移垂直斜面:t=vy/g=2v0/gtanθ
8.如图所示,质量相同的、两质点从同一点分别以相同的水平速度沿轴正方向抛出,在竖直平面内运动,落地点为p1;沿光滑斜面运动,落地点为p2。和在同一水平面内,不计空气阻力,则下列说法中正确的是( )
A.A、B的运动时间相同
B.A、B沿轴方向的位移相同
C.A、B落地时的速度大小相同
D.A、B落地时的速度不同
CD
题型3.类平抛问题
D
9.质量m=4kg的质点静止在光滑水平面上的直角坐标系的原点,先用沿x轴正方向的力F1=8N作用了2s,然后撤去F1;再用沿y轴正方向的力F2=24N作用了1s.则质点在这3s内的轨迹为( )
10.如图所示,有一倾角为30°的光滑斜面,斜面长L为10m,一小球从斜面顶端以10m/s的速度在斜面上沿水平方向抛出.(g取10 m/s )求∶
(1)小球沿斜面滑到底端时的水平位移x.
(2)小球到达斜面底端时的速度大小.
【答案】(1)20m ; (2) 14.1m/s
1.类平抛定义:
物体具有一定初速度,只受到和初速度垂直方向的恒力作用的运动方式
2.类平抛的规律
(1)初速度方向:匀速直线运动
(2)恒力方向:初速度为零的匀加速直线运动a=F合/m
3.和平抛的比较
(1)初速度方向是任意的,不一定是水平方向
(2)恒力大小任意,方向不一定是竖直向下,但一定和初速度垂直。
(3)平抛的推论也适用于类平抛
4.解题思路:
(1)求合力大小和方向,求加速度大小和方向
(2)确认初速度方向和加速度方向是否垂直
(3)沿初速度和加速度方向进行运动分解
(4)求解相关量
题型3.类平抛运动总结
(θ≠2α)
1.如图所示,乒乓球水平发球点在桌面的中心处,以不同速率,朝右侧以不同方向水平发射乒乓球,发球点高度为3h,球网高度为h,桌面长和宽分别为L1和L2,要成功发球,不计空气阻力,则乒乓球水平抛出的初速度的取值范围?
题型4、平抛运动中的临界极值问题
【例1】如图所示,窗子上、下沿间的高度H=1.6 m,墙的厚度d=0.4 m,某人在离墙壁L=1.4 m、距窗子上沿h=0.2 m处的P点,将可视为质点的小物体以速度v平行墙面方向水平抛出,小物体直接穿过窗口并落在水平地面上,g取10 m/s2.则v的取值范围是( )
A.v>7 m/s B.v<2.3 m/s
C.3 m/sC
C
2.障碍物平抛的速度临界问题总结
(1)作运动轨迹的速度渐进动态图
(2)确定临界状态对应的竖直位移一定时的最大最小水平位移
(3)求对应既定竖直位移对应的时间
(4)求最大最小水平位移的初速度,确定其范围。
第五章 抛体运动
5.4抛体运动的规律
1. 定义:物体以某一初速度被抛出,在忽略空气阻力,只受重力的情况下,物体的运动叫抛体运动。
2. 平抛运动:初速度方向为水平方向的抛体运动。
平抛运动
抛体运动
一、抛体运动
如何处理平抛运动
处理方法
思路:化曲为直
方法:运动的分解
1.平抛运动有什么样的运动效果?
平抛运动
水平方向运动
竖直方向运动
2.水平方向和竖直方向分运动分别是什么样的运动?
水平方向:
判断依据:
初速度为 v0,且不受力
匀速直线运动
竖直方向:
判断依据:
初速度为零,只受重力
自由落体运动
v0
G
(分运动)
(分运动)
(合运动)
水平方向:匀速直线运动
竖直方向:自由落体运动
速
度
大小:
方向:
一、平抛运动的速度
θ
vx
vy
v
O
x
y
v0
P (x,y)
θ叫速度偏转角
(4)位移的方向:
(2)平抛运动在竖直方向分位移:
(1)平抛运动在水平方向分位移:
(3)合位移:
1.平抛运动的位移
二、平抛运动的位移和轨迹
l
O
x
y
P (x,y)
B
A
v0
ɑ
ɑ叫位移偏转角
(3)结论:平抛运动的轨迹是一条抛物线。
(1)水平方向:匀速直线运动
(2)竖直方向:自由落体运动
消去 t 得:
2.平抛运动的轨迹
二、平抛运动的位移和轨迹
B
A
1.平抛运动的物体在某一点的速度方向和位移方向
相同吗?它们之间有什么关系?
问题设计
答案 方向不同.
平抛运动的两个推论
2.观察速度反向延长线与x轴的交点,你有什么发现?
答案 因为tan α= tan θ,可知B为此时水平位移的中点.
v
C
O
x
y
t
θ
vx
vy
α
x
y
竖直方向:
水平方向:
合位移:
合速度:
分运动规律
合运动规律
P
θ
Ox 中点
平抛运动的轨迹方程(两个分位移方程联立):
即平抛物体的运动轨迹是一个顶点在原点、开口向下的抛物线
平抛运动的理解
典例精析
例1 关于平抛物体的运动,以下说法正确的是( )
A.做平抛运动的物体,速度和加速度
都随时间的增加而增大
B.做平抛运动的物体仅受到重力的作
用,所以加速度保持不变
C.平抛物体的运动是匀变速运动
D.平抛物体的运动是变加速运动
BC
加速度恒定
加速曲线运动
匀变速曲线运动
解析
例2. 将一个物体以 10 m/s 的速度从 5 m 的高度水平抛出,落地时它的速度方向与地面的夹角 θ 是多少 (不计空气阻力,取 g = 10 m/s2)
解析:落地时,物体水平分速度:
vx= v0 = 10 m/s
vy 根据匀变速运动的规律,竖直方向分速度 vy 满足以下关系:
vy2 0 = 2gh,由此解出:vy= 10 m/s
tan θ = vy/vx = 1
物体落地时速度与地面的夹角是 45°
1. 小球从 h 高处以 v0 的初速度做平抛运动,求小球在空中的飞行时间 t 和水平射程 x 。
解:小球在竖直方向做自由落体运动,
由 得
小球在水平方向做匀速直线运动,水平射程
飞行时间仅与下落的高度h有关,与初速度 v0 无关。
水平射程(落地时的水平位移)与初速度 v0 和下落的高度 h 有关
x
v0
h
2. 小球从 h 高处以 v0 的初速度做平抛运动,求小球落地时速度 v 的大小。
x
v0
h
落体的速度 v 由初速度 v0 和下落高度 h 共同决定
v
vx
vy
1. 平抛运动在空中飞行时间:
与质量和初速度大小无关,只由高度 h 决定
2. 平抛运动的水平最大射程:
3. 落地速度
由初速度 v0 和下落高度 h 共同决定,与质量无关
由初速度 v0 和下落高度 h 共同决定,与质量无关
(1)理想化特点:平抛运动是一种理想化的模型,即把物体看成质点,抛出后只考虑重力作用,忽略空气阻力.
(2)匀变速特点:平抛运动的加速度恒定,即始终等于重力加速度.
(3)速度变化特点:任意两个相等的时间间隔内速度的变化相同,
Δv=gΔt,方向竖直向下,如下所示.
v0
gΔt
Δv=gΔt
Δv=gΔt
Δv=gΔt
2gΔt
3gΔt
平抛运动的三个特点
1. 概念:把物体以一定的初速度 v0 斜向上或斜向下抛出去,物体只在重力作用下所做的运动叫做斜抛运动。
2.斜抛运动的性质:由于斜抛运动的加速度是重力加速度,且与速度方向有夹角,因此,斜抛运动是匀变速曲线运动.
斜抛运动
x
水平方向初速度: Vox = Vo cos , ax = 0
竖直方向初速度: Voy = Vo sin , ay = g,方向向下
y
vox
voy
vo
射高H
射程S
水平方向:匀速直线运动
竖直方向:竖直上抛运动
斜上抛运动
位移:x=voxt= v0tcosθ
位移:
速度:vy=v0y-gt=v0sin θ-gt
速度:vx=v0x=v0cosθ
匀速直线运动
竖直上抛运动
X轴:
Y轴:
v0y
v0
x
v0x
y
0
v
vx
vy
合速度大小:
合速度方向:
合位移大小:
s
y
x
合位移方向:
分
解
斜抛运动的规律
平抛
课堂小结
斜抛
抛体运动的规律
思路:化曲为直
方法:运动的分解
水平方向:
竖直方向:
速度
位移
x=v0tcos
vx=v0cos
vy=v0sin - gt
【例1】. 如图所示,x 轴在水平地面内,y 轴沿竖直方向。图中画出了从 y 轴上沿 x 轴正向抛出的三个小球 a、b 和 c 的运动轨迹,其中 b 和 c 是从同一点抛出的。不计空气阻力,则( )
A. a 的飞行时间比 b 的长
B. b 和 c 的飞行时间相同
C. a 的水平速度比 b 的小
D. b 的初速度比 c 的大
BD
【例2】玩具轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A。已知A点高度为h=3.6m,山坡倾角为37°,g取10m/s2,由此可算出( )
A. 炸弹的飞行时间为0.8s
B. 轰炸机的飞行速度是8m/s
C. 轰炸机的飞行高度为5.2m
D. 炸弹飞行的水平位移为3.6m
A
【例3】 (2021·浙江高一月考)如图所示,从倾角为θ的足够长的斜面顶端P以速度v抛出一个小球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变为2v,则( )
A.小球的水平位移和竖直位移之比变为原来的2倍
B.夹角α将变原来的2倍
C.PQ间距一定为原来问距的2倍
D.空中的运动时间变为原来的2倍
D
1.某同学在某一水平直线上相同高度的A、B、C三个位置先后斜上抛出三个小球,结果三个小球都能够垂直击中墙壁的同一位置,设三次抛出的小球在空中飞行时间分别为t1、t2、t3,到达墙壁的速度分别为v1、v2、v3,不计空气阻力,则( )
A.t1>t2>t3 , v1>v2>v3
B.t1>t2>t3 , v1=v2=v3
C.t1=t2=t3 , v1>v2>v3
D.t1=t2=t3 , v1=v2=v3
A
C
B
C
题型1.多体平抛
2.如图所示,用6 m 长的轻绳将 A、B两球相连,两球相隔0.8 s先后从C点以4.5m/s的初速度水平抛出.那么,将A球抛出后经多长时间,A、B 间的轻绳刚好被拉直 (g=10m/s2)
【答案】1s
3.如图所示,一把玩具枪在同一高度以分别以速度2v和3v射出两颗子弹并击中竖直墙壁的A和B两点,下列说法正确的是( )
A.子弹击中A、B的运动时间之比为1:1
B.子弹击中A、B的运动时间之比为3:2
C.子弹击中A、B的竖直位移之比为2 :1
D.子弹击中A、B的竖直位移之比为9 :4
BD
题型2.各种落地方式的平抛
平抛时间由下落高度决定,不是离地高度
4.如图所示,从倾角为θ的足够长的斜面顶端P以速度v抛出一个小球,落在斜面上某处Q点,小球落在斜面上的速度与斜面的夹角为α,若把初速度变为2v,则( )
A.小球的水平位移和竖直位移之比变为原来的2倍
B.夹角α将变原来的2倍
C.PQ间距一定为原来间距的2倍
D.空中的运动时间变为原来的2倍
D
顺抛落地,“三角”一定
斜面上的顺抛
5.如图所示,小球以v0正对倾角为θ的斜面水平抛出,若小球垂直撞击斜面,则飞行时间t为(重力加速度为g)
( )
A.v0tanθ B.
C. D.
C
垂直落地,“一角”一定
斜面上垂直对抛1
6.如图所示,小球以v0正对倾角为θ的斜面水平抛出,若小球到达斜面的位移最小,则飞行时间t为(重力加速度为g)( )
A.v0tanθ B.
C. D.
D
垂直落地,“一角”一定
53
1.如图所示,水平地面上有一斜面山坡,山坡倾角为53 ,高为80m,一小球
从山坡顶端水平抛出,不计空气阻力,(重力加速度为g=10m/s2)求
(1)若初速度为20m/s时,求水平位移多大?
(2)若v0=12m/s,小球离斜面最远时的运动时间和最远距离?
【答案】(1)80m (2) 1.6s ;7.68m
(1)方法:分解速度和加速度法
(2)规律:沿斜面方向匀加速,垂直斜面先匀减速后匀加速
(3)对称性特点:
离斜面最远点时间和回落到斜面的时间对称,t=v0tanθ/g.
沿斜面方向的位移大小_______
(4)极值和临界分析:
离斜面有最大距离L=__________________
恰好落在斜面上的速度临界值V=______
不对称
斜面上平抛的运动分解处理和极值
v0x
v0y
v0
g
gy
gx
v
vy
v0
7.(多选)如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环的半径为R。一小球从A沿AB方向以速度V水平抛出,不计空气阻力,则( )
A.V不同时,小球在空中运动时间可能相同
B.V合适时有可能垂直撞击BC之间圆环
C. 如果抛出点在A的正上方时,有可能垂直撞击BC之间圆环
D. 如果抛出点水平向右侧移时,有可能垂直撞击BC之间圆环。
A
C
B
ACD
球面上垂直抛
题型2.常见平抛时间的求值方法总结
(1)位移法:
已知水平位移: t=x/v0 如撞击竖直墙壁,
已知竖直位移: 如撞击水平地面,
(2)速度法:竖直分速度一定:t=vy/g:
顺抛撞击斜面: t=vy/g=2v0tanθ/g
对抛速度垂直斜面:t=vy/g=v0/gtanθ
对抛位移垂直斜面:t=vy/g=2v0/gtanθ
8.如图所示,质量相同的、两质点从同一点分别以相同的水平速度沿轴正方向抛出,在竖直平面内运动,落地点为p1;沿光滑斜面运动,落地点为p2。和在同一水平面内,不计空气阻力,则下列说法中正确的是( )
A.A、B的运动时间相同
B.A、B沿轴方向的位移相同
C.A、B落地时的速度大小相同
D.A、B落地时的速度不同
CD
题型3.类平抛问题
D
9.质量m=4kg的质点静止在光滑水平面上的直角坐标系的原点,先用沿x轴正方向的力F1=8N作用了2s,然后撤去F1;再用沿y轴正方向的力F2=24N作用了1s.则质点在这3s内的轨迹为( )
10.如图所示,有一倾角为30°的光滑斜面,斜面长L为10m,一小球从斜面顶端以10m/s的速度在斜面上沿水平方向抛出.(g取10 m/s )求∶
(1)小球沿斜面滑到底端时的水平位移x.
(2)小球到达斜面底端时的速度大小.
【答案】(1)20m ; (2) 14.1m/s
1.类平抛定义:
物体具有一定初速度,只受到和初速度垂直方向的恒力作用的运动方式
2.类平抛的规律
(1)初速度方向:匀速直线运动
(2)恒力方向:初速度为零的匀加速直线运动a=F合/m
3.和平抛的比较
(1)初速度方向是任意的,不一定是水平方向
(2)恒力大小任意,方向不一定是竖直向下,但一定和初速度垂直。
(3)平抛的推论也适用于类平抛
4.解题思路:
(1)求合力大小和方向,求加速度大小和方向
(2)确认初速度方向和加速度方向是否垂直
(3)沿初速度和加速度方向进行运动分解
(4)求解相关量
题型3.类平抛运动总结
(θ≠2α)
1.如图所示,乒乓球水平发球点在桌面的中心处,以不同速率,朝右侧以不同方向水平发射乒乓球,发球点高度为3h,球网高度为h,桌面长和宽分别为L1和L2,要成功发球,不计空气阻力,则乒乓球水平抛出的初速度的取值范围?
题型4、平抛运动中的临界极值问题
【例1】如图所示,窗子上、下沿间的高度H=1.6 m,墙的厚度d=0.4 m,某人在离墙壁L=1.4 m、距窗子上沿h=0.2 m处的P点,将可视为质点的小物体以速度v平行墙面方向水平抛出,小物体直接穿过窗口并落在水平地面上,g取10 m/s2.则v的取值范围是( )
A.v>7 m/s B.v<2.3 m/s
C.3 m/s
C
2.障碍物平抛的速度临界问题总结
(1)作运动轨迹的速度渐进动态图
(2)确定临界状态对应的竖直位移一定时的最大最小水平位移
(3)求对应既定竖直位移对应的时间
(4)求最大最小水平位移的初速度,确定其范围。
