2.变量与函数
图片预览






文档简介
课件18张PPT。
第18章函数及其图象§18.1变量与函数 在某一变化过程中,可以取不同
数值的量,叫做变量。变 量: 在一个变化过程中,数值始终
保持不变的量,称为常量。常 量:S=60ts=x(5-x)变 量:变 量:变 量:变 量:S, tc,rS, nS, x常 量:常 量:常 量:常 量:605s=(n-2) ×18002,180复习回顾定义(1)在 S= 60t 中,S是t 的函数,(2)在 l =0.5m+10中, t 是自变量; l 是 m 的函数, m 是自变量;一般地,在一个变化过程中有两个变量x与y,如果对于x每 一个确定的值,y都有唯一的值与它对应,那么我们就说x是自变量,此时也称 y是x的函数。 区别与观察下面关系式 y=x+1
当x=1时,y=2y=3当x=2时,(2) y2 =xy=4当x=3时,y=5当x=4时,y随x的变化而变化当x=1时,y=+1或-1y=+2或-2当x=4时,y=+3或-3当x=9时,y=+4或-4当x=16时,关系式(1)y=x+1中对于每个x的值,
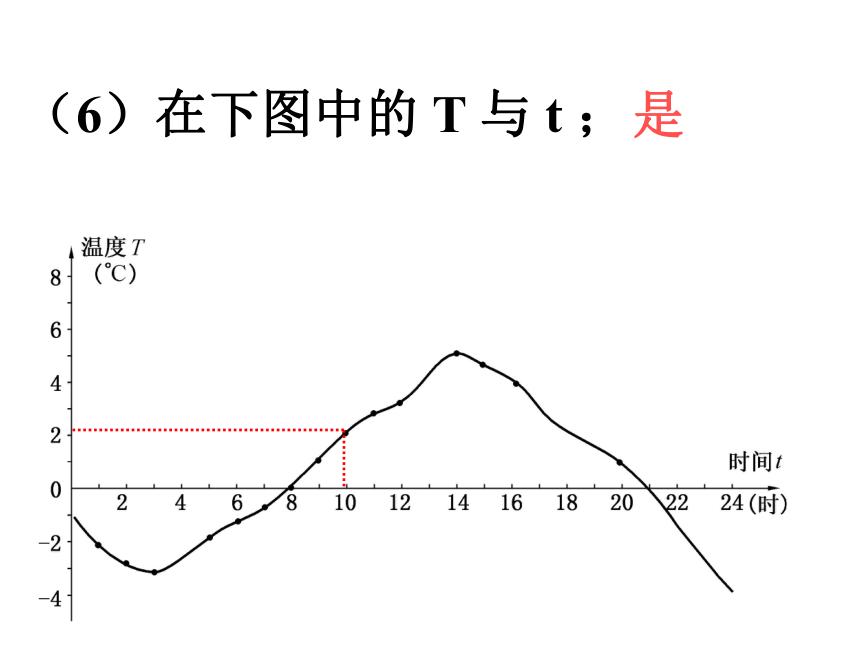
y都有唯一的值,与x对应例 下列问题中的变量y是不是x的函数?是(1)在 y = 2x 中的y与x;是不是是不是是(6)在下图中的 T 与 t ;注意:用式子表示的函数,一般来说,自变量只能取使式子有意义的值。 想一想判断 是否为y是x的函数? 你能说出使该函数式有意义的自变量x的取值范围吗?自变量x的取值范围是:例、求出下列函数中自变量的取值范围(1)y=2x(1) x为任何实数(2) n≥1(3) x≠-2(4)k≤1且k ≠-1解:例、求出下列函数中自变量的取值范围(1)y=2x(5)n 边形的内角和公式S = (n-2)1800(5) n≥3 的整数解:函数自变量取值范围的条件:(2)开偶数次方中的被开方数必须
大于等于0;(1)分母不等于0;(3)符合实际意义。当 x = 1时,y = 1.y = 1叫做当 x = 1 时的函数值函数值是由自变量所取的值来确定的函数值是由自变量所取的值来确定的综合运用一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。(1)写出表示y与x的函数关系的式子。(2)指出自变量x的取值范围(3)汽车行驶200 km时,油箱中还有多少油?Y = 50-0.1x0 ≤ x ≤ 500y = 50-0.1×200 =30答:油箱中还有油 30 L(3) 腰长AB=3时,底边的长.(2) 自变量的取值范围;(1) 关于 的函数解析式; 当 x = 6时, y=10 – 2x的值是多少?对本例有意义吗?当 x = 2 呢?想一想(2)在求自变量的取值范围时,要从两个方面来考虑:
①代数式要有意义;②要符合实际.归纳:(1)在求函数解析式时,可以先得到函数与自变量之
间的等式,然后解出函数关于自变量的函数解析式;1.用60m的篱笆围成矩形。写出矩形的面积S与一边长l 的关系式。 2.在前面的用60m的篱笆围成矩形的题中,如果使矩形一边靠墙,另三边用篱笆围成。写出矩形的面积S与一边长l 的关系式。 (1)??写出矩形面积S(㎡)与平行于墙的一边长 l (m)的关系式;
(2)??写出矩形面积S(㎡)与垂直于墙的一边长 l (m)的关系式;
(3)指出上面各式中的常量与变量,函数与自变量。
小结1、进一步理解函数的概念;2、会求函数的关系式3、能求函数自变量的取值范围4、会求函数值
第18章函数及其图象§18.1变量与函数 在某一变化过程中,可以取不同
数值的量,叫做变量。变 量: 在一个变化过程中,数值始终
保持不变的量,称为常量。常 量:S=60ts=x(5-x)变 量:变 量:变 量:变 量:S, tc,rS, nS, x常 量:常 量:常 量:常 量:605s=(n-2) ×18002,180复习回顾定义(1)在 S= 60t 中,S是t 的函数,(2)在 l =0.5m+10中, t 是自变量; l 是 m 的函数, m 是自变量;一般地,在一个变化过程中有两个变量x与y,如果对于x每 一个确定的值,y都有唯一的值与它对应,那么我们就说x是自变量,此时也称 y是x的函数。 区别与观察下面关系式 y=x+1
当x=1时,y=2y=3当x=2时,(2) y2 =xy=4当x=3时,y=5当x=4时,y随x的变化而变化当x=1时,y=+1或-1y=+2或-2当x=4时,y=+3或-3当x=9时,y=+4或-4当x=16时,关系式(1)y=x+1中对于每个x的值,
y都有唯一的值,与x对应例 下列问题中的变量y是不是x的函数?是(1)在 y = 2x 中的y与x;是不是是不是是(6)在下图中的 T 与 t ;注意:用式子表示的函数,一般来说,自变量只能取使式子有意义的值。 想一想判断 是否为y是x的函数? 你能说出使该函数式有意义的自变量x的取值范围吗?自变量x的取值范围是:例、求出下列函数中自变量的取值范围(1)y=2x(1) x为任何实数(2) n≥1(3) x≠-2(4)k≤1且k ≠-1解:例、求出下列函数中自变量的取值范围(1)y=2x(5)n 边形的内角和公式S = (n-2)1800(5) n≥3 的整数解:函数自变量取值范围的条件:(2)开偶数次方中的被开方数必须
大于等于0;(1)分母不等于0;(3)符合实际意义。当 x = 1时,y = 1.y = 1叫做当 x = 1 时的函数值函数值是由自变量所取的值来确定的函数值是由自变量所取的值来确定的综合运用一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。(1)写出表示y与x的函数关系的式子。(2)指出自变量x的取值范围(3)汽车行驶200 km时,油箱中还有多少油?Y = 50-0.1x0 ≤ x ≤ 500y = 50-0.1×200 =30答:油箱中还有油 30 L(3) 腰长AB=3时,底边的长.(2) 自变量的取值范围;(1) 关于 的函数解析式; 当 x = 6时, y=10 – 2x的值是多少?对本例有意义吗?当 x = 2 呢?想一想(2)在求自变量的取值范围时,要从两个方面来考虑:
①代数式要有意义;②要符合实际.归纳:(1)在求函数解析式时,可以先得到函数与自变量之
间的等式,然后解出函数关于自变量的函数解析式;1.用60m的篱笆围成矩形。写出矩形的面积S与一边长l 的关系式。 2.在前面的用60m的篱笆围成矩形的题中,如果使矩形一边靠墙,另三边用篱笆围成。写出矩形的面积S与一边长l 的关系式。 (1)??写出矩形面积S(㎡)与平行于墙的一边长 l (m)的关系式;
(2)??写出矩形面积S(㎡)与垂直于墙的一边长 l (m)的关系式;
(3)指出上面各式中的常量与变量,函数与自变量。
小结1、进一步理解函数的概念;2、会求函数的关系式3、能求函数自变量的取值范围4、会求函数值
