鲁教版九年级数学上册第2章2.1锐角三角函数测试题(含答案)
文档属性
| 名称 | 鲁教版九年级数学上册第2章2.1锐角三角函数测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 96.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-14 00:00:00 | ||
图片预览


文档简介
鲁教版九年级数学上册第2章2.1锐角三角函数测试题(含答案)
一.选择题(共12小题)
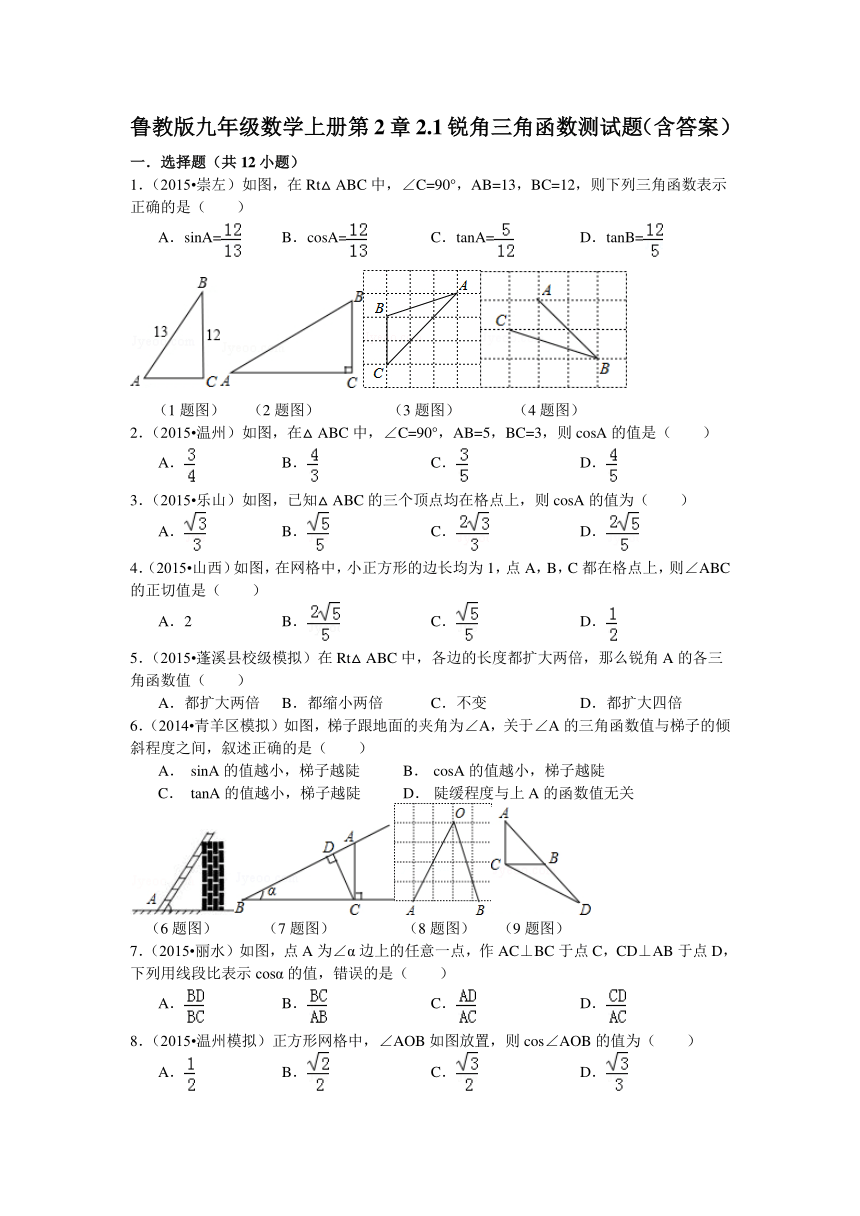
1.(2015 崇左)如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.sinA= B. cosA= C. tanA= D. tanB=
(1题图) (2题图) (3题图) (4题图)
2.(2015 温州)如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
A. B. C. D.
3.(2015 乐山)如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
A. B. C. D.
4.(2015 山西)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A.2 B. C. D.
5.(2015 蓬溪县校级模拟)在Rt△ABC中,各边的长度都扩大两倍,那么锐角A的各三角函数值( )
A.都扩大两倍 B. 都缩小两倍 C. 不变 D. 都扩大四倍
6.(2014 青羊区模拟)如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A. sinA的值越小,梯子越陡 B. cosA的值越小,梯子越陡
C. tanA的值越小,梯子越陡 D. 陡缓程度与上A的函数值无关
(6题图) (7题图) (8题图) (9题图)
7.(2015 丽水)如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
8.(2015 温州模拟)正方形网格中,∠AOB如图放置,则cos∠AOB的值为( )
A. B. C. D.
9.(2015 大庆模拟)如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=,则tanA=( )
A. B. 1 C. D.
10.(2015 甘谷县二模)在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A. B. C. D.
11.(2015 滨海县一模)如图,在平面直角坐标系中,P是∠1的边OA上一点,点P的坐标为(3,4),则sin∠1的值为( )
A. B. C. D.
(11题图) (12题图) (13题图) (14题图)
12.(2015 孝义市一模)如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan∠DCB的值是( )
A. B. C. D.
二.填空题(共5小题)
13.(2015 柳州)如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB= .
14.(2015 巴中)如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
15.(2015 温州二模)如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于 .
(15题图) (16题图) (18题图)
16.(2015 简阳市模拟)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为 .
17.(2015春 江苏校级期中)在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA= .
三.解答题(共4小题)
(1)如图,∠DBC=30°,AB=DB,利用此图求tan75°= .
(2)根据你所掌握的知识,试求出tan22.5°的值.
19.(2012 南岗区校级模拟)矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,求tan∠AFE.
20.(2013秋 北湖区校级期中)在△ABC中,∠C=90°,BC=8cm,tanA=,求AC的长.
21.(2015春 西安校级月考)△ABC中,∠C=90°,BC=3,AB=5,求sinA,cosA,tanA的值.
鲁教版九年级数学上册第2章2.1锐角三角函数测试题参考答案
一.选择题(共12小题)
1.A.2.D.3.D.4.D.5.C.6.B.7.C.8.B.9.A.10.C.11.C.12.D.
二.填空题(共5小题)
13. .14. .15. .16. .17. .
三.解答题(共4小题)
18.(1)解:∵AB=BD,∴∠A=∠ADB.
∵∠DBC=30°=2∠A,
∴∠A=15°,∠ADC=75°.
设CD=x,∴AB=BD===2x,
BC=CD×cot∠DBC=x,
AC=AB+BC=(2+)x,
∴tan∠ADC=tan75°
=AC:CD
=2+.
(2)构造图形:如图,令AC=BC=1,∠ACB=90°,则AB=
延长CB至D,使得BD=AB,易得∠ADB=22.5°
在Rt△ACD中,.
19.解:根据图形有:∠AFE+∠EFC+∠BFC=180°,
根据折叠的性质,∠EFC=∠EDC=90°,
即∠AFE+∠BFC=90°,
而Rt△BCF中,有∠BCF+∠BFC=90°,
易得∠AFE=∠BCF,
在Rt△BFC,
根据折叠的性质,有CF=CD,
在Rt△BFC中,BC=8,CF=CD=10,
由勾股定理易得:BF=6,
则tan∠BCF=;
故有tan∠AFE=tan∠BCF=;
答:tan∠AFE=.
20.解:∵Rt△ABC中,∠C=90°,BC=3,AB=5,∴AC==4,
∴sinA==; cosA==; tanA==.
21.解:∵tanA=,∴=,
∵BC=8cm,
∴AC=6cm.
一.选择题(共12小题)
1.(2015 崇左)如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.sinA= B. cosA= C. tanA= D. tanB=
(1题图) (2题图) (3题图) (4题图)
2.(2015 温州)如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
A. B. C. D.
3.(2015 乐山)如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
A. B. C. D.
4.(2015 山西)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A.2 B. C. D.
5.(2015 蓬溪县校级模拟)在Rt△ABC中,各边的长度都扩大两倍,那么锐角A的各三角函数值( )
A.都扩大两倍 B. 都缩小两倍 C. 不变 D. 都扩大四倍
6.(2014 青羊区模拟)如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A. sinA的值越小,梯子越陡 B. cosA的值越小,梯子越陡
C. tanA的值越小,梯子越陡 D. 陡缓程度与上A的函数值无关
(6题图) (7题图) (8题图) (9题图)
7.(2015 丽水)如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
8.(2015 温州模拟)正方形网格中,∠AOB如图放置,则cos∠AOB的值为( )
A. B. C. D.
9.(2015 大庆模拟)如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=,则tanA=( )
A. B. 1 C. D.
10.(2015 甘谷县二模)在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A. B. C. D.
11.(2015 滨海县一模)如图,在平面直角坐标系中,P是∠1的边OA上一点,点P的坐标为(3,4),则sin∠1的值为( )
A. B. C. D.
(11题图) (12题图) (13题图) (14题图)
12.(2015 孝义市一模)如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan∠DCB的值是( )
A. B. C. D.
二.填空题(共5小题)
13.(2015 柳州)如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB= .
14.(2015 巴中)如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
15.(2015 温州二模)如图,△ABC的顶点都是正方形网格中的格点,则tan∠BAC等于 .
(15题图) (16题图) (18题图)
16.(2015 简阳市模拟)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为 .
17.(2015春 江苏校级期中)在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA= .
三.解答题(共4小题)
(1)如图,∠DBC=30°,AB=DB,利用此图求tan75°= .
(2)根据你所掌握的知识,试求出tan22.5°的值.
19.(2012 南岗区校级模拟)矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,求tan∠AFE.
20.(2013秋 北湖区校级期中)在△ABC中,∠C=90°,BC=8cm,tanA=,求AC的长.
21.(2015春 西安校级月考)△ABC中,∠C=90°,BC=3,AB=5,求sinA,cosA,tanA的值.
鲁教版九年级数学上册第2章2.1锐角三角函数测试题参考答案
一.选择题(共12小题)
1.A.2.D.3.D.4.D.5.C.6.B.7.C.8.B.9.A.10.C.11.C.12.D.
二.填空题(共5小题)
13. .14. .15. .16. .17. .
三.解答题(共4小题)
18.(1)解:∵AB=BD,∴∠A=∠ADB.
∵∠DBC=30°=2∠A,
∴∠A=15°,∠ADC=75°.
设CD=x,∴AB=BD===2x,
BC=CD×cot∠DBC=x,
AC=AB+BC=(2+)x,
∴tan∠ADC=tan75°
=AC:CD
=2+.
(2)构造图形:如图,令AC=BC=1,∠ACB=90°,则AB=
延长CB至D,使得BD=AB,易得∠ADB=22.5°
在Rt△ACD中,.
19.解:根据图形有:∠AFE+∠EFC+∠BFC=180°,
根据折叠的性质,∠EFC=∠EDC=90°,
即∠AFE+∠BFC=90°,
而Rt△BCF中,有∠BCF+∠BFC=90°,
易得∠AFE=∠BCF,
在Rt△BFC,
根据折叠的性质,有CF=CD,
在Rt△BFC中,BC=8,CF=CD=10,
由勾股定理易得:BF=6,
则tan∠BCF=;
故有tan∠AFE=tan∠BCF=;
答:tan∠AFE=.
20.解:∵Rt△ABC中,∠C=90°,BC=3,AB=5,∴AC==4,
∴sinA==; cosA==; tanA==.
21.解:∵tanA=,∴=,
∵BC=8cm,
∴AC=6cm.
