四川省内江市威远县重点中学2023-2024学年八年级下学期开学考试数学试题(含答案)
文档属性
| 名称 | 四川省内江市威远县重点中学2023-2024学年八年级下学期开学考试数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 11:10:06 | ||
图片预览




文档简介
四川省威远县重点中学2024年春入学调研八年级数学试卷
学校:___________姓名:___________班级:___________考号:___________
时间120分,满分120分
一、单选题(每小题4分,共48分)
1.在下列实数、0.31、、、3.602 4×103、、1.212 212 221 …(每两个1之间依次多一个2)中,无理数的个数为( )
A.1 B.2 C.3 D.4
2.如图,乐乐在∠ABC的平分线上任取一点P,并作PE⊥AB于点E,经测量知PE=2 cm,由此可以推断点P到BC的距离为( )
A.4 cm B.3 cm C.2 cm D.1 cm
3.白日登山望烽火,黄昏饮马傍交河.诗中隐含着一个有趣的数学问题:诗中将军在观望烽火之后从山脚上的A点出发,奔向小河旁边的点饮马,饮马后再到点宿营,若到水平直线(表示小河)的距离分别是2,1,两点之间水平距离是4,则最小值为( )
A.3 B.4 C.5 D.6
4.如图,中,,将折叠后,使得点B与点A重合,.折痕分别交、于点D、E.如果,的周长为,那么的长为( )
A.10cm B.12cm C.13cm D.17cm
5.“折竹抵地”问题源自《九章算术》中:“今有竹高一丈,末折抵地,去本四尺,问折者高几何 ”意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,问折断处离地面的高度是( )
A.尺 B.尺 C.5尺 D.4尺
6.某校为了解七年级1200名新生的上学方式,随机对该年级部分学生的上学方式(乘车、步行、骑车)进行了调查,并根据调查结果绘制了条形统计图和扇形统计图,则下列判断错误的是( )
A.调查的学生中步行上学的有8名
B.扇形统计图中步行的学生人数所占的圆心角是
C.该校七年级学生中骑车上学的约有360名
D.扇形统计图中骑车的学生人数所占的圆心角是
7.若,则的正确结果是( )
A.-1 B.1 C.-5 D.5
8.若9x2+mxy+16y2是一个完全平方式,那m的值是( )
A.±12 B.-12 C.±24 D.-24
9.下列多项式,能用公式法分解因式的有( )
① ② ③ ④
⑤ ⑥
A.2个 B.3个 C.4个 D.5个
10.如图所示,在中,的垂直平分线交于点,交于点,如果,则的周长是( )
A. B. C. D.
11.在钝角三角形ABC中,把AB=AC,D是BC上一点,AD把ABC分成两个等腰三角形,则BAC的度数为( )
A. B. C. D.
12.如图,点是线段上一点,、是等边三角形与交于点,与交于点,与交于点下列结论:①;②;③;④;⑤平分其中正确的是( )
A.①③④ B.①②③⑤ C.①③⑤ D.①②③④⑤
二、填空题(每小题4分,共16分)
13.在一组数据中,第1个数的频率是0.2,频数是30,第2个数的频率是0.5,则第2个数的频数是 .
14.如图,飞机在空中水平飞行,某一时刻刚好飞到小明头顶正上方4 000米处,经过了20秒,飞机距离小明头顶5 000米,则飞机飞行的速度是 米/秒.
15.已知a2+2a+b2-6b+10=0,那么a= ,b= .
16.如图所示,△ABC为等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,有下列四个结论:①点P在∠BAC的平分线上;②AS=AR;③QP∥AB;④△BRP≌△CSP.其中,正确的有 (填序号即可).
三、解答题(6个小题,共56分)
17.(12分)(1)计算: (2)求x的值:
(3)先化简,再求值:,其中.
18.(8分)阅读下面的解答过程.
已知x2-2x-3=0,求x3+x2-9x-8的值.
解:因为x2-2x-3=0,所以x2=2x+3.
所以x3+x2-9x-8=x·x2+x2-9x-8=x·(2x+3)+(2x+3)-9x-8=2x2+3x+2x+3-9x-8=2(2x+3)-4x-5=1.
请你仿照上题的做法完成下面的题.
已知x2-5x+1=0,求x3-4x2-4x-1的值.
19.(8分)某校学生会为了丰富学生的课外活动,准备组织一次球类比赛.他们通过调查问卷的方式,随机抽查了部分学生,了解了学生们最喜欢的球类运动,并绘制成不完全统计图.
调查问卷:你最喜欢的球类运动是( )(单选)
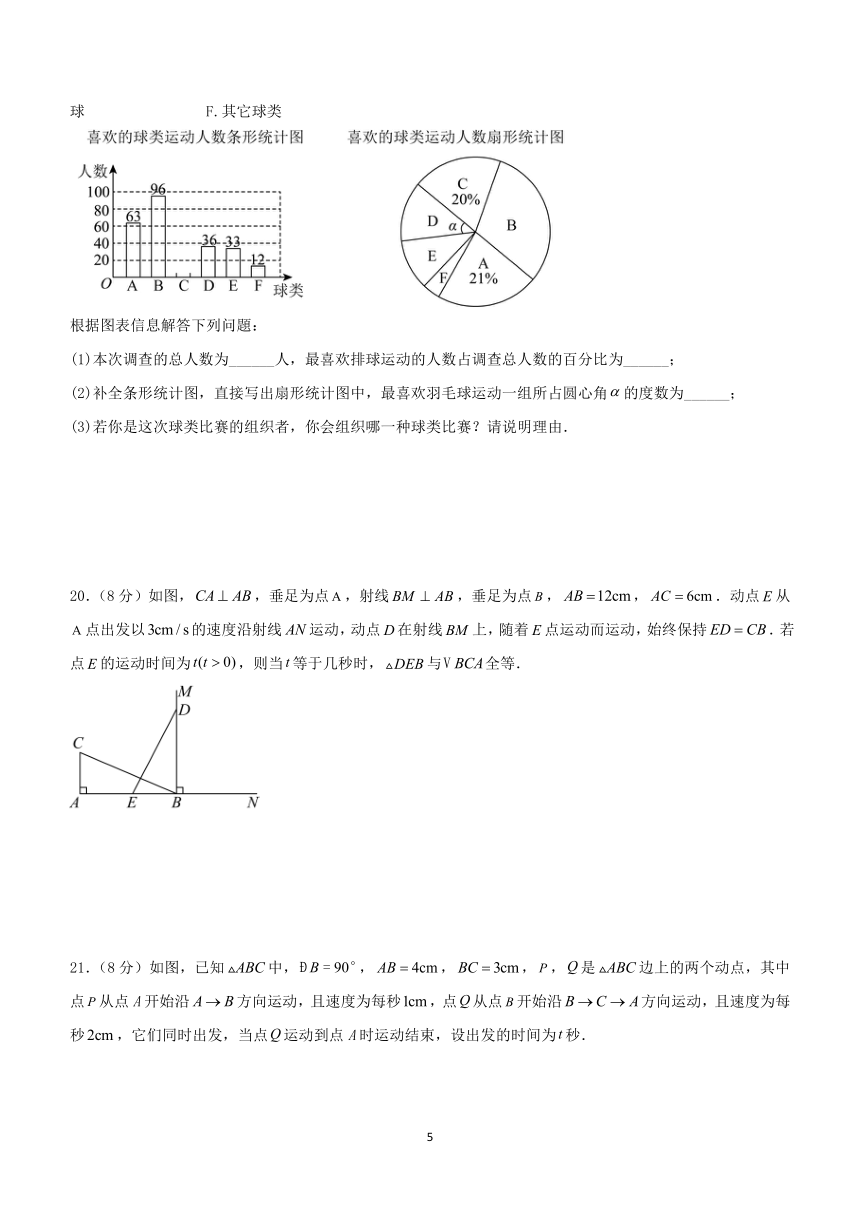
A.足球 B.乒乓球 C.篮球 D.羽毛球 E.排球 F.其它球类
根据图表信息解答下列问題:
(1)本次调查的总人数为______人,最喜欢排球运动的人数占调查总人数的百分比为______;
(2)补全条形统计图,直接写出扇形统计图中,最喜欢羽毛球运动一组所占圆心角的度数为______;
(3)若你是这次球类比赛的组织者,你会组织哪一种球类比赛?请说明理由.
20.(8分)如图,,垂足为点,射线,垂足为点,,.动点从点出发以的速度沿射线运动,动点在射线上,随着点运动而运动,始终保持.若点的运动时间为,则当等于几秒时,与全等.
21.(8分)如图,已知中,,,,,是边上的两个动点,其中点从点A开始沿方向运动,且速度为每秒,点从点开始沿方向运动,且速度为每秒,它们同时出发,当点运动到点A时运动结束,设出发的时间为秒.
(1)出发1秒时,求的长;
(2)当点在边上运动时,通过计算说明能否把的周长平分;
(3)当点在边上运动时,请直接写出能使成为等腰三角形的运动时间.
22.(1)如图1,四边形中,,是上一点,平分,平分.则线段的长度满足的数量关系为______;
(2)如图2,将(1)中的条件“”改为“”,其他条件不变,(1)中的结论是否还成立,如果成立,请说明理由;如果不成立,请举出反例;
(3)将(1)中的条件“”改为“”,其他条件不变,试探究线段之间的数量关系,并说明理由.
参考答案:
1.C 2.C 3.C 4.C 5.A 6.D 7.A 8.C 9.A 10.D 11.D 12.B
13.75. 14.150 15. -1 3 16.①②③④
17.解:(1)
(2)∵
∴
∴
∴
(3)
当时,
.
18.解:∵x2-5x+1=0,
∴x2=5x-1,
∴x3-4x2-4x-1=x·x2-4x2-4x-1=x·(5x-1)-4(5x-1)-4x-1
=5x2-x-20x+4-4x-1
=5(5x-1)-25x+3
=-2.
19.(1)解:本次调查的总人数为:(人),
最喜欢排球运动的人数占调查总人数的百分比为:
故答案为:,;
(2)解:喜欢篮球的人数为:(人)
补全条形统计图如下:
最喜欢羽毛球运动一组所占圆心角的度数为:,
故答案为:
(3)解:组织乒乓球比赛,因为在调查的人中,最喜欢乒乓球运动的人最多.
20.解:①当在线段上,时,
,
,
,
点 的运动时间为 秒.
②当在上,时,
,
,
.
点 的运动时间为 秒.
③当在上,时,
点的运动时间为 秒
④当在线段上,时,这时在点未动,因此时间为秒不符合题意.
故答案为:或或.
21.(1)解:,
,
∵,
∴;
(2)解:由勾股定理得:,
根据题意得:,,,
若能把的周长平分,则,
即,
解得:,
此时,
∴不合题意,
∴点Q在边上运动时,不能把的周长平分;
(3)解:①当时,如图1所示
则,
∵,
∴,,
∴,
∴,
∴,
∴,
∴(秒);
②当时,如图2所示:
则,
∴(秒);
③当时,如图3所示:
过B点作于点E,
则,
∴,
∴,
∴,
∴(秒),
由上可知,当t的值为秒或3秒或秒时,为等腰三角形.
22.(1)解:如图,过点有作,
,
.
又,
.
平分,
.
又.
.
.
同理可得.
.
故答案为:;
(2)成立,理由如下:
在上截取,连接,如图所示:
、分别平分、,
,,
在和中,
,
,
,,
,
在和中,
,
,
,
;
(3),理由如下:
在上截取,,连接,如图所示:
、分别平分、,
,,
在和中,
,
,
在和中,
,,
,
,
为等边三角形
,
;
学校:___________姓名:___________班级:___________考号:___________
时间120分,满分120分
一、单选题(每小题4分,共48分)
1.在下列实数、0.31、、、3.602 4×103、、1.212 212 221 …(每两个1之间依次多一个2)中,无理数的个数为( )
A.1 B.2 C.3 D.4
2.如图,乐乐在∠ABC的平分线上任取一点P,并作PE⊥AB于点E,经测量知PE=2 cm,由此可以推断点P到BC的距离为( )
A.4 cm B.3 cm C.2 cm D.1 cm
3.白日登山望烽火,黄昏饮马傍交河.诗中隐含着一个有趣的数学问题:诗中将军在观望烽火之后从山脚上的A点出发,奔向小河旁边的点饮马,饮马后再到点宿营,若到水平直线(表示小河)的距离分别是2,1,两点之间水平距离是4,则最小值为( )
A.3 B.4 C.5 D.6
4.如图,中,,将折叠后,使得点B与点A重合,.折痕分别交、于点D、E.如果,的周长为,那么的长为( )
A.10cm B.12cm C.13cm D.17cm
5.“折竹抵地”问题源自《九章算术》中:“今有竹高一丈,末折抵地,去本四尺,问折者高几何 ”意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,问折断处离地面的高度是( )
A.尺 B.尺 C.5尺 D.4尺
6.某校为了解七年级1200名新生的上学方式,随机对该年级部分学生的上学方式(乘车、步行、骑车)进行了调查,并根据调查结果绘制了条形统计图和扇形统计图,则下列判断错误的是( )
A.调查的学生中步行上学的有8名
B.扇形统计图中步行的学生人数所占的圆心角是
C.该校七年级学生中骑车上学的约有360名
D.扇形统计图中骑车的学生人数所占的圆心角是
7.若,则的正确结果是( )
A.-1 B.1 C.-5 D.5
8.若9x2+mxy+16y2是一个完全平方式,那m的值是( )
A.±12 B.-12 C.±24 D.-24
9.下列多项式,能用公式法分解因式的有( )
① ② ③ ④
⑤ ⑥
A.2个 B.3个 C.4个 D.5个
10.如图所示,在中,的垂直平分线交于点,交于点,如果,则的周长是( )
A. B. C. D.
11.在钝角三角形ABC中,把AB=AC,D是BC上一点,AD把ABC分成两个等腰三角形,则BAC的度数为( )
A. B. C. D.
12.如图,点是线段上一点,、是等边三角形与交于点,与交于点,与交于点下列结论:①;②;③;④;⑤平分其中正确的是( )
A.①③④ B.①②③⑤ C.①③⑤ D.①②③④⑤
二、填空题(每小题4分,共16分)
13.在一组数据中,第1个数的频率是0.2,频数是30,第2个数的频率是0.5,则第2个数的频数是 .
14.如图,飞机在空中水平飞行,某一时刻刚好飞到小明头顶正上方4 000米处,经过了20秒,飞机距离小明头顶5 000米,则飞机飞行的速度是 米/秒.
15.已知a2+2a+b2-6b+10=0,那么a= ,b= .
16.如图所示,△ABC为等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,有下列四个结论:①点P在∠BAC的平分线上;②AS=AR;③QP∥AB;④△BRP≌△CSP.其中,正确的有 (填序号即可).
三、解答题(6个小题,共56分)
17.(12分)(1)计算: (2)求x的值:
(3)先化简,再求值:,其中.
18.(8分)阅读下面的解答过程.
已知x2-2x-3=0,求x3+x2-9x-8的值.
解:因为x2-2x-3=0,所以x2=2x+3.
所以x3+x2-9x-8=x·x2+x2-9x-8=x·(2x+3)+(2x+3)-9x-8=2x2+3x+2x+3-9x-8=2(2x+3)-4x-5=1.
请你仿照上题的做法完成下面的题.
已知x2-5x+1=0,求x3-4x2-4x-1的值.
19.(8分)某校学生会为了丰富学生的课外活动,准备组织一次球类比赛.他们通过调查问卷的方式,随机抽查了部分学生,了解了学生们最喜欢的球类运动,并绘制成不完全统计图.
调查问卷:你最喜欢的球类运动是( )(单选)
A.足球 B.乒乓球 C.篮球 D.羽毛球 E.排球 F.其它球类
根据图表信息解答下列问題:
(1)本次调查的总人数为______人,最喜欢排球运动的人数占调查总人数的百分比为______;
(2)补全条形统计图,直接写出扇形统计图中,最喜欢羽毛球运动一组所占圆心角的度数为______;
(3)若你是这次球类比赛的组织者,你会组织哪一种球类比赛?请说明理由.
20.(8分)如图,,垂足为点,射线,垂足为点,,.动点从点出发以的速度沿射线运动,动点在射线上,随着点运动而运动,始终保持.若点的运动时间为,则当等于几秒时,与全等.
21.(8分)如图,已知中,,,,,是边上的两个动点,其中点从点A开始沿方向运动,且速度为每秒,点从点开始沿方向运动,且速度为每秒,它们同时出发,当点运动到点A时运动结束,设出发的时间为秒.
(1)出发1秒时,求的长;
(2)当点在边上运动时,通过计算说明能否把的周长平分;
(3)当点在边上运动时,请直接写出能使成为等腰三角形的运动时间.
22.(1)如图1,四边形中,,是上一点,平分,平分.则线段的长度满足的数量关系为______;
(2)如图2,将(1)中的条件“”改为“”,其他条件不变,(1)中的结论是否还成立,如果成立,请说明理由;如果不成立,请举出反例;
(3)将(1)中的条件“”改为“”,其他条件不变,试探究线段之间的数量关系,并说明理由.
参考答案:
1.C 2.C 3.C 4.C 5.A 6.D 7.A 8.C 9.A 10.D 11.D 12.B
13.75. 14.150 15. -1 3 16.①②③④
17.解:(1)
(2)∵
∴
∴
∴
(3)
当时,
.
18.解:∵x2-5x+1=0,
∴x2=5x-1,
∴x3-4x2-4x-1=x·x2-4x2-4x-1=x·(5x-1)-4(5x-1)-4x-1
=5x2-x-20x+4-4x-1
=5(5x-1)-25x+3
=-2.
19.(1)解:本次调查的总人数为:(人),
最喜欢排球运动的人数占调查总人数的百分比为:
故答案为:,;
(2)解:喜欢篮球的人数为:(人)
补全条形统计图如下:
最喜欢羽毛球运动一组所占圆心角的度数为:,
故答案为:
(3)解:组织乒乓球比赛,因为在调查的人中,最喜欢乒乓球运动的人最多.
20.解:①当在线段上,时,
,
,
,
点 的运动时间为 秒.
②当在上,时,
,
,
.
点 的运动时间为 秒.
③当在上,时,
点的运动时间为 秒
④当在线段上,时,这时在点未动,因此时间为秒不符合题意.
故答案为:或或.
21.(1)解:,
,
∵,
∴;
(2)解:由勾股定理得:,
根据题意得:,,,
若能把的周长平分,则,
即,
解得:,
此时,
∴不合题意,
∴点Q在边上运动时,不能把的周长平分;
(3)解:①当时,如图1所示
则,
∵,
∴,,
∴,
∴,
∴,
∴,
∴(秒);
②当时,如图2所示:
则,
∴(秒);
③当时,如图3所示:
过B点作于点E,
则,
∴,
∴,
∴,
∴(秒),
由上可知,当t的值为秒或3秒或秒时,为等腰三角形.
22.(1)解:如图,过点有作,
,
.
又,
.
平分,
.
又.
.
.
同理可得.
.
故答案为:;
(2)成立,理由如下:
在上截取,连接,如图所示:
、分别平分、,
,,
在和中,
,
,
,,
,
在和中,
,
,
,
;
(3),理由如下:
在上截取,,连接,如图所示:
、分别平分、,
,,
在和中,
,
,
在和中,
,,
,
,
为等边三角形
,
;
同课章节目录
