８.一次函数的性质

课件20张PPT。18.3.3 一次函数的性质

1 一次函数的一般形式是
， 它的图象是 一般情况下，我们画一次函数的图象，取点 和 比较
简便。 Y=kx+b(k.b是常数，k≠0)一条直线（0，b)(－b/k , 0) 2 正比例函数的一般形式是 3 正比例函数与一次函数的关系是Y=kx(k是常数k≠0)。正比例函数是特殊的一次函数。对一次函数y=x+4，x依次取-3,-2,-1,0,1,2,3
逐渐增大的过程中，y的值是否也在增大？
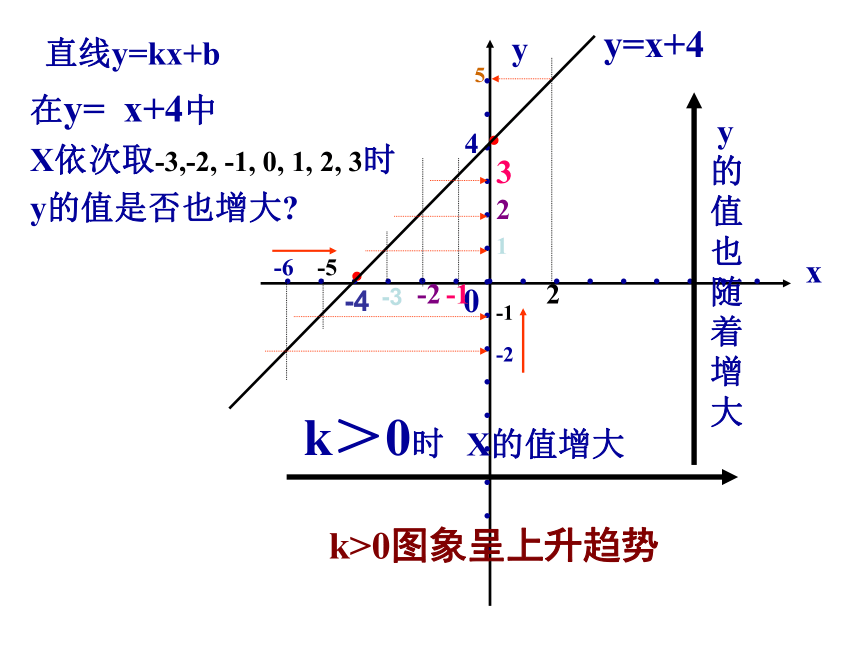
对y=-x+4呢？1234 5 6 77654 3 2 1y增大y减小试一试直线y=kx+b在y= x+4中
X依次取-3,-2, -1, 0, 1, 2, 3时
y的值是否也增大?
··y=x+44k>0图象呈上升趋势-4-3直线y=kx+by= - x+4
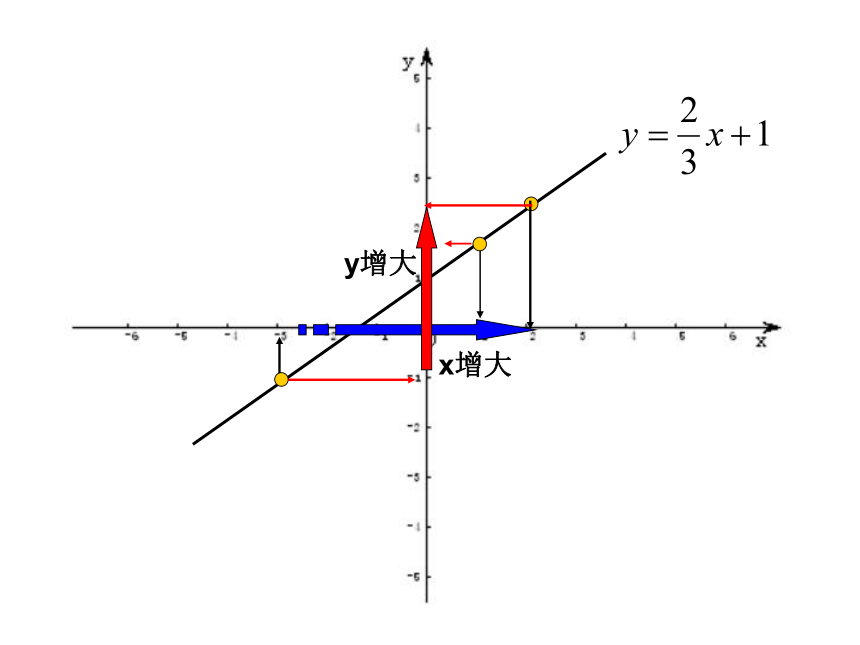
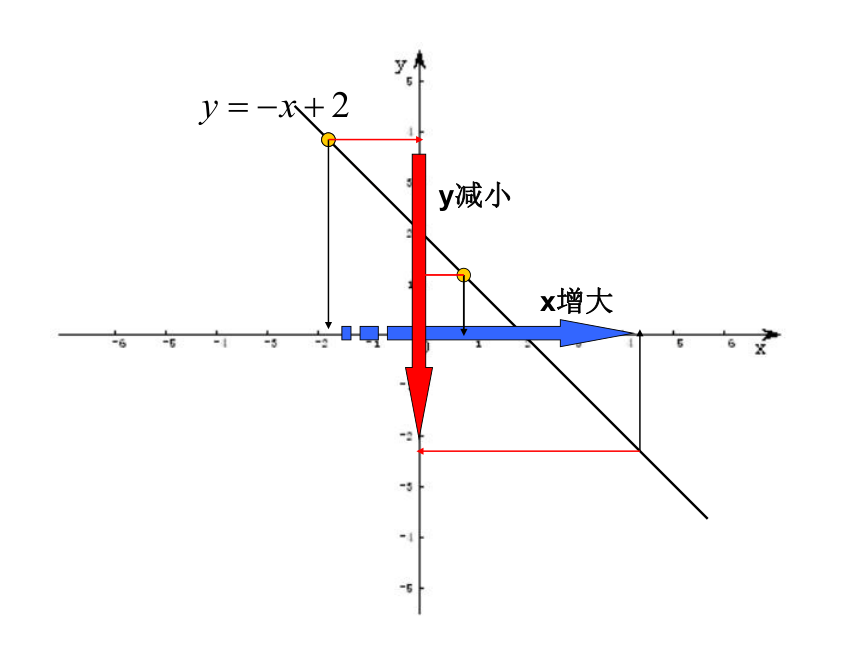
··4k<0图象呈下降趋势4x增大y增大x增大y减小一次函数y=kx+b(k≠0)有下列性质：
（1）当k>0时，y随x的增大而增大，
这时函数的图象从左到右上升；
（2）当k<0时，y随x的增大而减小，
这时函数的图象从左到右下降。知识宝典 试一试 1、下列一次函数中，y的值随x的增大而减小
的有________

(1)、(3)例1、已知函数y=(m+1)x-3
(1)当m取何值时，y随x的增大而增大？
(2)当 m取何值时，y随x的增大而减小？解：（1）当m+1>0即m>-1时y随x的增大而增大;(2)当m+1<0即m<-1时y随x的增大而减小。例2、已知点(2,m) 、(-3,n)都在直线 上，试比较 m和n的大小。你能想出几种判断的方法?
所以函数y随x增大而增大。解：方法一 把两点的坐标代入函数关系式当 x=2 时, m=当 x= -3 时, n=
所以 m > n。方法二因为 K=>0，从而直接得到 m > n。第一、三象限y随x增大
而增大 第一、二、三象限y随x增大
而增大第一、三、四象限y随x增大
而增大(0, b)(0, b)第二、四象限y随x增大
而减小第一、二、四象限y随x增大
而减小第二、三、四象限y随x增大
而减小(0, b)(o, b)1、一次函数y=kx+b中，kb>0,且y随x的增大而
减小，则它的图象大致为（ ）c达标测试 画出函数y=-2x+2的图象,结合图象回答
下列问题：
（2）当x取何值时,y=0?
（3）当x取何值时,y＞0?

做一做(2)因为 y=0 所以 -2x+2=0 ，x=1所以 当 x=1时 y=0 , 当 x＜1 时 y＞ 0；
（3）因为 y＞0 所以 -2x+2 ＞ 0 ，x < 1当x＝1时，y = 0当x < 1 时, y > 0Y>0x＜1y=-2x+23. 若函数y=(2m-1) x +m+3是一次函数，且y随着x的增大而减小，则m的值为________2-㎡4若正比例函数y=(2-m)x的图象经过点（a,b）和点（c,d），当aA.m<0 B.m>0
C.m<2 D.m>2 －1CxyY=kx+b
(k≠0)当X>-b/k时
Y>0(－b/k,0)当x=-b/k时y=0Y<0当X>-b/k时 y<0Y=kx+b(k≠0)Y>0X>-b/k(-b/k,0)Y<0X<-b/k00xy概括：对于一次函数y=kx+b(k≠0)，（1）图象与x轴交点的横坐标就是方程kx+b=0的解；
（2）图象位于x轴上方部分对应的x的取值范围就是不等式kx+b>0的解集；
（3）图象位于x轴下方部分对应的x的取值范围就是不等式kx+b< 0的解集。
小 结经过本节课的学习，你有哪些收获？教学目标掌握一次函数的性质
掌握利用一次函数的性质解决简单的函数问题
学会利用一次函数的图象解决一次方程问题、一次不等式问题