勾股定理(江西省宜春地区)

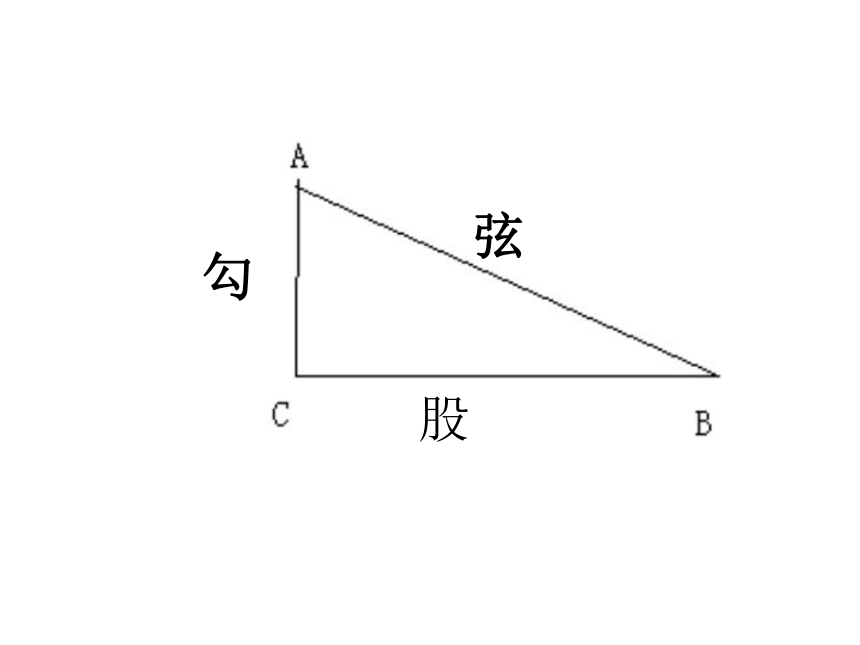
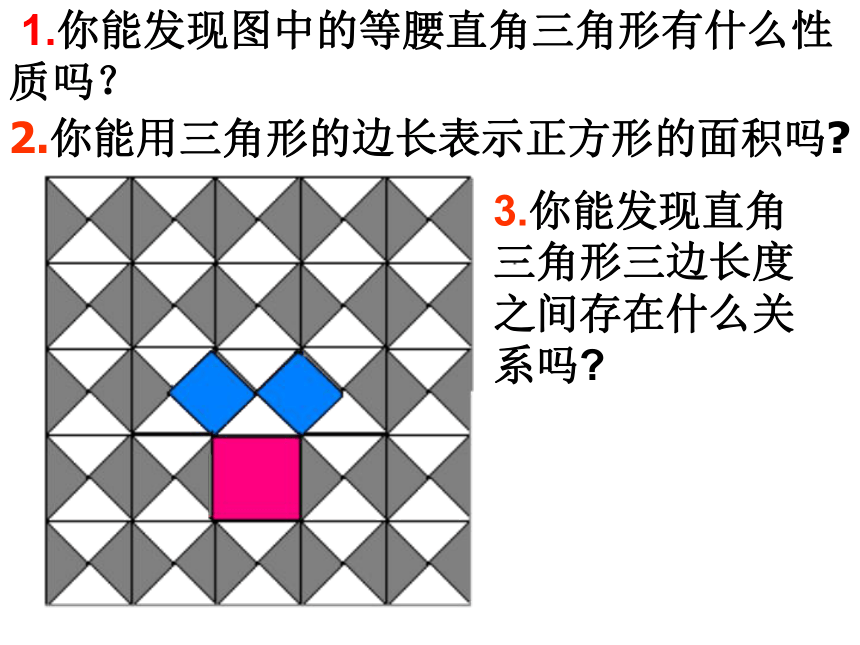
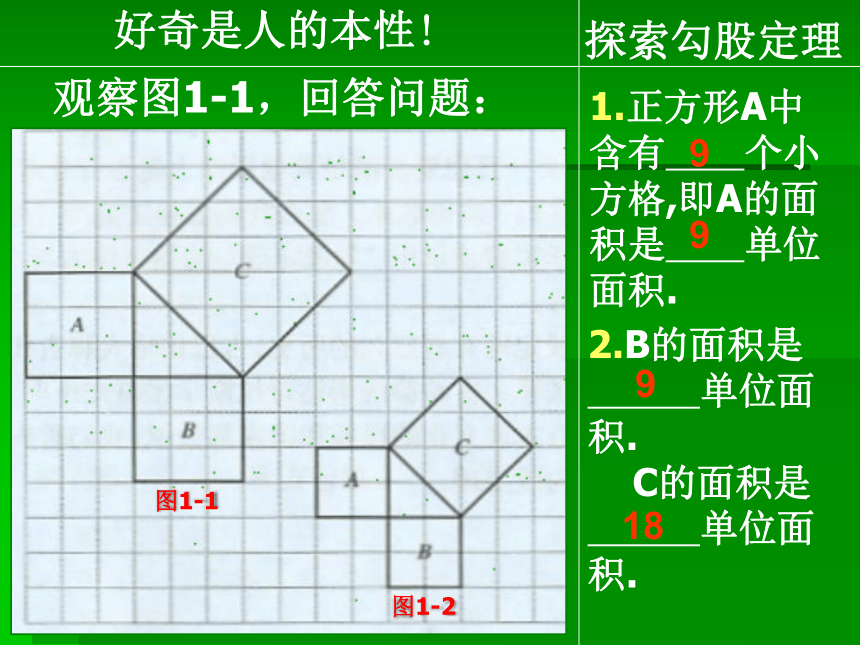
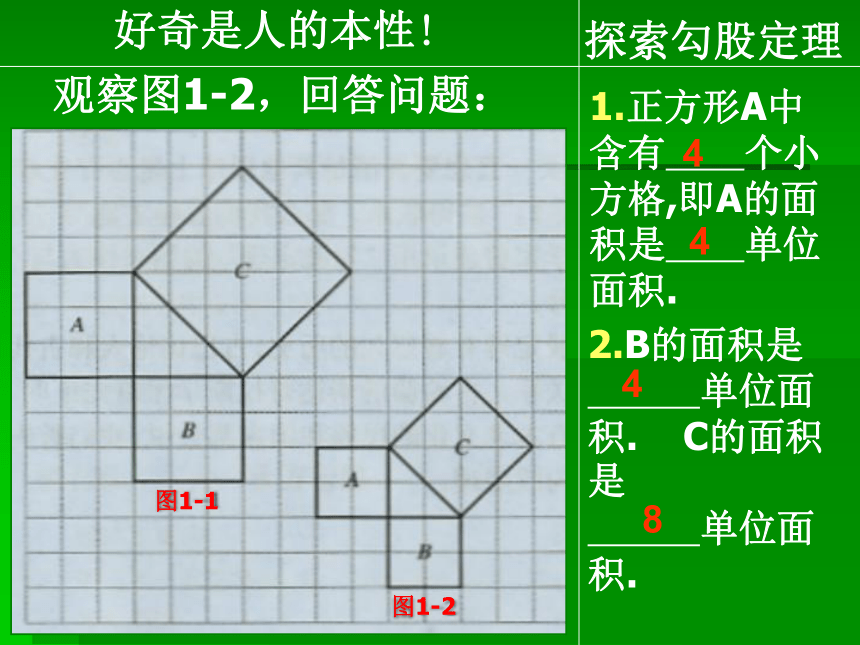
课件18张PPT。勾股定理教学目标※探索直角三角形三边关系，掌握勾股定理的运用思想，发展几何思维。※经历观察与发现直角三角形三边关系的 过程，感受勾股定理的应用意识。※培养严谨的数学学习的态度，体会勾股定理的应用价值。勾股弦 公元前572~前492年古希腊著名的哲学家、数学家、天文学家毕达哥拉斯，他在一次朋友家做客时，发现朋友家用砖铺成的地面中用了直角三角形三边的某种数量关系，请同学们一起来观察图中的地面，你能发现什么呢？ 1.你能发现图中的等腰直角三角形有什么性质吗？2.你能用三角形的边长表示正方形的面积吗?3.你能发现直角三角形三边长度之间存在什么关系吗?探索勾股定理观察图1-1，回答问题：1.正方形A中含有 个小方格,即A的面积是 单位面积.2.B的面积是 单位面积. C的面积是 单位面积.图1-1图1-2好奇是人的本性!99189探索勾股定理观察图1-2，回答问题：1.正方形A中含有 个小方格,即A的面积是 单位面积.2.B的面积是 单位面积. C的面积是 单位面积.图1-1图1-2好奇是人的本性!4448探索勾股定理观察图1-3，填表：1.正方形A中含有 个小方格,即A的面积是 单位面积.2.B的面积是 单位面积. C的面积是 单位面积.图1-3图1-4好奇是人的本性!1616925探索勾股定理观察图1-4，填表：1.正方形A中含有 个小方格,即A的面积是 单位面积.2.B的面积是 单位面积. C的面积是 单位面积.图1-3图1-4好奇是人的本性!44913命题1 如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2+b2=c2.勾股定理x 赵爽指出：按弦图，又可以勾股相乘为朱实二，倍之为朱实四，以勾股之差自相乘为中黄实。加差实，亦成弦实。赵爽弦图朱实朱实朱实C朱实⑴已知： a＝3， b＝4，求c⑵已知： c ＝10，a＝6，求b1、已知， Rt△ABC 中，a，b为的两条直角边，c为斜边，求：活学活用探究1一个门框尺寸如图所示，一块长3m，宽2.2m的薄木板能否从门框内通过？为什么？探究2ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?探索勾股定理想一想我们有:好奇是人的本性!46b=58a=4658cc2=a2+b2 =462+582
=5480 而742=5476由勾股定理得：在误差范围内1、已知：△ABC，AB＝AC＝17，BC＝16，则高AD＝＿，S△ABC＝＿. 2、池塘边有两点A、B，点C是与BA方向成直角的AC方向上一点，测得CB=60m，AC=20m。你能求出A、B两点间的距离吗？（结果保留整数）拓展延伸课堂小结⒈ 勾股定理是几何中最重要的定理之一，它揭示了直角三角形三边之间的数量关系.⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长。