4.实践与探索(2)
图片预览




文档简介
课件12张PPT。§18.5实践与探索(2) 问题创设情境 问题 画出函数y= 的图象,根据图象,指出:
(1) x取什么值时,函数值 y等于零?
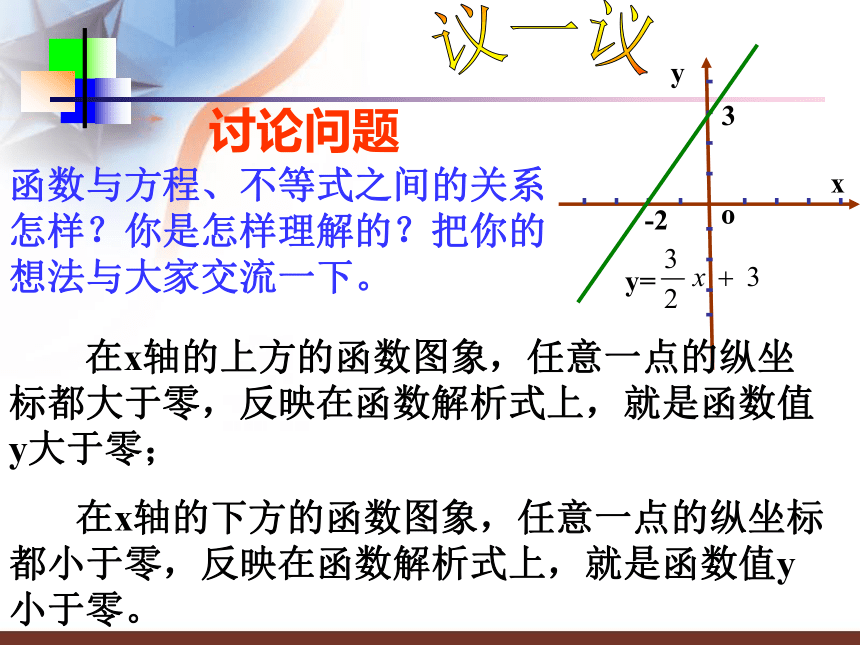
(2) x取什么值时,函数值 y始终大于零?(2)因为在x轴的上方的函数图象每一点的纵坐标都
大于0,橫坐标都 大于-2,
所以当x>-2时函数y的值大于零。解:当x=0时,y=3;
当y=0时,x=-2;
过(0,3)和(-2,0)两点作直线,就是函数 的图象从函数 的图象可以看出:因为直线 与x轴相交于点(-2,0),
所以当x=-2时,y=0,
即函数的值y等于零。做一做画出函数y=-x-2的图象,根据图象指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y始终大于零? 解 :过(-2,0),(0,-2)作直线,(1)当x=-2时,y=0;
(2)当x<-2时,y>0.议一议讨论问题函数与方程、不等式之间的关系怎样?你是怎样理解的?把你的想法与大家交流一下。 在x轴的上方的函数图象,任意一点的纵坐标都大于零,反映在函数解析式上,就是函数值y大于零;
在x轴的下方的函数图象,任意一点的纵坐标都小于零,反映在函数解析式上,就是函数值y小于零。实践运用例2 利用图象解不等式:
(1)2x-5>-x+1,
(2) 2x-5<-x+1.解:设y1=2x-5,y2=-x+1,在直角坐标系中画出这两条直线,如图.两条直线的交点坐标是(2, -1) ,可知:
(1)2x-5>-x+1即y1>y2时
x的取值范围,为x>-2;
(2)2x-5<-x+1即y1<y2时
x的取值范围,为x<-2.应用 例3如图所示,一次函数与反比例函数的图象交于A、B两点,根据图象写出使一次函数值大于反比例函数值的x的取值范围。 分析 在用图象法确定方程、不等式的解时,一是要画图准确,二是看问题全面,不能漏掉任何一种情况。检测反馈 1.已知函数y=4x-3.当x取何值时,函数的图象在第四象限?
2.画出函数y=3x-6的图象,根据图象,指出:(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y大于零?
(3) x取什么值时,函数值 y小于零?
3.画出函数y=-0.5x-1的图象,根据图象,求:(1)函数图象与x轴的交点坐标;
(2)函数图象在x轴上方时,x的取值范围;
(3)函数图象在x轴下方时,x的取值范围. 解: 从图象上看出在第二象限内,当x<-2时,一次函数的图象在反比例函数图象上方,即一次函数的值大于反比例函数的值;在第四象限内,当0<x<1时,一次函数的图象在反比例函数图象的上方,即一次函数的值,所以,当x<-2或0<x<1时,一次函数值大于反比例函数的值。交流反思 运用函数的图象来解释一元一次方程的解、一元一次不等式的解集,并能通过函数图象来回答一元一次方程的解、一元一次不等式的解集.检测反馈 4.如图,一次函数y=kx+b的图象与反比例函数 的图象交于A、B两点. (1)利用图中条件,求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y始终大于零?(2)因为在x轴的上方的函数图象每一点的纵坐标都
大于0,橫坐标都 大于-2,
所以当x>-2时函数y的值大于零。解:当x=0时,y=3;
当y=0时,x=-2;
过(0,3)和(-2,0)两点作直线,就是函数 的图象从函数 的图象可以看出:因为直线 与x轴相交于点(-2,0),
所以当x=-2时,y=0,
即函数的值y等于零。做一做画出函数y=-x-2的图象,根据图象指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y始终大于零? 解 :过(-2,0),(0,-2)作直线,(1)当x=-2时,y=0;
(2)当x<-2时,y>0.议一议讨论问题函数与方程、不等式之间的关系怎样?你是怎样理解的?把你的想法与大家交流一下。 在x轴的上方的函数图象,任意一点的纵坐标都大于零,反映在函数解析式上,就是函数值y大于零;
在x轴的下方的函数图象,任意一点的纵坐标都小于零,反映在函数解析式上,就是函数值y小于零。实践运用例2 利用图象解不等式:
(1)2x-5>-x+1,
(2) 2x-5<-x+1.解:设y1=2x-5,y2=-x+1,在直角坐标系中画出这两条直线,如图.两条直线的交点坐标是(2, -1) ,可知:
(1)2x-5>-x+1即y1>y2时
x的取值范围,为x>-2;
(2)2x-5<-x+1即y1<y2时
x的取值范围,为x<-2.应用 例3如图所示,一次函数与反比例函数的图象交于A、B两点,根据图象写出使一次函数值大于反比例函数值的x的取值范围。 分析 在用图象法确定方程、不等式的解时,一是要画图准确,二是看问题全面,不能漏掉任何一种情况。检测反馈 1.已知函数y=4x-3.当x取何值时,函数的图象在第四象限?
2.画出函数y=3x-6的图象,根据图象,指出:(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y大于零?
(3) x取什么值时,函数值 y小于零?
3.画出函数y=-0.5x-1的图象,根据图象,求:(1)函数图象与x轴的交点坐标;
(2)函数图象在x轴上方时,x的取值范围;
(3)函数图象在x轴下方时,x的取值范围. 解: 从图象上看出在第二象限内,当x<-2时,一次函数的图象在反比例函数图象上方,即一次函数的值大于反比例函数的值;在第四象限内,当0<x<1时,一次函数的图象在反比例函数图象的上方,即一次函数的值,所以,当x<-2或0<x<1时,一次函数值大于反比例函数的值。交流反思 运用函数的图象来解释一元一次方程的解、一元一次不等式的解集,并能通过函数图象来回答一元一次方程的解、一元一次不等式的解集.检测反馈 4.如图,一次函数y=kx+b的图象与反比例函数 的图象交于A、B两点. (1)利用图中条件,求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
