福建省福州市长乐区2022-2023学年八年级下学期开学考试数学试题(含答案)
文档属性
| 名称 | 福建省福州市长乐区2022-2023学年八年级下学期开学考试数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 425.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 12:55:45 | ||
图片预览



文档简介
准考证号:______ 姓名:______
(在此卷上答题无效)
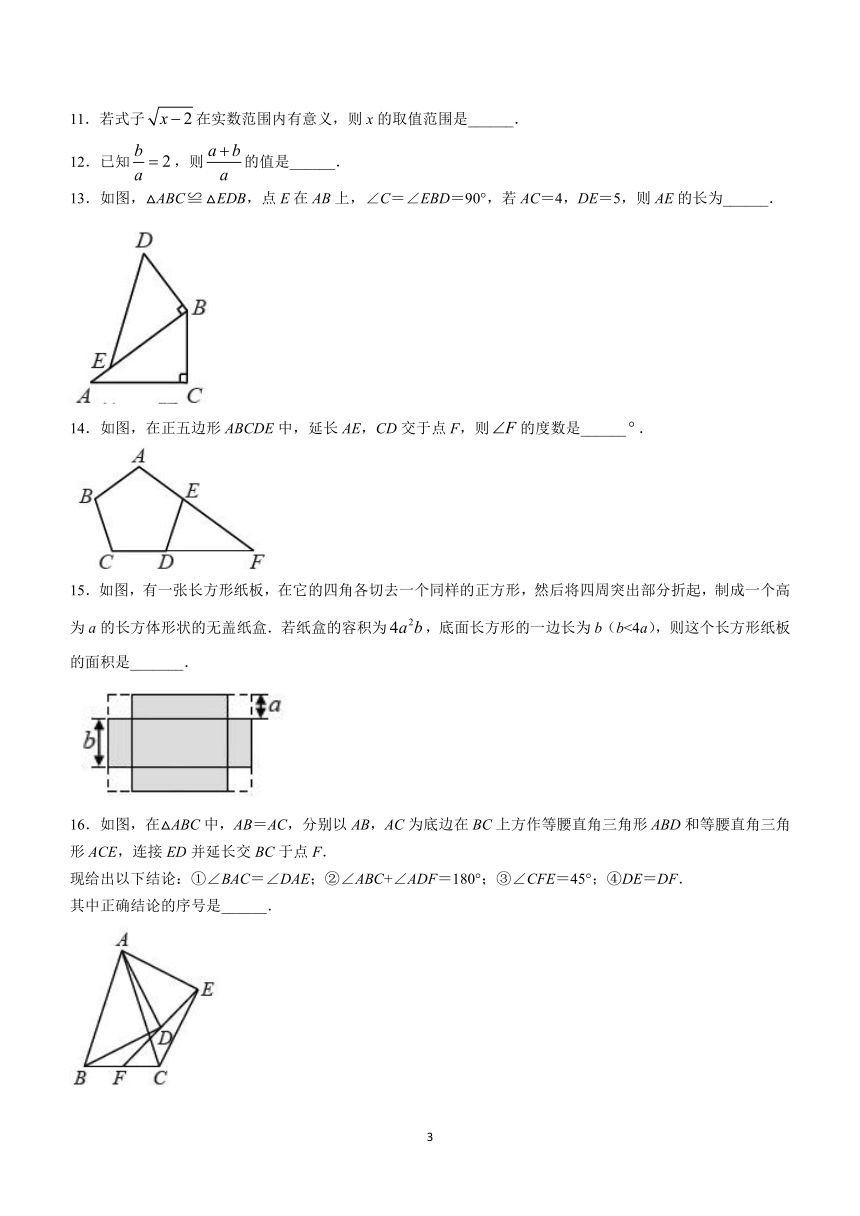
2022-2023学年第二学期开学初八年级数学
适应性练习
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,完卷时间120分钟,满分150分.
第Ⅰ卷
一、选择题(共10小题,每题4分,满分40分;每小题只有一个正确选项,请在答题卡的相应位置填涂)
1.下列图形是轴对称图形的是( )
A. B. C. D.
2.下列二次根式中,为最简二次根式的是( )
A. B. C. D.
3.我们知道,那么一把20cm的刻度尺就等于.将数据用科学记数法表示为( )
A. B. C. D.
4.下列计算结果是的是( )
A. B. C. D.
5.如图,,点D,E分别在AB,AC上,添加下列条件还不能判定△ΑBE△ACD的是( )
A. B. C. D.
6.如图,在△ABC中,,AB的垂直平分线交AB,BC于点D,E,连接AE,则下列结论错误的是( )
A. B.
C. D.
7.把分式方程去分母得到的结果正确的是( )
A. B.
C. D.
8.下列说法正确的是( )
A.三角形的外角和为180°
B.面积相等的两个三角形全等
C.等腰三角形的角平分线、中线和高相互重合
D.角的平分线上的点到角的两边的距离相等
9.如图,在中,,角平分线AD,BE相交于点F,则的度数是( )
A.130° B.135° C.140° D.145°
10.我们学了分式后,发现在中,a,b可以是整式,也可以是分式.比如:,,,也就是说具有特征的三项式,都可以写成一个代数式的平方.
问题:若添上一项M后,可以写成一个代数式的平方,则符合条件的M有( )
A.1个 B.2个 C.3个 D.超过3个
第Ⅱ卷
二、填空题(共6小题,每题4分,满分24分)
11.若式子在实数范围内有意义,则x的取值范围是______.
12.已知,则的值是______.
13.如图,△ABC△EDB,点E在AB上,∠C=∠EBD=90°,若AC=4,DE=5,则AE的长为______.
14.如图,在正五边形ABCDE中,延长AE,CD交于点F,则的度数是______.
15.如图,有一张长方形纸板,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,制成一个高为a的长方体形状的无盖纸盒.若纸盒的容积为,底面长方形的一边长为b(b<4a),则这个长方形纸板的面积是_______.
16.如图,在△ABC中,AB=AC,分别以AB,AC为底边在BC上方作等腰直角三角形ABD和等腰直角三角形ACE,连接ED并延长交BC于点F.
现给出以下结论:①∠BAC=∠DAE;②∠ABC+∠ADF=180°;③∠CFE=45°;④DE=DF.
其中正确结论的序号是______.
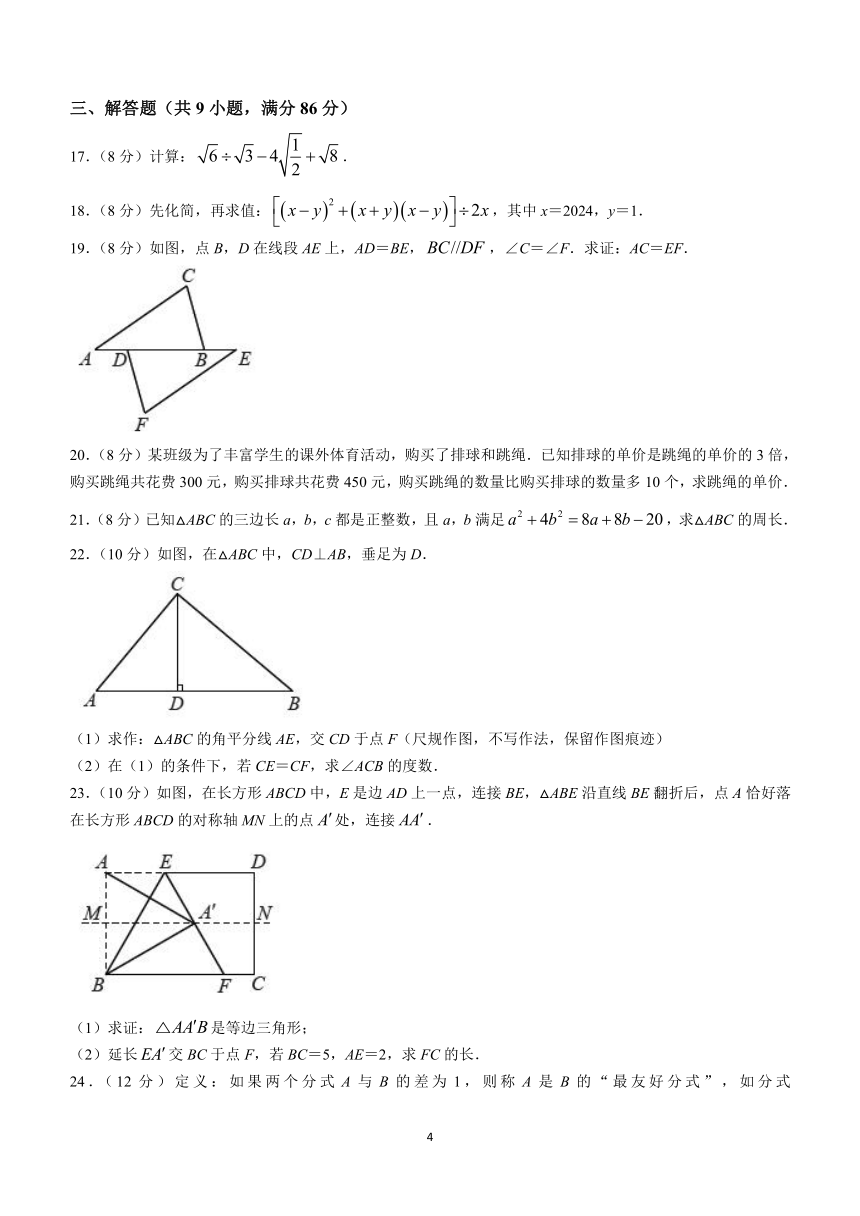
三、解答题(共9小题,满分86分)
17.(8分)计算:.
18.(8分)先化简,再求值:,其中x=2024,y=1.
19.(8分)如图,点B,D在线段AE上,AD=BE,,∠C=∠F.求证:AC=EF.
20.(8分)某班级为了丰富学生的课外体育活动,购买了排球和跳绳.已知排球的单价是跳绳的单价的3倍,购买跳绳共花费300元,购买排球共花费450元,购买跳绳的数量比购买排球的数量多10个,求跳绳的单价.
21.(8分)已知△ABC的三边长a,b,c都是正整数,且a,b满足,求△ABC的周长.
22.(10分)如图,在△ABC中,CD⊥AB,垂足为D.
(1)求作:△ABC的角平分线AE,交CD于点F(尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若CE=CF,求∠ACB的度数.
23.(10分)如图,在长方形ABCD中,E是边AD上一点,连接BE,△ABE沿直线BE翻折后,点A恰好落在长方形ABCD的对称轴MN上的点处,连接.
(1)求证:是等边三角形;
(2)延长交BC于点F,若BC=5,AE=2,求FC的长.
24.(12分)定义:如果两个分式A与B的差为1,则称A是B的“最友好分式”,如分式,则A是B的“最友好分式”.
(1)已知分式,请判断C是否为D的“最友好分式”,并说明理由;
(2)已知分式,且E是F的“最友好分式”.
①求P(用含x的式子表示);
②若为定值,求m与n之间的数量关系.
25.(14分)在△ABC中,∠ACB=90°,AC=BC,D为△ABC内一点,连接AD,BD,CD.
(1)如图1,若AC=AD,∠CAD=30°,求∠BCD的度数;
(2)如图2,若∠ADC=90°,∠CBD=∠BAD,求证:AD=2CD;
(3)如图3,在(1)的条件下,延长AD交BC于点E,P为BD上一动点,连接EP,若,,求的最小值.
2022-2023学年第二学期开学初八年级数学
适应性练习(参考答案)
一、选择题
1-5 BCDCA 6-10 BCDBD
二、填空题
11. 12.3 13.1 14.36
15. 16.①②③
三、解答题
17.解:原式
18.解:原式
当x=2024,y=1时,原式.
19.证明:∵AD=BE,∴AD+BD=BE+BD,∴AB=ED
∵,∴∠ABC=∠EDF
在△ABC和△EDF中,
∴,∴
20.解:设跳绳的单价为x元,则排球的单价为3x元,
根据题意,得,解得x=15
经检验x=15是原分式方程的解,且符合题意.
答:跳绳的单价是15元.
21.解:∵
∴
∴
∴,,解得,
∵a,b,c为△ABC的三边长,∴.
∵c是正整数,∴
∴△ABC的周长为9.
22.解:(1)如图所示,△ABC的角平分线AE,点F即为所求;
(2)∵CE=CF,∴∠CFE=∠CEF
∴AE是△ABC的角平分线,∴∠CAE=∠BAE
∵∠CFE=∠CAE+∠ACD,∠CEF=∠BAE+∠B,∴∠ACD=∠B
∵,∴∠BCD+∠B=90°
∴∠BCD+∠ACD=90°,∴∠ACB=∠BCD+∠ACD=90°.
23.(1)证明:∵直线MN是长方形ABCD的对称轴
∴MN垂直平分AB,∴
由翻折得,∴
∴是等边三角形;
(2)解:∵是等边三角形,∴
由翻折得,
在长方形ABCD中,∠BAD=∠ABC=90°
∴BE=2AE=4,,
∴∠BFE=180°-∠AEB-∠EBF=60°
∴∠BFE=∠FEB=∠EBF=60°.
∴BF=BE=4,∴FC=BC-BF=5-4=1.
24.解:(1)C是D的“最友好分式”.
理由:∵
,∴C是D的“最友好分式”;
(2)∵分式,且E是F的“最友好分式”
解得;
(3)当时,
设
∴
∴
∵为定值
∴且
由解得
把代入,得
∴.(,等关系式均可)
25.(1)解:∵AC=AD,∠CAD=30°
∴
∵∠ACB=90°
∴
(2)证明:过点B作BE⊥CD,交CD延长线于点E,则∠E=90°
∵∠ACB=90°,AC=BC
∴∠CAB=∠CBA=45°
∵∠ADC=90°,∠ACB=90°
∴∠CAD+∠ACD=∠BCD+∠ACD=90°
∴∠CAD=∠BCD
∵∠CBD=∠BAD
∴∠BDE=∠BCD+∠CBD=∠CAD+∠BAD=∠CAB=45°
∴∠BDE=∠DBE=45°
∴DE=BE.
在△ACD和△CBE中
∴
∴AD=CE,CD=BE=DE,
∴CE=CD+DE=2CD,∴AD=2CD;
(3)解:过点D作,垂足为F,G
∴∠DFC=∠ACB=∠CGD=90°
∴,∴∠FDC=∠GCD
∵DC=CD,∴,∴DF=CG
在中,
∴
∴
∴DG垂直平分BC,∴DC=DB
∴∠CBD=∠BCD=15°,
∴∠ABD=∠ABC-∠CBD=30°
过点P作,垂足为H,则
∴当点E,P,H在一条直线上时,此时,最小,
即最小,最小值为EH的长
∵,
∴
∴的最小值为
(在此卷上答题无效)
2022-2023学年第二学期开学初八年级数学
适应性练习
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,完卷时间120分钟,满分150分.
第Ⅰ卷
一、选择题(共10小题,每题4分,满分40分;每小题只有一个正确选项,请在答题卡的相应位置填涂)
1.下列图形是轴对称图形的是( )
A. B. C. D.
2.下列二次根式中,为最简二次根式的是( )
A. B. C. D.
3.我们知道,那么一把20cm的刻度尺就等于.将数据用科学记数法表示为( )
A. B. C. D.
4.下列计算结果是的是( )
A. B. C. D.
5.如图,,点D,E分别在AB,AC上,添加下列条件还不能判定△ΑBE△ACD的是( )
A. B. C. D.
6.如图,在△ABC中,,AB的垂直平分线交AB,BC于点D,E,连接AE,则下列结论错误的是( )
A. B.
C. D.
7.把分式方程去分母得到的结果正确的是( )
A. B.
C. D.
8.下列说法正确的是( )
A.三角形的外角和为180°
B.面积相等的两个三角形全等
C.等腰三角形的角平分线、中线和高相互重合
D.角的平分线上的点到角的两边的距离相等
9.如图,在中,,角平分线AD,BE相交于点F,则的度数是( )
A.130° B.135° C.140° D.145°
10.我们学了分式后,发现在中,a,b可以是整式,也可以是分式.比如:,,,也就是说具有特征的三项式,都可以写成一个代数式的平方.
问题:若添上一项M后,可以写成一个代数式的平方,则符合条件的M有( )
A.1个 B.2个 C.3个 D.超过3个
第Ⅱ卷
二、填空题(共6小题,每题4分,满分24分)
11.若式子在实数范围内有意义,则x的取值范围是______.
12.已知,则的值是______.
13.如图,△ABC△EDB,点E在AB上,∠C=∠EBD=90°,若AC=4,DE=5,则AE的长为______.
14.如图,在正五边形ABCDE中,延长AE,CD交于点F,则的度数是______.
15.如图,有一张长方形纸板,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,制成一个高为a的长方体形状的无盖纸盒.若纸盒的容积为,底面长方形的一边长为b(b<4a),则这个长方形纸板的面积是_______.
16.如图,在△ABC中,AB=AC,分别以AB,AC为底边在BC上方作等腰直角三角形ABD和等腰直角三角形ACE,连接ED并延长交BC于点F.
现给出以下结论:①∠BAC=∠DAE;②∠ABC+∠ADF=180°;③∠CFE=45°;④DE=DF.
其中正确结论的序号是______.
三、解答题(共9小题,满分86分)
17.(8分)计算:.
18.(8分)先化简,再求值:,其中x=2024,y=1.
19.(8分)如图,点B,D在线段AE上,AD=BE,,∠C=∠F.求证:AC=EF.
20.(8分)某班级为了丰富学生的课外体育活动,购买了排球和跳绳.已知排球的单价是跳绳的单价的3倍,购买跳绳共花费300元,购买排球共花费450元,购买跳绳的数量比购买排球的数量多10个,求跳绳的单价.
21.(8分)已知△ABC的三边长a,b,c都是正整数,且a,b满足,求△ABC的周长.
22.(10分)如图,在△ABC中,CD⊥AB,垂足为D.
(1)求作:△ABC的角平分线AE,交CD于点F(尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若CE=CF,求∠ACB的度数.
23.(10分)如图,在长方形ABCD中,E是边AD上一点,连接BE,△ABE沿直线BE翻折后,点A恰好落在长方形ABCD的对称轴MN上的点处,连接.
(1)求证:是等边三角形;
(2)延长交BC于点F,若BC=5,AE=2,求FC的长.
24.(12分)定义:如果两个分式A与B的差为1,则称A是B的“最友好分式”,如分式,则A是B的“最友好分式”.
(1)已知分式,请判断C是否为D的“最友好分式”,并说明理由;
(2)已知分式,且E是F的“最友好分式”.
①求P(用含x的式子表示);
②若为定值,求m与n之间的数量关系.
25.(14分)在△ABC中,∠ACB=90°,AC=BC,D为△ABC内一点,连接AD,BD,CD.
(1)如图1,若AC=AD,∠CAD=30°,求∠BCD的度数;
(2)如图2,若∠ADC=90°,∠CBD=∠BAD,求证:AD=2CD;
(3)如图3,在(1)的条件下,延长AD交BC于点E,P为BD上一动点,连接EP,若,,求的最小值.
2022-2023学年第二学期开学初八年级数学
适应性练习(参考答案)
一、选择题
1-5 BCDCA 6-10 BCDBD
二、填空题
11. 12.3 13.1 14.36
15. 16.①②③
三、解答题
17.解:原式
18.解:原式
当x=2024,y=1时,原式.
19.证明:∵AD=BE,∴AD+BD=BE+BD,∴AB=ED
∵,∴∠ABC=∠EDF
在△ABC和△EDF中,
∴,∴
20.解:设跳绳的单价为x元,则排球的单价为3x元,
根据题意,得,解得x=15
经检验x=15是原分式方程的解,且符合题意.
答:跳绳的单价是15元.
21.解:∵
∴
∴
∴,,解得,
∵a,b,c为△ABC的三边长,∴.
∵c是正整数,∴
∴△ABC的周长为9.
22.解:(1)如图所示,△ABC的角平分线AE,点F即为所求;
(2)∵CE=CF,∴∠CFE=∠CEF
∴AE是△ABC的角平分线,∴∠CAE=∠BAE
∵∠CFE=∠CAE+∠ACD,∠CEF=∠BAE+∠B,∴∠ACD=∠B
∵,∴∠BCD+∠B=90°
∴∠BCD+∠ACD=90°,∴∠ACB=∠BCD+∠ACD=90°.
23.(1)证明:∵直线MN是长方形ABCD的对称轴
∴MN垂直平分AB,∴
由翻折得,∴
∴是等边三角形;
(2)解:∵是等边三角形,∴
由翻折得,
在长方形ABCD中,∠BAD=∠ABC=90°
∴BE=2AE=4,,
∴∠BFE=180°-∠AEB-∠EBF=60°
∴∠BFE=∠FEB=∠EBF=60°.
∴BF=BE=4,∴FC=BC-BF=5-4=1.
24.解:(1)C是D的“最友好分式”.
理由:∵
,∴C是D的“最友好分式”;
(2)∵分式,且E是F的“最友好分式”
解得;
(3)当时,
设
∴
∴
∵为定值
∴且
由解得
把代入,得
∴.(,等关系式均可)
25.(1)解:∵AC=AD,∠CAD=30°
∴
∵∠ACB=90°
∴
(2)证明:过点B作BE⊥CD,交CD延长线于点E,则∠E=90°
∵∠ACB=90°,AC=BC
∴∠CAB=∠CBA=45°
∵∠ADC=90°,∠ACB=90°
∴∠CAD+∠ACD=∠BCD+∠ACD=90°
∴∠CAD=∠BCD
∵∠CBD=∠BAD
∴∠BDE=∠BCD+∠CBD=∠CAD+∠BAD=∠CAB=45°
∴∠BDE=∠DBE=45°
∴DE=BE.
在△ACD和△CBE中
∴
∴AD=CE,CD=BE=DE,
∴CE=CD+DE=2CD,∴AD=2CD;
(3)解:过点D作,垂足为F,G
∴∠DFC=∠ACB=∠CGD=90°
∴,∴∠FDC=∠GCD
∵DC=CD,∴,∴DF=CG
在中,
∴
∴
∴DG垂直平分BC,∴DC=DB
∴∠CBD=∠BCD=15°,
∴∠ABD=∠ABC-∠CBD=30°
过点P作,垂足为H,则
∴当点E,P,H在一条直线上时,此时,最小,
即最小,最小值为EH的长
∵,
∴
∴的最小值为
同课章节目录
