苏科版八年级下册物理第十章《压强和浮力》检测卷(含答案解析)
文档属性
| 名称 | 苏科版八年级下册物理第十章《压强和浮力》检测卷(含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 554.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-27 00:00:00 | ||
图片预览




文档简介
八年级下册物理单元检测卷
第十单元《压强和浮力》
班级:_________ 姓名:_________ 学号:_________
(考试时间:90分钟 试卷满分:100分)
注意事项:
1.测试范围:苏科版八年级下册第10章。
2.g=10N/kg。
3.本卷平均难度系数0.18。
第Ⅰ卷 选择题
一、选择题(本题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图所示,用F=4N的力拉着木板A做匀速直线运动从图甲到图乙,B相对地面始终保持静止。图乙中B的底面有三分之一伸出木板。已知A的质量mA=219g,A的底面积SA=30cm2,B的质量mB=81g,B的底面积SB=13.5cm2,弹簧测力计示数为1.5N。下列选项中正确的是( )
A.图甲中B所受摩擦力大小为1.5N,方向水平向左
B.图乙中B对A的压强为900Pa
C.图乙中A对地面的压强为730Pa
D.图乙中A受到地面的摩擦力大小为5.5N,方向水平向左
2.一块均匀矩形冰砖放置在水平地面上,如图甲所示,现用冰刀将冰砖的右侧切去一部分,剩余部分如图乙所示,对地面的压强p1=1800Pa;将图乙的冰砖倒置后如图丙所示,冰砖对地面的压强p2=3600Pa。甲中冰砖对地面的压强为( )
A.2100Pa B.2400Pa C.2700Pa D.3000Pa
3.两个完全相同的圆柱形容器放在水平桌面上,分别装有甲、乙两种不同的液体。将体积相同、密度不同的实心小球A、B分别放入容器中静止,A球沉底,B球漂浮,如图所示,h1<h2,且两种液体对容器底的压强相等,下列说法正确的是 ( )
①两个小球的重力:GA<GB
②两个小球的浮力:F浮A>F浮B
③两种液体的密度:ρ甲<ρ乙
④两个容器对桌面的压强:p甲>p乙
A.只有③④正确 B.只有①②正确 C.只有②④正确 D.只有①③正确
4.如图所示,圆柱体甲和装有适量某液体的圆柱形容器乙的底面积之比为3:4,把它们平放在同一水平桌面上,在甲物体上,沿水平方向截取一段长为x的物体A,并平稳放入容器乙中,用力使物体A刚好浸没在液体中(A不与容器乙接触,液体无溢出)。截取后,甲、乙对桌面的压强随截取长度x的变化关系如图丙所示。已知甲的密度为0.6×103kg/m3,容器乙的壁厚和质量均忽略不计,g取10N/kg,下列说法正确的是( )
A.圆柱体甲截取前和容器乙中的液体质量之比为3:2
B.圆柱体甲截取前对桌面的压强为1000Pa
C.容器乙中液体的密度为0.5×103 kg/m3
D.容器乙中未放入物体A时,液体的深度为7.5cm
5.如图所示,甲、乙两个均匀正方体对水平地面的压强相等。现沿水平方向在它们的上部分别切去相同的体积并将切去部分叠放在对方剩余上方的中央,则切去的部分对甲、乙剩余部分的压强Δp甲、Δp乙以及甲、乙剩余部分对地压强p甲、p乙的关系是( )
A.Δp甲>Δp乙 p甲>p乙 B.Δp甲<Δp乙 p甲<p乙
C.Δp甲>Δp乙 p甲<p乙 D.Δp甲<Δp乙 p甲>p乙
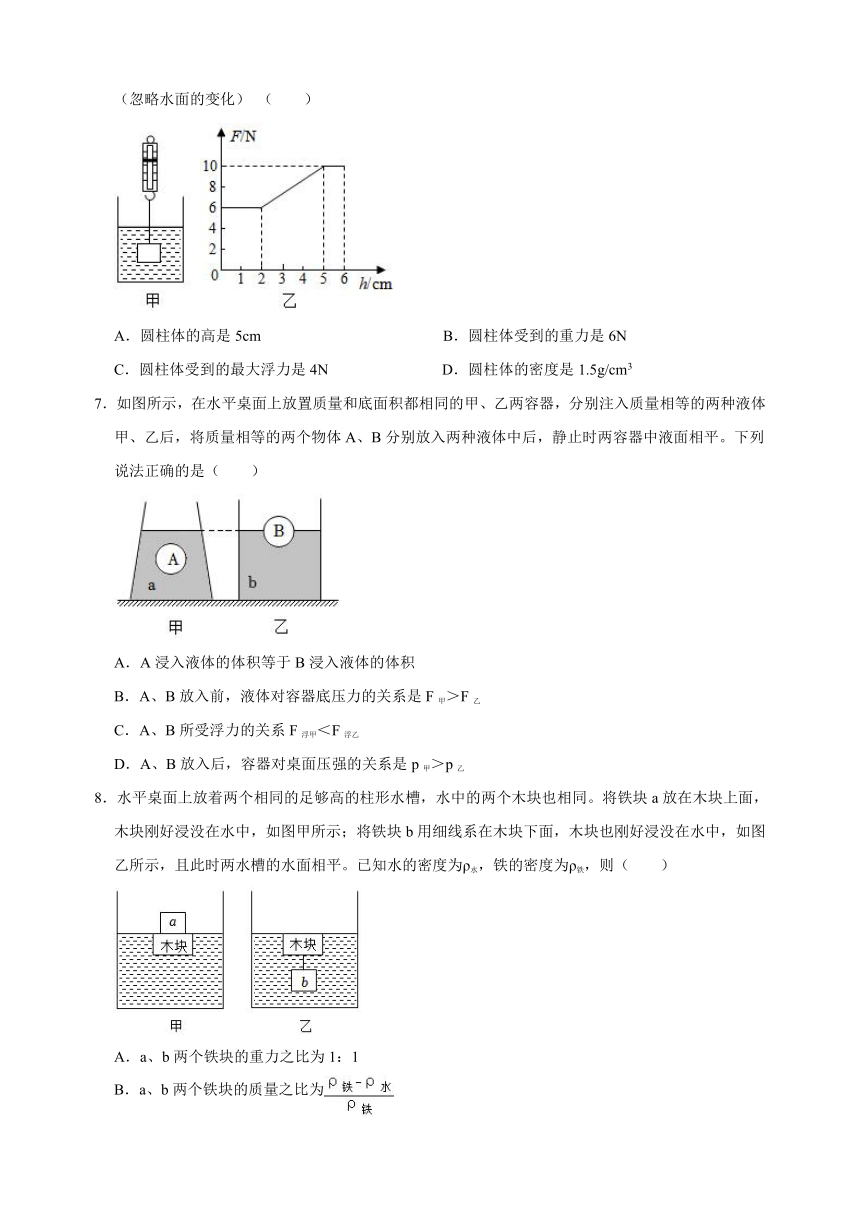
6.如图甲所示,弹簧测力计下挂有一个圆柱体,把它从盛水的烧杯中缓慢提升,直到全部露出水面,该过程中弹簧测力计读数F随圆柱体上升高度h的关系如图乙所示,下列说法正确的是(g取10N/kg)(忽略水面的变化) ( )
A.圆柱体的高是5cm B.圆柱体受到的重力是6N
C.圆柱体受到的最大浮力是4N D.圆柱体的密度是1.5g/cm3
7.如图所示,在水平桌面上放置质量和底面积都相同的甲、乙两容器,分别注入质量相等的两种液体甲、乙后,将质量相等的两个物体A、B分别放入两种液体中后,静止时两容器中液面相平。下列说法正确的是( )
A.A浸入液体的体积等于B浸入液体的体积
B.A、B放入前,液体对容器底压力的关系是F甲>F乙
C.A、B所受浮力的关系F浮甲<F浮乙
D.A、B放入后,容器对桌面压强的关系是p甲>p乙
8.水平桌面上放着两个相同的足够高的柱形水槽,水中的两个木块也相同。将铁块a放在木块上面,木块刚好浸没在水中,如图甲所示;将铁块b用细线系在木块下面,木块也刚好浸没在水中,如图乙所示,且此时两水槽的水面相平。已知水的密度为ρ水,铁的密度为ρ铁,则( )
A.a、b两个铁块的重力之比为1:1
B.a、b两个铁块的质量之比为
C.两种情况相比较,乙图中水槽对桌面的压强较大
D.若将a取下投入水中,并剪断b的细线,静止时水对容器底压强变化量Δp甲>Δp乙
9.两个质量分布均匀的正方体放在水平地面上如图甲所示,A、B对地的压强之比为4:5,将A沿水平方向切去高为L的部分,把切去部分叠放在B上,B对地面的压强为pB,A剩余部分对地的压强为pA,pA、pB与L的变化关系如图乙所示。则以下分析正确的是( )
①切除之前,A的边长为20cm
②A切除m后,余下部分的密度为4×103kg/m3
③B的底面积为400cm2
④L=2.5cm时,pA:pB=4:7
A.只有①③正确 B.只有②③正确
C.只有②④正确 D.只有②③④正确
10.放在水平桌面上的薄壁圆柱形容器(容器质量不计),底面积为10﹣3m2,将一体积为5×10﹣4m3的木块放入水中静止时,有体积露出水面,如图甲所示;用一根质量和体积不计的细线把容器底和木块底部中心连接起来,如图乙所示。下列说法(水的密度为ρ水=1.0×103kg/m3,g=10N/kg)( )
①木块的密度为0.8×103kg/m3
②木块漂浮时排开水的质量为500g
③浸没水中时细线对木块的拉力为0.8N
④甲、乙两图所示情况,容器对水平桌面的压强相等
A.只有①③正确 B.只有②③正确 C.只有①④正确 D.只有②④正确
11.如图,有A、B两个物体,用弹簧连接后置于烧杯内,再将烧杯放入装有足够多的水的容器中,静止后如图所示。已知A为正方体,重力为8N;B为体积200cm3,高4cm的柱体,重力5N;烧杯底面积为200cm2,容器底面积为250cm2,且弹簧弹力每改变1N,长度改变0.8cm。现将A、B从烧杯中取出放入水中,静止后,弹簧与图示状态相比伸长了8cm,下列说法正确的是( )
A.如图所示状态,B物体对烧杯底的压强为520Pa
B.将A、B放入水中静止后,水对烧杯底部的压强减小50Pa
C.将A、B重新放回烧杯的过程中,不小心将一些水带入烧杯中,此时水位相比于图示状态升高
D.A的密度为0.8×103kg/m3
12.如图所示装置,实心铝块(ρ铝=2.7g/cm3)B、C的体积均为10cm3,当B浸没在水中时,木块A恰能在粗糙的水平桌面上向左做匀速运动,若用铝块D替换C,则A在粗糙的桌面上向右做匀速运动,则D的质量为( )(已知水的密度为1.0×103kg/m3,铝B始终在水中,水与B之间的粘滞阻力及滑轮的摩擦均忽略不计)
A.2.7g B.7g C.4.7g D.2g
第Ⅱ卷 非选择题
二、填空题(本题共6小题,每空3分,共18分)
13.如图所示的小鸡自动喂水器主要应用_______支持瓶内的水柱,当小鸡喝水后瓶口露出时,瓶内水流出,待水面将瓶口封住时,瓶内的气压与原来瓶内的气压相比_______(选填“增大”、“减小”或“不变”)。
14.在弹簧测力计下挂一个圆柱体M,让M从盛有水的容器上方逐渐竖直浸入水中,弹簧测力计的示数F随圆柱体下表面在水中的深度h的变化关系如图所示,圆柱体刚好浸没时,下表面所受液体压强为_______Pa,圆柱体M的底面积为_______m2。(g=10N/kg,ρ水=1.0×103kg/m3)
15.如图所示,甲、乙是放在水平地面上的两个质地均匀的长方体,它们对水平地面的压强相等。已知甲、乙的高度之比h甲:h乙=3:2,底面积之比S甲:S乙=5:4,则甲、乙对地面的压力之比是_______;若将甲、乙沿竖直方向切去相同质量,并将切下部分分别叠放在对方剩余部分的上方,叠放后甲、乙对地面的压强增加量之比Δp甲:Δp乙=2:3,已知甲的质量为10kg,则甲沿竖直方向切去的质量为_______kg。
16.如图甲所示,放在水平桌面上的圆柱形容器的底面积为100cm2,装有2kg的水,容器的质量为0.2kg,厚度忽略不计。A、B是由密度不同的材料制成的两实心物块,已知B物块的体积是A物块体积的。当把A、B两物块用细线相连放入水中时,两物块恰好悬浮,且没有水溢出,如图乙所示,现剪断细线,A物块上浮,稳定后水对容器底的压强变化了60Pa,物块A有体积露出水面。则甲中容器对水平桌面的压力为_______,B物块的密度为______________。已知水的密度为1.0×103kg/m3,g取10N/kg。
17.如图所示,水平地面上放置一个质量分布均匀、底面积为100cm2的长方体甲和一个质量未知的薄壁柱形容器乙,已知容器乙的高度为20cm,其内装有3000cm3的水。现将甲沿水平方向切去一定的厚度Δh,并将甲切下的部分保持竖直轻放入乙容器的水中沉底,甲物体和乙容器对地面的压强随切去厚度Δh的变化情况如图丙所示,则Δh=10cm时,水对容器底面的压强为_______Pa;图丙中a的值为_______cm。
18.如图,圆柱体甲高50cm,底面积100cm2,质量为4kg;足够高的容器乙,底面积为200cm2,内装有10cm深的水,则此时水对乙容器底的压强为_______Pa。现将甲水平横切高度为a的部分,并将切去部分缓慢竖直放入容器乙中,此时甲剩余部分对桌面的压强与乙容器中水对容器底压强之比为2:1,则切去部分体积与圆柱体甲总体积之比为______________。
三、解答题(本题共5小题,共46分)
19.在学习浮力部分知识时萱萱想要“探究浮力的大小和哪些因素有关”,操作步骤如图1a、b、c、d、e、f。
实验步骤 b c d e f
测力计示数/N 2.4 2.3 2.2 2.2 2.0
(1)表格中缺少a的实验数据,请你根据图a读出数据: N,在实验步骤b中物体所受的浮力为_______N;
(2)分析实验步骤a、b、c、d,浸在水中的物体所受的浮力与 有关;分析_______三个实验步骤,浸没在水中的物体所受的浮力与深度_______(选填“有关”或“无关”);
(3)萱萱用表格中的数据算出了步骤f中液体的密度是_______kg/m3;
(4)同组的小春同学想用电子秤来测量矿石的密度,实验步骤如图2:
①电子秤放在水平桌面上,装有适量水的烧杯放在电子秤上,电子秤示数如图2A所示;
②把被测矿石用细线拴好,缓慢放入装有水的烧杯中,矿石未触碰到烧杯底部,电子秤的示数如图2B所示;
③然后缓慢放下矿石,让被测矿石沉入烧杯底部,如图2C所示;
根据实验步骤中的数据,可测出被测矿石的质量是_______g,被测矿石的体积_______m3,被测矿石的密度是_______kg/m3。
20.小红用菜盆盛水清洗樱桃时,将一个塑料水果盘漂浮在菜盆里的水面上盛放樱桃,当她把水里的樱桃捞起来放入果盘后,发现菜盆里的水位有所变化。为一探究竟,她用一个水槽、一个长方体空盒A、一个正方体金属块B设计了如图的实验来研究。已知水槽的底面积为200cm2,空盒A底面积为100cm2,金属块B为体积是1.25×10﹣4m3的正方体。她先把金属块B放入水槽中沉底,当空盒A漂浮在水面上时,盒底浸入水中1cm深。整个实验中,水槽里的水未溢出。(ρB=7.0×103kg/m3)
(1)空盒A漂浮在水面上时,求盒底部受到水的压强大小。
(2)求空盒A漂浮在水面上时所受浮力的大小。
(3)小红把金属块B从水中捞起后放进盒A并漂浮在水面上时,求盒A受到的浮力的大小。(金属块B上附着的水忽略不计)
(4)请计算第(3)问中水槽里的水位变化的高度。
21.如图所示,足够高的圆柱形容器A放在水平面上,内放个装满水的圆柱形容器B(B厚度不计,且与A底部未紧密贴合)。容器A底面积为300cm2,容器B质量为800g,底面积为200cm2,高度为20cm。正方体木块边长为10cm,密度为0.5g/cm3(每个木块放入容器B后会立即吸水100g),求:
(1)木块未放入水中时,容器B中的水对容器B底部的压强;
(2)把一个木块缓慢放入容器B中,当木块最终静止时,溢出的水的体积;
(3)把n个木块缓慢放入容器B中,然后全部取出,容器B能够在A中浮起时,n的最小值(不计取出木块时表面沾的水)。
22.重为2N、底面积为100cm2的薄壁圆柱形容器,盛水后放在水平桌面上。将体积分别为200cm3的木球和25cm3的塑料球用轻质细绳相连放入水中,静止时木球露出水面的体积为它自身体积的,此时容器中水的深度为20cm,如图甲所示;当把细绳剪断后,静止时木球露出水面的体积是它自身体积的,塑料球沉到容器底,如图乙所示。
(1)图甲中,水对容器底的压强是多少?
(2)木球的重力是多少?
(3)图乙中,容器底对塑料球的支持力是多少?
23.小丽同学利用一根吸管制作一个简易密度计。
(1)为了让饮料吸管能竖直的漂浮在液体中,应在吸管的 (上端/下端)塞入一些铜丝作为配重,并用石蜡将吸管的下端封闭起来。若将它放入液体中后不能竖直漂浮,请提出改进做法 。
(2)这根吸管竖直漂浮在不同液体中时,受到的浮力大小 (变大/变小/不变),液体的密度越大,它露出液面部分的长度 (越长/越短/不变)。
(3)小丽想,如果在吸管上标上相应的密度刻度,不就能直接显示所测液体密度的大小吗?于是她决定对吸管进行刻度的标定。在标定刻度前,她先测出吸管在水中漂浮时浸入水中的深度H(如图1所示)。若漂浮在密度为ρ液的其他液体中,则浸入的深度为h,可推出h的表达式为____________。(用ρ水、ρ液、H表示)根据以上表达式即可对不同液体的密度在吸管上进行标定。图2中的四种刻度的标示合理的是_________。
(4)为了使测量结果更准确,要使简易密度计上两条刻度线(如0.9、1.0)之间的距离大一些,可适当_______(选填“增大”或“减小”)配重,或换 (选填“粗”或“细”)一点的管子。
参考答案
一、选择题(本题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1、B
【分析】(1)物体B处于平衡状态,据此判断其所受摩擦力的大小;
(2)根据p===算出图乙中B对A的压强;
(3)根据p′==算出图乙中A对地面的压强;
(4)对A进行受力分析,再进一步确定地面对A的摩擦力大小和方向。
【解答】解:A、B相对地面始终保持静止,弹簧测力计的示数为1.5N,则弹簧测力计对B的拉力为1.5N,方向向左,B受到的摩擦力与拉力平衡,方向向右,大小等于1.5N,故A错误;
B、图乙中B对A的压强为:
p=====900Pa,故B正确;
C、图乙中A对地面的压强为:
p′====1000Pa,故C错误;
D、图乙中以A为研究对象,它受到向右的拉力为4N,同时受到地面对它向左的摩擦力和物体B对它向左的摩擦力,二者之和为4N,所以地面对物体A的摩擦力为4N﹣1.5N=2.5N,故D错误。
故选:B。
2、B
【分析】由F=pS算出乙、丙两图中压力,利用压力相等,求出面积比,再将乙丙组合成柱状固体,利用p=算出组合体的压强,根据柱状固体压强p======ρgh判断出图甲中砖块对水平地面的压强。
【解答】解:设图乙中砖块重力为G1,底面积为S1,图丙中砖块底面积为S2,由p=可得F=pS,可知图乙中砖块对地面压力:F1=p1S1=1800Pa×S1,图丙中砖块对地面压力:F2=p2S2=3600Pa×S2,
又因为图乙、丙中为同一砖块且均水平自然放置,砖块对地面压力:F1=F2=G1,即:1800Pa×S1=3600Pa×S2
解得:S2=S1
将乙、丙两图组装为一组合长方体,则F总=2G1,S总=S1+S2=S1
组合长方体砖块对地面的压强:p===×1800Pa=2400Pa
柱形均匀固体对水平地面的压强:p======ρgh
由于图甲和组合长方体的密度和高度均相同,所以图甲中砖块对地面的压强p'=p=2400Pa。
故选:B。
3、C
【分析】(1)由图可知,甲、乙两容器内液体的深度关系为h甲液<h乙液,因两容器中的液体对容器底的压强相等,所以,由p=ρ液gh可知两容器内液体的密度关系;
根据阿基米德原理分析两个小球受到的浮力的大小关系;根据物体的浮沉条件分析两个小球的重力的大小关系;
(2)固态对水平桌面的压力等于自身的重力;根据p=分析两个容器对桌面的压强的大小关系。
【解答】解:(1)两种液体对容器底的压强相等,且h1<h2,由p=ρ液gh可知,两种液体的密度关系为ρ甲>ρ乙,故③错误;
A小球完全浸没在甲液体中,排开甲液体的体积等于A小球的体积,B小球漂浮在乙液体中,排开乙液体的体积小于B小球的体积,因为两小球体积相等,所以两小球排开液体的体积关系为V排甲>V排乙,甲液体的密度大于乙液体的密度,由F浮=ρ液gV排可知,两个小球的浮力关系为:F浮A>F浮B,故②正确;
因为A小球在甲液体中沉底,受到的重力GA大于浮力F浮A,B小球漂浮在乙液体中,受到的重力GB等于浮力F浮B,所以两个小球的重力关系为GA>GB,故①错误;
(2)两种液体对容器底的压强相等,受力面积相等,根据F=pS可知,甲和乙两种液体对容器底的压力相等,都为F,又因为容器为柱形容器且力的作用是相互的,所以液体对容器底的压力等于液体的重力和物体受到浮力之和,即F=G液+F浮,所以甲液体的重力为:G甲=F﹣F浮A,乙液体的重力为G乙=F﹣F浮B,甲容器对桌面的压力为:F甲=G容+G甲+GA=G容+F﹣F浮A+GA,乙容器对桌面的压力为:F乙=G容+G乙+GB=G容+F﹣F浮B+GB,由于F浮B=GB,所以F乙=G容+F;
因为GA>F浮A,所以G容+F﹣F浮A+GA>G容+F,即两个容器对桌面的压力关系为F甲>F乙,由于两个容器底面积相等,由p=可知,两个容器对桌面的压强关系为p甲>p乙,故④正确。
综合分析②④正确,故C正确。
故选:C。
4、D
【分析】(1)由图像可知,截取前圆柱体甲对桌面的压强和容器乙对桌面的压强,根据p===求出圆柱体甲截取前和容器乙中的液体质量之比;
(2)设截取前圆柱体甲的高度为h,根据p=ρgh表示出圆柱体甲截取前后对桌面的压强,联立以上两式代入数据可解得圆柱体的高度,进而得出圆柱体甲截取前对桌面的压强;
(3)容器乙中未放入物体A时,根据p=p=====ρgh表示出容器乙中放入前后对桌面的压强,圆柱体甲截取长度x时,其物体A的体积VA=S甲x,联立可得容器乙中未放入物体A时液体的深度;
由B可知,p0=300Pa,根据p0=ρ乙gh乙求出容器乙中液体的密度。
【解答】解:A、由图像可知,截取前圆柱体甲对桌面的压强p甲=4p0,容器乙对桌面的压强p乙=p0,
由根据p===得,圆柱体甲截取前和容器乙中的液体质量之比:
===,故A错误;
B、设截取前圆柱体甲的高度为h,则圆柱体甲对桌面的压强:
4p0=ρ甲gh
圆柱体甲截取长度x=10cm=0.1m后,圆柱体甲对桌面的压强:
2p0=ρ甲g(h﹣x)
联立以上两式代入数据可解得:h=0.2m,所以,圆柱体甲截取前对桌面的压强:
p甲=ρ甲gh=0.6×103kg/m3×10N/kg×0.2m=1200Pa,故B错误;
CD、容器乙中未放入物体A时,对桌面的压强等于液体的压强。
即:p0=ρ乙gh乙﹣﹣﹣①
圆柱体甲截取长度x=10cm=0.1m时,则物体A的体积VA=S甲x,将物体A浸没在液体乙中,液面上升的高度:
Δh==﹣﹣﹣②
物体A刚好浸没在液体中时,容器乙对桌面的压强等于此时液体的压强
即:2p0=ρ乙g(h乙+Δh)﹣﹣﹣③
联立①②③可解得:h乙=7.5cm,故D正确;
由B可知,p0=p甲=×1200Pa=300Pa
由p0=ρ乙gh乙得,容器乙中液体的密度:
ρ乙===0.4×103kg/m3,故C错误。
故选:D。
5、A
【分析】由于两个物体都是正方体,它们各自对地面的压强相等,可利用p======ρgh先判断出两个物体的密度大小关系;
沿水平方向截去相同体积后,知道底面积关系,根据V=Sh可知截去的高度关系,知道密度关系,由沿水平方向截去相同体积ΔV后,可知切去部分的质量关系、重力关系,利用p=ρgh可得减小的压强大小关系,原来压强相等,可得剩余的物体对水平面的压强大小关系;再利用p=判断出切去的部分对甲、乙剩余部分压强的关系。
【解答】解:地面上放置的正方体物体,地面受到的压强:p======ρgh
因为两物体对水平面的压强相同,则p=ρ甲gh甲=ρ乙gh乙
由图知h甲>h乙,所以ρ甲<ρ乙;
由沿水平方向截去相同体积ΔV后,切去部分的质量为:Δm甲<Δm乙,
由G=mg可知,切去部分的重力ΔG甲<ΔG乙
已知S甲>S乙,由V=Sh可知截去的高度关系:Δh甲<Δh乙
减小的压强:Δp甲=ρ甲gΔh甲,Δp乙=ρ乙gΔh乙,则Δp甲<Δp乙
因为原来压强相等,所以将切去部分叠放在对方剩余部分上时,甲、乙剩余部分对地面压强p甲>p乙;
切去的部分对甲、乙剩余部分的压强Δp甲=,Δp乙=
因为力ΔG甲<ΔG乙,所以Δp甲>Δp乙,故A正确。故选:A。
6、C
【分析】(1)忽略水面的变化,由图乙可知,圆柱体从2cm开始露出水面到5cm完全离开水面,据此求出圆柱体的高;
(2)根据图乙可知当h>5cm时,弹簧测力计的示数为10N不变,此时圆柱体位于空中,根据二力平衡条件得出圆柱体的重力;
(3)根据图乙可知当h<2cm时,圆柱体完全浸没在水中,弹簧测力计的示数为6N不变,此时圆柱体受到的浮力最大且不变,根据称重法F浮=G﹣F′求出圆柱体受到的最大浮力;
(4)物体浸没时排开液体的体积和自身的体积相等,根据F浮=ρ液gV排求出圆柱体的体积,根据G=mg求出圆柱体的质量,利用ρ=求出圆柱体密度。
【解答】解:A.忽略水面的变化,由图乙可知,圆柱体从h1=2cm开始露出水面到h2=5cm完全离开水面,则圆柱体的高为h2﹣h1=5cm﹣2cm=3cm,故A错误;
B.由图乙可知,当h>5cm时,弹簧测力计的示数为10N不变,此时圆柱体位于空中,由二力平衡条件可知,圆柱体的重力G=F=10N,故B错误;
C.由图乙可知,当h<2cm时,圆柱体完全浸没在水中,弹簧测力计的示数为F′=6N不变,此时圆柱体受到的浮力最大且不变,
则圆柱体受到的最大浮力F浮=G﹣F′=10N﹣6N=4N,故C正确;
D.因物体浸没时排开液体的体积和自身的体积相等,所以,由F浮=ρ液gV排可得,圆柱体的体积V=V排===4×10﹣4m3
由G=mg可得,圆柱体的质量m===1kg
则圆柱体密度ρ===2.5×103kg/m3=2.5g/cm3,故D错误。
故选:C。
7、B
【分析】(1)根据容器的形状分析液体体积的大小关系,根据密度公式得出两种液体的密度的大小关系;根据物体的浮沉条件和阿基米德原理分析两个物体浸入液体中体积的大小关系;
(2)根据容器的形状分析压力与液体重力的大小关系,从而得出压力的大小关系;
(3)根据物体浮沉条件分析浮力的大小关系;
(4)水平面上的物体对水平面的压力等于自身的重力;根据p=分析容器对桌面压强的关系。
【解答】解:A.根据图乙可知,两个容器的底面积相同,两种液体的液面相平,甲容器口小底大,乙容器上下一样粗,甲容器内液体的体积小于乙容器内液体的体积,两种液体的质量相等,由ρ=可知,a液体的密度大于b液体的密度;
A全部浸入液体中,B部分浸入液体中,物体A和B的质量相等,由G=mg得到重力相等,且物体A在液体a中悬浮,物体B在液体b中漂浮,由物体沉浮条件可知,物体A受到的浮力等于A的重力,物体B受到的浮力等于B的重力,物体A受到的浮力等于物体B受到的浮力,由阿基米德原理可知A浸入液体的体积小于B浸入液体的体积,故A错误;
B.根据图示可知,甲容器口小底大,液体对容器底的压力:F甲>GA;乙容器上下一样粗,液体对容器底的压力:F乙=GB;
由于两种液体的质量相等,则GA=GB;则液体对容器底的压力的关系为:F甲>F乙,故B正确;
C.物体A和B的质量相等,由G=mg得到重力相等,且物体A在液体a中悬浮,物体B在液体b中漂浮,由物体沉浮条件可知,物体A受到的浮力等于A的重力,物体B受到的浮力等于B的重力,物体A受到的浮力等于物体B受到的浮力,故C错误;
D.根据题意可知,两个物体的质量相等,根据G=mg可知,它们的重力相等;
容器对桌面的压力等于容器、容器内液体、物体的重力总和,由于容器的质量相等,根据G=mg可知,两个容器的重力相等,液体质量相等,液体的重力相等,物体A的重力等于物体B的重力,则A、B放入后,两个容器对桌面压力相等,又因为两容器底面积相等,根据p=可知,A、B放入后容器对桌面压强相等,故D错误。故选:B。
8、B
【分析】(1)将铁块和木块看作一个整体,利用物体在液体中的浮沉条件和阿基米德原理可得出物体的密度和体积之间的关系,在密度相同时,根据ρ=可知=,从而求出质量比;利用G=mg可知重力之比;
(2)因为两水槽完全相同且水槽内水面相平,由p=ρgh可知水对容器底面的压强相等,由p=可知水对容器底面的压力相等,因为水平桌面上放着两个相同的柱形水槽,由F压=F水+G容可知容器对桌面的压力也相等;进一步可知水槽对桌面的压强关系;
(3)因为水平桌面上放着两个相同的柱形水槽,所以水对容器底的压力变化量等于排开水的重力变化量,等于木块受到的浮力变化量,根据p=可知静止时水对容器底压强变化量关系。
【解答】解:AB、甲图中,铁块a和木块一起漂浮在水面,则F浮木=Ga+G木,所以Ga=F浮木﹣G木,
即ρ铁gVa=ρ水gV木﹣ρ木gV木,乙图中,铁块b和木块一起悬浮在水中,则F浮木+F浮b=Gb+G木,
所以Gb﹣F浮b=F浮木﹣G木,即ρ铁gVb﹣ρ水gVb=ρ水gV木﹣ρ木gV木,所以ρ铁gVa=ρ铁gVb﹣ρ水gVb=(ρ铁﹣ρ水)gVb,所以=。
又因为a、b的密度相同,由m=ρV可知,a、b两个铁块的质量之比为:
==,故B正确;
利用G=mg可知a、b两个铁块的重力之比为,故A错误;
C、因为两水槽完全相同且水槽内水面相平,由p=ρgh可知水对容器底面的压强相等,由p=可知水对容器底面的压力相等,因为水平桌面上放着两个相同的柱形水槽,由F压=F水+G容可知容器对桌面的压力也相等,故图中水槽对桌面的压强相等,故C错误;
D、因为水平桌面上放着两个相同的柱形水槽,所以水对容器底的压力变化量等于排开水的重力变化量,等于木块受到的浮力变化量,将a取下投入水中,静止时,木块漂浮,a沉底,F浮木'=G木,F浮a=Ga﹣Fa,水对容器甲底的压力变化量为:ΔF压甲=ΔF浮甲=F浮木﹣(F浮木'+F浮a)=Ga+G木﹣(G木+Ga﹣Fa)=Fa,同理可得,水对容器乙底的压力变化量为:ΔF压乙=ΔF浮乙=Gb+G木﹣(F浮木'+F浮b)=Gb+G木﹣(G木+Gb﹣Fb)=Fb,又因为Fa<Fb,由Δp===可知,Δp甲<Δp乙,故D错误。
故选:B。
9、D
【分析】(1)由“将A沿水平方向切去高为L的部分,把切去部分叠放在B上”可知,A剩余部分对地的压强和B对地的压强变化,进而分析出图乙中pA、pB对应的图线;根据图乙中pA的图线变化特点求出A的边长;
(2)(3)由图乙上面的图线可知,当切去部分的高度为0cm,即A还没有被切去时,B对地的压强为5×103Pa,当切去部分的高度为10cm时,即此时A全部被叠放在B上,B对地的压强为6×103Pa,据此可列出等式,求出GB与GA的等量关系,并求出的值,进一步可解得SB和GA的值;最后利用ρ=求出A的密度;
(4)根据压强公式计算当L=2.5cm时,A对地面的压强和B对地面的压强,进一步计算pA:pB的值。
【解答】解:①由“将A沿水平方向切去高为L的部分,把切去部分叠放在B上”可知,A剩余部分对地的压强减小,B对地的压强增大,由图乙可知,下面的图线反映了pA与L的变化关系,上面的图线反映了pB与L的变化关系;由图乙中pA的图线可知,当切去部分的高度为10cm时,A剩余部分对地面的压强为0,即此时A全部被切去,因此A的边长为10cm,故①错误;
②由图乙上面的图线可知,当切去部分的高度为0cm,即A还没有被切去时,B对地的压强为5×103Pa,当切去部分的高度为10cm时,即此时A全部被叠放在B上,B对地的压强为6×103Pa,因此:
pB===5×103Pa;(1)
pB′===6×103Pa;(2)
联解(1)、(2)得:
GB=5GA;(3)
=1×103Pa;(4)
根据(3),由题意得:==×=×==;
因此SB=4SA=4×(10cm)2=400cm2=0.04m2,故③正确;
将SB=0.04m2代入(4),解得:GA=SB×1×103Pa=0.04m2×1×103Pa=40N;
则A的密度为:
ρA====4×103kg/m3;
因为密度是物质的属性,所以A切除m后,余下部分的密度仍为4×103kg/m3,故②正确;
④GB=5GA=5×40N=200N;
当L=2.5cm时,A对地面的压强为:
==3000Pa;
B对地面的压强为:
==5250Pa;
则==,故④正确。
故选:D。
10、C
【分析】(1)图甲中木块漂浮在水面上,有体积露出水面,此时受到的浮力和自身的重力相等,据此列出等式,根据阿基米德原理和G=mg=ρVg算出木块的密度;
(2)木块漂浮时,求出排开水的体积,然后根据m=ρV求出排开水的质量;
(3)甲、乙两图所示情况,容器里的水和木块仍然在容器中,总重力仍等于木块、水、容器的重力之和,总重力不变,对桌面的压力不变,根据p=判断出容器对桌面压强的变化;
(4)利用阿基米德原理求出木块浸没时受到的浮力,利用密度公式求出木块的质量,利用重力公式求出木块的重力,对木块进行受力分析可知木块受到细线的拉力大小。
【解答】解:
①木块处于漂浮状态,有体积露出水面,则V排=(1﹣)V木=V木,此时浮力等于重力,即:F浮=G,根据阿基米德原理和G=mg=ρVg得:ρ水gV木=ρ木gV木,所以,ρ木=ρ水=×1.0×103kg/m3=0.8×103kg/m3,故①正确;
②木块漂浮时,排开水的体积:V排=V木=×5×10﹣4m3=4×10﹣4m3,根据ρ=可知,排开水的质量:m排=ρ水V排=1.0×103kg/m3×4×10﹣4m3=0.4kg=400g,故②错误;
③木块浸没时,木块排开水的体积等于木块自身的体积,木块浸没时受到的浮力为F浮′=ρ水gV排′=ρ水gV木=1.0×103kg/m3×10N/kg×5×10﹣4m3=5N;
由ρ=可知,木块的质量为m木=ρ木V木=0.8×103kg/m3×5×10﹣4m3=0.4kg;
木块的重力为G=m木g=0.4kg×10N/kg=4N;
木块在浮力、重力和细线拉力的作用下保持静止,所以细线的拉力为F=F浮﹣G=5N﹣4N=1N,故③错误;
④甲、乙两图所示情况,木块和水仍然在容器中,总重力仍等于木块、水、容器的重力之和,总重力不变,对桌面的压力不变,根据p=可知,容器对水平桌面的压强相等,故④正确。
故选:C。
11、D
【分析】(1)根据B的体积和高,可求出底面积,利用p=可求出压强;
(2)根据浮沉条件、阿基米德原理、力的平衡条件求物体的体积和浮力的变化量,再由压强和密度的定义即可求解。
【解答】解:A、B的底面积为:SB===50cm2
如图所示状态,B物体对烧杯底的压强为:pB==2.6×103Pa,故A错误;
B、烧杯漂浮,浮力等于总重力,AB受到的总重力GAB=GA+GB=8N+5N=13N
将A、B放入水中静止后,弹簧与图示状态相比伸长了8cm,弹簧弹力每改变1N,长度改变0.8cm,所以弹力变化了10N;
因为原先弹簧压缩,弹力为8N,所以现在弹簧伸长,弹力为2N;
受力分析可知,A受到浮力为F浮A=2N+8N=10N;
B受到的最大浮力为:F浮B=ρ水gVB=1×103kg/m3×10N/kg×200×10﹣6m3=2N
容器为柱形容器,且原来装有A、B两物体的烧杯处于漂浮状态
则容器底受到水的压力:F1=G水+G烧杯+GAB=G水+G烧杯+13N﹣﹣﹣﹣﹣①
将A、B放入水中静止后,烧杯仍然漂浮,此时容器底受到水的压力:
F2=G水+G烧杯+F浮A+F浮B=G水+G烧杯+12N﹣﹣﹣﹣﹣②
①﹣②可得,水对容器底部的压力减小量为:ΔF=1N
水对容器底部的压强减小量为:,故B错误;
C、将一些水带入烧杯中,与开始相比浮力增大量为带入水重力,根据F浮=ρgV排,V排增大量其实就是带入水的体积,所以水位不变,故C错误;
D、由选项B的解析可知,B受浮力2N,弹力2N,重力5N,所以还受支持力1N,所以一定沉底了,所以A应该完全浸没。
由F浮=ρgV排得正方体A的体积为:
A的密度为:,故D正确;
故选:D。
12、B
【分析】要解决此题,需要掌握二力平衡条件,知道处于平衡状态的物体受平衡力的作用,一对平衡力的大小相等。
B在水中,所以受到水对它的浮力作用,所以B对A的拉力为F=G﹣F浮。
需要对物体A进行受力分析,确定两种情况下所受摩擦力的方向。根据二力平衡的条件列出两种情况下的关系式便可解决。
【解答】解:当用铝块C时,物体A向左匀速运动,所以所受摩擦力方向水平向右。
物体B在水中,受水对它向上的浮力,所以B对A的拉力FB=GB﹣F浮。
根据二力平衡条件:GC=f+GB﹣F浮
B、C是体积相同的实心铝块,所以重力相等。因此f=F浮。
若换为D,物体A向右匀速运动,所以所受摩擦力方向水平向左。
根据二力平衡条件:GD+f=GB﹣F浮,则GD=GB﹣f﹣F浮 又因为f=F浮,所以GD=GB﹣2F浮 即mDg=ρ铝VBg﹣2ρ水VBg
则mD=ρ铝VB﹣2ρ水VB=2.7g/cm3×10cm3﹣2×1g/cm3×10cm3=7g
故选:B。
二、填空题(本题共6小题,每空3分,共18分)
13.大气压;增大
【分析】小鸡自动喂水器主要应用大气压支持瓶内的水柱,当随着自动喂水的装置内水的减少,当瓶口刚露出水面时,会有少量空气进入瓶中,瓶内气压增大,瓶子的水会下降流出一部分,使水位重新升高,瓶口继续没入水中,空气不再进入,如此反复。
【解答】解:当水面刚浸没瓶口,水不再流出时,说明外界大气压等于与瓶内气压和瓶内的水压之和,因此水不再流出是大气压的作用,当瓶口露出水面,瓶内就会进入空气,水就会流出来,瓶内空气加上水的压强等于大气压,由于水的深度变小,由p=ρgh可知液体压强减小,外界大气压不变,所以瓶内气压与原来瓶内的气压相比变大。
故答案为:大气压;增大。
14.2.5×103;2.4×10﹣3
【分析】(1)由图知圆柱体M刚好浸没时下表面在水中的深度,根据p=ρgh求出此时下表面受到的液体压强;
(2)由图可知,圆柱体M下表面未进入水中时弹簧测力计的示数,即圆柱体重力;当h=25cm即圆柱体浸没时,由图可知圆柱体的高和此时弹簧测力计的示数,根据称重法求出圆柱体受到的浮力;根据阿基米德原理求出圆柱体的体积(排开水的体积),根据体积公式求出圆柱体的底面积。
【解答】解:(1)根据题意和图示可知,圆柱体刚好浸没时,圆柱体下表面在水中的深度为:h底=25cm=0.25m;
因此下表面所受液体压强:p=ρ水gh底=1.0×103kg/m3×10N/kg×0.25m=2.5×103Pa;
(2)由图可知,圆柱体M下表面未进入水中时,弹簧测力计的示数等于圆柱体重力,即:G=F=7.2N;
根据题意和图示可知,h底=25cm,圆柱体M刚好全部浸没时,弹簧测力计示数F′=1.2N,则当圆柱体M浸没时,它所受到的浮力为:
F浮=G﹣F′=7.2N﹣1.2N=6N;
由于圆柱体M刚好浸没时,则根据浮力计算公式F浮=ρgV排知物体M的体积为:
V=V排===6×10﹣4m3,
又h=25cm,圆柱体M刚好全部浸没时,圆柱体下表面在水中的深度等于圆柱体的高度,即:h=h底=25cm=0.25m;
根据V=Sh可得,圆柱体M的底面积为:
S===2.4×10﹣3m2。
故答案为:2.5×103;2.4×10﹣3。
15.5:4;4
【分析】(1)根据F=pS可求出甲、乙对地面的压力之比;
(2)在两物体上沿竖直方向截去部分的质量相等后,根据ΔS==,求出截去部分和地面的接触面积,进一步求出ΔS甲:ΔS乙;在两物体上沿竖直方向截去质量相等的部分并分别放在对方剩余部分的上方后,根据Δp=表示出甲、乙对底面的压强增加量,利用Δp甲:Δp乙=2:3和底面积关系得出ΔS甲与S甲的关系,进一步求出甲物体沿竖直方向切去的质量。
【解答】解:(1)甲、乙是放在水平地面上的两个质地均匀的长方体,它们对水平地面的压强相等,底面积之比S甲:S乙=5:4,
根据F=pS可知,甲、乙对地面的压力之比:
F甲:F乙=P甲S甲:P乙S乙=S甲:S乙=5:4;
(2)因为甲、乙是放在水平地面上的两个质地均匀的长方体,因此它们的重力等于它们对水平地面的压力,
所以G甲:G乙=F甲:F乙=5:4;
所以ρ甲:ρ乙=:=:=×=××=××=2:3;
因在两物体上沿竖直方向截去部分的质量相等,根据ΔS==可知:
==×=×=1,即:ΔS甲=ΔS乙;
在两物体上沿竖直方向截去质量相等的部分并分别放在对方剩余部分的上方后,甲、乙对底面的压强增加量分别为:
Δp甲==,Δp乙==
又因Δp甲:Δp乙=2:3,S甲:S乙=5:4
所以,3×=2×=
整理可得:ΔS甲=S甲
则甲物体沿竖直方向截去的质量:
Δm甲=ρ甲ΔV甲=ρ甲ΔS甲h甲=ρ甲×S甲h甲=m甲=×10kg=4kg。
故答案为:5:4;4。
16.22;2.5×103kg/m3;
【分析】(1)甲图中容器对桌面的压力大小就等于物体自身的重力;
(2)根据压强变化可以知道液面的变化,根据液面的变化可以求出ΔV排,ΔV排的大小就等于物体A体积的;
根据物体的漂浮原理可计算出物体A密度;
知道物体A的密度,根据物体A、B用细线相连时,处于悬浮状态,可以计算出物体B的密度。
【解答】解:(1)甲中容器对水平桌面的压力:F=G总=m总g=(m水+m容)g=(2kg+0.2kg)×10N/kg=22N;
(2)根据A物块上浮,最终漂浮,则FA浮=GA;
又因为物块A有体积露出水面可知,ρ水g×VA=ρAgVA;
则ρA=ρ水=×1.0×103kg/m3=0.75×103kg/m3;
根据水对容器底的压强变化了60Pa,根据p=ρgh可知,Δh===6×10﹣3m=0.6cm;
物体A露出水面的体积等于容器中液面下降的体积,即VA=S容Δh;
则物体A的体积:VA=4S容Δh=240cm3;
物体B的体积:VB=VA=40cm3;
物体A受到的重力:GA=ρAVAg=0.75×103kg/m3×240×10﹣6m3×10N/kg=1.8N;
把A、B两物块用细线相连放入水中时,两物块恰好悬浮可知,F浮总=ρ水g(VA+VB)=1.0×103kg/m3×10N/kg×280×10﹣6m3=2.8N;
又因为F浮总=G总=GA+GB可知,GB=F浮总﹣GA=2.8N﹣1.8N=1N;
物体B的密度:ρB====2.5×103kg/m3。
故答案为:22;2.5×103kg/m3;
17. 2×103;23。
【分析】本题比较综合,首先利用丙图获取甲的高度,计算出甲的密度;再利用甲切割10厘米,导致乙对地面的压强变化1000Pa,计算出乙的横截面积。利用水的体积及切割出来的甲的体积,算出乙的水的深度,计算出第一问水对乙容器的压强;假设切割a后利用正柱体压强公式算出甲物体对地面的压强,切割后放入乙中,导致乙压强增加量为切除甲的重力除以乙的横截面积,算出乙容器对地面的压强。利用这两个压强相等算出a的具体值。
【解答】解:由图丙知,甲物体的高度为0.4m,利用p=ρgh,得到ρ甲为2×103kg/m3;
由于甲切除的体积为V甲切=S甲×Δh=1000cm3,甲切除的重力为G甲切=ρ甲gV甲切=20N,利用乙容器对地面的压强变化了2600Pa﹣1600Pa=1000Pa,
∵S乙×1000Pa=20N,∴S乙=200cm2,Δh=10cm时,乙容器中原有的水与切下的甲物体恰填充满整个乙容器,之后水开始溢出,Δh=20cm时,此时切下来的甲物体与容器乙恰等高,因此此时水溢出达到最大,由于原来水的体积为3000cm3,放入20cm的甲物体后,剩余水的体积为V剩=(200cm2﹣100cm2)×20cm=2000m3;得溢出水的体积为ΔV=3000cm3﹣2000cm3=1000cm3;
由于水溢出,从Δh=10cm到Δh=20cm这一段中乙容器对地面产生的压强比原有应减少Δp=ρ水gΔV÷S乙=500Pa
故此时乙容器对底面的压强为p乙′=2600Pa+1000Pa﹣500Pa=3100Pa,
故Δh>20cm时,p乙的解析式为p乙=3100Pa+100(Δh﹣20)Pa﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
同时p甲=8000Pa﹣200Δh Pa﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
两图线的交点表示压强相等,即p甲=p乙
则联立①②两式可解得此时Δh=a=23cm。
故答案为:2×103;23。
18.1000;1:4。
【分析】(1)根据液体计算公式p=ρgh计算即可得出水对乙容器底的压强;
(2)根据公式V=Sh、ρ=求得圆柱体甲的密度;
若将甲水平切去一部分,并缓慢放入乙中,静止时沉底:由V=Sh可得容器中原有水此时的高度,即甲浸入水中的高度;由题意可知当切去的高度为a时,甲剩余部分对桌面的压强与乙容器中水对容器底压强之比为2:1,甲剩余部分对水平桌面的压强可表示为p甲剩=ρ甲gh剩,水对容器底部的压强为p=ρ水gh,综合可得切去的高度,进而算出切去部分体积与圆柱体甲总体积之比。
【解答】解:(1)乙容器内水的深度:h=10cm=0.1m,此时水对乙容器底的压强:
p=ρ水gh=1.0×103kg/m3×10N/kg×0.1m=1000Pa;
(2)圆柱体甲的密度:
ρ甲===0.8g/cm3=0.8×103kg/m3
若将甲水平切去一部分,并缓慢放入乙中,静止时沉底:
容器中水的高度变为:h水===0.2m,则此时甲浸入水中的高度为0.2m
圆柱体甲剩余部分对水平桌面的压强为:p甲剩=ρ甲gh剩=ρ甲g(h总﹣a)×10﹣2m=0.8×103kg/m3×10N/kg×(50﹣a)×10﹣2m=(4000﹣80a) Pa,
水对容器底部的压强:p水=ρ水gh水=1.0×103kg/m3×10N/kg×0.2m=2000Pa,由p甲剩=2p水可得:(4000﹣80a)Pa=4000Pa,故a=0cm;所以此时,故假设不成立。
(3)若将甲水平切去一部分,并缓慢放入乙中,静止时漂浮:
漂浮时物体所受浮力等于物体的重力为:F浮=Ga,即ρ甲gVa=ρ水gVa排,则===,此时甲浸入水中的深度:ha== a;
水面上升的高度为:Δh==;
甲剩余部分对水平桌面的压强:p甲剩=ρ甲gh剩=ρ甲g(h﹣a)×10﹣2m=0.8×103kg/m3×g×(50﹣a)×10﹣2m,水对容器底部的压强:p水=ρ水g(h水+Δh)=1.0×103kg/m3×g×(10+)×10﹣2m,由p甲剩=2p水可得:a=12.5cm,故假设成立。
此时切去部分体积与圆柱体甲总体积之比==12.5cm:50cm=1:4。
故答案为:1000;1:4。
三、解答题(本题共5小题,共46分)
19.(1)2.7;0.3;(2)物体排开液体的体积;a、d、e;无关;(3)1.4×103;(4)300;1.2×10﹣4;2.5×103。
【分析】(1)当物体浸在液体中时,物体所受的浮力等于物体重G减去弹簧测力计的示数F,分别计算出b、c、d浮力大小,得出随着物体浸入液体的体积(排开液体的体积)的增加,物体所受的浮力的变化情况。
(2)根据表格中数据我们可以求得图e中物体所受的浮力,与图d中物体所受浮力作比较。图d、e物体浸没在液体中,排开液体的体积相同,只是所处的深度不同,据此得出物体所受的浮力与所处的深度的关系;
(3)根据表格中数据我们可以求得图f中物体所受的浮力。图e、f两次实验中,物体排开液体的体积相同,所以我们可以根据阿基米德原理F浮=G排=ρ液gV排,列出等式求解出液体的密度;
(4)图A测量烧杯和水的总质量,图C测量烧杯、水和矿石三者的总质量,两次电子秤示数之差即为矿石的质量;B图中,矿石悬挂在细绳上,矿石受到水竖直向上的浮力,物体间力的作用是相互的,矿石给水一个竖直向下的压力作用在容器的底部,导致电子秤的示数增加,对比A图,增加的压力和浮力大小相等;
根据阿基米德原理,利用矿石的浮力求出矿石排开液体的体积,矿石的体积等于矿石排开液体的体积,然后根据密度公式求出矿石的密度。
【解答】解:
(1)由图a可知,弹簧测力计分度值为0.1N,其示数为2.7N,即物体所受的重力为2.7N。
由表可知,图b中弹簧测力计的示数为2.4N,则图b中物体所受的浮力F浮b=2.7N﹣2.4N=0.3N;
(2)同理可求得图c中物体所受的浮力为0.4N,图d中物体所受的浮力为0.5N;比较b、c、d三个图我们可以发现,随着物体浸入液体的体积(排开液体的体积)的增加,物体所受的浮力也在增加,所以我们可以得出结论:物体所受的浮力与其排开液体的体积有关,排开液体的体积越大,受到的浮力就越大;
同理可求得图e中物体所受的浮力为0.5N,与图d中物体所受浮力相等;图d、e中,物体浸没在液体中,排开液体的体积相同,只是所处的深度不同,而物体所受的浮力相同,这说明物体所受的浮力与物体所处的深度无关;
(3)根据表格中数据,图f中物体所受的浮力为F浮f=2.7N﹣2.0N=0.7N。
图e、f两次实验中,物体排开液体的体积相同,所以我们可以根据阿基米德原理列出:=;
代入数值=,可得步骤f中液体的密度为1.4×103kg/m3;
(4)由AC两图可得矿石的质量为:m石=mC﹣mA=650g﹣350g=300g=0.3kg;
B图中,矿石悬挂在细绳上,矿石受到水竖直向上的浮力,物体间力的作用是相互的,矿石给水一个竖直向下的压力作用在容器的底部,导致电子秤的示数增加,对比A图,增加的压力和浮力大小相等,
所以,矿石浸没时受到的浮力F浮=(mB﹣mA)g=(0.470kg﹣0.350kg)×10N/kg=1.2N;
根据阿基米德原理,F浮=ρ水gV排=ρ水gV石=1.0×103kg/m3×10N/kg×V石=1.2N解得V石=1.2×10﹣4m3;
矿石的密度:ρ石===2.5×103kg/m3;ρ石===2.5×103kg/m3。
故答案为:(1)2.7;0.3;(2)物体排开液体的体积;a、d、e;无关;(3)1.4×103;(4)300;1.2×10﹣4;2.5×103。
20.(1)空盒A漂浮在水面上时,盒底部受到水的压强大小为100Pa。
(2)空盒A漂浮在水面上时所受浮力的大小为1N。
(3)小红把金属块B从水中捞起后放进盒A并漂浮在水面上时,盒A受到的浮力的大小为9.75N。
(4)第(3)问中水槽里水位升高3.75cm。
【分析】(1)空盒A漂浮在水面上时,已知盒底浸入水中的深度,根据p=ρgh求出盒底部受到水的压强大小;
(2)根据V排=SAh浸算出空盒A排开水的体积,根据阿基米德原理算出空盒A受到的浮力;
(3)因物体漂浮时受到的浮力和自身的重力相等算出空盒A的重力,根据密度公式算出金属块B的质量,根据G=mg求出金属块B的重力;
把金属块B从水中捞起后放进盒A并漂浮在水面上时,根据物体漂浮条件即可求出此时盒A受到的浮力的大小;
(4)首先求出金属块B在水中时AB排开水的总体积,再根据阿基米德原理的变形公式求出A与B并漂浮在水面上时盒A排开水的体积,并求出排开水的体积的增加量,根据ΔV排=SΔh即可求出水槽里水位变化的高度。
【解答】解:(1)空盒A漂浮在水面上时,盒底浸入水中的深度h浸=1cm=1×10﹣2m,则盒底部受到水的压强:
p=ρ水gh=1.0×103kg/m3×10N/kg×1×10﹣2m=100Pa;
(2)空盒A漂浮在水面上时排开水的体积:V排=SAh浸=100cm2×1cm=100cm3=1×10﹣4m3
空盒A受到的浮力:F浮=ρ水gV排=1×103kg/m3×10N/kg×1×10﹣4m3=1N;
(3)因空盒A漂浮时受到的浮力和自身的重力相等,所以,空盒A的重力:GA=F浮=1N;
根据ρ=可得金属块B的质量:
mB=ρBVB=7.0×103kg/m3×1.25×10﹣4m3=0.875kg
则金属块B的重力:GB=mBg=0.875kg×10N/kg=8.75N
把金属块B从水中捞起后放进盒A并漂浮在水面上时,因物体漂浮时受到的浮力和自身的重力相等,
所以,此时盒A受到的浮力:F浮′=G总=GA+GB=1N+8.75N=9.75N;
(4)金属块B在水中时,AB排开水的总体积为:
V排总=V排+VB=1×10﹣4m3+1.25×10﹣4m3=2.25×10﹣4m3,金属块B从水中捞起后放进盒A,A与B漂浮在水面上时,根据F浮=ρ水gV排可得盒A排开水的体积:
V排′===9.75×10﹣4m3>2.25×10﹣4m3
即:V排′>V排总,所以,金属块B从水中捞起后放进盒A并漂浮在水面上后,水面会升高,排开水的体积的增加量:ΔV排=V排′﹣V排总=9.75×10﹣4m3﹣2.25×10﹣4m3=7.5×10﹣4m3=750cm3,则水槽里水位升高的高度:Δh===3.75cm。
答:(1)空盒A漂浮在水面上时,盒底部受到水的压强大小为100Pa。
(2)空盒A漂浮在水面上时所受浮力的大小为1N。
(3)小红把金属块B从水中捞起后放进盒A并漂浮在水面上时,盒A受到的浮力的大小为9.75N。
(4)第(3)问中水槽里水位升高3.75cm。
21.(1)木块未放入水中时,容器B中的水对容器B底部的压强为2000Pa;
(2)把一个木块缓慢放入容器B中,当木块最终静止时,溢出的水的体积为5×10﹣4m3;
(3)把n个木块缓慢放入容器B中,然后全部取出,容器B能够在A中浮起时,n的最小值为3。
【分析】(1)已知木块未放入水中时,容器B中水的深度,根据p=ρgh求水对容器B底部的压强;
(2)根据ρ=求出木块的质量,根据G=mg求木块的重力,比较木块和水的密度判断木块在水中静止时的状态,根据漂浮条件求出木块受到的浮力,根据阿基米德原理求出木块排开水的体积;
(3)当B刚好漂浮时,B所受的浮力等于剩余水和容器B的总重力,再结合阿基米德原理求得浮力,即可求出需要从B中溢出水的质量,根据漂浮条件求出木块的总重力,进而求出木块的个数。
【解答】解:
(1)木块未放入水中时,容器B中水对容器B底部的压强:
pB=ρ水ghB=1.0×103kg/m3×10N/kg×20×0.01m=2000Pa;
(2)木块的体积:V木=(10cm)3=1000cm3,由ρ=可知,木块的质量:m木=ρ木V木=0.5g/cm3×1000cm3=500g=0.5kg,木块的重力:G木=m木g=0.5kg×10N/kg=5N,若不考虑木块吸水,因为木块的密度小于水的密度,所以木块在水中最终漂浮,由物体的漂浮条件可知,木块受到的浮力:F浮=G木=5N,
由F浮=ρ水gV排可知,此时溢出水的体积为:
V溢=V排===5×10﹣4m3;
由题知,每个木块放入容器B后会立即吸水100g,吸收水的体积V吸===1×10﹣4m3,吸收水的重力G吸=m吸g=0.1kg×10N/kg=1N,吸水后木块的平均密度小于水的密度,所以木块在水中最终还是漂浮,由物体的漂浮条件可知,木块受到的浮力:F浮′=G木+G吸=5N+1N=6N,
由F浮=ρ水gV排可知,此时排开水的体积为:
V排′===6×10﹣4m3;
木块吸水后会导致水面下降,而排开水的体积增大会使得水面升高,且V排′﹣V排=V吸=1×10﹣4m3,所以可知木块吸水对溢出水的体积无影响,则溢出水的体积仍然为5×10﹣4m3;
(3)容器B中装满水时水的体积:VB=SBhB=200cm2×20cm=4000cm3,由ρ=可知,容器B中装满水时水的质量为:m水=ρ水VB=ρ水SBhB=1.0g/cm3×200cm2×20cm=4000g;
把n个木块缓慢放入容器B中,然后全部取出,则木块吸收水的总质量为m吸总=100n(g),设溢出到A容器中水的质量为m(单位为g),结合密度公式可知在容器A中水的体积为:
hA(SA﹣SB)=,则hA===cm
当容器B刚好漂浮时,B容器排开水的体积:
V排′=hASB=cm×200cm2=2m(cm3),B容器排开水的质量:m排′=ρ水V排′=1.0g/cm3×2m(cm3)=2m(单位为g),由物体的漂浮条件和阿基米德原理可知,m排′g=(mB+m水﹣100n﹣m)g,所以2m=mB+m水﹣100n﹣m=800+4000﹣100n﹣m,整理可得3m=4800﹣100n﹣﹣﹣﹣﹣﹣﹣﹣﹣①;
由(2)可知,木块吸水对溢出水的体积无影响,则每个木块溢出水的体积为5×10﹣4m3=500cm3,则n个木块溢出水的总体积V溢总=500n(cm3),所以溢出到A容器中水的质量为m=ρ水V溢总=1.0g/cm3×500n(cm3)=500n(单位为g)﹣﹣﹣﹣②
联立①②解得n=3,即需要木块的个数为3个。
答:(1)木块未放入水中时,容器B中的水对容器B底部的压强为2000Pa;
(2)把一个木块缓慢放入容器B中,当木块最终静止时,溢出的水的体积为5×10﹣4m3;
(3)把n个木块缓慢放入容器B中,然后全部取出,容器B能够在A中浮起时,n的最小值为3。
22.
(1)图甲中,水对容器底的压强是2000Pa;
(2)木球的重力是1N;
(3)图乙中,容器底对塑料球的支持力是0.25N。
【分析】(1)图甲中,知道水深和水的密度,利用p=ρgh求水对容器底的压强;
(2)由题知,当把细绳剪断后,静止时木球露出水面的体积是它自身体积的,利用F浮=G求木球的密度,利用G=mg=ρVg求木球重力;
(3)在图甲中,求出两球排开水的体积,由于木球和塑料球漂浮,受到的总浮力等于两球总重力,据此求塑料球的重力,利用阿基米德原理求塑料球在水中受到的浮力;图乙中,容器底对塑料球的支持力等于塑料球的重力减去浮力。
【解答】解:
(1)图甲中,水对容器底的压强:
p=ρ水gh=1×103kg/m3×10N/kg×0.2m=2000Pa;
(2)由题知,当把细绳剪断后,静止时木球露出水面的体积是它自身体积的,即V排=V木,
因为F浮=G,即ρ水V排g=ρ木Vg,ρ水Vg=ρ木V木g,所以ρ木=ρ水=×1×103kg/m3=0.5×103kg/m3,
木球重力:
G木=m木g=ρ木V木g=0.5×103kg/m3×10N/kg×200×10﹣6m3=1N;
(3)图甲中,两球排开水的体积V排′=(1﹣)V木+V塑=×200×10﹣6m3+25×10﹣6m3=150×10﹣6m3=1.5×10﹣4m3=150cm3,因为木球和塑料球漂浮,所以F浮′=G木+G塑,ρ水V排′g=1N+G塑
1×103kg/m3×10N/kg×1.5×10﹣4m3=1N+G塑,
则塑料球的重力:
G塑=0.5N
塑料球在水中受到的浮力:
F浮塑=ρ水V排塑g=1×103kg/m3×10N/kg×25×10﹣6m3=0.25N
图乙中,容器底对塑料球的支持力:
F支=G塑﹣F浮塑=0.5N﹣0.25N=0.25N;
答:(1)图甲中,水对容器底的压强是2000Pa;
(2)木球的重力是1N;
(3)图乙中,容器底对塑料球的支持力是0.25N。
23.见试题解答内容
【分析】(1)因为密度计是一根两端封闭即空心的,所以能使密度计浮在液体表面,为了使它保持竖直的漂浮,就在管的底部封存少许铅粒;
(2)密度计的质量一定,在液体中受力平衡,受到的浮力总是等于重力,被测液体的密度越大,排开液体的体积越小,浸入液体部分也越小,据此分析回答;
(3)根据密度计的刻度由上至下数值逐渐增大分析;
(4)为了使测量结果更准确,使密度计上两条刻度线(如0.9、1.0)之间的距离大一些,因为ΔV=sh,所以可知减小S,即可使h变大,据此设计即可。
【解答】解:
(1)为了让饮料吸管能竖直的漂浮在液体中,吸管下端塞入一些铜丝作为配重,这样做目的是让密度计竖直漂浮在液体中;若将它放入液体中后不能竖直漂浮,则可以用小钢珠作为配重;
(2)密度计是漂浮在液体中,所受浮力等于本身的重力,保持不变,如果液体的密度越大,则密度计浸入液体中的体积越小,即越往上浮,则露出液面部分的长度越长;所以密度计的刻度是越往下值越大;
(3)因为密度计是漂浮在液体中,所受浮力等于本身的重力,则F浮水=F浮液=G,即ρ水gSH=ρ液gSh=G
∵h=H,h和ρ液是反比例函数
∴刻度分布不均匀。且密度计的刻度由上至下数值逐渐增大;则密度变大时h液变化越小,故C正确;
(4)∵F浮液=G,即ρ液gSh=G,则ΔV=sh
∴ΔV变大,或使h变大,具体做法是:可适当增大配重,用更细的吸管。
故答案为:(1)下端;可以用小钢珠作为配重(重心比铜丝低的材料都可以);
(2)不变;越长;
(3)h=H;C;
(4)增大;用更细的吸管;
第十单元《压强和浮力》
班级:_________ 姓名:_________ 学号:_________
(考试时间:90分钟 试卷满分:100分)
注意事项:
1.测试范围:苏科版八年级下册第10章。
2.g=10N/kg。
3.本卷平均难度系数0.18。
第Ⅰ卷 选择题
一、选择题(本题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图所示,用F=4N的力拉着木板A做匀速直线运动从图甲到图乙,B相对地面始终保持静止。图乙中B的底面有三分之一伸出木板。已知A的质量mA=219g,A的底面积SA=30cm2,B的质量mB=81g,B的底面积SB=13.5cm2,弹簧测力计示数为1.5N。下列选项中正确的是( )
A.图甲中B所受摩擦力大小为1.5N,方向水平向左
B.图乙中B对A的压强为900Pa
C.图乙中A对地面的压强为730Pa
D.图乙中A受到地面的摩擦力大小为5.5N,方向水平向左
2.一块均匀矩形冰砖放置在水平地面上,如图甲所示,现用冰刀将冰砖的右侧切去一部分,剩余部分如图乙所示,对地面的压强p1=1800Pa;将图乙的冰砖倒置后如图丙所示,冰砖对地面的压强p2=3600Pa。甲中冰砖对地面的压强为( )
A.2100Pa B.2400Pa C.2700Pa D.3000Pa
3.两个完全相同的圆柱形容器放在水平桌面上,分别装有甲、乙两种不同的液体。将体积相同、密度不同的实心小球A、B分别放入容器中静止,A球沉底,B球漂浮,如图所示,h1<h2,且两种液体对容器底的压强相等,下列说法正确的是 ( )
①两个小球的重力:GA<GB
②两个小球的浮力:F浮A>F浮B
③两种液体的密度:ρ甲<ρ乙
④两个容器对桌面的压强:p甲>p乙
A.只有③④正确 B.只有①②正确 C.只有②④正确 D.只有①③正确
4.如图所示,圆柱体甲和装有适量某液体的圆柱形容器乙的底面积之比为3:4,把它们平放在同一水平桌面上,在甲物体上,沿水平方向截取一段长为x的物体A,并平稳放入容器乙中,用力使物体A刚好浸没在液体中(A不与容器乙接触,液体无溢出)。截取后,甲、乙对桌面的压强随截取长度x的变化关系如图丙所示。已知甲的密度为0.6×103kg/m3,容器乙的壁厚和质量均忽略不计,g取10N/kg,下列说法正确的是( )
A.圆柱体甲截取前和容器乙中的液体质量之比为3:2
B.圆柱体甲截取前对桌面的压强为1000Pa
C.容器乙中液体的密度为0.5×103 kg/m3
D.容器乙中未放入物体A时,液体的深度为7.5cm
5.如图所示,甲、乙两个均匀正方体对水平地面的压强相等。现沿水平方向在它们的上部分别切去相同的体积并将切去部分叠放在对方剩余上方的中央,则切去的部分对甲、乙剩余部分的压强Δp甲、Δp乙以及甲、乙剩余部分对地压强p甲、p乙的关系是( )
A.Δp甲>Δp乙 p甲>p乙 B.Δp甲<Δp乙 p甲<p乙
C.Δp甲>Δp乙 p甲<p乙 D.Δp甲<Δp乙 p甲>p乙
6.如图甲所示,弹簧测力计下挂有一个圆柱体,把它从盛水的烧杯中缓慢提升,直到全部露出水面,该过程中弹簧测力计读数F随圆柱体上升高度h的关系如图乙所示,下列说法正确的是(g取10N/kg)(忽略水面的变化) ( )
A.圆柱体的高是5cm B.圆柱体受到的重力是6N
C.圆柱体受到的最大浮力是4N D.圆柱体的密度是1.5g/cm3
7.如图所示,在水平桌面上放置质量和底面积都相同的甲、乙两容器,分别注入质量相等的两种液体甲、乙后,将质量相等的两个物体A、B分别放入两种液体中后,静止时两容器中液面相平。下列说法正确的是( )
A.A浸入液体的体积等于B浸入液体的体积
B.A、B放入前,液体对容器底压力的关系是F甲>F乙
C.A、B所受浮力的关系F浮甲<F浮乙
D.A、B放入后,容器对桌面压强的关系是p甲>p乙
8.水平桌面上放着两个相同的足够高的柱形水槽,水中的两个木块也相同。将铁块a放在木块上面,木块刚好浸没在水中,如图甲所示;将铁块b用细线系在木块下面,木块也刚好浸没在水中,如图乙所示,且此时两水槽的水面相平。已知水的密度为ρ水,铁的密度为ρ铁,则( )
A.a、b两个铁块的重力之比为1:1
B.a、b两个铁块的质量之比为
C.两种情况相比较,乙图中水槽对桌面的压强较大
D.若将a取下投入水中,并剪断b的细线,静止时水对容器底压强变化量Δp甲>Δp乙
9.两个质量分布均匀的正方体放在水平地面上如图甲所示,A、B对地的压强之比为4:5,将A沿水平方向切去高为L的部分,把切去部分叠放在B上,B对地面的压强为pB,A剩余部分对地的压强为pA,pA、pB与L的变化关系如图乙所示。则以下分析正确的是( )
①切除之前,A的边长为20cm
②A切除m后,余下部分的密度为4×103kg/m3
③B的底面积为400cm2
④L=2.5cm时,pA:pB=4:7
A.只有①③正确 B.只有②③正确
C.只有②④正确 D.只有②③④正确
10.放在水平桌面上的薄壁圆柱形容器(容器质量不计),底面积为10﹣3m2,将一体积为5×10﹣4m3的木块放入水中静止时,有体积露出水面,如图甲所示;用一根质量和体积不计的细线把容器底和木块底部中心连接起来,如图乙所示。下列说法(水的密度为ρ水=1.0×103kg/m3,g=10N/kg)( )
①木块的密度为0.8×103kg/m3
②木块漂浮时排开水的质量为500g
③浸没水中时细线对木块的拉力为0.8N
④甲、乙两图所示情况,容器对水平桌面的压强相等
A.只有①③正确 B.只有②③正确 C.只有①④正确 D.只有②④正确
11.如图,有A、B两个物体,用弹簧连接后置于烧杯内,再将烧杯放入装有足够多的水的容器中,静止后如图所示。已知A为正方体,重力为8N;B为体积200cm3,高4cm的柱体,重力5N;烧杯底面积为200cm2,容器底面积为250cm2,且弹簧弹力每改变1N,长度改变0.8cm。现将A、B从烧杯中取出放入水中,静止后,弹簧与图示状态相比伸长了8cm,下列说法正确的是( )
A.如图所示状态,B物体对烧杯底的压强为520Pa
B.将A、B放入水中静止后,水对烧杯底部的压强减小50Pa
C.将A、B重新放回烧杯的过程中,不小心将一些水带入烧杯中,此时水位相比于图示状态升高
D.A的密度为0.8×103kg/m3
12.如图所示装置,实心铝块(ρ铝=2.7g/cm3)B、C的体积均为10cm3,当B浸没在水中时,木块A恰能在粗糙的水平桌面上向左做匀速运动,若用铝块D替换C,则A在粗糙的桌面上向右做匀速运动,则D的质量为( )(已知水的密度为1.0×103kg/m3,铝B始终在水中,水与B之间的粘滞阻力及滑轮的摩擦均忽略不计)
A.2.7g B.7g C.4.7g D.2g
第Ⅱ卷 非选择题
二、填空题(本题共6小题,每空3分,共18分)
13.如图所示的小鸡自动喂水器主要应用_______支持瓶内的水柱,当小鸡喝水后瓶口露出时,瓶内水流出,待水面将瓶口封住时,瓶内的气压与原来瓶内的气压相比_______(选填“增大”、“减小”或“不变”)。
14.在弹簧测力计下挂一个圆柱体M,让M从盛有水的容器上方逐渐竖直浸入水中,弹簧测力计的示数F随圆柱体下表面在水中的深度h的变化关系如图所示,圆柱体刚好浸没时,下表面所受液体压强为_______Pa,圆柱体M的底面积为_______m2。(g=10N/kg,ρ水=1.0×103kg/m3)
15.如图所示,甲、乙是放在水平地面上的两个质地均匀的长方体,它们对水平地面的压强相等。已知甲、乙的高度之比h甲:h乙=3:2,底面积之比S甲:S乙=5:4,则甲、乙对地面的压力之比是_______;若将甲、乙沿竖直方向切去相同质量,并将切下部分分别叠放在对方剩余部分的上方,叠放后甲、乙对地面的压强增加量之比Δp甲:Δp乙=2:3,已知甲的质量为10kg,则甲沿竖直方向切去的质量为_______kg。
16.如图甲所示,放在水平桌面上的圆柱形容器的底面积为100cm2,装有2kg的水,容器的质量为0.2kg,厚度忽略不计。A、B是由密度不同的材料制成的两实心物块,已知B物块的体积是A物块体积的。当把A、B两物块用细线相连放入水中时,两物块恰好悬浮,且没有水溢出,如图乙所示,现剪断细线,A物块上浮,稳定后水对容器底的压强变化了60Pa,物块A有体积露出水面。则甲中容器对水平桌面的压力为_______,B物块的密度为______________。已知水的密度为1.0×103kg/m3,g取10N/kg。
17.如图所示,水平地面上放置一个质量分布均匀、底面积为100cm2的长方体甲和一个质量未知的薄壁柱形容器乙,已知容器乙的高度为20cm,其内装有3000cm3的水。现将甲沿水平方向切去一定的厚度Δh,并将甲切下的部分保持竖直轻放入乙容器的水中沉底,甲物体和乙容器对地面的压强随切去厚度Δh的变化情况如图丙所示,则Δh=10cm时,水对容器底面的压强为_______Pa;图丙中a的值为_______cm。
18.如图,圆柱体甲高50cm,底面积100cm2,质量为4kg;足够高的容器乙,底面积为200cm2,内装有10cm深的水,则此时水对乙容器底的压强为_______Pa。现将甲水平横切高度为a的部分,并将切去部分缓慢竖直放入容器乙中,此时甲剩余部分对桌面的压强与乙容器中水对容器底压强之比为2:1,则切去部分体积与圆柱体甲总体积之比为______________。
三、解答题(本题共5小题,共46分)
19.在学习浮力部分知识时萱萱想要“探究浮力的大小和哪些因素有关”,操作步骤如图1a、b、c、d、e、f。
实验步骤 b c d e f
测力计示数/N 2.4 2.3 2.2 2.2 2.0
(1)表格中缺少a的实验数据,请你根据图a读出数据: N,在实验步骤b中物体所受的浮力为_______N;
(2)分析实验步骤a、b、c、d,浸在水中的物体所受的浮力与 有关;分析_______三个实验步骤,浸没在水中的物体所受的浮力与深度_______(选填“有关”或“无关”);
(3)萱萱用表格中的数据算出了步骤f中液体的密度是_______kg/m3;
(4)同组的小春同学想用电子秤来测量矿石的密度,实验步骤如图2:
①电子秤放在水平桌面上,装有适量水的烧杯放在电子秤上,电子秤示数如图2A所示;
②把被测矿石用细线拴好,缓慢放入装有水的烧杯中,矿石未触碰到烧杯底部,电子秤的示数如图2B所示;
③然后缓慢放下矿石,让被测矿石沉入烧杯底部,如图2C所示;
根据实验步骤中的数据,可测出被测矿石的质量是_______g,被测矿石的体积_______m3,被测矿石的密度是_______kg/m3。
20.小红用菜盆盛水清洗樱桃时,将一个塑料水果盘漂浮在菜盆里的水面上盛放樱桃,当她把水里的樱桃捞起来放入果盘后,发现菜盆里的水位有所变化。为一探究竟,她用一个水槽、一个长方体空盒A、一个正方体金属块B设计了如图的实验来研究。已知水槽的底面积为200cm2,空盒A底面积为100cm2,金属块B为体积是1.25×10﹣4m3的正方体。她先把金属块B放入水槽中沉底,当空盒A漂浮在水面上时,盒底浸入水中1cm深。整个实验中,水槽里的水未溢出。(ρB=7.0×103kg/m3)
(1)空盒A漂浮在水面上时,求盒底部受到水的压强大小。
(2)求空盒A漂浮在水面上时所受浮力的大小。
(3)小红把金属块B从水中捞起后放进盒A并漂浮在水面上时,求盒A受到的浮力的大小。(金属块B上附着的水忽略不计)
(4)请计算第(3)问中水槽里的水位变化的高度。
21.如图所示,足够高的圆柱形容器A放在水平面上,内放个装满水的圆柱形容器B(B厚度不计,且与A底部未紧密贴合)。容器A底面积为300cm2,容器B质量为800g,底面积为200cm2,高度为20cm。正方体木块边长为10cm,密度为0.5g/cm3(每个木块放入容器B后会立即吸水100g),求:
(1)木块未放入水中时,容器B中的水对容器B底部的压强;
(2)把一个木块缓慢放入容器B中,当木块最终静止时,溢出的水的体积;
(3)把n个木块缓慢放入容器B中,然后全部取出,容器B能够在A中浮起时,n的最小值(不计取出木块时表面沾的水)。
22.重为2N、底面积为100cm2的薄壁圆柱形容器,盛水后放在水平桌面上。将体积分别为200cm3的木球和25cm3的塑料球用轻质细绳相连放入水中,静止时木球露出水面的体积为它自身体积的,此时容器中水的深度为20cm,如图甲所示;当把细绳剪断后,静止时木球露出水面的体积是它自身体积的,塑料球沉到容器底,如图乙所示。
(1)图甲中,水对容器底的压强是多少?
(2)木球的重力是多少?
(3)图乙中,容器底对塑料球的支持力是多少?
23.小丽同学利用一根吸管制作一个简易密度计。
(1)为了让饮料吸管能竖直的漂浮在液体中,应在吸管的 (上端/下端)塞入一些铜丝作为配重,并用石蜡将吸管的下端封闭起来。若将它放入液体中后不能竖直漂浮,请提出改进做法 。
(2)这根吸管竖直漂浮在不同液体中时,受到的浮力大小 (变大/变小/不变),液体的密度越大,它露出液面部分的长度 (越长/越短/不变)。
(3)小丽想,如果在吸管上标上相应的密度刻度,不就能直接显示所测液体密度的大小吗?于是她决定对吸管进行刻度的标定。在标定刻度前,她先测出吸管在水中漂浮时浸入水中的深度H(如图1所示)。若漂浮在密度为ρ液的其他液体中,则浸入的深度为h,可推出h的表达式为____________。(用ρ水、ρ液、H表示)根据以上表达式即可对不同液体的密度在吸管上进行标定。图2中的四种刻度的标示合理的是_________。
(4)为了使测量结果更准确,要使简易密度计上两条刻度线(如0.9、1.0)之间的距离大一些,可适当_______(选填“增大”或“减小”)配重,或换 (选填“粗”或“细”)一点的管子。
参考答案
一、选择题(本题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1、B
【分析】(1)物体B处于平衡状态,据此判断其所受摩擦力的大小;
(2)根据p===算出图乙中B对A的压强;
(3)根据p′==算出图乙中A对地面的压强;
(4)对A进行受力分析,再进一步确定地面对A的摩擦力大小和方向。
【解答】解:A、B相对地面始终保持静止,弹簧测力计的示数为1.5N,则弹簧测力计对B的拉力为1.5N,方向向左,B受到的摩擦力与拉力平衡,方向向右,大小等于1.5N,故A错误;
B、图乙中B对A的压强为:
p=====900Pa,故B正确;
C、图乙中A对地面的压强为:
p′====1000Pa,故C错误;
D、图乙中以A为研究对象,它受到向右的拉力为4N,同时受到地面对它向左的摩擦力和物体B对它向左的摩擦力,二者之和为4N,所以地面对物体A的摩擦力为4N﹣1.5N=2.5N,故D错误。
故选:B。
2、B
【分析】由F=pS算出乙、丙两图中压力,利用压力相等,求出面积比,再将乙丙组合成柱状固体,利用p=算出组合体的压强,根据柱状固体压强p======ρgh判断出图甲中砖块对水平地面的压强。
【解答】解:设图乙中砖块重力为G1,底面积为S1,图丙中砖块底面积为S2,由p=可得F=pS,可知图乙中砖块对地面压力:F1=p1S1=1800Pa×S1,图丙中砖块对地面压力:F2=p2S2=3600Pa×S2,
又因为图乙、丙中为同一砖块且均水平自然放置,砖块对地面压力:F1=F2=G1,即:1800Pa×S1=3600Pa×S2
解得:S2=S1
将乙、丙两图组装为一组合长方体,则F总=2G1,S总=S1+S2=S1
组合长方体砖块对地面的压强:p===×1800Pa=2400Pa
柱形均匀固体对水平地面的压强:p======ρgh
由于图甲和组合长方体的密度和高度均相同,所以图甲中砖块对地面的压强p'=p=2400Pa。
故选:B。
3、C
【分析】(1)由图可知,甲、乙两容器内液体的深度关系为h甲液<h乙液,因两容器中的液体对容器底的压强相等,所以,由p=ρ液gh可知两容器内液体的密度关系;
根据阿基米德原理分析两个小球受到的浮力的大小关系;根据物体的浮沉条件分析两个小球的重力的大小关系;
(2)固态对水平桌面的压力等于自身的重力;根据p=分析两个容器对桌面的压强的大小关系。
【解答】解:(1)两种液体对容器底的压强相等,且h1<h2,由p=ρ液gh可知,两种液体的密度关系为ρ甲>ρ乙,故③错误;
A小球完全浸没在甲液体中,排开甲液体的体积等于A小球的体积,B小球漂浮在乙液体中,排开乙液体的体积小于B小球的体积,因为两小球体积相等,所以两小球排开液体的体积关系为V排甲>V排乙,甲液体的密度大于乙液体的密度,由F浮=ρ液gV排可知,两个小球的浮力关系为:F浮A>F浮B,故②正确;
因为A小球在甲液体中沉底,受到的重力GA大于浮力F浮A,B小球漂浮在乙液体中,受到的重力GB等于浮力F浮B,所以两个小球的重力关系为GA>GB,故①错误;
(2)两种液体对容器底的压强相等,受力面积相等,根据F=pS可知,甲和乙两种液体对容器底的压力相等,都为F,又因为容器为柱形容器且力的作用是相互的,所以液体对容器底的压力等于液体的重力和物体受到浮力之和,即F=G液+F浮,所以甲液体的重力为:G甲=F﹣F浮A,乙液体的重力为G乙=F﹣F浮B,甲容器对桌面的压力为:F甲=G容+G甲+GA=G容+F﹣F浮A+GA,乙容器对桌面的压力为:F乙=G容+G乙+GB=G容+F﹣F浮B+GB,由于F浮B=GB,所以F乙=G容+F;
因为GA>F浮A,所以G容+F﹣F浮A+GA>G容+F,即两个容器对桌面的压力关系为F甲>F乙,由于两个容器底面积相等,由p=可知,两个容器对桌面的压强关系为p甲>p乙,故④正确。
综合分析②④正确,故C正确。
故选:C。
4、D
【分析】(1)由图像可知,截取前圆柱体甲对桌面的压强和容器乙对桌面的压强,根据p===求出圆柱体甲截取前和容器乙中的液体质量之比;
(2)设截取前圆柱体甲的高度为h,根据p=ρgh表示出圆柱体甲截取前后对桌面的压强,联立以上两式代入数据可解得圆柱体的高度,进而得出圆柱体甲截取前对桌面的压强;
(3)容器乙中未放入物体A时,根据p=p=====ρgh表示出容器乙中放入前后对桌面的压强,圆柱体甲截取长度x时,其物体A的体积VA=S甲x,联立可得容器乙中未放入物体A时液体的深度;
由B可知,p0=300Pa,根据p0=ρ乙gh乙求出容器乙中液体的密度。
【解答】解:A、由图像可知,截取前圆柱体甲对桌面的压强p甲=4p0,容器乙对桌面的压强p乙=p0,
由根据p===得,圆柱体甲截取前和容器乙中的液体质量之比:
===,故A错误;
B、设截取前圆柱体甲的高度为h,则圆柱体甲对桌面的压强:
4p0=ρ甲gh
圆柱体甲截取长度x=10cm=0.1m后,圆柱体甲对桌面的压强:
2p0=ρ甲g(h﹣x)
联立以上两式代入数据可解得:h=0.2m,所以,圆柱体甲截取前对桌面的压强:
p甲=ρ甲gh=0.6×103kg/m3×10N/kg×0.2m=1200Pa,故B错误;
CD、容器乙中未放入物体A时,对桌面的压强等于液体的压强。
即:p0=ρ乙gh乙﹣﹣﹣①
圆柱体甲截取长度x=10cm=0.1m时,则物体A的体积VA=S甲x,将物体A浸没在液体乙中,液面上升的高度:
Δh==﹣﹣﹣②
物体A刚好浸没在液体中时,容器乙对桌面的压强等于此时液体的压强
即:2p0=ρ乙g(h乙+Δh)﹣﹣﹣③
联立①②③可解得:h乙=7.5cm,故D正确;
由B可知,p0=p甲=×1200Pa=300Pa
由p0=ρ乙gh乙得,容器乙中液体的密度:
ρ乙===0.4×103kg/m3,故C错误。
故选:D。
5、A
【分析】由于两个物体都是正方体,它们各自对地面的压强相等,可利用p======ρgh先判断出两个物体的密度大小关系;
沿水平方向截去相同体积后,知道底面积关系,根据V=Sh可知截去的高度关系,知道密度关系,由沿水平方向截去相同体积ΔV后,可知切去部分的质量关系、重力关系,利用p=ρgh可得减小的压强大小关系,原来压强相等,可得剩余的物体对水平面的压强大小关系;再利用p=判断出切去的部分对甲、乙剩余部分压强的关系。
【解答】解:地面上放置的正方体物体,地面受到的压强:p======ρgh
因为两物体对水平面的压强相同,则p=ρ甲gh甲=ρ乙gh乙
由图知h甲>h乙,所以ρ甲<ρ乙;
由沿水平方向截去相同体积ΔV后,切去部分的质量为:Δm甲<Δm乙,
由G=mg可知,切去部分的重力ΔG甲<ΔG乙
已知S甲>S乙,由V=Sh可知截去的高度关系:Δh甲<Δh乙
减小的压强:Δp甲=ρ甲gΔh甲,Δp乙=ρ乙gΔh乙,则Δp甲<Δp乙
因为原来压强相等,所以将切去部分叠放在对方剩余部分上时,甲、乙剩余部分对地面压强p甲>p乙;
切去的部分对甲、乙剩余部分的压强Δp甲=,Δp乙=
因为力ΔG甲<ΔG乙,所以Δp甲>Δp乙,故A正确。故选:A。
6、C
【分析】(1)忽略水面的变化,由图乙可知,圆柱体从2cm开始露出水面到5cm完全离开水面,据此求出圆柱体的高;
(2)根据图乙可知当h>5cm时,弹簧测力计的示数为10N不变,此时圆柱体位于空中,根据二力平衡条件得出圆柱体的重力;
(3)根据图乙可知当h<2cm时,圆柱体完全浸没在水中,弹簧测力计的示数为6N不变,此时圆柱体受到的浮力最大且不变,根据称重法F浮=G﹣F′求出圆柱体受到的最大浮力;
(4)物体浸没时排开液体的体积和自身的体积相等,根据F浮=ρ液gV排求出圆柱体的体积,根据G=mg求出圆柱体的质量,利用ρ=求出圆柱体密度。
【解答】解:A.忽略水面的变化,由图乙可知,圆柱体从h1=2cm开始露出水面到h2=5cm完全离开水面,则圆柱体的高为h2﹣h1=5cm﹣2cm=3cm,故A错误;
B.由图乙可知,当h>5cm时,弹簧测力计的示数为10N不变,此时圆柱体位于空中,由二力平衡条件可知,圆柱体的重力G=F=10N,故B错误;
C.由图乙可知,当h<2cm时,圆柱体完全浸没在水中,弹簧测力计的示数为F′=6N不变,此时圆柱体受到的浮力最大且不变,
则圆柱体受到的最大浮力F浮=G﹣F′=10N﹣6N=4N,故C正确;
D.因物体浸没时排开液体的体积和自身的体积相等,所以,由F浮=ρ液gV排可得,圆柱体的体积V=V排===4×10﹣4m3
由G=mg可得,圆柱体的质量m===1kg
则圆柱体密度ρ===2.5×103kg/m3=2.5g/cm3,故D错误。
故选:C。
7、B
【分析】(1)根据容器的形状分析液体体积的大小关系,根据密度公式得出两种液体的密度的大小关系;根据物体的浮沉条件和阿基米德原理分析两个物体浸入液体中体积的大小关系;
(2)根据容器的形状分析压力与液体重力的大小关系,从而得出压力的大小关系;
(3)根据物体浮沉条件分析浮力的大小关系;
(4)水平面上的物体对水平面的压力等于自身的重力;根据p=分析容器对桌面压强的关系。
【解答】解:A.根据图乙可知,两个容器的底面积相同,两种液体的液面相平,甲容器口小底大,乙容器上下一样粗,甲容器内液体的体积小于乙容器内液体的体积,两种液体的质量相等,由ρ=可知,a液体的密度大于b液体的密度;
A全部浸入液体中,B部分浸入液体中,物体A和B的质量相等,由G=mg得到重力相等,且物体A在液体a中悬浮,物体B在液体b中漂浮,由物体沉浮条件可知,物体A受到的浮力等于A的重力,物体B受到的浮力等于B的重力,物体A受到的浮力等于物体B受到的浮力,由阿基米德原理可知A浸入液体的体积小于B浸入液体的体积,故A错误;
B.根据图示可知,甲容器口小底大,液体对容器底的压力:F甲>GA;乙容器上下一样粗,液体对容器底的压力:F乙=GB;
由于两种液体的质量相等,则GA=GB;则液体对容器底的压力的关系为:F甲>F乙,故B正确;
C.物体A和B的质量相等,由G=mg得到重力相等,且物体A在液体a中悬浮,物体B在液体b中漂浮,由物体沉浮条件可知,物体A受到的浮力等于A的重力,物体B受到的浮力等于B的重力,物体A受到的浮力等于物体B受到的浮力,故C错误;
D.根据题意可知,两个物体的质量相等,根据G=mg可知,它们的重力相等;
容器对桌面的压力等于容器、容器内液体、物体的重力总和,由于容器的质量相等,根据G=mg可知,两个容器的重力相等,液体质量相等,液体的重力相等,物体A的重力等于物体B的重力,则A、B放入后,两个容器对桌面压力相等,又因为两容器底面积相等,根据p=可知,A、B放入后容器对桌面压强相等,故D错误。故选:B。
8、B
【分析】(1)将铁块和木块看作一个整体,利用物体在液体中的浮沉条件和阿基米德原理可得出物体的密度和体积之间的关系,在密度相同时,根据ρ=可知=,从而求出质量比;利用G=mg可知重力之比;
(2)因为两水槽完全相同且水槽内水面相平,由p=ρgh可知水对容器底面的压强相等,由p=可知水对容器底面的压力相等,因为水平桌面上放着两个相同的柱形水槽,由F压=F水+G容可知容器对桌面的压力也相等;进一步可知水槽对桌面的压强关系;
(3)因为水平桌面上放着两个相同的柱形水槽,所以水对容器底的压力变化量等于排开水的重力变化量,等于木块受到的浮力变化量,根据p=可知静止时水对容器底压强变化量关系。
【解答】解:AB、甲图中,铁块a和木块一起漂浮在水面,则F浮木=Ga+G木,所以Ga=F浮木﹣G木,
即ρ铁gVa=ρ水gV木﹣ρ木gV木,乙图中,铁块b和木块一起悬浮在水中,则F浮木+F浮b=Gb+G木,
所以Gb﹣F浮b=F浮木﹣G木,即ρ铁gVb﹣ρ水gVb=ρ水gV木﹣ρ木gV木,所以ρ铁gVa=ρ铁gVb﹣ρ水gVb=(ρ铁﹣ρ水)gVb,所以=。
又因为a、b的密度相同,由m=ρV可知,a、b两个铁块的质量之比为:
==,故B正确;
利用G=mg可知a、b两个铁块的重力之比为,故A错误;
C、因为两水槽完全相同且水槽内水面相平,由p=ρgh可知水对容器底面的压强相等,由p=可知水对容器底面的压力相等,因为水平桌面上放着两个相同的柱形水槽,由F压=F水+G容可知容器对桌面的压力也相等,故图中水槽对桌面的压强相等,故C错误;
D、因为水平桌面上放着两个相同的柱形水槽,所以水对容器底的压力变化量等于排开水的重力变化量,等于木块受到的浮力变化量,将a取下投入水中,静止时,木块漂浮,a沉底,F浮木'=G木,F浮a=Ga﹣Fa,水对容器甲底的压力变化量为:ΔF压甲=ΔF浮甲=F浮木﹣(F浮木'+F浮a)=Ga+G木﹣(G木+Ga﹣Fa)=Fa,同理可得,水对容器乙底的压力变化量为:ΔF压乙=ΔF浮乙=Gb+G木﹣(F浮木'+F浮b)=Gb+G木﹣(G木+Gb﹣Fb)=Fb,又因为Fa<Fb,由Δp===可知,Δp甲<Δp乙,故D错误。
故选:B。
9、D
【分析】(1)由“将A沿水平方向切去高为L的部分,把切去部分叠放在B上”可知,A剩余部分对地的压强和B对地的压强变化,进而分析出图乙中pA、pB对应的图线;根据图乙中pA的图线变化特点求出A的边长;
(2)(3)由图乙上面的图线可知,当切去部分的高度为0cm,即A还没有被切去时,B对地的压强为5×103Pa,当切去部分的高度为10cm时,即此时A全部被叠放在B上,B对地的压强为6×103Pa,据此可列出等式,求出GB与GA的等量关系,并求出的值,进一步可解得SB和GA的值;最后利用ρ=求出A的密度;
(4)根据压强公式计算当L=2.5cm时,A对地面的压强和B对地面的压强,进一步计算pA:pB的值。
【解答】解:①由“将A沿水平方向切去高为L的部分,把切去部分叠放在B上”可知,A剩余部分对地的压强减小,B对地的压强增大,由图乙可知,下面的图线反映了pA与L的变化关系,上面的图线反映了pB与L的变化关系;由图乙中pA的图线可知,当切去部分的高度为10cm时,A剩余部分对地面的压强为0,即此时A全部被切去,因此A的边长为10cm,故①错误;
②由图乙上面的图线可知,当切去部分的高度为0cm,即A还没有被切去时,B对地的压强为5×103Pa,当切去部分的高度为10cm时,即此时A全部被叠放在B上,B对地的压强为6×103Pa,因此:
pB===5×103Pa;(1)
pB′===6×103Pa;(2)
联解(1)、(2)得:
GB=5GA;(3)
=1×103Pa;(4)
根据(3),由题意得:==×=×==;
因此SB=4SA=4×(10cm)2=400cm2=0.04m2,故③正确;
将SB=0.04m2代入(4),解得:GA=SB×1×103Pa=0.04m2×1×103Pa=40N;
则A的密度为:
ρA====4×103kg/m3;
因为密度是物质的属性,所以A切除m后,余下部分的密度仍为4×103kg/m3,故②正确;
④GB=5GA=5×40N=200N;
当L=2.5cm时,A对地面的压强为:
==3000Pa;
B对地面的压强为:
==5250Pa;
则==,故④正确。
故选:D。
10、C
【分析】(1)图甲中木块漂浮在水面上,有体积露出水面,此时受到的浮力和自身的重力相等,据此列出等式,根据阿基米德原理和G=mg=ρVg算出木块的密度;
(2)木块漂浮时,求出排开水的体积,然后根据m=ρV求出排开水的质量;
(3)甲、乙两图所示情况,容器里的水和木块仍然在容器中,总重力仍等于木块、水、容器的重力之和,总重力不变,对桌面的压力不变,根据p=判断出容器对桌面压强的变化;
(4)利用阿基米德原理求出木块浸没时受到的浮力,利用密度公式求出木块的质量,利用重力公式求出木块的重力,对木块进行受力分析可知木块受到细线的拉力大小。
【解答】解:
①木块处于漂浮状态,有体积露出水面,则V排=(1﹣)V木=V木,此时浮力等于重力,即:F浮=G,根据阿基米德原理和G=mg=ρVg得:ρ水gV木=ρ木gV木,所以,ρ木=ρ水=×1.0×103kg/m3=0.8×103kg/m3,故①正确;
②木块漂浮时,排开水的体积:V排=V木=×5×10﹣4m3=4×10﹣4m3,根据ρ=可知,排开水的质量:m排=ρ水V排=1.0×103kg/m3×4×10﹣4m3=0.4kg=400g,故②错误;
③木块浸没时,木块排开水的体积等于木块自身的体积,木块浸没时受到的浮力为F浮′=ρ水gV排′=ρ水gV木=1.0×103kg/m3×10N/kg×5×10﹣4m3=5N;
由ρ=可知,木块的质量为m木=ρ木V木=0.8×103kg/m3×5×10﹣4m3=0.4kg;
木块的重力为G=m木g=0.4kg×10N/kg=4N;
木块在浮力、重力和细线拉力的作用下保持静止,所以细线的拉力为F=F浮﹣G=5N﹣4N=1N,故③错误;
④甲、乙两图所示情况,木块和水仍然在容器中,总重力仍等于木块、水、容器的重力之和,总重力不变,对桌面的压力不变,根据p=可知,容器对水平桌面的压强相等,故④正确。
故选:C。
11、D
【分析】(1)根据B的体积和高,可求出底面积,利用p=可求出压强;
(2)根据浮沉条件、阿基米德原理、力的平衡条件求物体的体积和浮力的变化量,再由压强和密度的定义即可求解。
【解答】解:A、B的底面积为:SB===50cm2
如图所示状态,B物体对烧杯底的压强为:pB==2.6×103Pa,故A错误;
B、烧杯漂浮,浮力等于总重力,AB受到的总重力GAB=GA+GB=8N+5N=13N
将A、B放入水中静止后,弹簧与图示状态相比伸长了8cm,弹簧弹力每改变1N,长度改变0.8cm,所以弹力变化了10N;
因为原先弹簧压缩,弹力为8N,所以现在弹簧伸长,弹力为2N;
受力分析可知,A受到浮力为F浮A=2N+8N=10N;
B受到的最大浮力为:F浮B=ρ水gVB=1×103kg/m3×10N/kg×200×10﹣6m3=2N
容器为柱形容器,且原来装有A、B两物体的烧杯处于漂浮状态
则容器底受到水的压力:F1=G水+G烧杯+GAB=G水+G烧杯+13N﹣﹣﹣﹣﹣①
将A、B放入水中静止后,烧杯仍然漂浮,此时容器底受到水的压力:
F2=G水+G烧杯+F浮A+F浮B=G水+G烧杯+12N﹣﹣﹣﹣﹣②
①﹣②可得,水对容器底部的压力减小量为:ΔF=1N
水对容器底部的压强减小量为:,故B错误;
C、将一些水带入烧杯中,与开始相比浮力增大量为带入水重力,根据F浮=ρgV排,V排增大量其实就是带入水的体积,所以水位不变,故C错误;
D、由选项B的解析可知,B受浮力2N,弹力2N,重力5N,所以还受支持力1N,所以一定沉底了,所以A应该完全浸没。
由F浮=ρgV排得正方体A的体积为:
A的密度为:,故D正确;
故选:D。
12、B
【分析】要解决此题,需要掌握二力平衡条件,知道处于平衡状态的物体受平衡力的作用,一对平衡力的大小相等。
B在水中,所以受到水对它的浮力作用,所以B对A的拉力为F=G﹣F浮。
需要对物体A进行受力分析,确定两种情况下所受摩擦力的方向。根据二力平衡的条件列出两种情况下的关系式便可解决。
【解答】解:当用铝块C时,物体A向左匀速运动,所以所受摩擦力方向水平向右。
物体B在水中,受水对它向上的浮力,所以B对A的拉力FB=GB﹣F浮。
根据二力平衡条件:GC=f+GB﹣F浮
B、C是体积相同的实心铝块,所以重力相等。因此f=F浮。
若换为D,物体A向右匀速运动,所以所受摩擦力方向水平向左。
根据二力平衡条件:GD+f=GB﹣F浮,则GD=GB﹣f﹣F浮 又因为f=F浮,所以GD=GB﹣2F浮 即mDg=ρ铝VBg﹣2ρ水VBg
则mD=ρ铝VB﹣2ρ水VB=2.7g/cm3×10cm3﹣2×1g/cm3×10cm3=7g
故选:B。
二、填空题(本题共6小题,每空3分,共18分)
13.大气压;增大
【分析】小鸡自动喂水器主要应用大气压支持瓶内的水柱,当随着自动喂水的装置内水的减少,当瓶口刚露出水面时,会有少量空气进入瓶中,瓶内气压增大,瓶子的水会下降流出一部分,使水位重新升高,瓶口继续没入水中,空气不再进入,如此反复。
【解答】解:当水面刚浸没瓶口,水不再流出时,说明外界大气压等于与瓶内气压和瓶内的水压之和,因此水不再流出是大气压的作用,当瓶口露出水面,瓶内就会进入空气,水就会流出来,瓶内空气加上水的压强等于大气压,由于水的深度变小,由p=ρgh可知液体压强减小,外界大气压不变,所以瓶内气压与原来瓶内的气压相比变大。
故答案为:大气压;增大。
14.2.5×103;2.4×10﹣3
【分析】(1)由图知圆柱体M刚好浸没时下表面在水中的深度,根据p=ρgh求出此时下表面受到的液体压强;
(2)由图可知,圆柱体M下表面未进入水中时弹簧测力计的示数,即圆柱体重力;当h=25cm即圆柱体浸没时,由图可知圆柱体的高和此时弹簧测力计的示数,根据称重法求出圆柱体受到的浮力;根据阿基米德原理求出圆柱体的体积(排开水的体积),根据体积公式求出圆柱体的底面积。
【解答】解:(1)根据题意和图示可知,圆柱体刚好浸没时,圆柱体下表面在水中的深度为:h底=25cm=0.25m;
因此下表面所受液体压强:p=ρ水gh底=1.0×103kg/m3×10N/kg×0.25m=2.5×103Pa;
(2)由图可知,圆柱体M下表面未进入水中时,弹簧测力计的示数等于圆柱体重力,即:G=F=7.2N;
根据题意和图示可知,h底=25cm,圆柱体M刚好全部浸没时,弹簧测力计示数F′=1.2N,则当圆柱体M浸没时,它所受到的浮力为:
F浮=G﹣F′=7.2N﹣1.2N=6N;
由于圆柱体M刚好浸没时,则根据浮力计算公式F浮=ρgV排知物体M的体积为:
V=V排===6×10﹣4m3,
又h=25cm,圆柱体M刚好全部浸没时,圆柱体下表面在水中的深度等于圆柱体的高度,即:h=h底=25cm=0.25m;
根据V=Sh可得,圆柱体M的底面积为:
S===2.4×10﹣3m2。
故答案为:2.5×103;2.4×10﹣3。
15.5:4;4
【分析】(1)根据F=pS可求出甲、乙对地面的压力之比;
(2)在两物体上沿竖直方向截去部分的质量相等后,根据ΔS==,求出截去部分和地面的接触面积,进一步求出ΔS甲:ΔS乙;在两物体上沿竖直方向截去质量相等的部分并分别放在对方剩余部分的上方后,根据Δp=表示出甲、乙对底面的压强增加量,利用Δp甲:Δp乙=2:3和底面积关系得出ΔS甲与S甲的关系,进一步求出甲物体沿竖直方向切去的质量。
【解答】解:(1)甲、乙是放在水平地面上的两个质地均匀的长方体,它们对水平地面的压强相等,底面积之比S甲:S乙=5:4,
根据F=pS可知,甲、乙对地面的压力之比:
F甲:F乙=P甲S甲:P乙S乙=S甲:S乙=5:4;
(2)因为甲、乙是放在水平地面上的两个质地均匀的长方体,因此它们的重力等于它们对水平地面的压力,
所以G甲:G乙=F甲:F乙=5:4;
所以ρ甲:ρ乙=:=:=×=××=××=2:3;
因在两物体上沿竖直方向截去部分的质量相等,根据ΔS==可知:
==×=×=1,即:ΔS甲=ΔS乙;
在两物体上沿竖直方向截去质量相等的部分并分别放在对方剩余部分的上方后,甲、乙对底面的压强增加量分别为:
Δp甲==,Δp乙==
又因Δp甲:Δp乙=2:3,S甲:S乙=5:4
所以,3×=2×=
整理可得:ΔS甲=S甲
则甲物体沿竖直方向截去的质量:
Δm甲=ρ甲ΔV甲=ρ甲ΔS甲h甲=ρ甲×S甲h甲=m甲=×10kg=4kg。
故答案为:5:4;4。
16.22;2.5×103kg/m3;
【分析】(1)甲图中容器对桌面的压力大小就等于物体自身的重力;
(2)根据压强变化可以知道液面的变化,根据液面的变化可以求出ΔV排,ΔV排的大小就等于物体A体积的;
根据物体的漂浮原理可计算出物体A密度;
知道物体A的密度,根据物体A、B用细线相连时,处于悬浮状态,可以计算出物体B的密度。
【解答】解:(1)甲中容器对水平桌面的压力:F=G总=m总g=(m水+m容)g=(2kg+0.2kg)×10N/kg=22N;
(2)根据A物块上浮,最终漂浮,则FA浮=GA;
又因为物块A有体积露出水面可知,ρ水g×VA=ρAgVA;
则ρA=ρ水=×1.0×103kg/m3=0.75×103kg/m3;
根据水对容器底的压强变化了60Pa,根据p=ρgh可知,Δh===6×10﹣3m=0.6cm;
物体A露出水面的体积等于容器中液面下降的体积,即VA=S容Δh;
则物体A的体积:VA=4S容Δh=240cm3;
物体B的体积:VB=VA=40cm3;
物体A受到的重力:GA=ρAVAg=0.75×103kg/m3×240×10﹣6m3×10N/kg=1.8N;
把A、B两物块用细线相连放入水中时,两物块恰好悬浮可知,F浮总=ρ水g(VA+VB)=1.0×103kg/m3×10N/kg×280×10﹣6m3=2.8N;
又因为F浮总=G总=GA+GB可知,GB=F浮总﹣GA=2.8N﹣1.8N=1N;
物体B的密度:ρB====2.5×103kg/m3。
故答案为:22;2.5×103kg/m3;
17. 2×103;23。
【分析】本题比较综合,首先利用丙图获取甲的高度,计算出甲的密度;再利用甲切割10厘米,导致乙对地面的压强变化1000Pa,计算出乙的横截面积。利用水的体积及切割出来的甲的体积,算出乙的水的深度,计算出第一问水对乙容器的压强;假设切割a后利用正柱体压强公式算出甲物体对地面的压强,切割后放入乙中,导致乙压强增加量为切除甲的重力除以乙的横截面积,算出乙容器对地面的压强。利用这两个压强相等算出a的具体值。
【解答】解:由图丙知,甲物体的高度为0.4m,利用p=ρgh,得到ρ甲为2×103kg/m3;
由于甲切除的体积为V甲切=S甲×Δh=1000cm3,甲切除的重力为G甲切=ρ甲gV甲切=20N,利用乙容器对地面的压强变化了2600Pa﹣1600Pa=1000Pa,
∵S乙×1000Pa=20N,∴S乙=200cm2,Δh=10cm时,乙容器中原有的水与切下的甲物体恰填充满整个乙容器,之后水开始溢出,Δh=20cm时,此时切下来的甲物体与容器乙恰等高,因此此时水溢出达到最大,由于原来水的体积为3000cm3,放入20cm的甲物体后,剩余水的体积为V剩=(200cm2﹣100cm2)×20cm=2000m3;得溢出水的体积为ΔV=3000cm3﹣2000cm3=1000cm3;
由于水溢出,从Δh=10cm到Δh=20cm这一段中乙容器对地面产生的压强比原有应减少Δp=ρ水gΔV÷S乙=500Pa
故此时乙容器对底面的压强为p乙′=2600Pa+1000Pa﹣500Pa=3100Pa,
故Δh>20cm时,p乙的解析式为p乙=3100Pa+100(Δh﹣20)Pa﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
同时p甲=8000Pa﹣200Δh Pa﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
两图线的交点表示压强相等,即p甲=p乙
则联立①②两式可解得此时Δh=a=23cm。
故答案为:2×103;23。
18.1000;1:4。
【分析】(1)根据液体计算公式p=ρgh计算即可得出水对乙容器底的压强;
(2)根据公式V=Sh、ρ=求得圆柱体甲的密度;
若将甲水平切去一部分,并缓慢放入乙中,静止时沉底:由V=Sh可得容器中原有水此时的高度,即甲浸入水中的高度;由题意可知当切去的高度为a时,甲剩余部分对桌面的压强与乙容器中水对容器底压强之比为2:1,甲剩余部分对水平桌面的压强可表示为p甲剩=ρ甲gh剩,水对容器底部的压强为p=ρ水gh,综合可得切去的高度,进而算出切去部分体积与圆柱体甲总体积之比。
【解答】解:(1)乙容器内水的深度:h=10cm=0.1m,此时水对乙容器底的压强:
p=ρ水gh=1.0×103kg/m3×10N/kg×0.1m=1000Pa;
(2)圆柱体甲的密度:
ρ甲===0.8g/cm3=0.8×103kg/m3
若将甲水平切去一部分,并缓慢放入乙中,静止时沉底:
容器中水的高度变为:h水===0.2m,则此时甲浸入水中的高度为0.2m
圆柱体甲剩余部分对水平桌面的压强为:p甲剩=ρ甲gh剩=ρ甲g(h总﹣a)×10﹣2m=0.8×103kg/m3×10N/kg×(50﹣a)×10﹣2m=(4000﹣80a) Pa,
水对容器底部的压强:p水=ρ水gh水=1.0×103kg/m3×10N/kg×0.2m=2000Pa,由p甲剩=2p水可得:(4000﹣80a)Pa=4000Pa,故a=0cm;所以此时,故假设不成立。
(3)若将甲水平切去一部分,并缓慢放入乙中,静止时漂浮:
漂浮时物体所受浮力等于物体的重力为:F浮=Ga,即ρ甲gVa=ρ水gVa排,则===,此时甲浸入水中的深度:ha== a;
水面上升的高度为:Δh==;
甲剩余部分对水平桌面的压强:p甲剩=ρ甲gh剩=ρ甲g(h﹣a)×10﹣2m=0.8×103kg/m3×g×(50﹣a)×10﹣2m,水对容器底部的压强:p水=ρ水g(h水+Δh)=1.0×103kg/m3×g×(10+)×10﹣2m,由p甲剩=2p水可得:a=12.5cm,故假设成立。
此时切去部分体积与圆柱体甲总体积之比==12.5cm:50cm=1:4。
故答案为:1000;1:4。
三、解答题(本题共5小题,共46分)
19.(1)2.7;0.3;(2)物体排开液体的体积;a、d、e;无关;(3)1.4×103;(4)300;1.2×10﹣4;2.5×103。
【分析】(1)当物体浸在液体中时,物体所受的浮力等于物体重G减去弹簧测力计的示数F,分别计算出b、c、d浮力大小,得出随着物体浸入液体的体积(排开液体的体积)的增加,物体所受的浮力的变化情况。
(2)根据表格中数据我们可以求得图e中物体所受的浮力,与图d中物体所受浮力作比较。图d、e物体浸没在液体中,排开液体的体积相同,只是所处的深度不同,据此得出物体所受的浮力与所处的深度的关系;
(3)根据表格中数据我们可以求得图f中物体所受的浮力。图e、f两次实验中,物体排开液体的体积相同,所以我们可以根据阿基米德原理F浮=G排=ρ液gV排,列出等式求解出液体的密度;
(4)图A测量烧杯和水的总质量,图C测量烧杯、水和矿石三者的总质量,两次电子秤示数之差即为矿石的质量;B图中,矿石悬挂在细绳上,矿石受到水竖直向上的浮力,物体间力的作用是相互的,矿石给水一个竖直向下的压力作用在容器的底部,导致电子秤的示数增加,对比A图,增加的压力和浮力大小相等;
根据阿基米德原理,利用矿石的浮力求出矿石排开液体的体积,矿石的体积等于矿石排开液体的体积,然后根据密度公式求出矿石的密度。
【解答】解:
(1)由图a可知,弹簧测力计分度值为0.1N,其示数为2.7N,即物体所受的重力为2.7N。
由表可知,图b中弹簧测力计的示数为2.4N,则图b中物体所受的浮力F浮b=2.7N﹣2.4N=0.3N;
(2)同理可求得图c中物体所受的浮力为0.4N,图d中物体所受的浮力为0.5N;比较b、c、d三个图我们可以发现,随着物体浸入液体的体积(排开液体的体积)的增加,物体所受的浮力也在增加,所以我们可以得出结论:物体所受的浮力与其排开液体的体积有关,排开液体的体积越大,受到的浮力就越大;
同理可求得图e中物体所受的浮力为0.5N,与图d中物体所受浮力相等;图d、e中,物体浸没在液体中,排开液体的体积相同,只是所处的深度不同,而物体所受的浮力相同,这说明物体所受的浮力与物体所处的深度无关;
(3)根据表格中数据,图f中物体所受的浮力为F浮f=2.7N﹣2.0N=0.7N。
图e、f两次实验中,物体排开液体的体积相同,所以我们可以根据阿基米德原理列出:=;
代入数值=,可得步骤f中液体的密度为1.4×103kg/m3;
(4)由AC两图可得矿石的质量为:m石=mC﹣mA=650g﹣350g=300g=0.3kg;
B图中,矿石悬挂在细绳上,矿石受到水竖直向上的浮力,物体间力的作用是相互的,矿石给水一个竖直向下的压力作用在容器的底部,导致电子秤的示数增加,对比A图,增加的压力和浮力大小相等,
所以,矿石浸没时受到的浮力F浮=(mB﹣mA)g=(0.470kg﹣0.350kg)×10N/kg=1.2N;
根据阿基米德原理,F浮=ρ水gV排=ρ水gV石=1.0×103kg/m3×10N/kg×V石=1.2N解得V石=1.2×10﹣4m3;
矿石的密度:ρ石===2.5×103kg/m3;ρ石===2.5×103kg/m3。
故答案为:(1)2.7;0.3;(2)物体排开液体的体积;a、d、e;无关;(3)1.4×103;(4)300;1.2×10﹣4;2.5×103。
20.(1)空盒A漂浮在水面上时,盒底部受到水的压强大小为100Pa。
(2)空盒A漂浮在水面上时所受浮力的大小为1N。
(3)小红把金属块B从水中捞起后放进盒A并漂浮在水面上时,盒A受到的浮力的大小为9.75N。
(4)第(3)问中水槽里水位升高3.75cm。
【分析】(1)空盒A漂浮在水面上时,已知盒底浸入水中的深度,根据p=ρgh求出盒底部受到水的压强大小;
(2)根据V排=SAh浸算出空盒A排开水的体积,根据阿基米德原理算出空盒A受到的浮力;
(3)因物体漂浮时受到的浮力和自身的重力相等算出空盒A的重力,根据密度公式算出金属块B的质量,根据G=mg求出金属块B的重力;
把金属块B从水中捞起后放进盒A并漂浮在水面上时,根据物体漂浮条件即可求出此时盒A受到的浮力的大小;
(4)首先求出金属块B在水中时AB排开水的总体积,再根据阿基米德原理的变形公式求出A与B并漂浮在水面上时盒A排开水的体积,并求出排开水的体积的增加量,根据ΔV排=SΔh即可求出水槽里水位变化的高度。
【解答】解:(1)空盒A漂浮在水面上时,盒底浸入水中的深度h浸=1cm=1×10﹣2m,则盒底部受到水的压强:
p=ρ水gh=1.0×103kg/m3×10N/kg×1×10﹣2m=100Pa;
(2)空盒A漂浮在水面上时排开水的体积:V排=SAh浸=100cm2×1cm=100cm3=1×10﹣4m3
空盒A受到的浮力:F浮=ρ水gV排=1×103kg/m3×10N/kg×1×10﹣4m3=1N;
(3)因空盒A漂浮时受到的浮力和自身的重力相等,所以,空盒A的重力:GA=F浮=1N;
根据ρ=可得金属块B的质量:
mB=ρBVB=7.0×103kg/m3×1.25×10﹣4m3=0.875kg
则金属块B的重力:GB=mBg=0.875kg×10N/kg=8.75N
把金属块B从水中捞起后放进盒A并漂浮在水面上时,因物体漂浮时受到的浮力和自身的重力相等,
所以,此时盒A受到的浮力:F浮′=G总=GA+GB=1N+8.75N=9.75N;
(4)金属块B在水中时,AB排开水的总体积为:
V排总=V排+VB=1×10﹣4m3+1.25×10﹣4m3=2.25×10﹣4m3,金属块B从水中捞起后放进盒A,A与B漂浮在水面上时,根据F浮=ρ水gV排可得盒A排开水的体积:
V排′===9.75×10﹣4m3>2.25×10﹣4m3
即:V排′>V排总,所以,金属块B从水中捞起后放进盒A并漂浮在水面上后,水面会升高,排开水的体积的增加量:ΔV排=V排′﹣V排总=9.75×10﹣4m3﹣2.25×10﹣4m3=7.5×10﹣4m3=750cm3,则水槽里水位升高的高度:Δh===3.75cm。
答:(1)空盒A漂浮在水面上时,盒底部受到水的压强大小为100Pa。
(2)空盒A漂浮在水面上时所受浮力的大小为1N。
(3)小红把金属块B从水中捞起后放进盒A并漂浮在水面上时,盒A受到的浮力的大小为9.75N。
(4)第(3)问中水槽里水位升高3.75cm。
21.(1)木块未放入水中时,容器B中的水对容器B底部的压强为2000Pa;
(2)把一个木块缓慢放入容器B中,当木块最终静止时,溢出的水的体积为5×10﹣4m3;
(3)把n个木块缓慢放入容器B中,然后全部取出,容器B能够在A中浮起时,n的最小值为3。
【分析】(1)已知木块未放入水中时,容器B中水的深度,根据p=ρgh求水对容器B底部的压强;
(2)根据ρ=求出木块的质量,根据G=mg求木块的重力,比较木块和水的密度判断木块在水中静止时的状态,根据漂浮条件求出木块受到的浮力,根据阿基米德原理求出木块排开水的体积;
(3)当B刚好漂浮时,B所受的浮力等于剩余水和容器B的总重力,再结合阿基米德原理求得浮力,即可求出需要从B中溢出水的质量,根据漂浮条件求出木块的总重力,进而求出木块的个数。
【解答】解:
(1)木块未放入水中时,容器B中水对容器B底部的压强:
pB=ρ水ghB=1.0×103kg/m3×10N/kg×20×0.01m=2000Pa;
(2)木块的体积:V木=(10cm)3=1000cm3,由ρ=可知,木块的质量:m木=ρ木V木=0.5g/cm3×1000cm3=500g=0.5kg,木块的重力:G木=m木g=0.5kg×10N/kg=5N,若不考虑木块吸水,因为木块的密度小于水的密度,所以木块在水中最终漂浮,由物体的漂浮条件可知,木块受到的浮力:F浮=G木=5N,
由F浮=ρ水gV排可知,此时溢出水的体积为:
V溢=V排===5×10﹣4m3;
由题知,每个木块放入容器B后会立即吸水100g,吸收水的体积V吸===1×10﹣4m3,吸收水的重力G吸=m吸g=0.1kg×10N/kg=1N,吸水后木块的平均密度小于水的密度,所以木块在水中最终还是漂浮,由物体的漂浮条件可知,木块受到的浮力:F浮′=G木+G吸=5N+1N=6N,
由F浮=ρ水gV排可知,此时排开水的体积为:
V排′===6×10﹣4m3;
木块吸水后会导致水面下降,而排开水的体积增大会使得水面升高,且V排′﹣V排=V吸=1×10﹣4m3,所以可知木块吸水对溢出水的体积无影响,则溢出水的体积仍然为5×10﹣4m3;
(3)容器B中装满水时水的体积:VB=SBhB=200cm2×20cm=4000cm3,由ρ=可知,容器B中装满水时水的质量为:m水=ρ水VB=ρ水SBhB=1.0g/cm3×200cm2×20cm=4000g;
把n个木块缓慢放入容器B中,然后全部取出,则木块吸收水的总质量为m吸总=100n(g),设溢出到A容器中水的质量为m(单位为g),结合密度公式可知在容器A中水的体积为:
hA(SA﹣SB)=,则hA===cm
当容器B刚好漂浮时,B容器排开水的体积:
V排′=hASB=cm×200cm2=2m(cm3),B容器排开水的质量:m排′=ρ水V排′=1.0g/cm3×2m(cm3)=2m(单位为g),由物体的漂浮条件和阿基米德原理可知,m排′g=(mB+m水﹣100n﹣m)g,所以2m=mB+m水﹣100n﹣m=800+4000﹣100n﹣m,整理可得3m=4800﹣100n﹣﹣﹣﹣﹣﹣﹣﹣﹣①;
由(2)可知,木块吸水对溢出水的体积无影响,则每个木块溢出水的体积为5×10﹣4m3=500cm3,则n个木块溢出水的总体积V溢总=500n(cm3),所以溢出到A容器中水的质量为m=ρ水V溢总=1.0g/cm3×500n(cm3)=500n(单位为g)﹣﹣﹣﹣②
联立①②解得n=3,即需要木块的个数为3个。
答:(1)木块未放入水中时,容器B中的水对容器B底部的压强为2000Pa;
(2)把一个木块缓慢放入容器B中,当木块最终静止时,溢出的水的体积为5×10﹣4m3;
(3)把n个木块缓慢放入容器B中,然后全部取出,容器B能够在A中浮起时,n的最小值为3。
22.
(1)图甲中,水对容器底的压强是2000Pa;
(2)木球的重力是1N;
(3)图乙中,容器底对塑料球的支持力是0.25N。
【分析】(1)图甲中,知道水深和水的密度,利用p=ρgh求水对容器底的压强;
(2)由题知,当把细绳剪断后,静止时木球露出水面的体积是它自身体积的,利用F浮=G求木球的密度,利用G=mg=ρVg求木球重力;
(3)在图甲中,求出两球排开水的体积,由于木球和塑料球漂浮,受到的总浮力等于两球总重力,据此求塑料球的重力,利用阿基米德原理求塑料球在水中受到的浮力;图乙中,容器底对塑料球的支持力等于塑料球的重力减去浮力。
【解答】解:
(1)图甲中,水对容器底的压强:
p=ρ水gh=1×103kg/m3×10N/kg×0.2m=2000Pa;
(2)由题知,当把细绳剪断后,静止时木球露出水面的体积是它自身体积的,即V排=V木,
因为F浮=G,即ρ水V排g=ρ木Vg,ρ水Vg=ρ木V木g,所以ρ木=ρ水=×1×103kg/m3=0.5×103kg/m3,
木球重力:
G木=m木g=ρ木V木g=0.5×103kg/m3×10N/kg×200×10﹣6m3=1N;
(3)图甲中,两球排开水的体积V排′=(1﹣)V木+V塑=×200×10﹣6m3+25×10﹣6m3=150×10﹣6m3=1.5×10﹣4m3=150cm3,因为木球和塑料球漂浮,所以F浮′=G木+G塑,ρ水V排′g=1N+G塑
1×103kg/m3×10N/kg×1.5×10﹣4m3=1N+G塑,
则塑料球的重力:
G塑=0.5N
塑料球在水中受到的浮力:
F浮塑=ρ水V排塑g=1×103kg/m3×10N/kg×25×10﹣6m3=0.25N
图乙中,容器底对塑料球的支持力:
F支=G塑﹣F浮塑=0.5N﹣0.25N=0.25N;
答:(1)图甲中,水对容器底的压强是2000Pa;
(2)木球的重力是1N;
(3)图乙中,容器底对塑料球的支持力是0.25N。
23.见试题解答内容
【分析】(1)因为密度计是一根两端封闭即空心的,所以能使密度计浮在液体表面,为了使它保持竖直的漂浮,就在管的底部封存少许铅粒;
(2)密度计的质量一定,在液体中受力平衡,受到的浮力总是等于重力,被测液体的密度越大,排开液体的体积越小,浸入液体部分也越小,据此分析回答;
(3)根据密度计的刻度由上至下数值逐渐增大分析;
(4)为了使测量结果更准确,使密度计上两条刻度线(如0.9、1.0)之间的距离大一些,因为ΔV=sh,所以可知减小S,即可使h变大,据此设计即可。
【解答】解:
(1)为了让饮料吸管能竖直的漂浮在液体中,吸管下端塞入一些铜丝作为配重,这样做目的是让密度计竖直漂浮在液体中;若将它放入液体中后不能竖直漂浮,则可以用小钢珠作为配重;
(2)密度计是漂浮在液体中,所受浮力等于本身的重力,保持不变,如果液体的密度越大,则密度计浸入液体中的体积越小,即越往上浮,则露出液面部分的长度越长;所以密度计的刻度是越往下值越大;
(3)因为密度计是漂浮在液体中,所受浮力等于本身的重力,则F浮水=F浮液=G,即ρ水gSH=ρ液gSh=G
∵h=H,h和ρ液是反比例函数
∴刻度分布不均匀。且密度计的刻度由上至下数值逐渐增大;则密度变大时h液变化越小,故C正确;
(4)∵F浮液=G,即ρ液gSh=G,则ΔV=sh
∴ΔV变大,或使h变大,具体做法是:可适当增大配重,用更细的吸管。
故答案为:(1)下端;可以用小钢珠作为配重(重心比铜丝低的材料都可以);
(2)不变;越长;
(3)h=H;C;
(4)增大;用更细的吸管;
