矩形的性质
图片预览



文档简介
课件15张PPT。矩形的性质两组对边
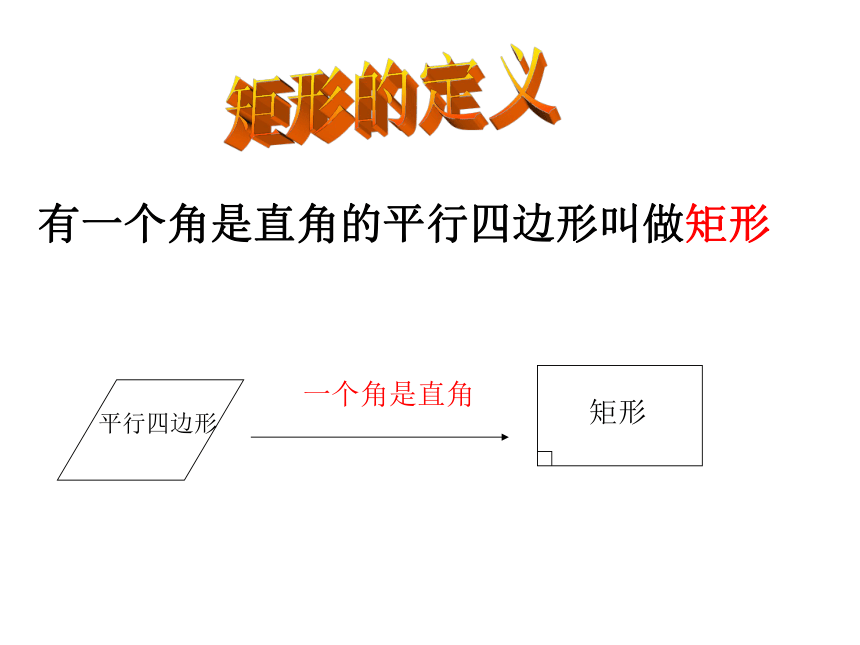
分别平行一个角是
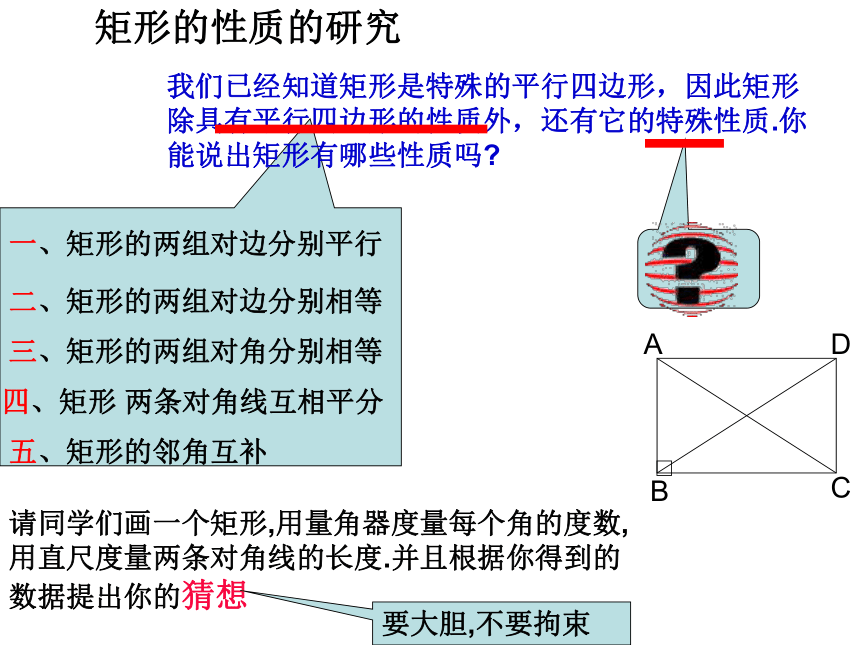
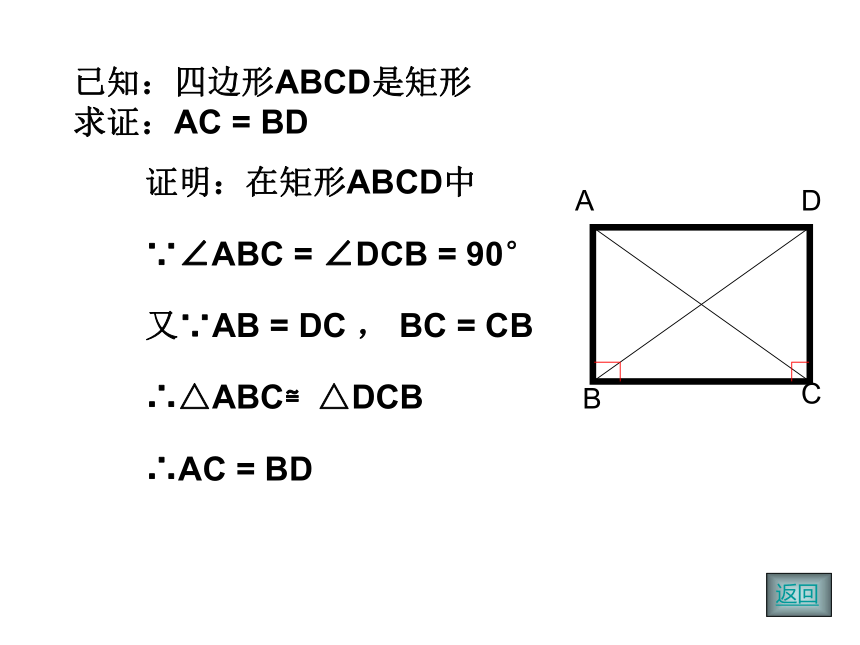
直角矩形情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也,这堂课我们就来研究一种恃殊的平行四边形—— 矩形一个角是直角有一个角是直角的平行四边形叫做矩形矩形的定义矩形的性质的研究我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?E 。四、矩形 两条对角线互相平分三、矩形的两组对角分别相等二、矩形的两组对边分别相等一、矩形的两组对边分别平行五、矩形的邻角互补请同学们画一个矩形,用量角器度量每个角的度数,用直尺度量两条对角线的长度.并且根据你得到的数据提出你的猜想要大胆,不要拘束已知:四边形ABCD是矩形
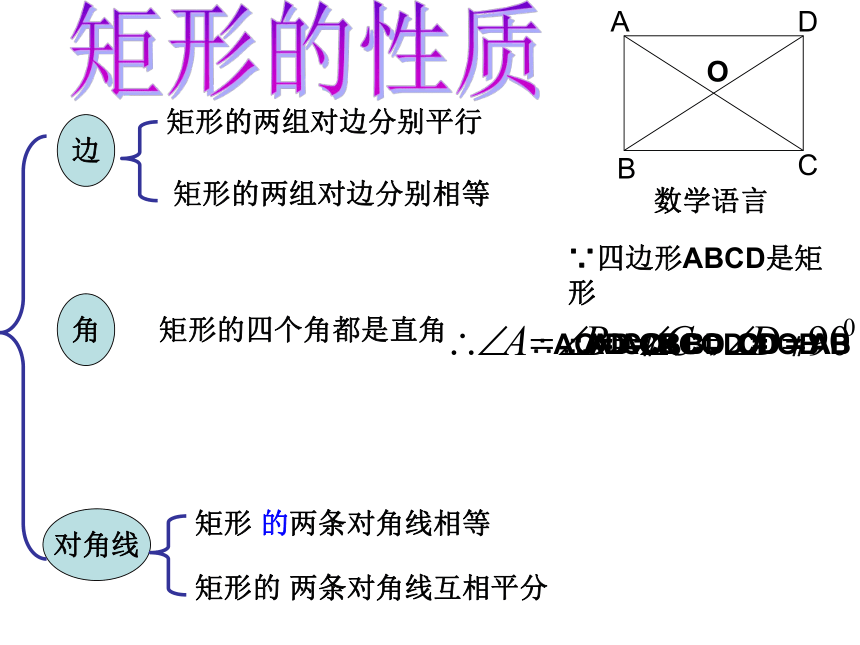
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD矩形的特殊性质矩形的对角线相等数学语言∵四边形ABCD是矩形 ∴AC = BD矩形的 两条对角线互相平分矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形 的两条对角线相等边对角线角数学语言∵四边形ABCD是矩形∴AD = BC ,CD = AB∴AD ∥BC ,CD ∥AB∴AC= BD ∴AO= CO ,OD = OB矩形的性质推论:直角三角形斜边上的中线等于斜边的一半. 如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系已知:在△ABC中∠ACB=90°,AD = BD证明:延长CD到E使DE=CD,连 结AE、BE.∵AD = BD ,CD = EDE∴ACBE是平行四边形又∵∠ACB = 90∴CE = AB由于CD= CE
∴ CD = AB求证:CD = AB例1 已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AB = 4cm.
求矩形对角线的长∴BD = 2AB=2×4=8cm解:∵四边形ABCD是矩形∴OA = OD( )∵ ∠AOD=120°∴ ∠1=30°又∵ ∠ABC=90°( )矩形的对角线相等且平分矩形的每个内角都是直角例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?在矩形ABCD中,有AD=BC;AB=CD;AC=DB;
AO=OC=OB=OD∴AD+BC+AB+DC+2AC+2BD=86又∵AC=DB=13∴AD+AB+BC+DC=86-52=34(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等(C)对边平行且相等(D)对角线相等 (2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等(C)是轴对称图形(D)对角线垂直
(3)由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度
DDB课堂练习 4. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是 课堂练习A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形5. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为 A.50° B.60° C.70° D.80°6. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于 A.30° B.45° C.60° D.120°[ ][ ][ ]DDA如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,
AO= cm,BO= cm. 52.5 2.5本课小结矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 推 论 直角三角形斜边上的中线等于斜边的一半.
分别平行一个角是
直角矩形情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也,这堂课我们就来研究一种恃殊的平行四边形—— 矩形一个角是直角有一个角是直角的平行四边形叫做矩形矩形的定义矩形的性质的研究我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?E 。四、矩形 两条对角线互相平分三、矩形的两组对角分别相等二、矩形的两组对边分别相等一、矩形的两组对边分别平行五、矩形的邻角互补请同学们画一个矩形,用量角器度量每个角的度数,用直尺度量两条对角线的长度.并且根据你得到的数据提出你的猜想要大胆,不要拘束已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD矩形的特殊性质矩形的对角线相等数学语言∵四边形ABCD是矩形 ∴AC = BD矩形的 两条对角线互相平分矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形 的两条对角线相等边对角线角数学语言∵四边形ABCD是矩形∴AD = BC ,CD = AB∴AD ∥BC ,CD ∥AB∴AC= BD ∴AO= CO ,OD = OB矩形的性质推论:直角三角形斜边上的中线等于斜边的一半. 如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系已知:在△ABC中∠ACB=90°,AD = BD证明:延长CD到E使DE=CD,连 结AE、BE.∵AD = BD ,CD = EDE∴ACBE是平行四边形又∵∠ACB = 90∴CE = AB由于CD= CE
∴ CD = AB求证:CD = AB例1 已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AB = 4cm.
求矩形对角线的长∴BD = 2AB=2×4=8cm解:∵四边形ABCD是矩形∴OA = OD( )∵ ∠AOD=120°∴ ∠1=30°又∵ ∠ABC=90°( )矩形的对角线相等且平分矩形的每个内角都是直角例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?在矩形ABCD中,有AD=BC;AB=CD;AC=DB;
AO=OC=OB=OD∴AD+BC+AB+DC+2AC+2BD=86又∵AC=DB=13∴AD+AB+BC+DC=86-52=34(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等(C)对边平行且相等(D)对角线相等 (2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等(C)是轴对称图形(D)对角线垂直
(3)由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度
DDB课堂练习 4. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是 课堂练习A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形5. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为 A.50° B.60° C.70° D.80°6. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于 A.30° B.45° C.60° D.120°[ ][ ][ ]DDA如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,
AO= cm,BO= cm. 52.5 2.5本课小结矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 推 论 直角三角形斜边上的中线等于斜边的一半.
