多边形的外角和
图片预览




文档简介
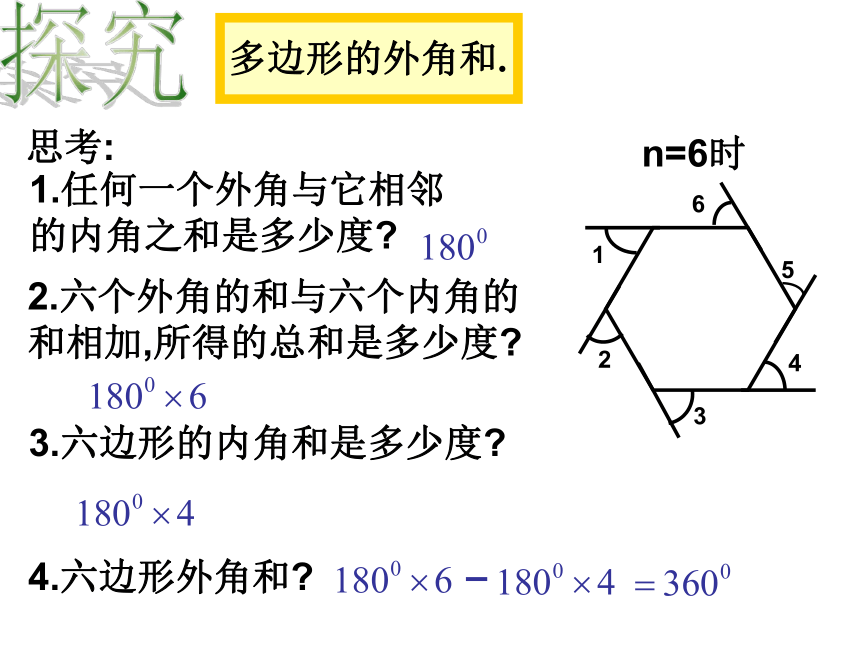
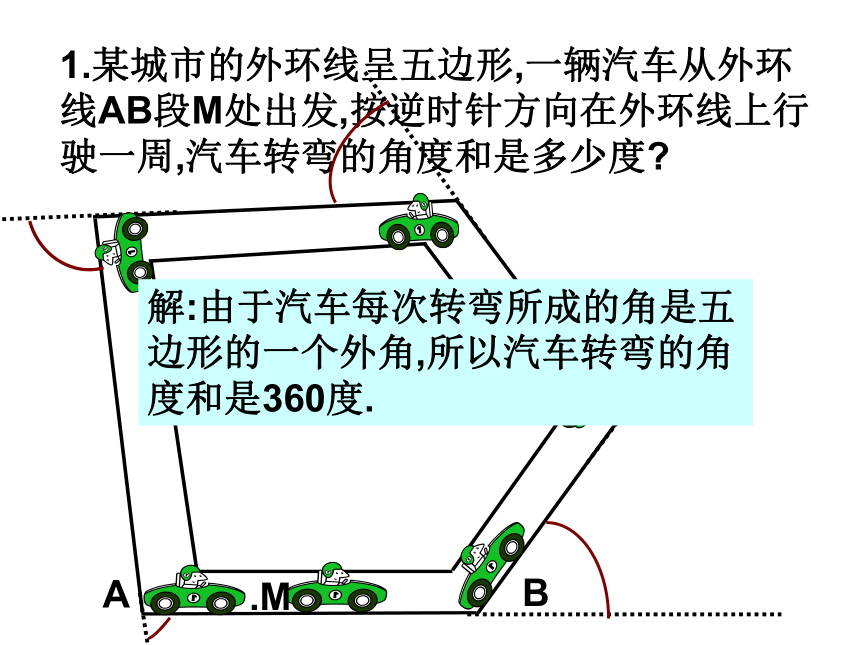
课件15张PPT。多边形的外角和探究多边形的外角和.3.六边形的内角和是多少度?思考:n=6时4.六边形外角和? – 1.任何一个外角与它相邻的内角之和是多少度?2.六个外角的和与六个内角的和相加,所得的总和是多少度?多边形的外角和等于360度探究多边形的外角和.5.n 边形外角和是多少?n个内角与n个外角和n个内角和_=n个外角和_1.某城市的外环线呈五边形,一辆汽车从外环线AB段M处出发,按逆时针方向在外环线上行驶一周,汽车转弯的角度和是多少度?.M解:由于汽车每次转弯所成的角是五边形的一个外角,所以汽车转弯的角度和是360度.AB2.一个多边形的每个内角都是1080,
问这个多边形是几边形?
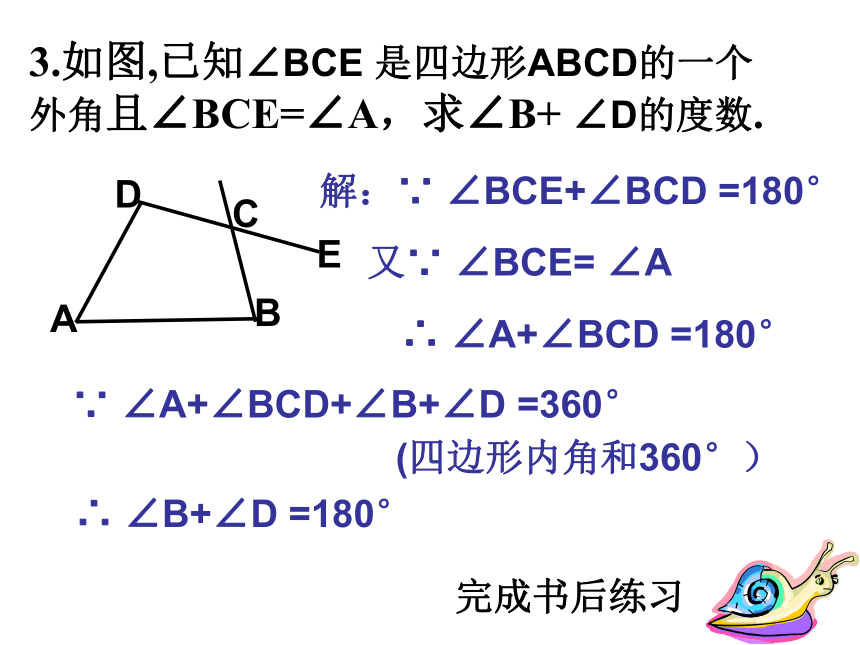
解:设多边形的边数为n,由题意得:解得:n=5答:这个多边形是五边形180(n – 2)= 108n360÷(180 –108)= 5答:这个多边形是五边形解二:3.如图,已知∠BCE 是四边形ABCD的一个外角且∠BCE=∠A,求∠B+ ∠D的度数.ABCDE完成书后练习解:∵ ∠BCE+∠BCD =180°又∵ ∠BCE= ∠A∴ ∠A+∠BCD =180°∵ ∠A+∠BCD+∠B+∠D =360°(四边形内角和360°)∴ ∠B+∠D =180°[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,
所以:(n-2)·180=3×360
解得:n=8
答:这个多边形是八边形. 例题赏析1.若一个凸多边形的内角和等于它的外角和,则它的边数是_______.
2.如果一个多边形的每一个外角都相等,并且它的内角和为2880°,那么它的内角为_________.
3.一个多边形的每个外角都是12°,则这个多边形是_______边形.
4.正n边形的一个内角为120°,那么n为( ) A.5 B.6 C.7 D.8 自测题:416030B课外拓展1.一个多边形内角和与外角和度数之比为9:2,求这个多边形的边数解:设这个多边形的边数为n由题意得:180(n – 2):360 = 9 :2n – 2 = 9n = 11答:这个多边形是十一边形。课外拓展2一个多边形中,最多有几个内角为锐角?解:∵多边形的外角和是360°∴多边形的外角中最多有三个钝角∴多边形的内角最多有三个锐角3.一个多边形除一个内角外,其余各个内角和为16800,求这个多边形的边数及被去掉的这个内角的度数?课外拓展解:设去掉的内角的度数为x°
这个多边形的边数为n则 1680 < 180(n – 2)<1680+180 ∴ x = 180×(12 – 2)– 1680 = 120 ∵n为整数,∴n = 12答:这个多边形为十二边形,去掉的内角的度数为120°4. 如图,求FABCDEG解:∵ ∠A+∠B+∠C+∠1 =360°又∵ ∠D+∠E+∠2=180°(四边形内角和360°)∠A+∠B+∠C+ ∠D+ ∠E+ ∠F+ ∠G =540°123∠E+∠F+∠G+∠3 =360°∠1+∠2+∠3+∠E =360°(三角形内角和180°)①+ ② +④-③得①②③④5. 一个多边形每个内角为135度,
求它的对角线的条数?6.一个凸n边形的内角和小于2008度,
求n的最大值解:360÷(180 – 135) = 88 ×(8 – 3)÷ 2 = 20解:180(n – 2)< 2008答:它的对角线的条数有20条答:n的最大值为13.
小结1多边形的外角和如何证明?2多边形的研究方法:演绎推理;归纳推理。3.多边形的外角最多有几个钝角?回家作业:1、校内完成练习册22.1(2)节作业。2、一课一练22.1(2)3、预习22.2(1)节(书P71—P72),
完成P72书上练习22.2(1)。
问这个多边形是几边形?
解:设多边形的边数为n,由题意得:解得:n=5答:这个多边形是五边形180(n – 2)= 108n360÷(180 –108)= 5答:这个多边形是五边形解二:3.如图,已知∠BCE 是四边形ABCD的一个外角且∠BCE=∠A,求∠B+ ∠D的度数.ABCDE完成书后练习解:∵ ∠BCE+∠BCD =180°又∵ ∠BCE= ∠A∴ ∠A+∠BCD =180°∵ ∠A+∠BCD+∠B+∠D =360°(四边形内角和360°)∴ ∠B+∠D =180°[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,
所以:(n-2)·180=3×360
解得:n=8
答:这个多边形是八边形. 例题赏析1.若一个凸多边形的内角和等于它的外角和,则它的边数是_______.
2.如果一个多边形的每一个外角都相等,并且它的内角和为2880°,那么它的内角为_________.
3.一个多边形的每个外角都是12°,则这个多边形是_______边形.
4.正n边形的一个内角为120°,那么n为( ) A.5 B.6 C.7 D.8 自测题:416030B课外拓展1.一个多边形内角和与外角和度数之比为9:2,求这个多边形的边数解:设这个多边形的边数为n由题意得:180(n – 2):360 = 9 :2n – 2 = 9n = 11答:这个多边形是十一边形。课外拓展2一个多边形中,最多有几个内角为锐角?解:∵多边形的外角和是360°∴多边形的外角中最多有三个钝角∴多边形的内角最多有三个锐角3.一个多边形除一个内角外,其余各个内角和为16800,求这个多边形的边数及被去掉的这个内角的度数?课外拓展解:设去掉的内角的度数为x°
这个多边形的边数为n则 1680 < 180(n – 2)<1680+180 ∴ x = 180×(12 – 2)– 1680 = 120 ∵n为整数,∴n = 12答:这个多边形为十二边形,去掉的内角的度数为120°4. 如图,求FABCDEG解:∵ ∠A+∠B+∠C+∠1 =360°又∵ ∠D+∠E+∠2=180°(四边形内角和360°)∠A+∠B+∠C+ ∠D+ ∠E+ ∠F+ ∠G =540°123∠E+∠F+∠G+∠3 =360°∠1+∠2+∠3+∠E =360°(三角形内角和180°)①+ ② +④-③得①②③④5. 一个多边形每个内角为135度,
求它的对角线的条数?6.一个凸n边形的内角和小于2008度,
求n的最大值解:360÷(180 – 135) = 88 ×(8 – 3)÷ 2 = 20解:180(n – 2)< 2008答:它的对角线的条数有20条答:n的最大值为13.
小结1多边形的外角和如何证明?2多边形的研究方法:演绎推理;归纳推理。3.多边形的外角最多有几个钝角?回家作业:1、校内完成练习册22.1(2)节作业。2、一课一练22.1(2)3、预习22.2(1)节(书P71—P72),
完成P72书上练习22.2(1)。
